水泥砂漿抗彈性能研究

苗春賀，陳麗娜，單俊芳，王鵬飛，徐松林,2

（1. 中國科學技術大學，中國科學院材料力學行為和設計重點實驗室，安徽 合肥 230027；2. 中國地震局地震預測研究所高壓物理與地震科技聯合實驗室，北京 100036）

混凝土結構在爆炸作用下一般處于復雜的應力狀態。混凝土材料具有復雜的細觀結構，是一種典型的結構材料，表現出強烈的應變率相關和加載路徑相關特性[1-3]。這使得應力狀態和沖擊速度對此類材料的開坑與破壞行為產生非常重要的影響，相關研究對揭示混凝土結構的防護機理具有重要的參考意義。為了簡化問題，本研究將討論應力狀態對水泥砂漿抗彈性能的影響，主要集中于侵徹阻力和開坑深度兩方面。

目前，有很多關于彈丸侵徹混凝土靶體過程中侵徹阻力和開坑深度的研究[4-6]，相關理論和數值分析的綜述文獻很充分[7-9]。然而，關于應力狀態影響的研究工作并不多，并且主要通過圓形或多邊形鋼管對混凝土等靶材進行約束來實現[10-11]。例如：甄明等[12]開展了12.7 mm 卵形彈侵徹圓形鋼管（外徑140 mm，厚度3.5 mm）約束的混凝土靶體實驗，結果表明約束后靶體的抗彈性能明顯提高；蒙朝美等[13]研究了不同形狀鋼管對靶體抗侵徹能力和靶體破壞模式的影響。鋼管這類約束確實改變了靶體在侵徹過程中的應力狀態，并且隨著侵徹過程的進行，鋼管的約束作用逐漸增強，防護性能得到很大的提升。但是，靶體的初始狀態和侵徹過程中約束體的狀態是未知的，能否真實反映實際侵徹過程不是很好評估；同時，在初始開坑階段，靶體變形較小，鋼管的約束作用很難發揮出來。因此，這類約束可以增強靶體的抗侵徹能力，但無法進行靶體在應力狀態下的抗彈性能研究。本工作將基于新研制的真三軸應力狀態下混凝土侵徹實驗裝置[14]，在前期水泥砂漿侵徹性能初步研究[15]的基礎上，結合數值分析方法，討論應力狀態對水泥砂漿抗彈性能的影響。

1 實驗裝置與數值分析模型

1.1 真三軸靜載下侵徹實驗裝置

本實驗采用邊長為50 mm 的立方體試件。實驗裝置實物如圖1 所示。該實驗系統包括兩部分：一部分是真三軸靜載施加系統，分別由3 個方向的液壓缸（4、8、11）和對應的反力支架組成，可對立方體試件施加三向不等的壓應力；另一部分是彈丸發射和信號測試系統，主要由侵徹方向（y 方向）的高壓氣炮（1）、子彈入射的中空方桿（2）、支撐方桿（3）、水平x 方向（垂直于侵徹方向）的左支撐方桿（6）和右支撐方桿（7），以及z 方向的下左支撐方桿（9）和上左支撐方桿（10）等組成。

圖1 真三軸靜載混凝土侵徹實驗裝置Fig. 1 Experimental device of concrete specimen under true tri-axial confinement

實驗的第1 階段：在立方體試件的3 個方向分別施加預定的靜載 σx、 σy和 σz。實驗的第2 階段：y 方向的高壓氣體驅動子彈，從y 方向中空方桿中的彈道加速射出，撞擊試件。記錄子彈速度和6 根桿上的波動信號，由此可得到侵徹過程中立方體試件6 個面的動態響應。實驗結束后，對靶體的開坑深度等破壞情況進行拍攝和測量，采用三維光學掃描儀對侵徹實驗的試件進行三維掃描成像，評估侵徹效 果。水泥砂漿和混凝土的實驗結果參見文獻[14-15]。

1.2 數值分析

真三軸靜載侵徹實驗系統的數值模型如圖2所示，其中：6 根方桿的截面尺寸均為50 mm × 50 mm，x、y、z 方向各有兩根長度相同的桿，桿長分別為2.0、1.5、1.0 m；y 方向的入射桿中心有直徑為6 mm的彈道。

圖2 有限元計算模型Fig. 2 Finite element model

采用30CrMnSi 合金結構鋼平頭彈，其直徑為5 mm，長度為20 mm。靶體材料為M10 水泥砂漿，采用S 型砂漿的HJC 本構模型[16]描述，具體參數如表1 所示，其中： ρ0為 密度， G為剪切模量，AHJC為特征化黏性強度系數，BHJC表示特征化壓力硬化指數，CHJC為應變率影響參數，NHJC為壓力硬 化指 數， f′為 單軸 抗 壓強 度，T 為 拉伸 強 度， ε˙0為參 考 應變 率， εf,min為 材料 斷 裂時 的 最小 塑 性應 變，Smax為最大特征化等效應力，pc為壓垮時的靜水壓力， μc為 壓垮時的體積應變， pl為彈性極限下的靜水壓力， μl為彈性極限下的體積應變，k1、k2、k3為壓力常數，D1、D2為損傷常數。彈丸材料采用JC 本構模型[17]描述，具體參數見表2，其中： T0為參考溫度，c 為材料比熱容，AJC為材料在室溫條件下的靜態屈服強度，BJC為材料應變硬化模量，nJC為應變硬化指數，CJC為應變率常數，Tm為材料熔點，d1、d2、d3、d4、d5均為材料失效參數。6 根方形鋼桿采用線彈性模型描述，密度為7 850 kg/m3，彈性模量E = 210 GPa，泊 松比 μ = 0.3。

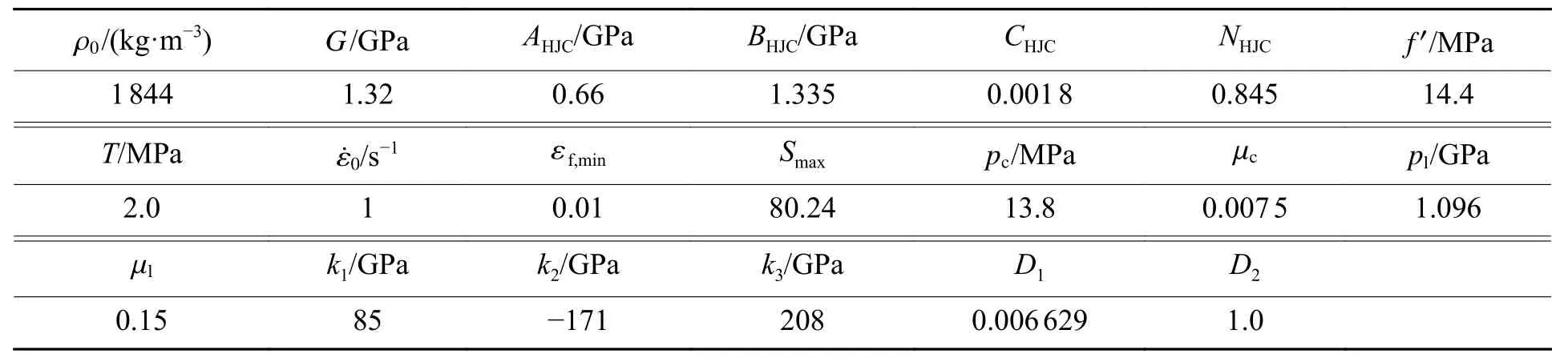
表1 水泥砂漿的HJC 本構模型參數Table 1 Parameters of HJC model for cement mortar

表2 彈丸JC 本構模型參數Table 2 Parameters of JC model of projectile

2 水泥砂漿中的開坑深度

2.1 主要經驗公式

（1）ACE 公式

ACE 公式是由美國陸軍工程兵提出的混凝土侵徹深度經驗公式，表達式為[18]

式中：X 為彈體侵徹深度(m)，D 為彈丸的口徑密度(kg/m3)，d 為彈丸直徑(m)，fc為混凝土靶的無側限抗壓強度(Pa)，v0為彈丸初始速度(m/s)。

（2）修正NDRC 公式

美國國防委員會提出了剛性彈體侵徹理論，并在此基礎上，通過分析大量實驗數據，提出適用于動能彈侵徹混凝土靶的半經驗公式[19]

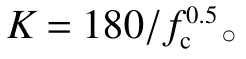
式中： M為彈丸的質量(kg)，fc的單位為Pa。

（3）Barr 公式

Barr[21]針對低速實驗結果，對NDRC 公式進行了修正，公式如下

（4）Young 公式

美國Sandia 國家實驗室提出了預測天然土材料和混凝土侵徹的經驗公式，通常稱為Young 公式[22]，其形式如下

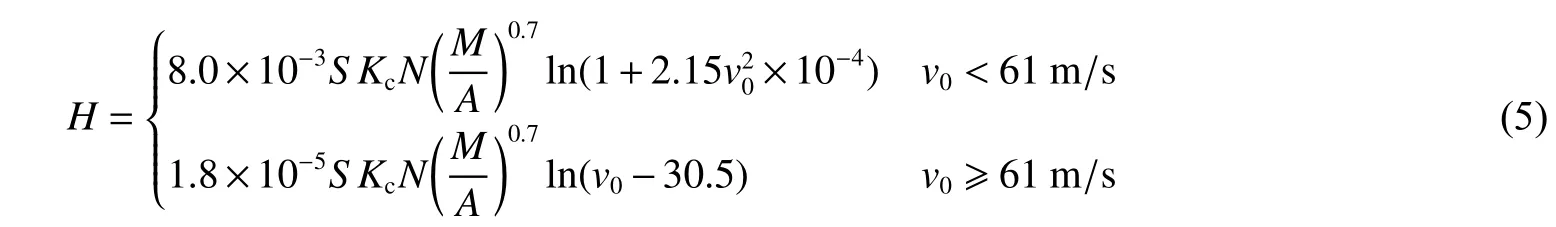
式中：M 的單位為kg；Kc為縮尺效應，當M ＜ 182 kg 時，Kc= 0.46M0.15，當M ≥ 182 kg 時，Kc= 1；A 為彈丸的最大橫截面積(m2)；S 為阻力參數。對于巖石， S =2.7(fc/Q)－0.3，Q 為巖石質量指標，對于混凝土，S =0.085KetcTc(11－P)(35/fc)0.3， 其中：fc的單位為MPa； Ke=(F/Wl)0.3，Wl為靶體寬度與彈體直徑之比，對于鋼筋混凝土，F = 20，對于素混凝土，F = 30，如果Wl＞ F，取Ke= 1；P 為混凝土體積配筋率；tc為混凝土澆筑時間，以年為單位，若澆筑滿一年，則取tc= 1；Tc為靶體厚度h 與彈體直徑d 的比值，在0.5～6 之間，在缺少數據無法計算的情況下，可取0.9。

（5）UMIST 公式

Reid 等[23]對大量混凝土沖擊試驗進行了分析和總結，考慮了應變率效應對混凝土強度的影響，提出了預測彈丸低速侵徹鋼筋混凝土靶板的侵徹深度公式，即

式中： σt為混凝土的動態強度(Pa)， σt=4.2 fc+135.0+(0.014fc+0.450)v0，其中fc的單位為MPa。對于平頭彈，N = 0.72；對于球頭彈，N = 0.84；對于鈍頭彈，N = 1.00；對于尖卵形彈，N = 1.14。

（6）Chen 和Li 的無量綱侵徹深度公式

Chen 和Li[5,24]引入了兩個無量綱量，即撞擊函數I 和彈頭形狀函數N，將Forrestal 半經驗公式無量綱化，并應用滑移場理論將公式的適用性推廣到淺層和中等深度的侵徹，提出開坑深度與彈頭形狀的關系。無量綱侵徹深度公式如下

2.2 開坑深度對比

彈體為平頭實心彈，質量為3.08 g，直徑為5 mm，長度為20 mm。靶體為邊長50 mm 的立方體，平均密度為1 844 kg/m3，無側限抗壓強度fc為14.4 MPa。采用上述經驗公式進行計算，與實驗測試結果和有限元分析結果進行對比，如圖3 所示，圖3 中方括號內的橫線表示自由面，0 表示施加側限。整體上看，隨著沖擊速度的增大，無量綱深度基本單調增大；6 種經驗公式的計算結果存在較大差異，與實驗結果的吻合程度各不相同。

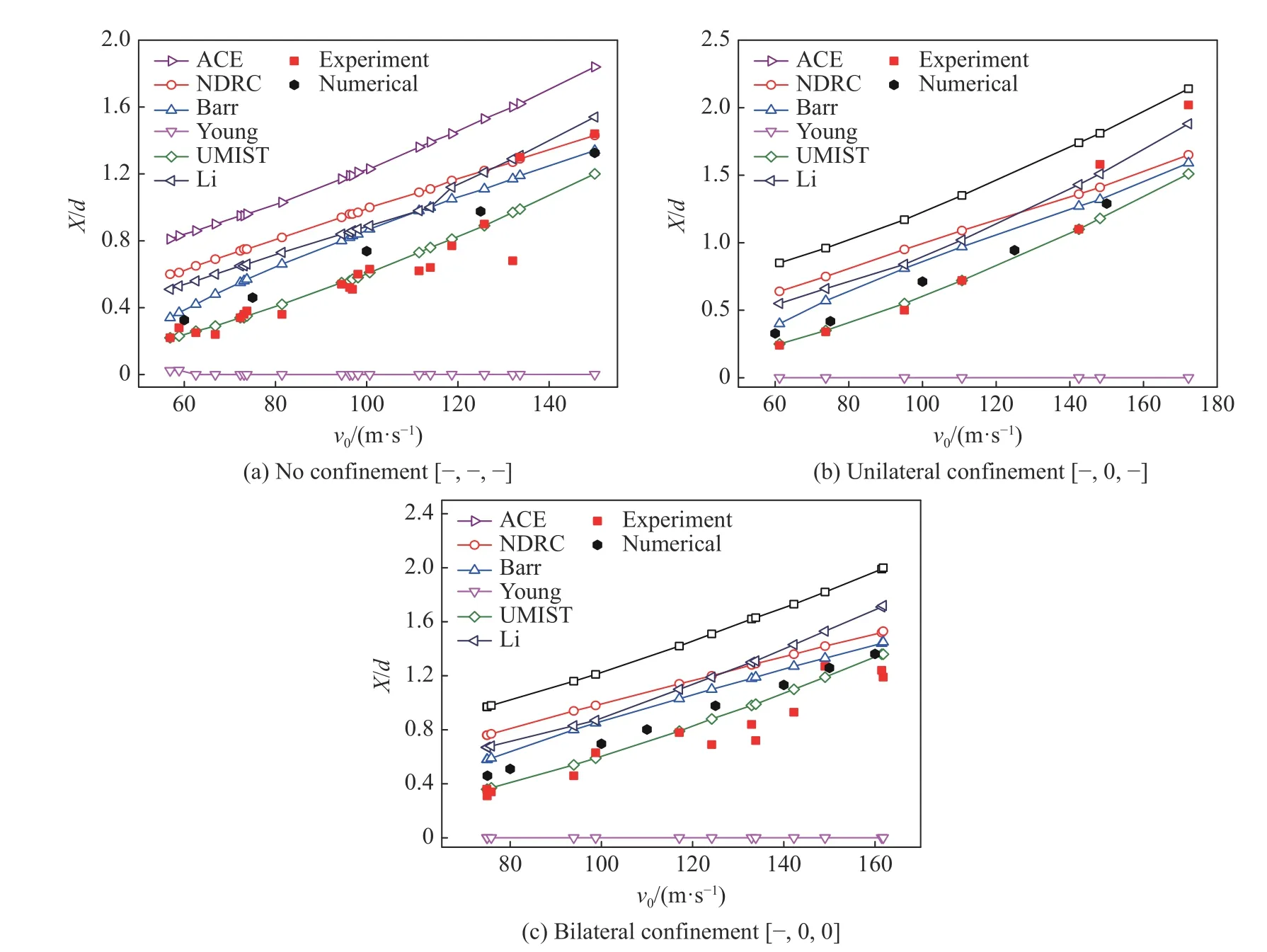
圖3 不同側限狀態下的開坑深度Fig. 3 Pit depths under different lateral confinements

在無側限、單向側限、雙向側限應力狀態下，UMIST 公式（式（6））的計算結果在沖擊速度較低時與實驗結果吻合很好。在低速沖擊條件下使用該公式預測不同應力狀態下的開坑結果比較有效。但是，當沖擊速度逐漸增大時，該公式的預測結果低于實驗結果。這是因為UMIST 公式主要是基于大量平頭彈低速侵徹實驗結果總結得到，適用范圍為：50 mm ＜ d ＜ 600 mm，35 kg ＜ M ＜ 2 500 kg，0 ＜ X/d ＜ 2.5，3 m/s＜ v0＜ 66.2 m/s。

有限元計算結果與實驗結果也非常接近，表明HJC 模型對于開坑深度的計算是非常有效的。

ACE 公式（式（1））是基于彈體直徑為12.7～155.0 mm、混凝土靶板厚度h 與彈徑d 之比(h/d)為3～18 的沖擊實驗得到的，與本研究中無側限、單向側限、雙向側限應力狀態下的水泥砂漿侵徹實驗情況差別較大，因此ACE 公式的計算結果明顯高于實驗值。修正NDRC 公式（式（3））是在Kennedy 的補充修正基礎上得到的，實驗所用的彈體直徑也比較大，但是沖擊速度不是很高。對比結果表明：在沖擊速度較低時，修正NDRC 公式的計算結果與實驗結果的差距較大；隨著沖擊速度的增大，兩者的差距逐漸縮小，說明此時該公式具有較好的適用性。Barr 公式（式（4））主要針對低速范圍進行了修正，其計算值低于修正NDRC 公式的計算結果，而且在較低的沖擊速度下，該公式的計算值比修正NDRC 公式的計算值低得多，更接近實驗結果。Li 公式（式（7））中的撞擊函數是由Forrestal 等根據實驗結果擬合得到的，然后基于Forrestal 半經驗公式進行無量綱化，其計算結果與修正NDRC 公式的計算結果相交，即當沖擊速度較低時，該公式更接近實驗結果，而當沖擊速度較高時，該公式的計算結果與實驗結果偏離更多。由于實驗所用彈體的質量較小，超出了Young 公式（式（5））的適用范圍，因此Young 公式的計算結果遠低于實驗結果，幾乎趨于零。

圖3 所示的對比結果也表明，隨著實驗過程中試件側限程度的增加，這些公式的計算結果與實驗結果的符合程度更好。其原因在于，這些經驗公式的獲得雖然沒有強調應力狀態，但是基本上是基于大尺寸靶的實驗，在彈丸沖擊開坑過程中靶體實際上處于一定程度的側限約束。

2.3 應力狀態對開坑深度擬合結果的影響

為討論應力狀態對開坑深度擬合結果的影響，采用形式相對簡單的修正NDRC 公式，并對其形式進行適當修改，即

式中：C 和n 是由實驗確定的經驗常數；NN為彈頭形狀因子，對于平頭彈，取NN= 0.72；考慮到不同的初始應力狀態，將原來的單軸抗壓強度擴展為靶體的動態強度 f*， f*與應力狀態有關，是一種三軸應力狀態下的強度(MPa)。

擬合結果如圖4 所示，其中：n 為2.0，即無量綱開坑深度與彈丸初始動能相關；C 為4.2，較修正NDRC 公式中的C 值略大，與水泥砂漿材料強度有關；對于擬合強度 f*，雙向側限時最高，達到25.8 MPa，無側限時最低，為14.7 MPa，單向側限時為17.6 MPa。無側限時的擬合強度與M10 水泥砂漿試樣的單軸壓縮強度相當，表明初始應力狀態對開坑過程有較大的影響。

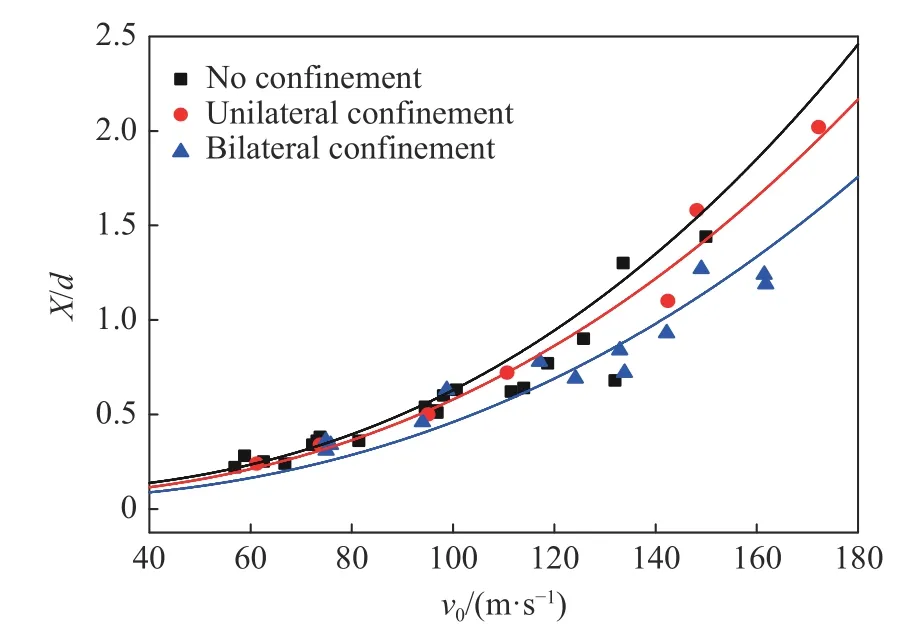
圖4 不同側限狀態下開坑深度的擬合[15]Fig. 4 Fitting results of pit depth under different lateral confinement[15]

需要注意的是，式(8)等號右邊是含量綱的，因此，此擬合結果對于其他尺寸的彈丸開坑須慎重使用。下面采用無量綱形式的擬合。

開坑深度主要受以下參數控制

式中： ρt、 Et、 μt、 ft分別為靶材的密度、楊氏模量、泊松比和無側限抗壓強度，v0、d、L、 ρp、 Ep、 μp、Yp分別為子彈的初始速度、直徑、長度、密度、楊氏模量、泊松比和屈服強度。

以 ρt、d 和ft作為基本量，則式（9）的無量綱形式為

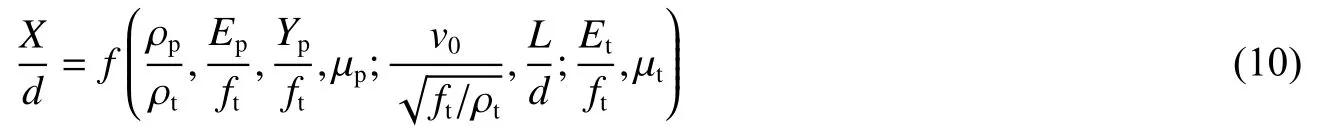
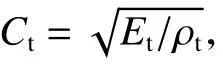
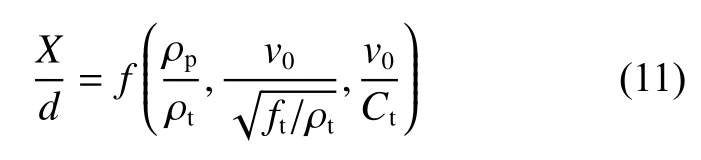
將泊松比等其他材料參數代入待定系數，則式（11）可初步表達為

擬合實驗數據，結果如圖5 和表3 所示。可見，水泥砂漿的開坑過程主要受強度特性影響，并且隨著側限的增強，影響增強。無側限條件下，慣性效應和壓縮特性對開坑的影響基本相同；隨著側限的增強，壓縮特性對開坑過程的影響增強，慣性特性減弱。因此，應力狀態對水泥砂漿的侵徹開坑過程有非常大的影響。

圖5 開坑深度的進一步擬合Fig. 5 Further fitting of pit depth

表3 無量綱侵徹深度公式參數Table 3 Formula parameters of dimensionless penetration depth

3 水泥砂漿中的侵徹阻力

3.1 侵徹過程測試

Forrestal 等[25]采用直徑為76.2 mm、質量為13 kg 的4340 鋼卵形彈對混凝土進行了沖擊速度為140～460 m/s 的侵徹實驗，通過在彈丸內部安裝單通道加速度數據記錄器，實時記錄彈丸的加速度波形。當混凝土無側限抗壓強度為23 MPa 時，預測與測量結果一致，如圖6（a）所示；而當抗壓強度為39 MPa時，在上升時間和峰值平臺響應上預測與測量結果一致，在侵徹即將結束時兩者有所偏差，如圖6（b）所示。王琳等[26]提出了一種采用應變片直接測量彈體變形的方法，對混凝土靶進行了速度范圍為150～300 m/s 的正侵徹實驗，記錄了彈體的應變時程曲線，如圖6（c）所示。這些實驗成功獲得了侵徹過程中彈體的響應，為計算提供了很好的依據。

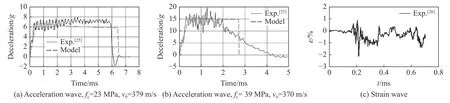
圖6 彈體侵徹過程中彈丸中的波形[25-26]Fig. 6 Recorded wave in the bullet during the penetration[25-26]

徐松林等[14]、陳麗娜等[15]應用真三軸混凝土侵徹實驗裝置，從另一個角度獲得了彈丸侵徹過程中混凝土的響應曲線，即通過與試件底端接觸的鋼桿傳遞并記錄侵徹過程中試件內的波形。圖7所示波形包含了多個過程：未開坑情況下（速度56.90 m/s），彈丸與試件彈性碰撞；開坑很淺（速度73.11～113.97 m/s）時，彈丸回彈；彈丸穩態侵入（速度150.00 m/s）時，形成較完整的開坑。

以上兩類實驗分別從子彈內部的加速度響應和穿過試件的波形來分析侵徹阻力的發展過程。加速度波形對開坑過程有一定的反映，其脈寬和幅值與未開坑情況對比有一定的變化。但是，由于還要考慮子彈高速沖擊時的結構響應、子彈頭部與試樣的局部接觸等因素的影響，因此加速度波形的變化與開坑過程的對應關系不是很直接，其定性的意義更強一些。對比而言，y 軸支撐桿上的信息傳遞的是試件開坑過程的直接響應，其應力波形變化對開坑過程的反映更敏感，更能揭示開坑過程的特征。本測試結果可為相關抗彈性能的計算提供多種邊界條件；同時，也可以結合加速度波形，形成更科學的抗彈性能計算和分析評估方法。由此可見，研究侵徹過程時，需要將二者有機結合。下面將結合數值分析對此過程進行討論。

圖7 模擬彈體侵徹過程中穿過試件的波形Fig. 7 Simulated wave profiles across specimen during penetration

3.2 沖擊速度對開坑過程的影響

采用數值分析方法模擬了不同彈速下水泥砂漿的抗彈情況。圖8 顯示了應力狀態為三向側限時不同彈速下各方向桿計算得到的結果。端部阻力、側面擴孔阻力及側面摩擦力幅值均隨彈速的增加而增加；隨著沖擊速度的增加，開坑效應越來越明顯，與圖7 所示形態一致。側面摩擦脈寬遠小于端部阻力與側面擴孔力脈寬，表明側面摩擦在開坑前期起主要作用。數值模擬結果所呈現的趨勢與實驗結果[15]基本一致。

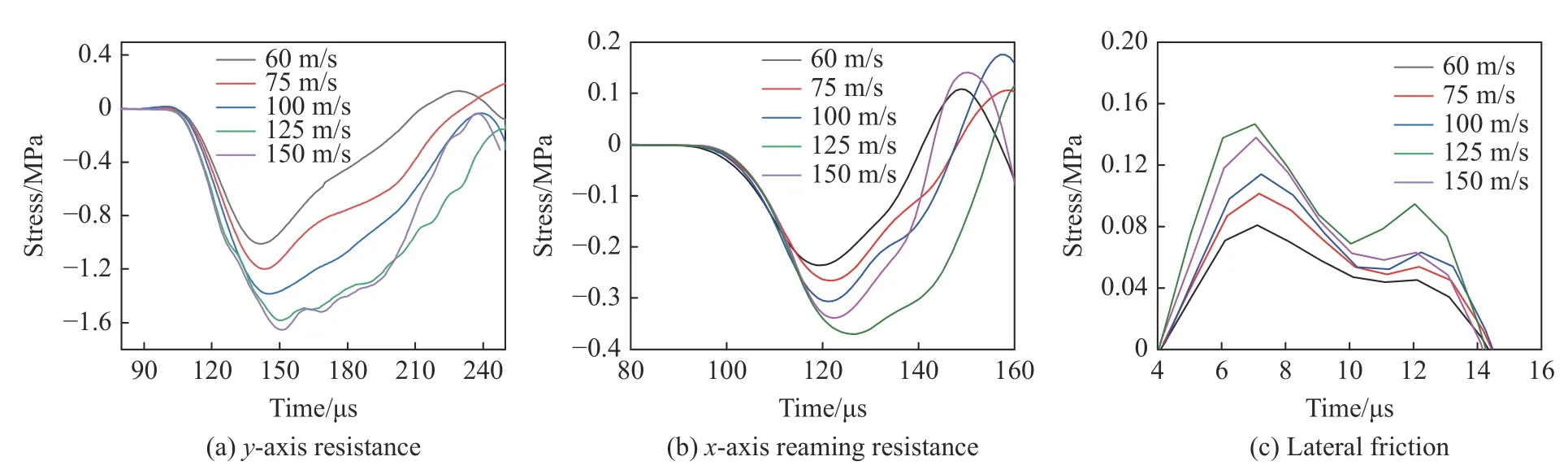
圖8 彈體侵徹過程中穿過試件的波形[15]Fig. 8 Wave profiles across specimen during penetration[15]

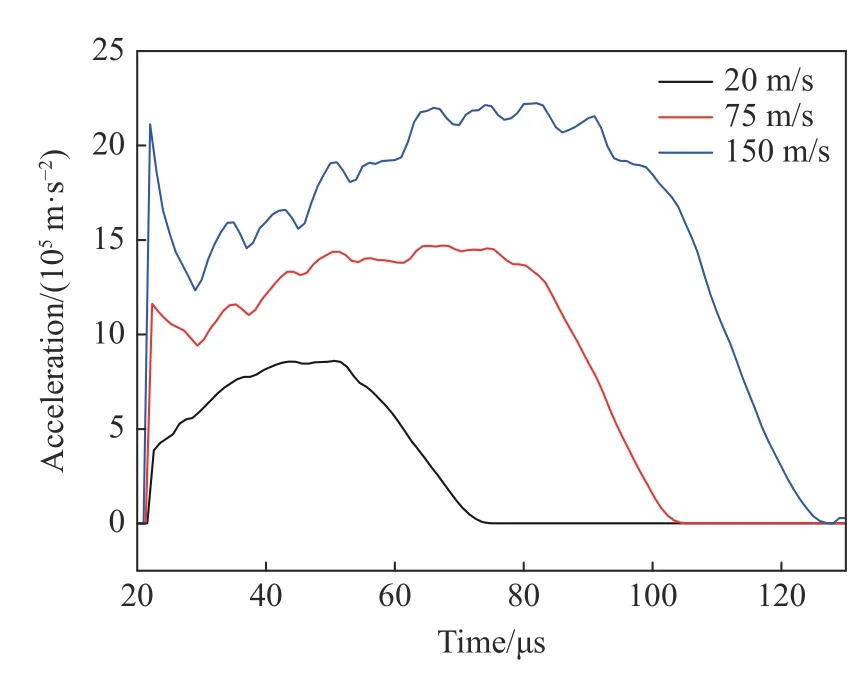
圖9 彈丸加速度時程曲線Fig. 9 Acceleration wave profiles in bullet

平頭彈速度為20、75 和150 m/s 時，分別實現了彈丸與試件彈性碰撞、開坑較淺及完整開坑3 種工況。圖9 顯示了三向側限時3 種速度下彈丸的加速度時程曲線。隨著彈丸速度的增加，彈丸端部加速度發展歷程出現一定差異，即加速度脈寬逐漸增加。計算結果與圖6(a)和圖6(b)所示的測試結果有較大差異，計算加速度曲線沒有明顯的平臺段。其原因在于：Forrestal 等[25]的實驗中，加速度記錄點位于彈丸內部，與撞擊端有一定的距離；本計算中，加速度記錄點在彈丸內部并接近靶材的撞擊端。在撞擊端附近，加速度波形能很好地反映開坑過程，然而受加速度測試元件埋設工藝所限，實驗中只能進行離撞擊端較遠處的加速度響應信息采集。在低速沖擊下，彈丸以開坑為主。以20 m/s 的速度碰撞靶體時，靶體處于彈性狀態，彈丸壓縮靶體后回彈，靶體沒有損傷，加速度波形沒有波動；隨著彈丸速度增加，彈丸碰撞靶體后，靶體開始破損，加速度曲線出現波動，波動幅度隨靶體破損程度的增加而增加。

計算結果表明：子彈內的加速度波形和y 軸支撐桿上記錄的波形都可以很好地反映彈丸開坑過程，理想的加速度波形需要通過靠近撞擊端的測點記錄。

3.3 應力狀態對開坑過程的影響

改變靶體初始應力狀態，模擬相同彈速下不同應力狀態的彈丸開坑過程。圖10 顯示了沖擊速度為150 m/s 時3 種應力狀態下各桿上應力計算結果。當靶體圍壓從8 MPa 增加至32 MPa 時，y 方向端部阻力的應力峰值隨著圍壓的增加而減小，脈寬隨圍壓的增加而增加；應力值的變化趨勢與實驗結果[15]一致，但脈寬變化存在一定差異。圖10(b)所示的側面膨脹力信號隨著圍壓的增加而明顯增強，波形呈現出明顯差異，表明初始應力狀態對開坑過程有較大影響，進行深部抗彈研究時需要給予足夠的重視。

圖10 應力狀態對波形的影響Fig. 10 Influence of stress state on waveform

4 討 論

綜合上述數值分析結果，可以看出：（1）HJC 模型計算的開坑深度從整體上看比較有效，其數值比實驗結果略高；（2）HJC 模型計算的端部阻力與實驗測試結果雖然在趨勢上比較一致，但是在數值上比實驗結果高很多。其原因比較復雜。

沖擊作用下水泥砂漿具有靜水壓效應和應變率效應，兩種效應是耦合的，如何分離尚沒有很好的方法。HJC 模型中僅考慮了應變率效應的影響，即在沖擊過程中通過引入率敏感項 (1+CHJCln)來考慮動態強度的增加。張磊等[27]的研究表明，混凝土材料的率效應具有分段特性，即存在多個CHJC值。HJC 模型中，狀態方程分為3 個階段，這3 個階段的靜水壓效應不同，而分段的應變率敏感項則是對不同階段的靜水壓效應的逐步考慮。本研究所采用的HJC 模型參數參考Meyer 的實驗結果，開坑深度的計算比較符合實驗結果，但是由于沒有采用分段式率效應表達，因此使用適用于較高沖擊速度的CHJC值是造成HJC 模型計算結果中坑深略高的原因。

HJC 模型中，第1 階段的靜水壓 p=Kμ， 第2 階段的靜水壓 p=pc+(μ－μc)(pl－pc)/(μp－μc)，第3 階段的靜水壓，為修正的體積應變。這種表達對于中等和較高的應力水平較好，而對于較低的應力水平則會產生較大的誤差。在前期較低的應力水平下，這類關系曲線的體積變形隨靜水壓的增加快速增長；但是，實際上當對試件施加三向圍壓時，由于側限的影響，試件沒有明顯的壓縮過程，即壓縮過程中試樣體積變形較小，而試樣靜水壓力值迅速增加，因此試樣所受的靜水壓力值隨著體積變形的增加快速增加。這是HJC 模型在保證坑深計算較好的情況下，卻得到較低應力水平的原因。要在較低沖擊速度下同時得到較好的坑深和應力模擬結果，需要將各階段的應變率效應和靜水壓效應等 參數納入模擬過程，把不同階段的材料特性完整呈現出來，建立一個較系統的新的模型參數。

5 結 論

基于真三軸應力狀態下水泥砂漿材料侵徹性能的實驗結果，進行了經驗公式計算、無量綱公式計算、有限元數值模擬對比研究，得到如下主要結論：

（1）應用基于HJC 模型的有限元方法分析開坑深度和開坑阻力，計算得到的開坑深度與實驗結果基本一致，但是應力與實驗結果差別較大，表明HJC 模型能有效模擬不同應力狀態下的開坑深度，但是卻只能定性描述開坑阻力；

（2）不同侵徹經驗公式對侵徹結果的預測存在一定的差異，其中UMIST 經驗公式對低速侵徹實驗深度的預測較為有效；

（3）雖然子彈加速度波形和y 軸支撐桿上記錄的波形都能反映彈丸開坑過程，但是y 軸支撐桿上表現的開坑特征更明顯，數值模擬結果中桿上的應力波形與實驗結果趨勢一致，應力峰值均隨著彈丸速度的增加而增加。