全浸水帶間隙發射高速射彈的入水沖擊載荷分析

魯春佳，侯 健，魏 平

（海軍工程大學兵器工程學院，湖北 武漢 430032）

全浸水帶間隙發射作為一種新的水下發射方式[1]，通過間隙燃氣在膛內貼壁運動，卷吸回流后逐漸匯聚成彈前氣幕，排出彈前水柱，將射彈在膛口的發射環境由水介質轉化為氣體介質。當氣體射流流出槍口后，膛口處射流迅速膨脹成球形氣體空腔，射彈穿過氣體空腔與水介質接觸，產生強烈的沖擊載荷。水下高速射彈的彈體主要由硬鋁合金尾桿和鎢合金頭部組成，兩者鑲嵌連接，連接強度有限，入水瞬間彈頭會承受巨大沖擊，因此射彈的入水沖擊載荷成為水下射彈設計中的一個重要問題。

Karman[2]最先開始對入水沖擊現象進行研究，采用動量定理并引入附加質量的概念，推導出入水沖擊載荷的計算公式。Wagner[3]將Karman 的方法理論化，提出了近似平板理論及自相似解法，得出了沖擊壓力在結構沾濕面的分布情況，使理論分析更加符合實際情況，為后來學者的理論研究奠定了基礎。在國內，秦洪德等[4]、王永虎等[5]對入水沖擊問題的現狀和進展進行了詳細的分析。宋保維等[6]基于不可壓縮的非定常勢流理論，建立了空投水雷入水沖擊計算的數學模型。盧熾華等[7]利用不同浸深的附加質量，對剛性細長體斜姿態落水沖擊進行建模，得出其入水角很小，會使彈體處在最危險的狀態。王永虎等[8-9]先后對剛性尖拱體垂直姿態高速入水和斜入水的沖擊理論進行了建模和仿真。魏卓慧等[10]建立了剛性截錐彈體垂直入水沖擊載荷的數學模型，并對其進行了數值計算。陳誠等[11]對超空泡航行器傾斜入水沖擊載荷進行了試驗研究，得出了峰值時刻的阻力系數。朱珠等[12]利用商業軟件FLUENT，建立了柱體回轉體高速入水沖擊的數值模擬模型，得到了速度對入水沖擊載荷的影響規律。然而以上研究主要針對由空中入水的沖擊載荷分析，對于水下入水沖擊問題研究較少。本工作在此前提條件下，計算分析全水下發射高速射彈入水的沖擊載荷，這對于水下發射武器研究具有一定的現實意義。

本研究擬建立錐形彈體水平及斜入水的沖擊載荷理論模型，模型中考慮彈體重力、彈體浮力、附加質量、彈頭錐角及入水攻角的影響，對不同頭部結構參數的錐形彈體以不同入水速度入水的沖擊載荷進行計算，分析入水速度、彈頭錐角和入水攻角對沖擊載荷的影響。研究結果對于彈體入水沖擊載荷的預測及全水下發射方式發射的射彈頭部結構設計具有參考價值。

1 數學模型

1.1 射彈水平入水

假設射彈為剛體，不考慮射彈入水時空泡的影響，根據動量定理，射彈高速入水沖擊時的動量方程為

式中：M 為射彈的質量，m 為射彈的附加質量， Fd為 射彈入水時受到的阻力， Fb為射彈所受的浮力。

對式（1）等號兩邊進行微分，得到射彈入水沖擊時的動力學方程

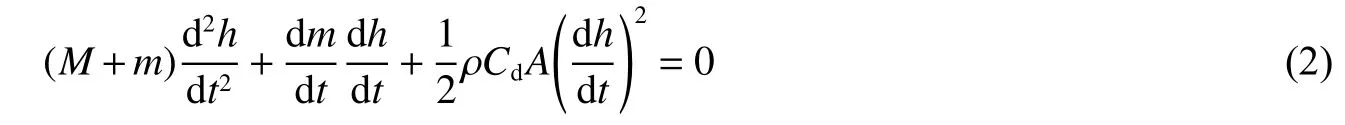
式中：h 為射彈侵入的距離，A 為阻力面積， Cd為 阻力系數， ρ為水的密度。

射彈沿 x 軸水平入水時，由于入水沖擊過程的瞬時性，入水初期其運動方向基本保持不變，流體動力主要作用于射彈軸線方向，在射彈軸線方向上重力和浮力對射彈影響很小，基本可忽略不計。

射彈入水沖擊過程中，射彈浸沒在水中的體積會排擠液面流體產生隆起現象，如圖1 所示，有效液面決定了自由水平液面的抬高程度，這取決于射彈錐頭的外形和入水角等初始狀態。沾濕因子定義為有效液面與實際液面的比值。

利用軸長體假設和Tayler 關于在不同浸深時附加質量的表達式[13]，參考垂直入水相關文獻[10,14]，求出錐形射彈入水的附加質量為

圖1 射彈水平入水沖擊示意圖Fig. 1 Schematic diagram of horizontal impact of the projectile

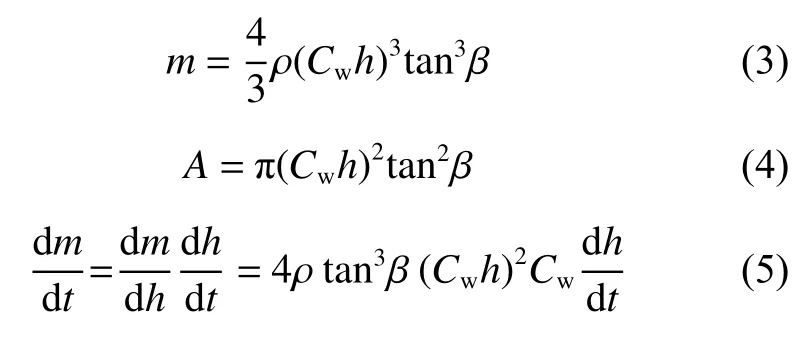
式中： Cw為 沾濕因子， β為射彈頭部的半錐角，如圖1 所示。

將式（3）～式（5）代入式（2），得到總方程為

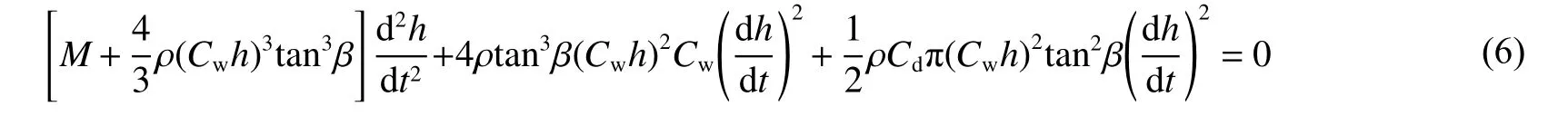
采用MATLAB 軟件，利用龍格-庫塔方法進行求解，可以得到彈體入水時的沖擊載荷。

1.2 帶攻角入水

如圖2 所示，采用全新的發射方式時，燃氣排出并在膛口形成球形氣體空腔。以地面為坐標系，槍口斜向上（即 y 軸正方向）、斜向下（即 y軸負方向）發射時，根據圓切線定理，穿過球形氣腔仍可看作垂直于液面入水，然而射彈入水在有攻角的情況下，軸向上會受到重力和浮力的作用分力影響，攻角正負值相反時，重力與浮力在射彈軸向上的作用分力方向也相反。

其他條件與水平入水時保持不變，攻角為正時，根據動量方程，得到動力學方程

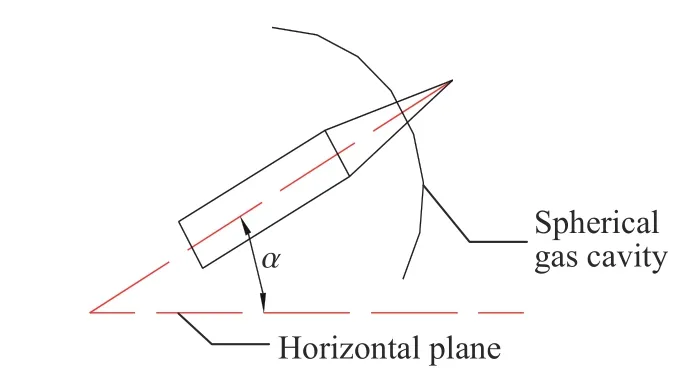
圖2 射彈攻角示意圖Fig. 2 Angle of attack of the projectile

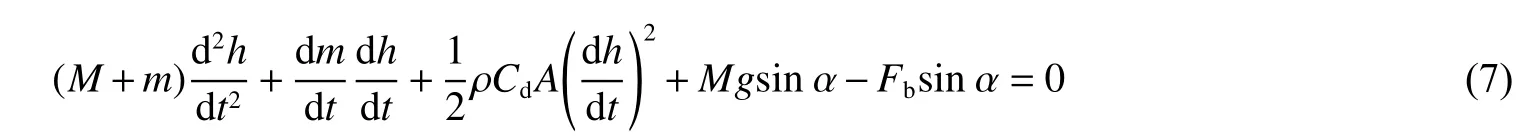
式中：α 為射彈攻角，射彈斜向上發射時為正值，斜向下時為負值。

射彈所受浮力為

當攻角為正值時，得到的總方程為

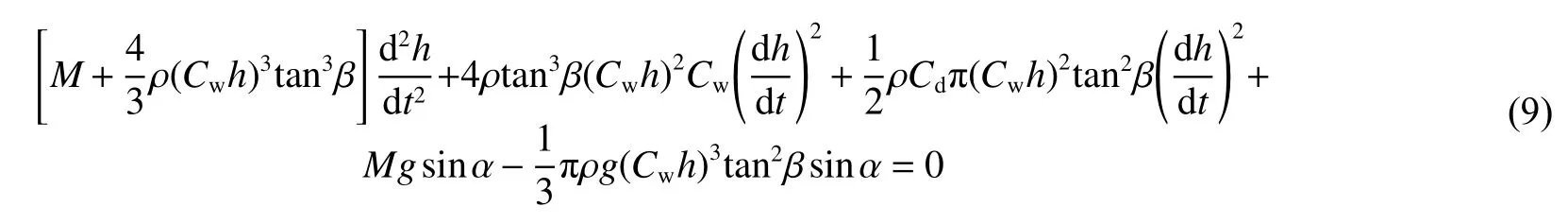
同理，攻角為負值時的總方程為

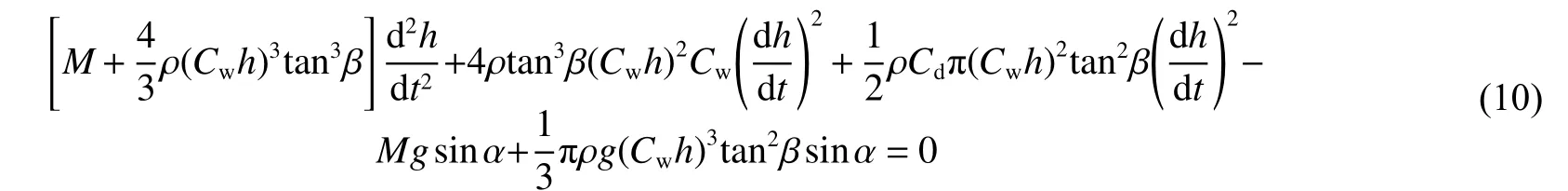
對式（9）、式（10）進行求解，可以得到不同攻角下的入水沖擊載荷。

2 計算結果與分析

由于水下射彈的質量較輕，入水速度較大，水下超空泡射彈入水平均速度約為600 m/s，因此入水速度對射彈入水沖擊載荷的影響很大。本計算中，設射彈質量為0.14 kg，射彈頭部半錐角為6°，計算得到不同速度時射彈的入水沖擊載荷曲線，如圖3 所示，其中用射彈加速度反映入水沖擊載荷。可以看出：射彈的入水沖擊載荷先增大后減小，載荷變化主要發生在射彈入水前1 ms，最后漸漸趨于穩定；入水速度越大，沖擊載荷峰值越大，入水后達到峰值的時間越短。此外，計算了不同速度下的入水沖擊載荷峰值，如圖4 所示。入水速度在400～700 m/s 范圍時，射彈入水沖擊載荷峰值一般為103g 量級（g 為重力加速度）。從沖擊載荷峰值與速度的關系可以得出入水沖擊載荷的峰值與速度基本呈線性關系。

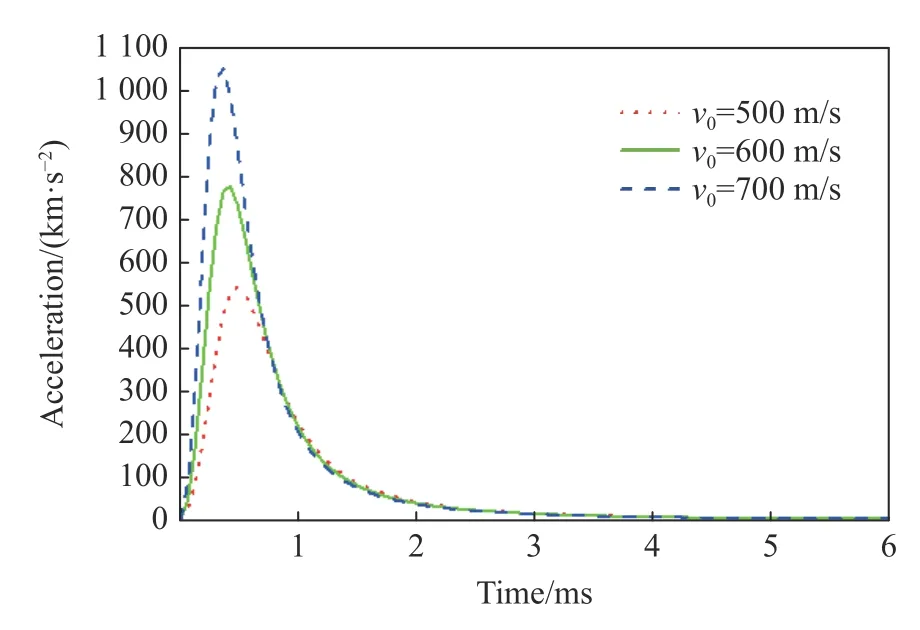
圖3 不同速度時的入水沖擊載荷Fig. 3 Driving impact loads at different velocities

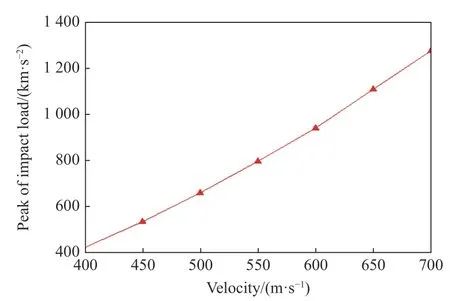
圖4 不同速度時的沖擊載荷峰值Fig. 4 Peak impact loads at different velocities

設射彈質量為0.14 kg，通過計算獲得了不同錐角的錐形射彈以600 m/s 入水時的沖擊載荷曲線，如圖5 所示。可以看出：射彈的入水沖擊載荷先增大后減小，最后趨于穩定；半錐角 β越大，沖擊載荷峰值越大，并且入水后達到峰值的時間越短。改變半錐角，計算出不同半錐角情況下射彈入水沖擊載荷峰值，如圖6 所示。從沖擊載荷峰值與半錐角的關系可以得出入水沖擊載荷峰值與半錐角基本呈線性關系。

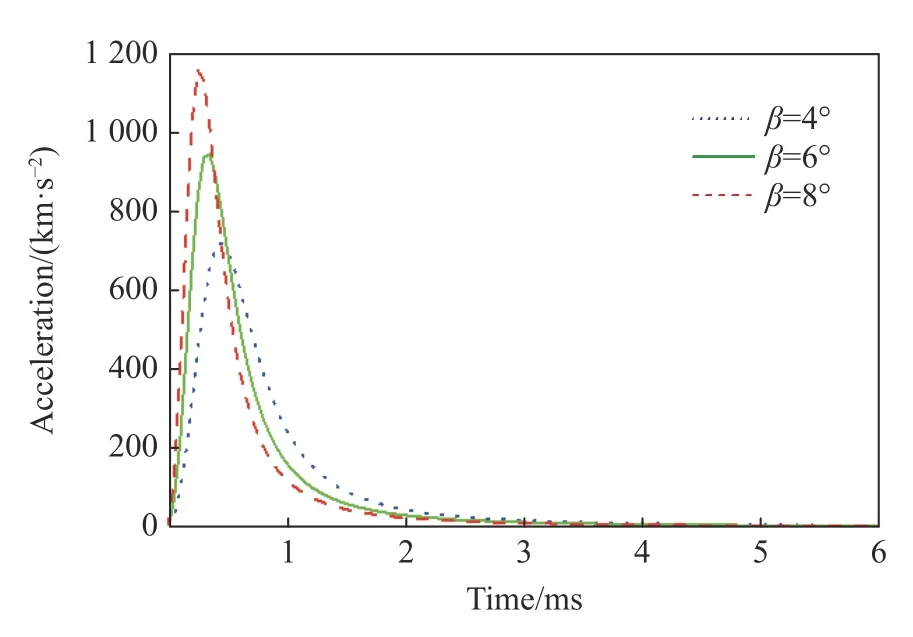
圖5 不同錐角時的入水沖擊載荷Fig. 5 Driving impact loads at different cone angles

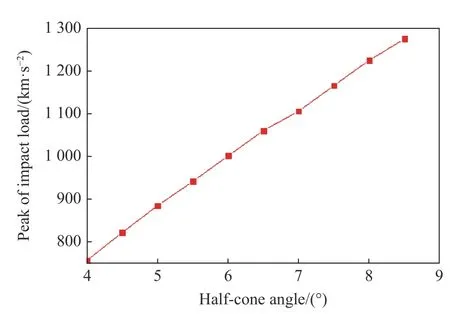
圖6 不同錐角時的沖擊載荷峰值Fig. 6 Peak impact loads at different cone angles

當射彈質量為0.14 kg，入水速度為600 m/s，攻角 α分別取45°、-45 °和0°（即水平入水）時，計算得到的射彈入水沖擊載荷曲線如圖7 所示。可見，3 條曲線基本重疊，差值在1g 量級，相比于速度和半錐角對沖擊載荷的影響，攻角對沖擊載荷的影響幾乎可以忽略不計。

此外，射彈在高速入水狀態下，從液面進入水中的實際深度與理想深度存在一定的偏差，為了表達該誤差，引入沾濕因子，沾濕因子的取值對沖擊載荷的結果也存在影響。沾濕因子不同時射彈的入水沖擊載荷如圖8 所示。從圖8 可以看出：沾濕因子越大，入水沖擊載荷峰值越大；但沾濕因子對入水沖擊 載荷的影響較小，當沾濕因子變化值為0.1 時，入水沖擊載荷的變化在10%以內。

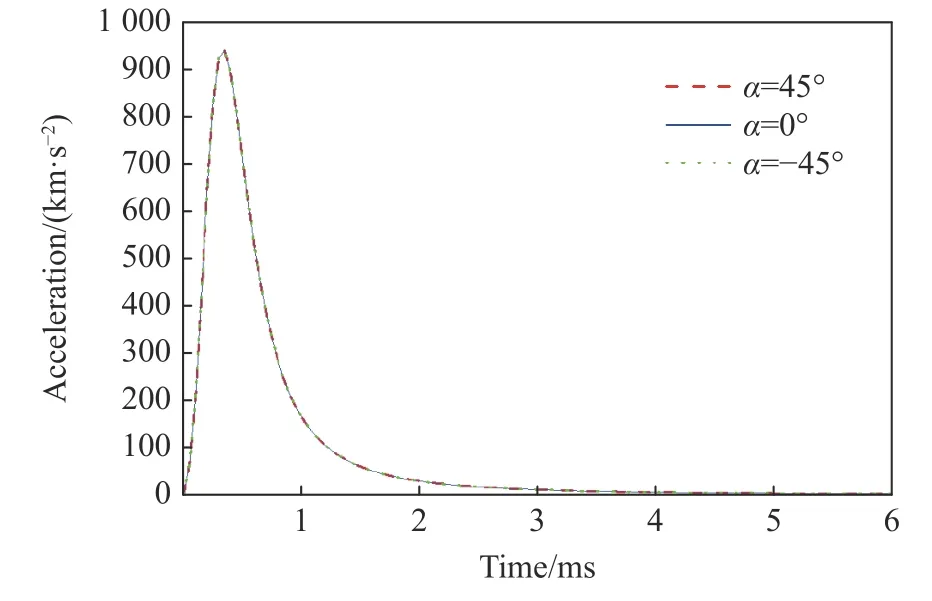
圖7 不同攻角時的入水沖擊載荷Fig. 7 Inlet impact loads at different angles of attack

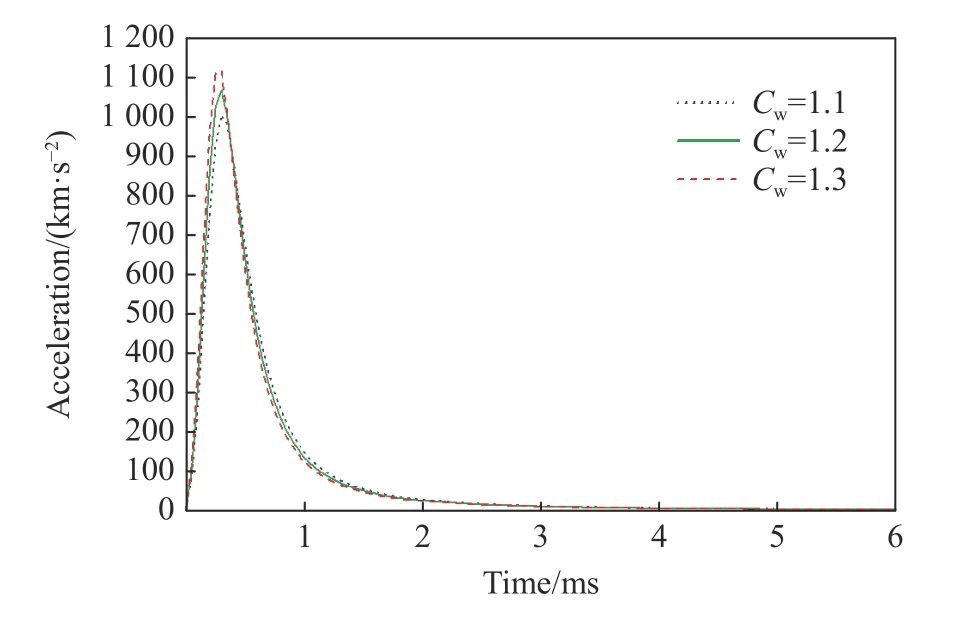
圖8 沾濕因子不同時的入水沖擊載荷Fig. 8 Inlet impact loads with different wet factors

3 結 論

（1）射彈頭部錐角相同時，入水沖擊載荷峰值與速度呈正線性相關，入水速度越大，沖擊載荷達到峰值的時間越短；射彈入水速度相同時，入水沖擊載荷的大小與錐角呈正線性相關，錐角越大，沖擊載荷達到峰值的時間越短。

（2）射彈錐角和入水速度相同、入水攻角不同時，入水沖擊載荷曲線與水平入水曲線基本重合，說明射彈重力和浮力在軸向上對入水沖擊載荷的影響相對入水阻力幾乎可以忽略不計。當射彈帶有攻角入水后，重力和浮力更多的是對射彈產生徑向力矩影響。

（3）沾濕因子越大，入水沖擊載荷峰值越大，但對入水沖擊載荷影響較小，當沾濕因子變化為0.1 時，入水沖擊載荷的變化在10%以內。沾濕因子作為一個變量，其大小反過來也取決于入水沖擊載荷，入水沖擊載荷越大，沾濕因子也越大。

（4）理論模型借鑒了高速彈體垂直入水的理論模型，數值模擬計算結果與已報道的高速射彈垂直入水沖擊載荷數值計算和仿真結果高度一致，驗證了本數學建模和數值計算的準確性。

（5）探討了全水下發射高速射彈入水瞬間的沖擊載荷，高速射彈入水后形成超空泡，沖擊載荷迅速減小。本工作對射彈未形成超空泡的情況進行了模型推導和數值模擬計算，對形成超空泡之前的理論研究具有重要意義。