基于改進蟻群算法的圖像輪廓高精度分割研究

李巧蘭，盧永祥，盧榮輝

(武夷學院 信息技術與實驗室管理中心，福建 龍巖 354300)

為辨識和分析目標，需要將圖像中的目標部分分割出來，在此基礎上才可對目標進一步分析利用，由此產生了圖像分割技術，即分割出圖像中存在目標部分的區域的過程。因圖像分割的質量對后續的分析產生直接的影響，所以分割技術算法的精度至關重要[1]。當前，國內外已經提出上千種圖像分割的算法。安霆[2]提出利用遺傳算法處理圖像噪聲，結合進化代數和個體的適應度值提高了圖像分割的效率。高蕊[3]等學者提出基于螞蟻算法提取圖像的灰度、梯度和鄰域特征，實現圖像分割算法的外廓提取。但傳統算法存在分割效率低、精度差、穩定性不佳等弊端。

針對傳統算法的不足，提出了基于改進蟻群算法的圖像輪廓高精度分割算法研究，首先構建一種圖像分割路徑幾何模型，基于蟻群算法進行迭代尋優找出最短路徑，并基于GPU技術修正偏差，完成對圖像分割的精確計算和控制。實驗結果表明，提出的算法設計路徑最短、精度高、算法穩定性好。

1 一種圖像輪廓目標點間距分布式算法研究

1.1 圖像分割路徑幾何模型的構建

通常采用圖像分割的圖像的構造較為復雜，由曲線、圓弧、直線等多種元素組成。要準確地計算圖像輪廓目標點的間距，可以采用一種分布式的計算模式提高算法的精度[4-5]。首先來構建圖像輪廓目標點分割的幾何模型，為圖像分割設定好工作路徑[6-7]。設待分割加工的圖像幾何輪廓由直線和圓弧等元素組成，如圖1所示。

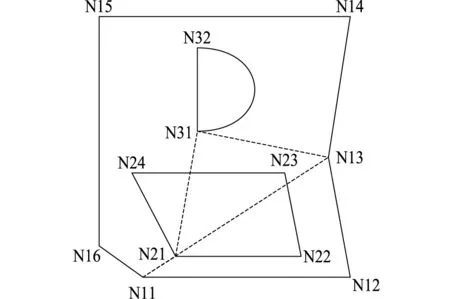
圖1 圖像輪廓的幾何圖形

如圖1所示，圖像輪廓由外環和2個內環組合而成，外環和內環都是由邊Ei和定點Ni組合而成，那么外環可以定義為N11-N16，兩個內環可以分別定義為N21-N24和N31-N32。圖像輪廓分割時，要先分割內環，再分割外環[8]，比如以點N21為開始的分割點，分割后再從該點逐漸移動到其他定點，并充分考慮圖像分割時對圖像輪廓形變的影響[9]。

將外環定義為L1，內環分別定義為L2和L3，那么內環L2和L3之間的最短間距，可以使用兩環定點之間的最短距離dij來定義[10]：

(1)

其中(xik,yik)和(xjk,yjk)分別為L2和L3定點的坐標。圖像輪廓分割過程中產生的空行程是外環與內環距離及內環之間的距離的和[11]，圖像輪廓分割的幾何模型D可以表示為：

D=dij+dik+dik+…+dmo

(2)

圖像輪廓目標點間距分布式計算的目的就是要找到使總距離Dmin最短的路徑[12]。基于對最短路徑的分析，構建圖像輪廓分割的幾何模型，此時需要找出一條確保空程最短的最優行進路徑。這是一個極為復雜的過程，需要確定目標點的具體位置，并選擇分割順序[13]。不同的目標點位置和不同的分割順序都會產生不同的空程長度[14]。假設圖像的環數為n，每個環的頂點數量為m1，這時圖像輪廓分割路徑的條數ki可以表示為：

(3)

對于最優路徑的選擇問題，采用了改進蟻群算法，基于螞蟻行進路徑中遺留的信息素濃度和啟發因子的變化情況，進行反復的迭代尋優找出最優的分割路徑，并提高圖像輪廓目標點間距的控制精度。

1.2 基于改進蟻群算法圖像輪廓目標點間距分布式計算的實現

蟻群算法是一種仿生學算法，適用于路徑尋優，蟻群算法易于與其他的方法相結合、魯棒性高[15]。改進的蟻群算法，能夠在圖像輪廓分割過程中選擇一條最短路徑，并實現對圖像輪廓目標點間距的最優控制。螞蟻在覓食過程中，基于信息度濃度選擇最短路徑。如果路徑上的信息素的濃度越大，選擇這條路徑的概率就越大。路徑尋優的過程，如圖2所示。

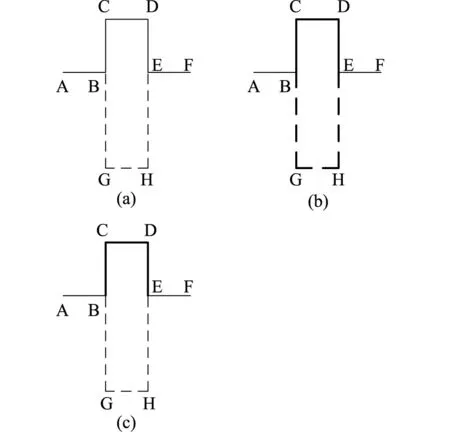
圖2 路徑尋優示意圖

A點是蟻巢，F點是食物源，由于從A點到F點之間存在障礙物，因此有兩條繞過障礙物的路徑供選擇，分別是ABCDEF和ABGHEF，其中設定ABGHEF路徑中BG與HE段長度是ABCDEF路徑中BC與DE段長度的2倍。

假定在蟻巢和食物源之間移動螞蟻個體數量是200，那么在初始時刻由于沒有螞蟻個體通過，各段路徑上的螞蟻信息素濃度指標都為零。當螞蟻開始在路徑上移動時，這種行為是隨機的即在ABCDEF和ABGHEF兩條路徑上都有螞蟻存在。基于概率學原理，螞蟻個體選擇兩條路徑的概率是相等的。因此，存在于兩條路徑上的螞蟻數量是相同的。螞蟻個體在向前行進的過程中，會在沿途釋放信息素，如果螞蟻留下的單位信息素相同，根據上述設定的ABGHEF與ABCDEF路徑長度，得出路徑BG與HE段的信息素濃度是BC與DE段的2倍，而后再通過的螞蟻個體就會有較大的概率選擇ABCDEF路徑，這樣就找到了一條到達食物源的最短路徑。

基于改進蟻群算法的圖像輪廓高精度分割算法具有分布式特點。分布式結構[16-18]具有很強的適應性，盡管依賴于系統中的個體行為，但其中某一個個體行為的失效又不會影響系統整體的結構和功能。對于圖像輪廓分割的路徑優化與選擇問題，采用基于改進蟻群算法的圖像輪廓目標點間距計算模式，體現出了分布式算法的優勢。

螞蟻根據路徑上的信息素濃度信息選擇路徑，路徑上的信息素隨著螞蟻的移動而改變，同時隨著時間的推移而揮發，設在蟻群中的螞蟻個體的數量為a，在t時刻在路徑i，j上的信息量表示為ζij(t)，bi(t)表示t時刻在路徑i附近的螞蟻個體數量，則有：

(4)

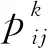
(5)

式(5)中，sij(t)為螞蟻個體在路徑i，j行進的過程中所釋放的信息量、α為啟發因子(對螞蟻行進路徑的選擇起到了至關重要的作用)、β為期望啟發因子、ξik(t)是局部路徑啟發函數，可以表示為：

(6)

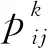
基于仿生學的原理，螞蟻個體在前進過程中釋放的信息素的濃度會不斷地增強，同時隨著時間的推移，每條路徑的總信息素含量也會不斷地揮發，即信息素的濃度是動態可變的，t+n時刻在路徑i，j上的信息素變化過程如下：

(7)

式(7)中，Δsij(t)表示信息素的增量，在初始時刻Δsij(t)為零，用常數κ表示螞蟻行進過程中在沿途釋放信息素的揮發系數，κ?[0,1)，那么(1-κ)即為信息素的殘留系數。設lk為螞蟻k在路徑尋優時，所走過的總路程長度，τk表示螞蟻沿路釋放信息素的強度，這時Δsij(t)的求解公式為：

(8)

沿著信息素的增量路徑尋優，能夠找到一條最佳的路徑，并能夠保證圖像輪廓目標點間距精度最高。經典蟻群算法的不足是迭代尋優和整個計算耗時都較長。采用GPU算法將尋優過程中的數據進行串行計算和連接，并在GPU上運行，實現對經典蟻群算法的加速。由于改進蟻群算法中的全部個體行為都具有一致性，螞蟻個體依據相同的規則進行路徑尋優、互不干擾；但螞蟻個體之間并不直接聯系，而是采用遺留信息素的形式互相協作，這樣操作適用于并行運算。

采用了改進的蟻群算法，對圖像輪廓目標點間距進行分布式計算，基于螞蟻行進路徑中的信息素含量來判定最優路徑，并實現對圖像輪廓分割的精確控制。

2 實驗部分

為驗證所提方法在切割路徑尋優和圖像輪廓分割的高精度，進行了一組仿真實驗，從實際路徑長度、迭代次數和圖像輪廓分割精度等方面進行對比驗證。

2.1 算法參數設定

基于改進蟻群算法的最優路徑尋優過程受到其幾何模型中各種參數的影響，各種差異化的參數組合會對算法的收斂性能、測量精度產生不同的影響。路徑尋優過程中的最佳參數組合，如表1所示。

表1 基于改進蟻群算法的參數組合設定

2.2 實驗結果與分析

基于所提方法，在圖像輪廓分割的輪廓目標點最短路徑選擇方面具有明顯的優勢，與文獻[2]方法對比，實際的分割路徑曲線分別如圖3和圖4所示。

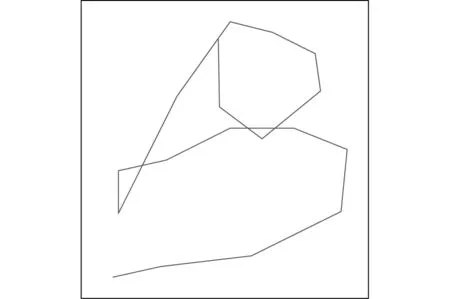
圖3 文獻[2]方法的路徑

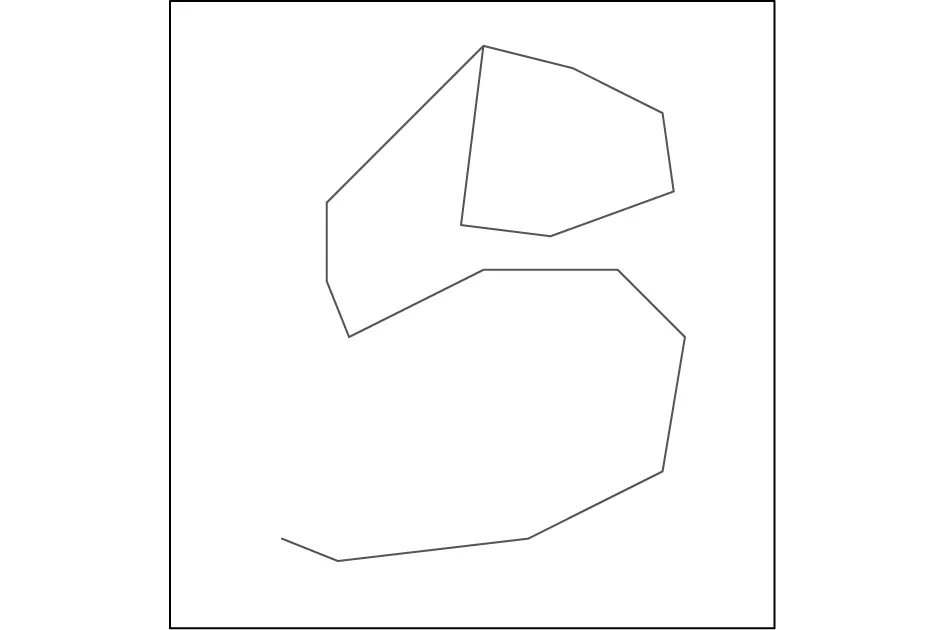
圖4 所提方法路徑

兩種算法的路徑長度統計，如表2所示。

表2 兩種算法的路徑統計/mm

分析圖3和圖4的路徑及表2的路徑統計，所提方法算法的路徑更短、無交叉、效率更高。文章分析了基于改進蟻群算法圖像輪廓高精度切割路徑尋優和圖像輪廓分割精度運算控制時的迭代次數變化曲線，如圖5所示。

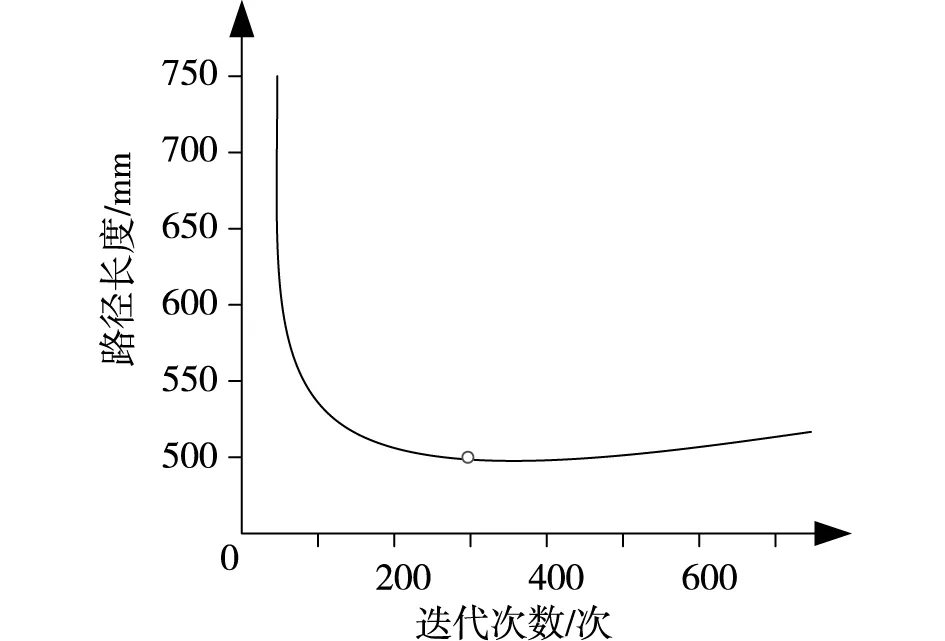
圖5 圖形間距精度與迭代次數的關系

如圖5所示，所提方法算法在迭代300次時就能夠尋找到最優路徑，其迭代次數明顯優于傳統尋優方法。

在圖像輪廓分割精度控制方面，分別采用文獻[2]方法和所提方法算法進行運算，提取了兩種算法下的精度測量值與理論值的數據對比結果，如表3所示。

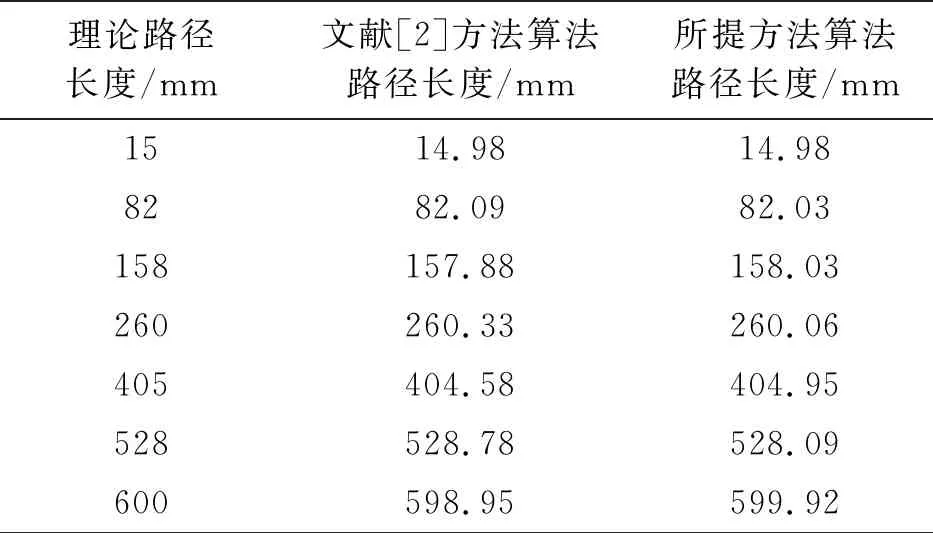
表3 圖像輪廓目標點間距精度控制對比/mm

表3的數據對比顯示，所提方法更接近理論值，計算精度更高，說明目標點兼具精度的控制效果更理想。

3 結論

圖像分割技術在圖像識別分析領域有著十分廣泛的用途。基于此設計了一種基于改進蟻群算法的圖像輪廓高精度分割算法研究，利用改進蟻群算法在迭代尋優方面的優勢，識別出最優路徑并提高圖像輪廓目標點間距控制方面的精度。