賦值法處理抽象函數(shù)問(wèn)題
李小蛟
(四川省成都市樹德中學(xué) 610091)
解答抽象函數(shù)題目的基礎(chǔ)是熟悉函數(shù)的基本知識(shí).抽象函數(shù)無(wú)具體表達(dá)式,要通過(guò)我們所學(xué)的一般初等函數(shù)的性質(zhì)來(lái)解決比較困難(小題可借用一些類似函數(shù)解決),但抽象函數(shù)問(wèn)題的解決本質(zhì)上是將抽象問(wèn)題具體化,所以解決抽象函數(shù)問(wèn)題可以將函數(shù)中變量具體賦值,即解決抽象函數(shù)有一個(gè)萬(wàn)能的方法——賦值法.下面我們分類例析用賦值法解決抽象函數(shù)問(wèn)題.
一、賦值法處理抽象函數(shù)的函數(shù)值
抽象函數(shù)求值問(wèn)題是要解決具體函數(shù)值問(wèn)題,因此抽象函數(shù)求值問(wèn)題的關(guān)鍵在于賦值,即賦要求解自變量,代入求出相應(yīng)函數(shù)值即可.
例1已知f(x)的定義域?yàn)镽,對(duì)任意的x,y∈R,有f(x+y)=f(x)+f(y),則f(0)=____.
分析本題函數(shù)沒(méi)有具體表達(dá)式,即抽象函數(shù)求值問(wèn)題,要求解f(0)的值,即在f(x+y)=f(x)+f(y)這一式子中要出現(xiàn)f(0),所以我們令x=y=0,即出現(xiàn)f(0+0)=f(0)+f(0),所以f(0)=0.
例2定義在R上的函數(shù)f(x)滿足f(x+y)=f(x)+f(y)+2xy(x,y∈R),f(1)=2,則f(3)=____,f(-3)=____.
分析根據(jù)題意,已知f(1)=2且f(x+y)=f(x)+f(y)+2xy,要求解f(3),f(-3)的值,即要利用賦值法構(gòu)造出自變量為3,-3.
因?yàn)閒(1)=2,令x=y=1,所以f(2)=f(1+1)=f(1)+f(1)+2×1×1=2+2+2=6.
又令x=2,y=1,所以f(3)=f(2+1)=f(2)+f(1)+2×2×1=6+2+4=12.
現(xiàn)已求出f(3)=12,要求f(-3).注意3與-3互為相反數(shù),所以如果令x=3,y=-3,即有f(0)=f(3-3)=f(3)+f(-3)+2×3×(-3),因此我們還應(yīng)先求出f(0).于是再令x=y=0,則有f(0+0)=f(0)+f(0)+2×0×0,所以f(0)=0.
因此0=f(0)=f(3-3)=f(3)+f(-3)+2×3×(-3)=12+f(-3)-18.
所以f(-3)=6.
二、賦值法處理抽象函數(shù)解析式
抽象函數(shù)求解析式是要求出f(x),因此我們要采用賦值法得到f(x),并利用賦值法將對(duì)應(yīng)法則f作用的其余形式消去即可.
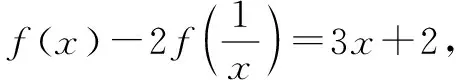
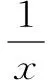
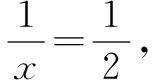
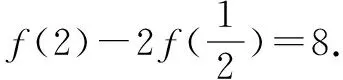
①

②
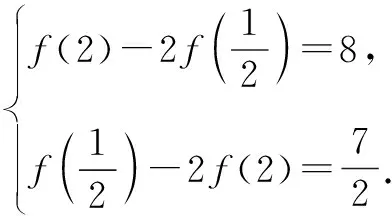
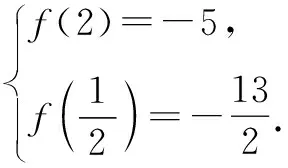
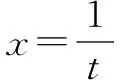
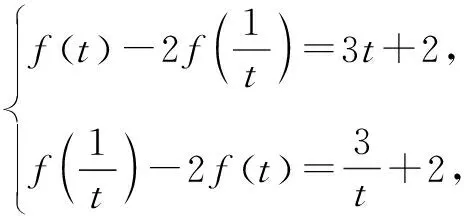
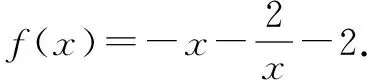
例4已知f(x)+2f(2-x)=3x2-8x+8,求f(x).
分析條件中給出有關(guān)對(duì)應(yīng)法則f作用于x和2-x,要求出f(x),就要想辦法消去f(2-x),所以利用賦值法,我們只需要將上式中所有x換為2-x,即f(2-x)+2f(x)=3(2-x)2-8(2-x)+8,然后與f(x)+2f(2-x)=3x2-8x+8聯(lián)立求解出f(x)=x2.
三、賦值法處理抽象函數(shù)奇偶性
奇偶性是考查f(x)和f(-x)之間的關(guān)系,所以抽象函數(shù)奇偶性問(wèn)題關(guān)鍵在于采用賦值法讓題目出現(xiàn)f(x)和f(-x),并根據(jù)表達(dá)式探究f(x)和f(-x)兩者的關(guān)系.
例5設(shè)函數(shù)f(x)的定義域?yàn)镽,對(duì)任意x1,x2∈R,恒有f(x1+x2)=f(x1)+f(x2)成立,則f(x)是____(指明函數(shù)的奇偶性).
分析令x1=x,x2=-x,則出現(xiàn)f(x-x)=f(x)+f(-x),所以f(x)+f(-x)=f(0),所以我們還要先求出f(0)的值.于是我們又令x1=x2=0,所以f(0)+f(0)=f(0),于是f(0)=0,所以f(x)+f(-x)=0,即f(x)為奇函數(shù).
例6設(shè)函數(shù)y=f(x)(x∈R且x≠0)對(duì)任意非零實(shí)數(shù)x1,x2滿足f(x1·x2)=f(x1)+f(x2),則函數(shù)y=f(x)是____(指明函數(shù)的奇偶性).
分析本題要出現(xiàn)f(x)和f(-x),我們只需令x1=x,x2=-1,則出現(xiàn)f(-x)=f(x)+f(-1),所以我們要先求出f(-1)的值,于是我們將所求f(-x)=f(x)+f(-1)中x的值賦為1,所以就有f(-1)=f(1)+f(-1),因此我們還得求出f(1)的值.我們?cè)僭陬}設(shè)中令x1=x2=1,所以f(1)=f(1)+f(1),求解出f(1)=0,再依次代入可得f(-1)=0,進(jìn)而f(-x)=f(x),即f(x)為偶函數(shù).
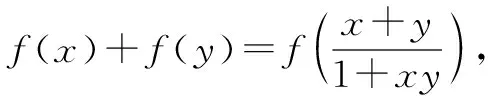
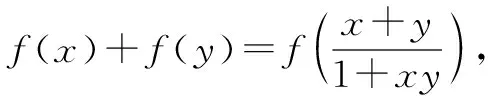
四、賦值法處理抽象函數(shù)單調(diào)性
函數(shù)單調(diào)性研究自變量大小與相應(yīng)函數(shù)值大小的關(guān)系,即在一個(gè)單調(diào)區(qū)間內(nèi)x1
例8已知f(x)的定義域?yàn)镽,對(duì)任意的x,y∈R,有f(x+y)=f(x)+f(y),且當(dāng)x>0時(shí),f(x)<0,求證:f(x)為(-,+)上的減函數(shù).
分析由例5已經(jīng)知道f(x)為奇函數(shù),任取x1,x2∈R,且x1>x2,則x1-x2>0.
所以f(x1)-f(x2)=f(x1)+f(-x2)=f(x1-x2).
因?yàn)楫?dāng)x>0時(shí),f(x)<0,
所以由x1-x2>0,可知f(x1-x2)<0.
所以當(dāng)x1>x2時(shí),有f(x1) 分析由例7已經(jīng)求出f(x)為奇函數(shù). 由x1-x2<0,且-1 又1-x1·x2>0,且1-x2>0,x1+1>0, 因?yàn)楫?dāng)0 所以當(dāng)-1 所以當(dāng)-1 所以f(x)在(-1,1)上為單調(diào)減函數(shù). 抽象函數(shù)求最值問(wèn)題可類比求值問(wèn)題,但經(jīng)常會(huì)綜合考查抽象函數(shù)的單調(diào)性、奇偶性等問(wèn)題,以及化歸與轉(zhuǎn)化、類比等數(shù)學(xué)思想方法. 例10已知f(x)的定義域?yàn)镽,對(duì)任意的x,y∈R,有f(x+y)=f(x)+f(y),且當(dāng)x>0時(shí),f(x)<0,若f(1)=-2,求f(x)在[-2,4]上的最大值和最小值. 分析由例5已經(jīng)知道f(x)為奇函數(shù),由例8得出f(x)為(-,+)上的減函數(shù). 因此f(x)在[-2,4]上最大值應(yīng)該為f(-2),最小值應(yīng)該為f(4),下面用賦值法分別求出f(-2),f(4). 因?yàn)閒(1)=-2, 所以f(2)=f(1+1)=f(1)+f(1)=-4. 所以f(-2)=-f(2)=4. 所以f(4)=f(2+2)=f(2)+f(2)=-8. 即f(x)在[-2,4]上最大值應(yīng)該為4,最小值為-8. 抽象函數(shù)不等式問(wèn)題需借助抽象函數(shù)的單調(diào)性、奇偶性、定義域等來(lái)綜合求解,利用賦值法將看似無(wú)關(guān)聯(lián)的不等式轉(zhuǎn)化為常規(guī)不等式問(wèn)題求解. 分析由例7已經(jīng)知道f(x)為奇函數(shù),由例9得出f(x)為(-1,1)上的減函數(shù). 由以上例析我們可以發(fā)現(xiàn),解決抽象函數(shù)問(wèn)題的本質(zhì)是將抽象問(wèn)題具體化,而通過(guò)賦值法幾乎可以解決抽象問(wèn)題的所有題型,因此賦值法不失為處理抽象函數(shù)問(wèn)題的一個(gè)最常用方法.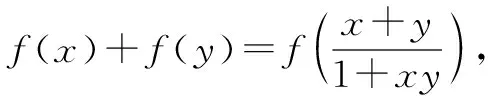

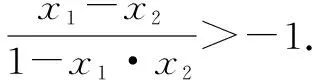
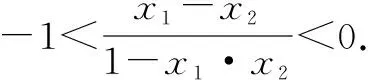
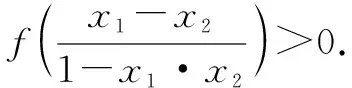
五、賦值法處理抽象函數(shù)最值
六、賦值法處理抽象函數(shù)不等式