錯位疊加曝光法制作楔形斜面微結構研究

董立文， 宋曉欣， 顧仁權， 張 鋒， 袁廣才， 姚 琪， 呂志軍， 劉文渠， 崔 釗

(京東方科技集團股份有限公司，北京 100176)

1 引 言

近年來，隨著液晶顯示技術的發展日漸成熟，人們對顯示體驗的需求越來越多樣化，促使各種不同應用場景的新型顯示器件層出不窮，如裸眼3D顯示[1-2]、指向式顯示[3-4]、透明顯示[5-6]等顯示器件。為實現這類顯示器件的不同功能，通常在器件結構設計方面提出特殊需求，如光柵結構、斜面反射結構、高PS結構等等，不僅對材料特性提出較高的要求，對制作工藝也帶來很大的挑戰。

對于裸眼3D顯示技術或指向式顯示技術，為達到相應顯示效果，通常會在器件內部制作斜面反射微結構，形成特定光場，使入射光或出射光按照設定光路沿特定角度進行反射，從而實現裸眼3D或特定角度顯示的顯示效果。目前，從工藝角度來講，對于楔形微結構的形成，最佳的制作手段是納米壓印技術[7]，其形成微結構的斜角精度最高、斜面平坦度最好，但該技術對設備和材料要求極高，且壓印模版制作成本較高，而且為形成顯示器件內部特定光路，對微結構位置精度要求在1 μm以內，但納米壓印技術控制的層間對位精度最高為10 μm，很難將光學微結構精準地壓印在特定位置。此外，灰階曝光技術[8]也可以實現斜面結構的制作，通過制作具有連續灰階的光罩，實現UV透過率在一個方向連續變化，使光阻在該方向接收UV劑量也連續變化，最終使顯影后的光阻呈現斜面形貌。但具有灰階的掩膜 (Gray Tone Mask，GTM)實現灰階的方式是形成不同間距的縫隙，每個縫隙的寬度相同，間距沿特定方向逐漸遞增或遞減，而且為實現灰階變化的連續性，縫隙需做得很窄(<1 μm)，導致這種光罩的加工難度高，制作成本高。

本文基于T公司生產的某型號正性光阻，采用錯位疊加曝光的方法，實現灰階曝光的效果，最終得到具有特定角度的楔形微結構的斷面形貌，并通過實驗對該型號光阻的UV光吸收系數以及使光阻發生分解反應的臨界曝光能量進行計算。

2 模型建立與計算

2.1 錯位疊加曝光

本文提出的錯位疊加曝光技術是一種利用常規掩膜版達到灰階曝光效果的光刻工藝技術，無需使用灰階曝光掩膜。工藝過程如下：在完成一次曝光后，移動一定距離再次進行曝光，然后按相同方向再次進行移動和曝光，如圖1所示。每次移動的距離及曝光次數根據微結構斜面角度而定。

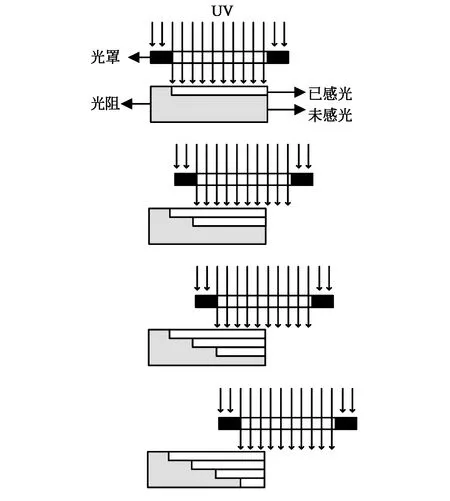
圖1 錯位疊加曝光方法原理圖Fig.1 Diagram of dislocation and superposition exposure method

2.2 模型計算

光阻的曝光、顯影以及固化過是一個極其復雜的過程。為進行簡單計算并表征出最終的光阻形貌，首先將理想斜面結構等效成臺階狀結構，分別稱之為理想模型和等效模型，根據Lambert-beer定律[9]：

I=I0E-αh

(1)

其中：I0為初始UV光能量值，I為使光阻中感光劑PAC不能再繼續反應的臨界曝光能量值，α為光阻對UV的吸收系數。

由于采用錯位疊加曝光方案實現灰階曝光，對于光阻的某個區域在縱向上并非只進行一次感光，而是多次感光，而且光阻經過UV感光的區域與未經感光的區域對UV的吸收系數不同，因此需要對上述關系進行轉化。如圖2所示，光阻UV感光的順序從Step1到Step4，假設未感光光阻吸收系數為α，感光區域光阻吸收系數為α′，可得到如下關系：

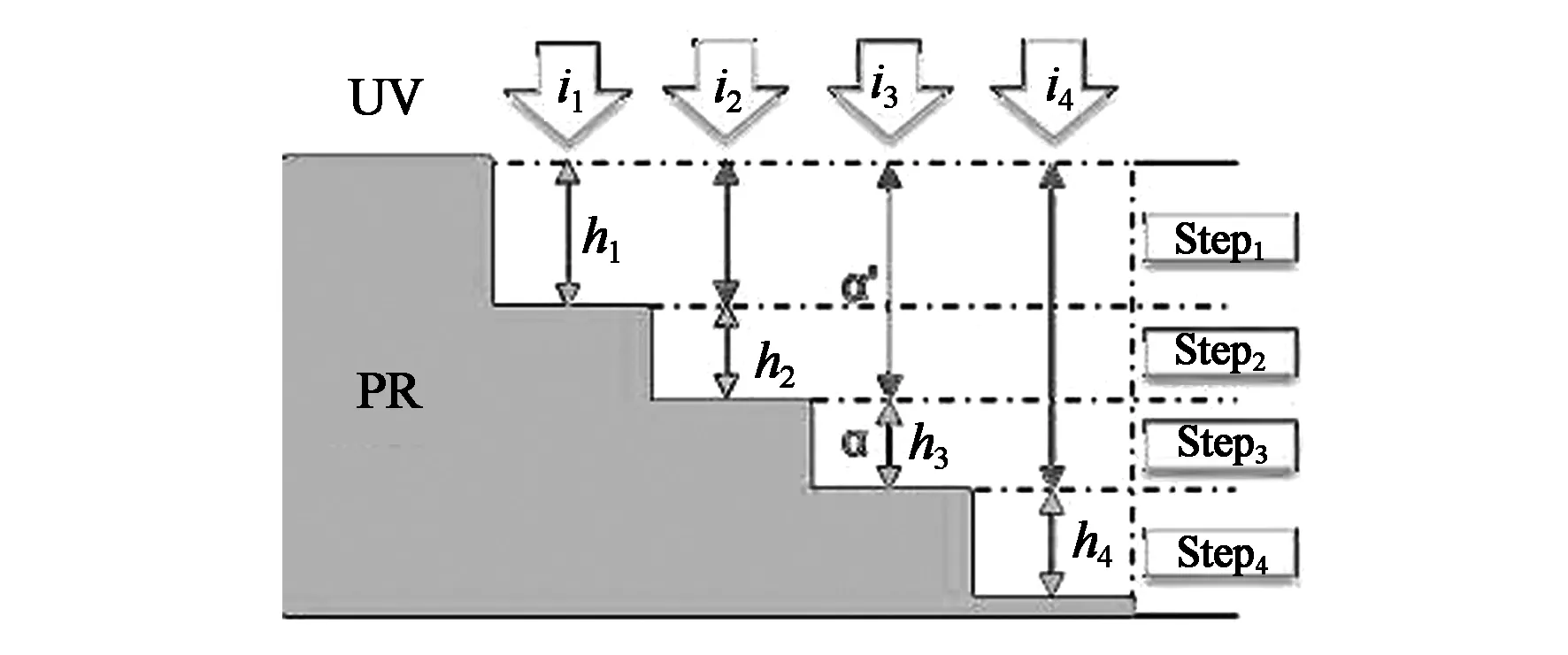
圖2 錯位疊加曝光效果示意圖Fig.2 Schematic diagram of exposure effect of dislocation and superposition

I=i1E-αh1

(2)

(3)

I=i3E-[α′(h1+h2)+αh3)]

(4)

I=i4E-[α′(h1+h2+h3)+αh4)]

(5)

根據以上關系，可以對i值、α以及α′進行計算，然后根據上述方法計算出每個Step需要的曝光能量。

3 實驗過程

3.1 正性光阻

實驗采用T公司生產的一款正性紫外感光光阻，主體成分為聚酰亞胺前體(Polyimide precursor)、γ-丁內酯(GBL)、乳酸乙酯(EL)、丙二醇單甲醚醋酸酯(PGMEA)以及添加劑。

3.2 實驗過程

根據上述模型，可以計算出錯位疊加曝光過程中，每次感光所需的曝光能量值。為得到曝光能量，首先需要3個重要的參數，即光阻在感光前后對UV光的吸收系數α、α′以及光阻發生光化學反應的臨界曝光能量I值。為得到上述參數，設計以下實驗。

實驗用基板為康寧(CORNING)公司生產的Lotus-TM NTX系列玻璃，玻璃尺寸為370 mm×470 mm，厚度為0.5 mm。在玻璃進行涂膠之前，需進行清洗處理，然后將光阻均勻涂覆在玻璃基板表面。本實驗采用旋涂方式進行涂膠，然后用熱板進行前烘工藝(Soft Bake)，前烘溫度為120 ℃，時間為500 s。曝光工藝過程采用兩種方式進行：(1)錯位疊加曝光的每次UV照射能量相同；(2)每次UV照射能量不同。曝光過程完成后進行顯影工藝，顯影方式為噴淋式顯影(Spray)，顯影時間為3 min，顯影液為濃度2.38%的TMAH，最后在烘箱中進行固化，固化溫度230 ℃，時間60 min。以上實驗完成后，計算并得到吸收系數α和α′， 以及光阻發生光化學反應的臨界曝光能量I值，最后計算得到每一次錯位疊加曝光的能量值。為證明錯位疊加曝光法的準確性，再次進行涂膠、前烘、曝光、顯影以及熱固化實驗進行驗證，實驗參數不變。

4 結果與討論

在進行錯位疊加曝光的過程中，當每次UV照射能量相同時，根據Lambert-beer定律，等效模型中每個臺階的感光情況如下：

Step1:I=i1E-αh1

(6)

(7)

Step3:I=i3E-[α′(h1+h2)+αh3)]

(8)

因為i1=i2=i3，可得：

(9)

圖3為SEM的測試結果，Step0區域的光阻未進行感光處理，光阻厚度約5.2 μm，說明涂膠實際厚度約為5.2 μm。當UV的照射能量值超過90 mJ時，第三次進行錯位疊加曝光后，Step3區域的光阻基本無殘余厚度，說明能量為270 mJ的UV光已經使5.2 μm厚的光阻完全感光并完全顯影。根據h1和h2測試數據(表1)可計算得到如下關系：

(10)

(11)

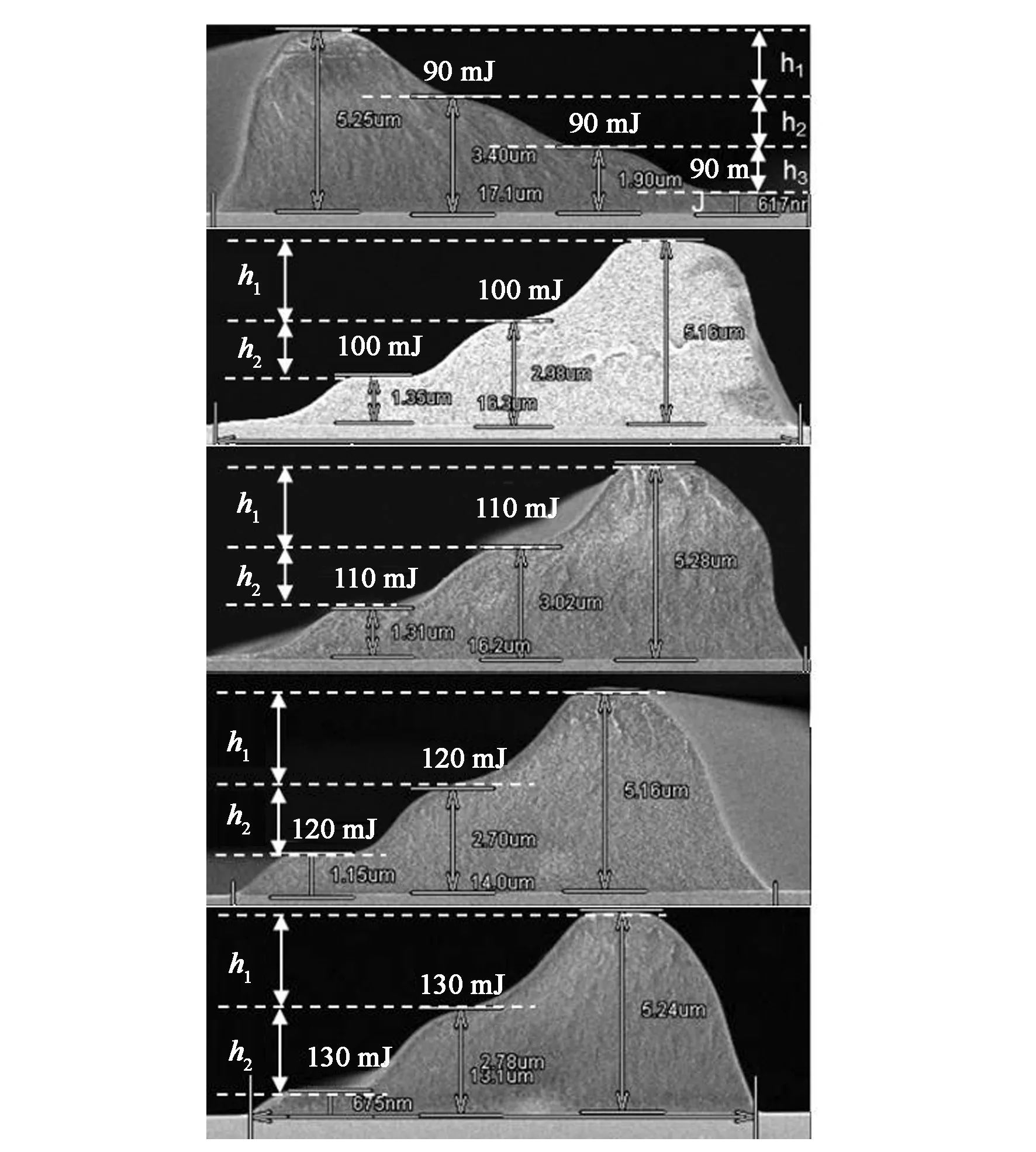
圖3 錯位疊加曝光能量相同情況得到的光阻形貌Fig.3 Photoresist profile obtained by the same exposure energy of each dislocation

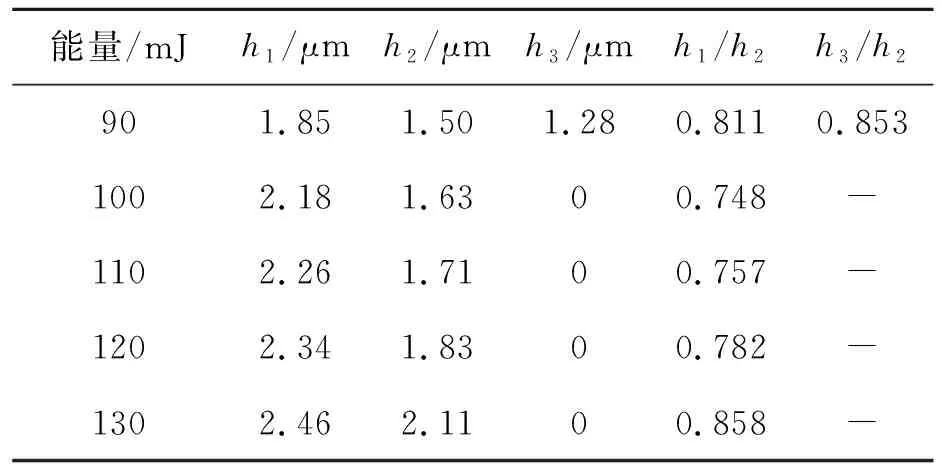
表1 錯位疊加曝光能量相同情況的h值Tab.1 h value at the same exposure energy of etch dislocation

但由于每次進行錯位疊加曝光的i值相同，通過上述實驗數據無法計算出具體的α值以及I值，因此需要進一步實驗，對每個Step采用不同的曝光能量進行曝光，目的是為了引入i變量，求得α值以及I值。

當錯位疊加曝光每次的UV照射能量不同時，即i值不同，根據Lambert-beer定律。等效模型中每個臺階的感光情況如下：

Step1:I=i1E-αh1

(12)

(13)

Step3:I=i3E-α′(h1+h2)E-αh3

(14)

可以根據Step1和Step2感光情況得到如下關系：

(15)

且α’≈0.2α，最終可得如下關系：

(16)

將圖4及表2中測試數據i的能量值和h段差值代入上述公式，計算α約為1.14；再將α值代入Step1公式，可計算出I值，計算結果I約為8 mJ，也就是說使光阻不在進行進一步反應的UV能量約為8 mJ。最終根據以上實驗及測試數據的計算結果，求得α約為1.14，α′約為0.22，I值為8 mJ。

圖4 錯位疊加曝光能量不同情況得到的光阻形貌Fig.4 Photoresist profile obtained by the different exposure energy of each dislocation

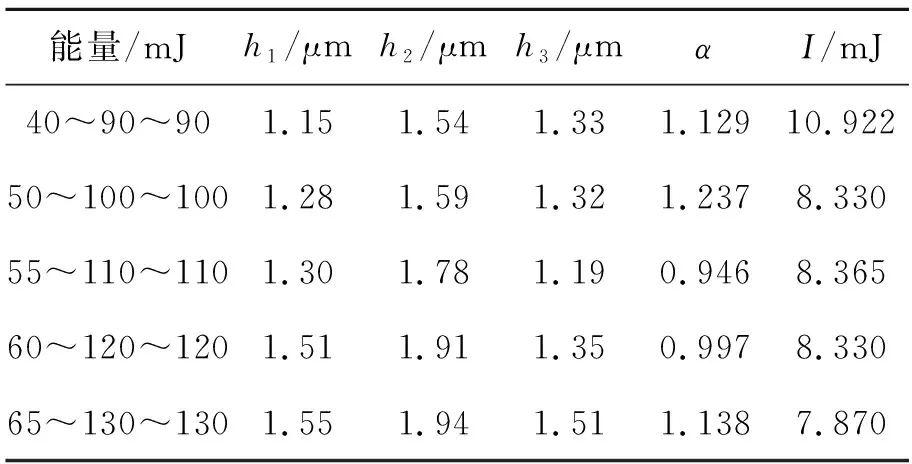
表2 錯位疊加曝光能量不同情況的h值Tab.2 h value at the different exposure energy of etch dislocation

基于以上數據，分別制作兩種不同高度的斜面結構對上述理論進一步進行驗證實驗，判斷I值和α值的準確性。首先需要計算出每次錯位曝光需要的能量i，設定斜面目標高度分別為3.7 μm以及7.5 μm，斜角θ目標值為32°，根據以上數據，按照Lambert-beer定律，分別計算出錯位疊加曝光過程中每次感光能量大小，如表3所示。

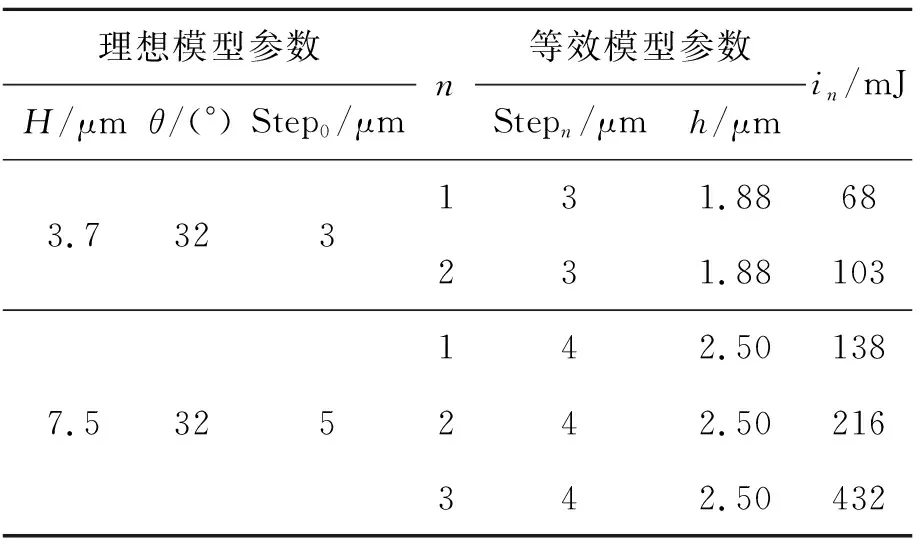
表3 基于I值和α值計算錯位疊加曝光的能量值Tab.3 Each dislocation exposure energy calculated based on the I and α value

對于第一種高度的結構，楔形斜面反射結構高度H為3.7 μm，斜面角度θ為32°時，從圖5的SEM數據中可以看出Step1的曝光能量60 mJ不變時，Step2曝光能量從110 mJ增加至140 mJ，所得到的楔形斜面的底角θ在31°～33°之間變化，結構高度H在3.69～3.74 μm之間變化，該結構基本符合目標值。如圖5(d)所示，當Step2的曝光能量增加至140 mJ時，該區域的光阻殘留厚度降低，最終導致斜面底角θ增大至40°，與目標值偏差較大。

對于第二種高度的結構，楔形斜面反射結構高度H為7.5 μm，斜面角度θ為32°，從圖6的SEM數據中可以看出，圖6(a～d)中Step1和Step2的曝光能量分別為100 mJ和200 mJ不變，而圖6(a)Step3曝光能量為200 mJ時，斜面的底角θ約為27°，主要原因是Step3區域光阻接受到總的曝光能量為500 mJ，能量過低，導致Step3區域殘留光阻厚度過大，最終使斜面的底角θ偏小。如圖6(b)、6(c)中樣品SEM數據所示，當提高Step3總的曝光能量至600～700 mJ時，即i3的能量為300～400 mJ時，所得到的楔形斜面的底角θ約為33°，結構高度H在7.10～7.34 μm之間變化，該結構基本符合目標值。但圖6(a～c)中樣品的斜面底角θ為36°，主要原因為Step4區域接收到的總曝光能量過高，約為1 100 mJ，而圖6(a～c)中樣品Step4區域接收到的總曝光能量卻為1 000 mJ，過高的曝光能量會提高衍射影響程度，導致Step3區域光阻殘余厚度降低，最終使斜面的底角θ偏大。另外，對于圖5中樣品Step3～Step5的能量選擇以及圖6中樣品Step4的能量選擇，因該區域不需要殘留光阻，只要該區域光阻所接收的UV能量足以使光阻完全發生反應并對相鄰Step區域光阻因衍射不至于產生過大影響即可。

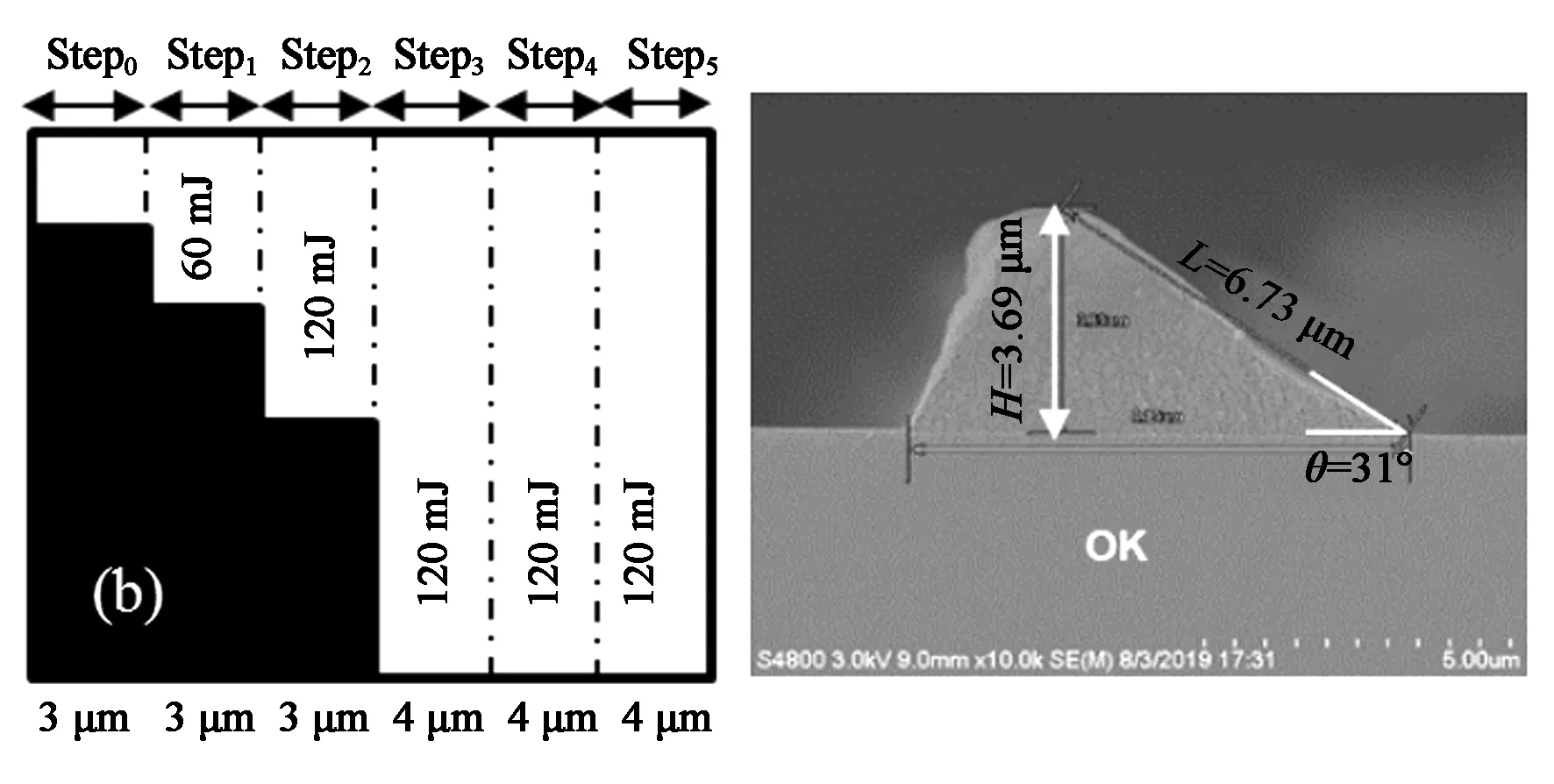
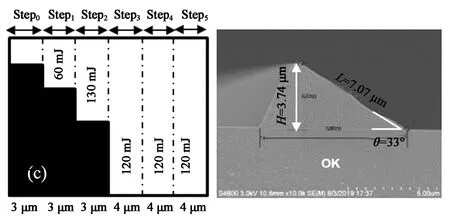
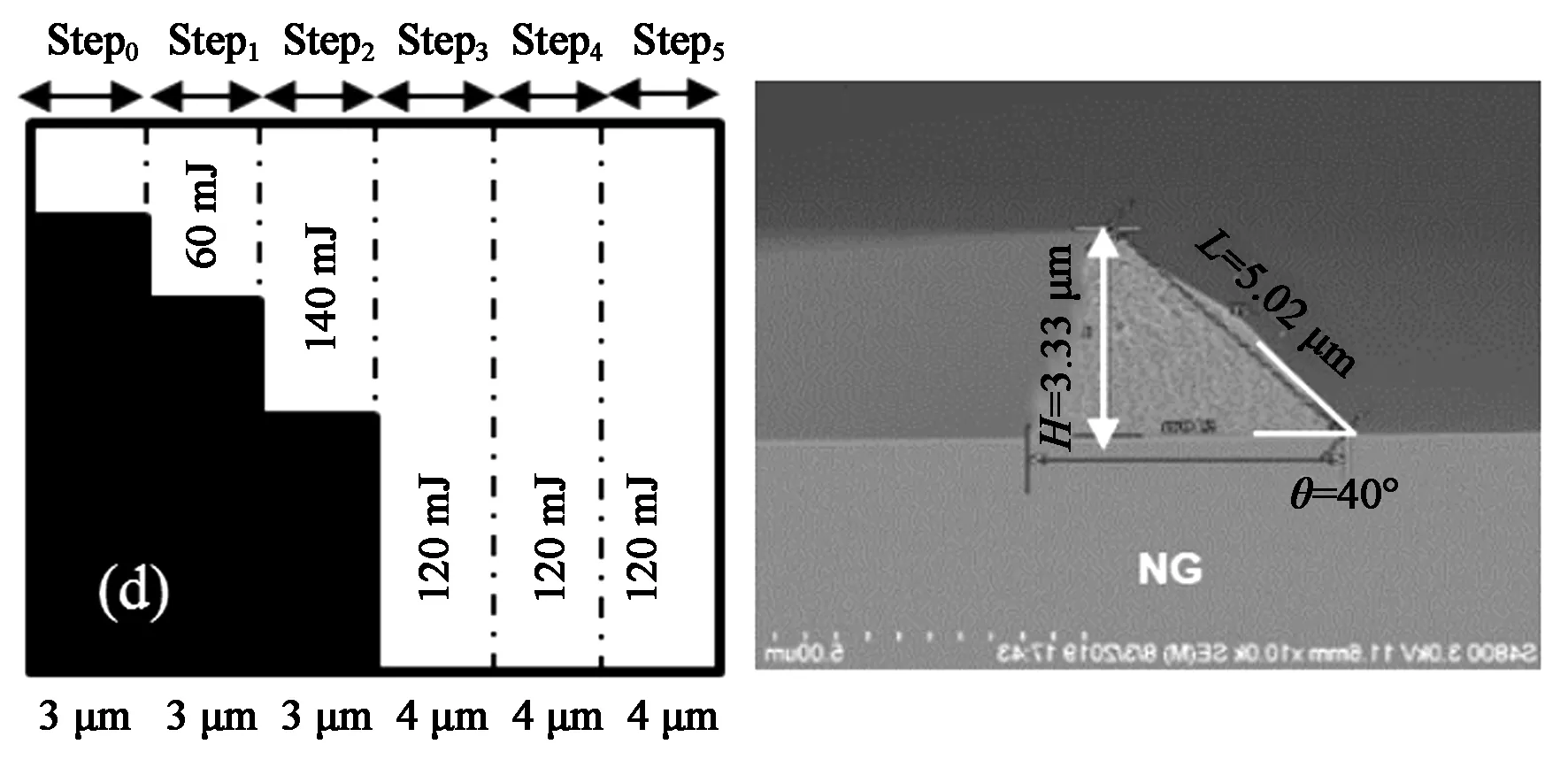
圖5 不同曝光條件(左)得到的相應楔形光阻形貌(右)(H=3.7 μm)。(a) Step2=110 mJ；(b) Step2=120 mJ；(c) Step2=130 mJ；(d) Step2=140 mJ。Fig.5 Wedge-shaped photoresist profile obtained under different exposure conditions (H=3.7 μm). The images on the left represent the exposure condition. (a) Step2=110 mJ； (b) Step2=120 mJ； (c) Step2=130 mJ； (d) Step2=140 mJ.

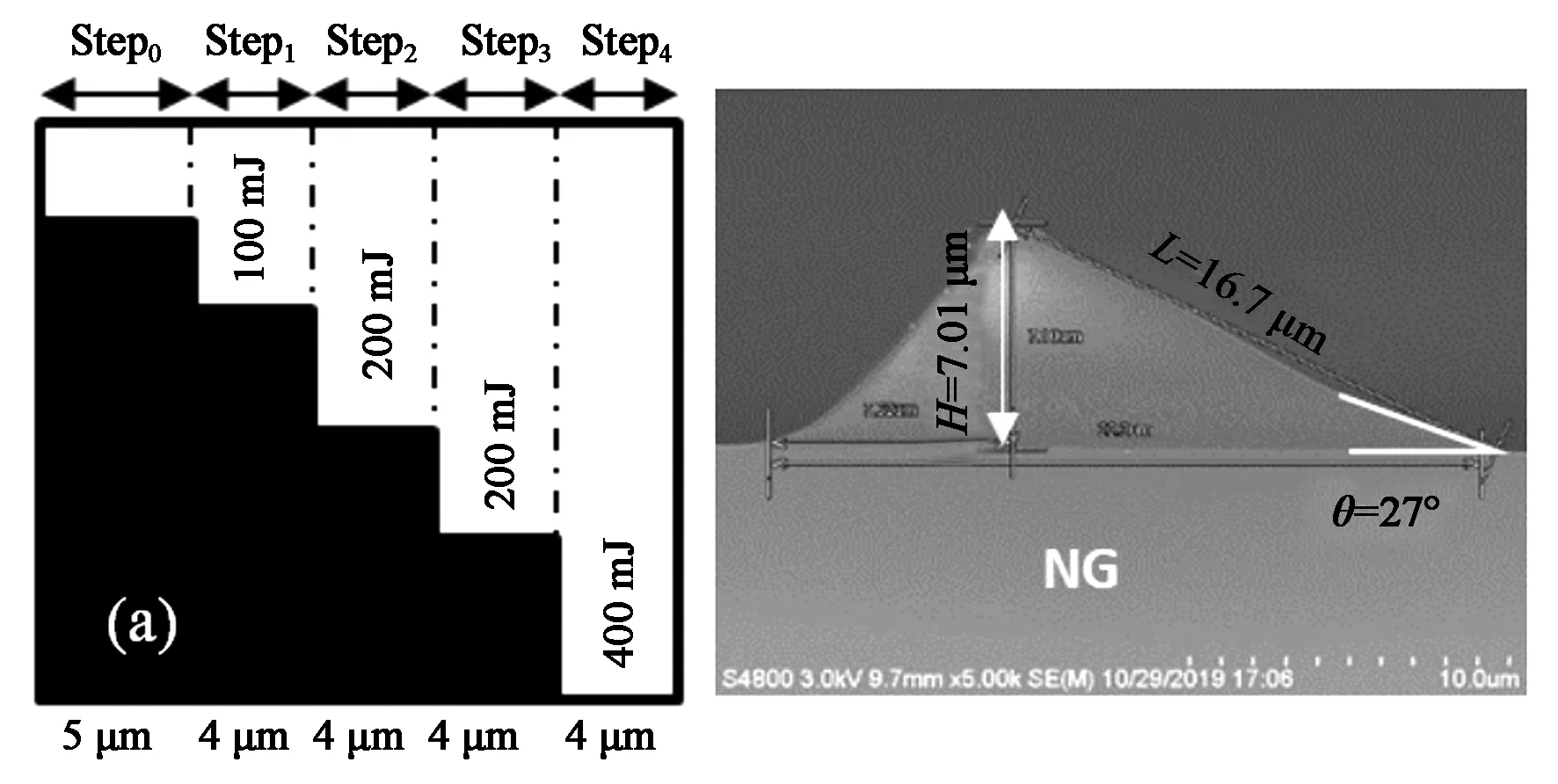
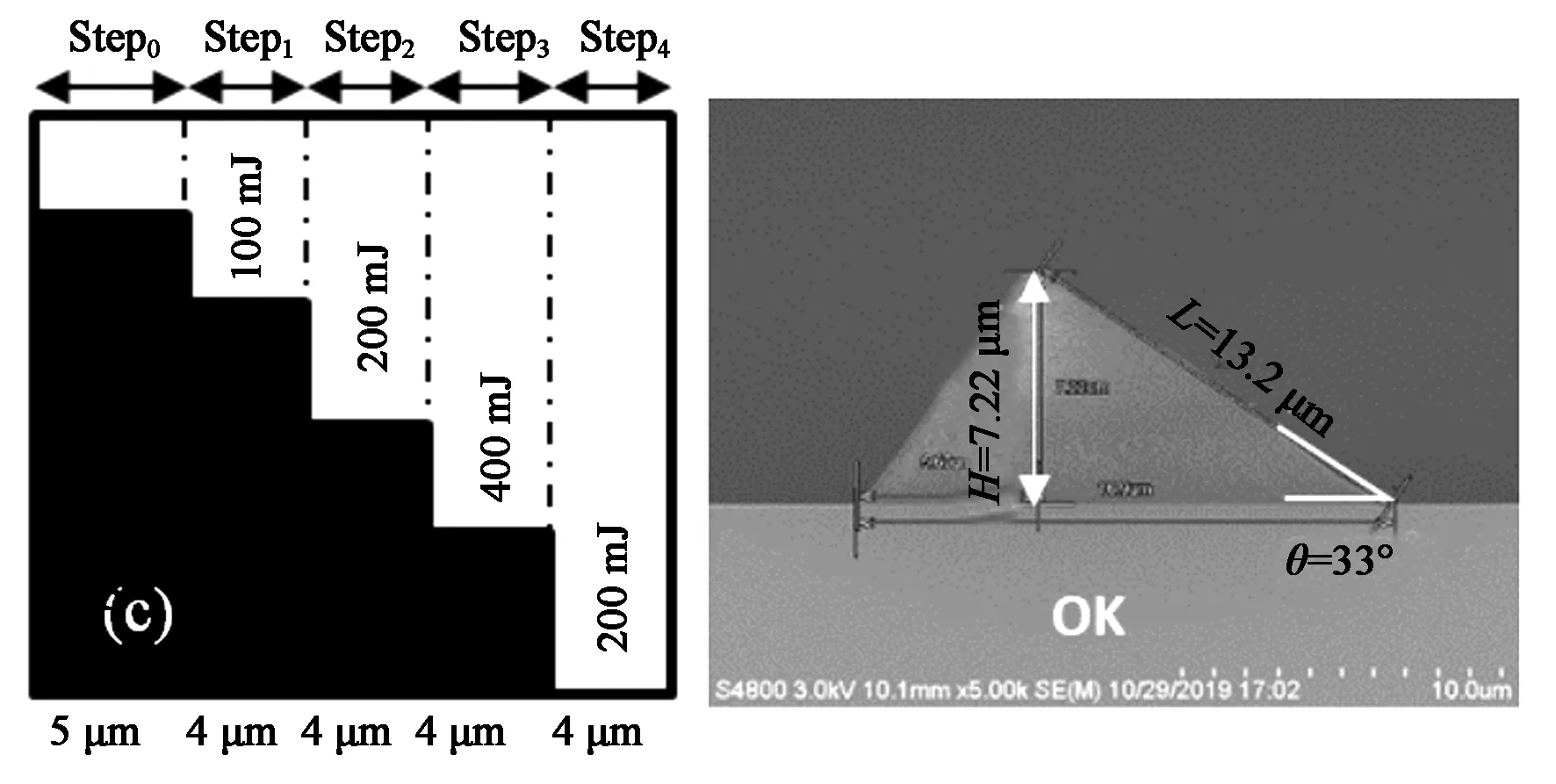
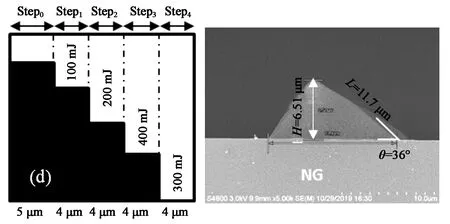
圖6 不同曝光條件(左)得到的相應楔形光阻形貌(右)(H=7.5 μm)。(a) Step3=200 mJ，Step4=400 mJ；(b) Step3=300 mJ，Step4=300 mJ；(c) Step3=400 mJ，Step4=200 mJ；(d) Step3=400 mJ，Step4=300 mJ。Fig.6 Wedge-shaped photoresist profile obtained under different exposure conditions (H=7.5 μm). Images on the left represent the exposure condition. (a) Step3=200 mJ, Step4=400 mJ； (b) Step3=300 mJ, Step4=300 mJ； (c) Step3=400 mJ, Step4=200 mJ； (d) Step3=400 mJ, Step4=300 mJ.

圖7為制作的單色指向式顯示器件不同視角的效果圖，目標視角為30°。從顯示效果可以看出，視角小于或大于30°時，屏幕的亮度均有所降低，說明采用錯位疊加曝光方法制作的斜面微結構可以有效地實現背光的特定角度反射。

圖7 指向式顯示器件不同視角的顯示效果Fig.7 Display effects from different perspectives

5 結 論

本文基于UV感光的T公司生產的某正性光阻，采用錯位疊加曝光的方法，實現了同灰階曝光技術相同的效果，建立了獲得特性角度的楔形斜面結構的理想模型以及等效模型，并通過實驗在Lambert-beer定律的基礎上計算出該型號正性光阻感光前后的不同吸收系數α與α′，以及使該光阻發生光化學反應的臨界能量，最后通過實驗制作出與理論設計匹配的楔形斜面結構的光阻結構。

實驗結果證明：該型光阻在感光前與感光后對UV的吸收系數不同，感光前的吸收系數α約為1.14，而感光后的吸收系數α′約為感光前的20%。使該型光阻發生光化學反應的臨界UV能量約為8 mJ，低于該能量值時光阻幾乎不發生反應。基于錯位疊加曝光的方法，將具有特定角度及高度的楔形斜面結構等效為臺階狀結構后，并根據Lambert-beer定律計算得到的錯位曝光能量，可以得到與理論設計相同的楔形斜面結構。