超大跨度公鐵兩用懸索橋活載剛度研究

許磊平 霍學晉

（中鐵大橋勘測設計院集團有限公司，武漢 430050）

由于跨江橋位資源寶貴，同時搭載多種交通功能的橋梁更受建設方的青睞，超大跨度公鐵兩用懸索橋往往是較優方案［1-3］。此類橋梁計算理論復雜，設計難度大，主要表現為：超大跨度橋——屬于柔性結構，需采用幾何非線性（下文簡稱非線性）分析理論計算；公鐵兩用橋——同時搭載公路、鐵路，設計活載往往比單一功能橋梁大很多。結構方案比選的重要指標是活載剛度，且活載效應受各構件共同影響。當跨度超過千米后，需對影響結構活載剛度的各項因素進行參數研究。

國外學者對非線性理論研究較早，多采用撓度理論。Wollmann［4］基于撓度理論建立了一種用于求解非線性效應的實用解法；Clemente 等［5］利用撓度理論分析了大跨度懸索橋設計參數對結構力學性能的影響，發現隨著跨度的增加，懸索橋受力特性逐漸趨近單根主纜的力學特性；Jennings［6］忽略活載對主纜內力的影響，對集中荷載及均布荷載作用下公鐵兩用懸索橋主纜變形特征進行了研究，發現活載較大時，若直接忽略活載對成橋內力的影響會存在一定的偏差。國內學者在此基礎上，將非線性理論應用到懸索橋上，并對其特有的問題開展了一系列研究。沈銳利等［7］對懸索橋開展了靜動力空間非線性計算有限元模型的研究工作，并應用到實際工程中；唐茂林等［8］提出了懸索橋成橋主纜線形計算的分段懸鏈線法，求解精度大大提高；柴生波等［9］研究了懸索橋橋塔頂位移、主纜的彈性伸長及不平衡均布活載作用下的主纜變形特性。

為了提高列車通過鐵路橋梁時的行車安全性及舒適性，橋梁剛度需滿足一定的要求。TB 10002—2017《鐵路橋涵設計規范》［10］對鐵路橋梁剛度提出了限制性要求，主要對梁體的撓跨比、橫向變形、梁端轉角等指標進行了限制。然而該規范僅適用于跨度不大于168 m 的鋼梁、跨度不大于128 m 的混凝土梁和墩高不大于50 m的橋梁。

本文以實際工程為背景，采用中鐵大橋院自主研發的大跨度懸索橋非線性計算分析軟件SNAS 開展研究工作，建立基于全量法的非線性和混凝土收縮徐變的耦合算法，采用完全非線性算法求解活載。基于超大跨度公鐵兩用懸索橋成橋線形，以找形結果為基礎，建立懸索橋精細化有限元模型，對活載作用下懸索橋的非線性效應、矢跨比、主塔剛度、邊纜跨度、邊跨加勁梁梁長等進行詳細分析，研究不同參數對懸索橋活載剛度的影響規律。

1 工程概況

一座跨越長江的公鐵兩用懸索橋，橋址區主通航孔較寬。為不影響通航，采用超大主跨懸索橋跨越主通航孔。綜合比選設計中滿足通航需求的多個結構方案，選取主跨1560 m 超大跨度懸索橋方案進行研究，孔跨布置為（2×120+1560+2×120）m，如圖1所示。

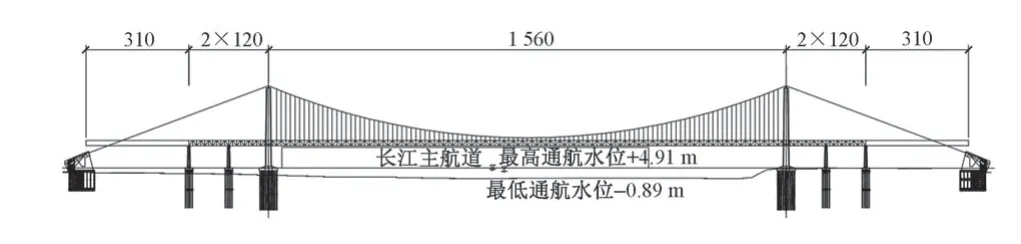
圖1 結構方案（單位：m）

為節約橋位資源，該橋同時搭載高速公路、高速鐵路和客貨共線鐵路。加勁梁采用鋼桁梁斷面（圖2），上下雙層布置。上層橋面為雙向八車道高速公路，設計速度100 km/h。下層橋面上游側為雙線高速鐵路，設計速度350 km/h，到發線有效長度650 m；下游側為雙線普通鐵路，設計速度160 km/h。

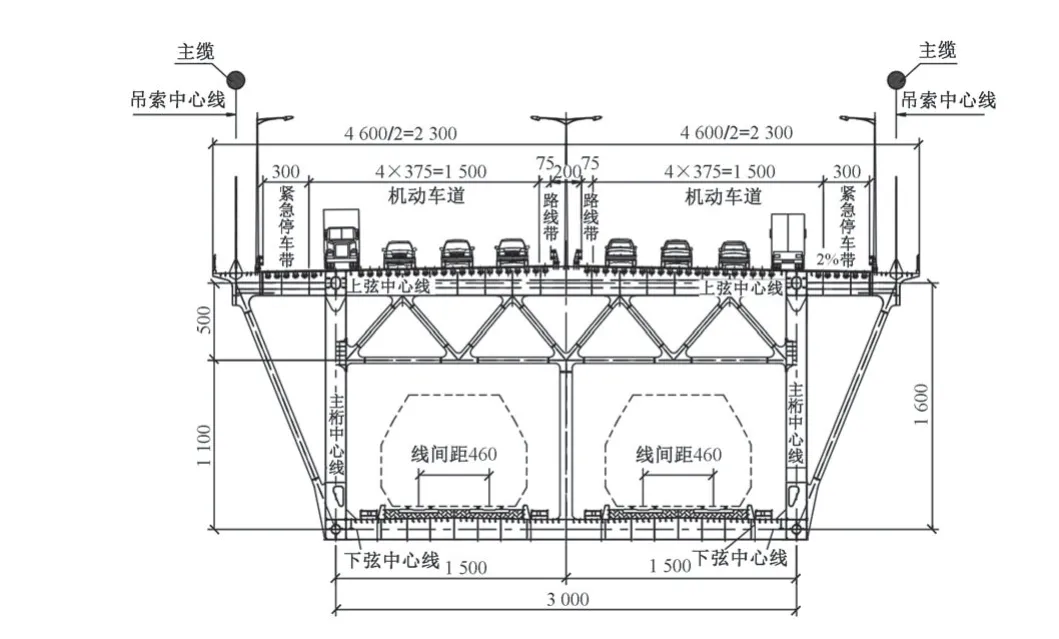
圖2 主梁橫斷面（單位：cm）

2 成橋狀態確定

懸索橋成橋狀態的計算是開展運營階段分析的基礎。懸索橋的成橋線形是指在結構恒載（一期恒載與二期恒載）作用下，懸索橋逐階段施工至竣工時刻在設計基準溫度下的結構線形。本文基于精確懸鏈線理論確定成橋狀態下主纜和吊桿的無應力長度，更新懸索橋有限元模型并開展參數敏感性分析。

在SNAS 中建立全橋空間有限元模型。主纜和吊桿采用空間索單元模擬，主塔和加勁梁采用空間梁單元模擬；主塔底固結，主纜在錨碇位置固結，采用主從連接模擬支座以及纜塔間的連接。

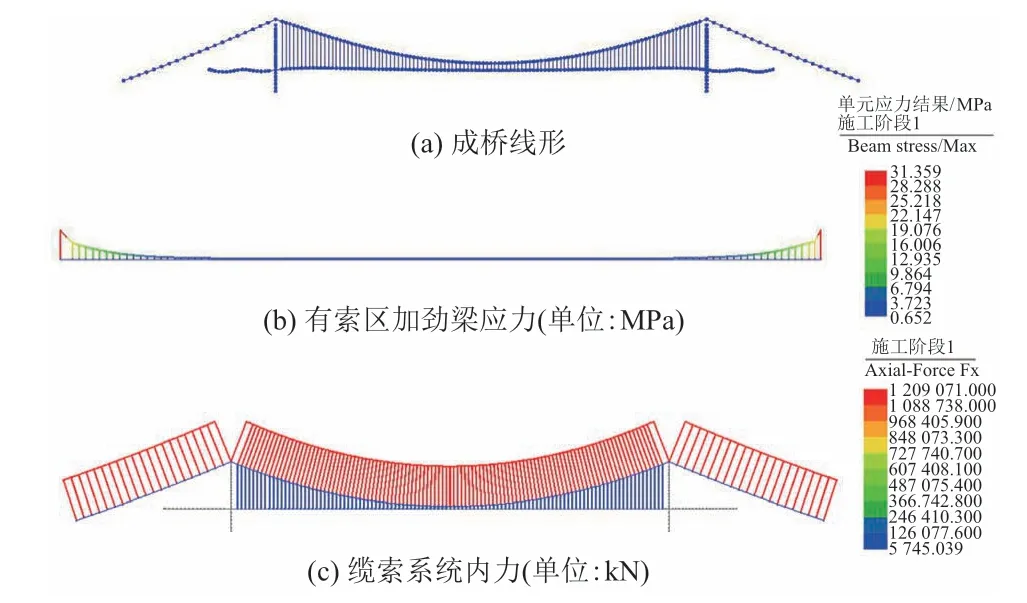
圖3 成橋狀態

成橋狀態見圖3。可知，中跨加勁梁最大變形為3.6 cm，線形較好；有索區鋼梁最大應力31.4 MPa，應力較低；主纜和吊桿的軸力分布均勻，可作為進一步分析的基準狀態。

3 活載剛度研究

上層橋面高速公路采用公路一級荷載，按照車道數和跨度進行橫向多車道折減和縱向折減；下層橋面雙線高速鐵路選取ZK 活載；雙線普通鐵路采用中-活載。根據到發線長度650 m 并考慮安全距離，ZK 活載和中-活載分別采用550，970 m 定長加載。重點研究懸索橋的撓跨比、梁端轉角及梁端縱向位移3 個總體剛度指標。

3.1 活載非線性影響

對于超大跨度公鐵兩用懸索橋，活載產生的結構內力和變形是重點設計內容。為了節約計算時間，懸索橋活載效應通常采用線性理論計算。隨著懸索橋跨度的增大，活載的非線性效應愈發顯著。非線性對活載效應的影響程度應通過數值分析確定。為此，對主跨1560 m 懸索橋分別采用線性及非線性2 種方法分析其活載效應，剛度指標見表1。以線性分析結果為基數1，將非線性分析結果與其作商，見圖4。

表1 線性和非線性分析剛度指標

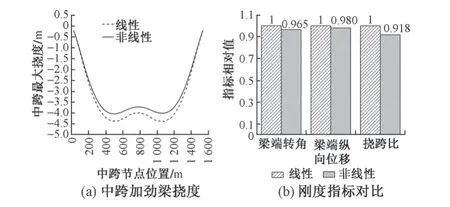
圖4 線性和非線性分析結果對比

由表1 和圖4 可知：①超大跨度懸索橋在活載作用下的變形呈W 形，2 種分析方法得到的2 個極值點均出現在約L/4 和3L/4 處（L為主跨跨度）。②線性分析方法及非線性分析方法得到的活載撓度最大值分別為4.402，4.040 m。由于非線性分析方法精確，可認為采用線性方法分析該橋的活載撓度比實際值偏大8.96%。③梁端轉角對行車性能影響較大，采用2種分析方法得到的梁端轉角相差較小，梁端縱向位移接近。

綜上，采用線性方法分析橋梁活載、加勁梁撓度、梁端轉角及梁端縱向位移均被高估，從經濟性方面考慮，建議采用非線性方法。

3.2 矢跨比影響

矢跨比對結構的受力性能具有重要的影響。因此，分析矢跨比分別為1/9，1/10，1/11 時懸索橋的受力規律。矢跨比敏感性分析結果見表2。以矢跨比為1/10 時的分析結果作為基數1，將不同矢跨比的分析結果與其作商進行矢跨比影響分析，見圖5。

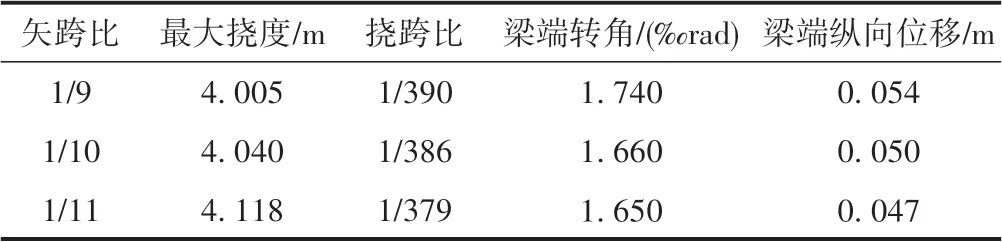
表2 矢跨比敏感性分析結果

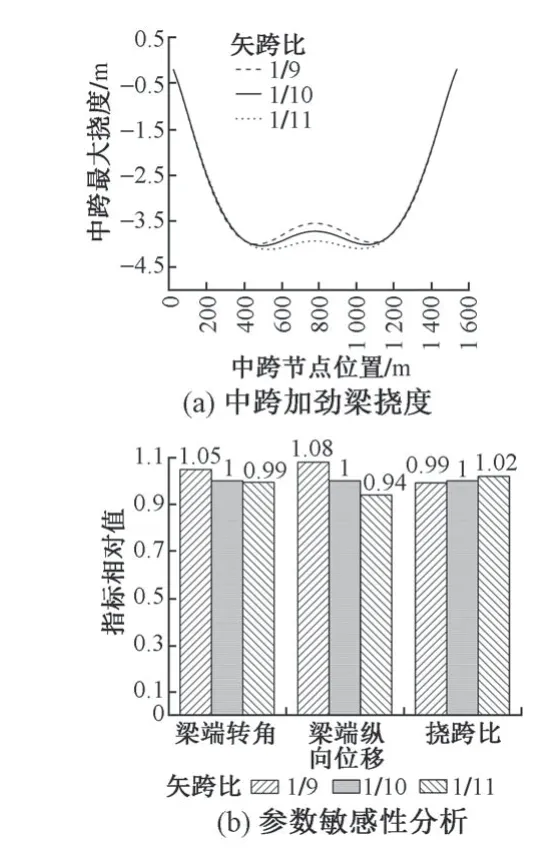
圖5 矢跨比影響分析

由表2 和圖5 可知，①隨著矢跨比的減小，梁端轉角逐漸減小，說明增加主跨跨度改善了橋梁的行車性能。②梁端縱向位移逐漸減小。對大跨度橋梁而言，溫度和活載引起的梁端縱向位移大，設置梁端伸縮裝置困難，且大位移量的伸縮裝置是鐵路橋梁構造的薄弱點。因此，減小矢跨比可以降低梁端伸縮裝置的設置難度。③主跨撓跨比逐漸增加，說明結構剛度降低。因此，適當提高矢跨比可降低跨中撓度。目前，規范僅針對小跨度橋梁的撓跨比有規定，對超大跨度懸索橋尚無明確規定。

3.3 主塔剛度影響

懸索橋屬纜索體系橋梁，結構的剛度由主纜、吊索、主塔、加勁梁等構件共同提供。超大跨度懸索橋的主塔較高，主塔截面的選取需要同時考慮強度和剛度要求。以主塔設計剛度為基數1，通過調整主塔剛度倍數（表3）來分析主塔剛度對結構總體剛度的影響，見圖6。

由表3 和圖6 可知：①隨著主塔剛度的提高，梁端轉角變化十分微小，說明提高主塔剛度對邊跨加勁梁端轉角的改善作用極小；②梁端縱向位移從0.050 m逐漸降低到0.038 m，說明提高主塔剛度可有效降低梁端伸縮量；③主跨撓跨比從1/386 降低到1/399，結構剛度略有改善，但效果不明顯。

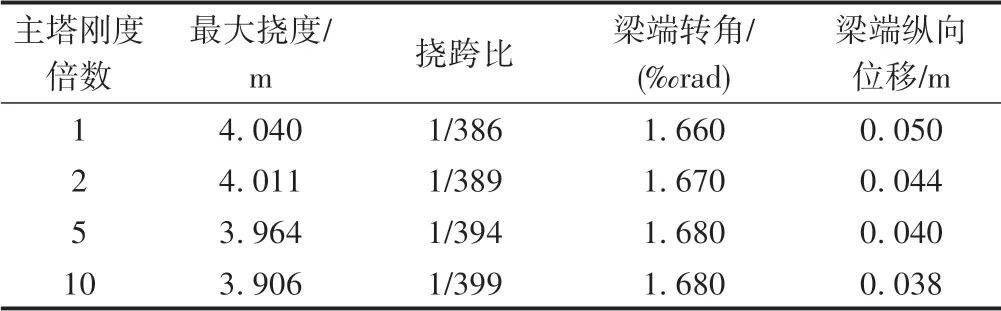
表3 主塔剛度敏感性分析結果

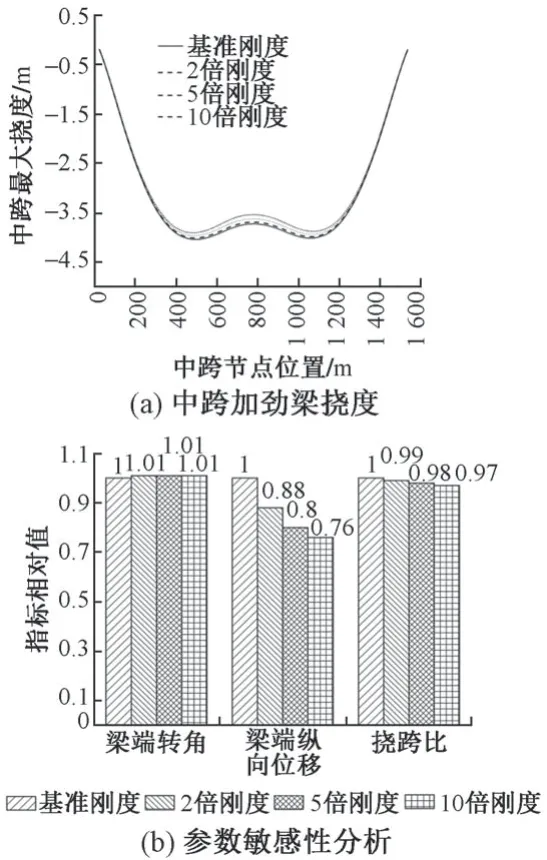
圖6 主塔剛度影響分析

本文分析主塔剛度對懸索橋總體剛度的影響時沒有考慮鞍座抗滑問題，設計中應綜合考慮主塔剛度對結構總體剛度及鞍座抗滑的影響并進行優化。

3.4 邊跨主纜跨度影響

邊跨主纜為中跨提供錨固作用，錨固作用的強弱與邊跨主纜跨度（邊跨主纜沿水平投影長度）有一定的關系。因此，分析邊跨主纜跨度分別為350，550，750 m 時結構的剛度變化規律，邊跨主纜跨度敏感性分析結果見表4。以邊纜550 m 跨度的分析結果作為基數1，將不同邊跨主纜跨度的分析結果與其作商進行矢跨比影響分析，見圖7。

表4 邊跨主纜跨度敏感性分析結果

由表4 和圖7 可知：①隨著邊跨主纜跨度的增加，梁端轉角略有增加，說明提高邊跨主纜跨度對梁端轉角的改善作用不明顯；②梁端縱向位移從0.048 m 逐漸增加到0.053 m，說明邊跨主纜跨度的增加不利于梁端伸縮裝置的設置；③主跨撓跨比從1/400 增大到1/364，說明邊跨跨度越大，邊跨主纜的錨固作用越弱，因而跨中撓度增加。

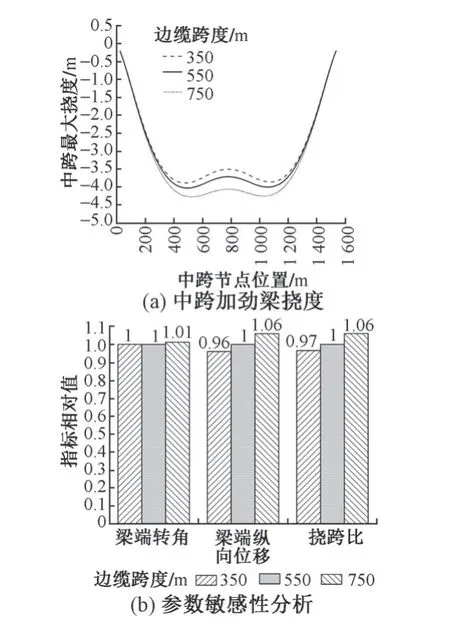
圖7 邊跨主纜跨度影響分析

3.5 邊跨加勁梁長度影響

分析邊跨加勁梁長度分別為2×60 m，2×120 m，2×180 m 時結構剛度的變化規律，其敏感性分析結果見表5。以邊跨加勁梁長度為2 × 120 m 時的分析結果作為基數1，將不同邊跨加勁梁長度的分析結果與其作商進行邊跨加勁梁長度影響分析，見圖8。

表5 邊跨加勁梁長度敏感性分析結果

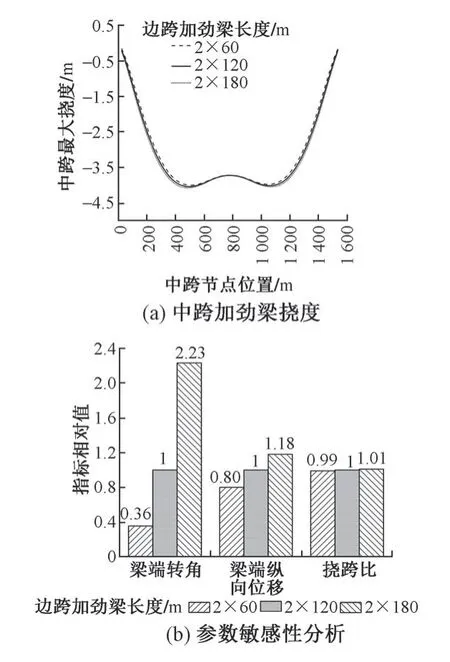
圖8 邊跨加勁梁長度影響分析

由表5 和圖8 可知：①隨著邊跨加勁梁長度的增加，梁端轉角顯著增加，這是因為邊跨梁端轉角受結構自重影響較大，且受跨度影響十分明顯；②梁端縱向位移從0.040 m逐漸增加到0.059 m，增加了梁端伸縮裝置的設置難度；③主跨撓跨比從1/390 增大到1/383，說明結構剛度有所降低，但變化較小。

4 結論

1）超大跨度公鐵兩用懸索橋采用懸鏈線理論確定其成橋線形具有較高的精度，滿足精度要求。

2）基于線性方法得到的活載效應比非線性方法的數值偏大。從設計方面和經濟性考慮，超大跨度懸索橋應選取非線性方法分析活載效應。

3）公鐵兩用懸索橋在活載作用下的變形受多個參數的影響。適當減小矢跨比，可降低梁端縱向變形及梁端轉角；提高主塔剛度可顯著降低梁端縱向變形；減小邊跨主纜跨度可增強其錨固作用，提高結構剛度；不同的邊跨加勁梁長度對梁端轉角及梁端縱向變形具有較大影響，而對撓跨比影響小。