傅里葉變換的“4+2”教學方法

許 可， 陳沛鉑， 王 玲， 鄧 彬， 萬建偉

(國防科技大學 電子科學學院，湖南 長沙 410073)

0 引言

在電子信息類本科專業中，“數字信號處理”是一門開設在“信號與系統”[4]課程之后的專業基礎課程[1～3]。但是在“數字信號處理”課程的教學實踐中，我們發現學生往往對前修課程的相關知識點產生了混淆或遺忘，比如學生認為之前已經學過了連續時間傅里葉變換和離散時間傅里葉變換，接下來還會學習離散傅里葉變換，不知道這些“傅里葉”是什么關系？大名鼎鼎的FFT(Fast Fourier Transform)算法，將數字信號處理從理論研究推向了工程實踐，那么FFT算法是一種全新的傅里葉變換嗎？

為了更好地銜接學科基礎課(“信號與系統”)和專業基礎課(“數字信號處理”)的相關知識點，我們采取“4+2”教學方法來歸納這兩門課程中涉及到的六種傅里葉變換[1,5](如表1所示)。

“4”是指在“信號與系統”課程中學習過的4種傅里葉變換，即CTFS，CTFT，DTFS和DTFT。在時域和頻域，這些“傅里葉”或者是連續的，或者是無限長的，因此不方便用計算機或DSP(Digital Signal Processor)直接處理。

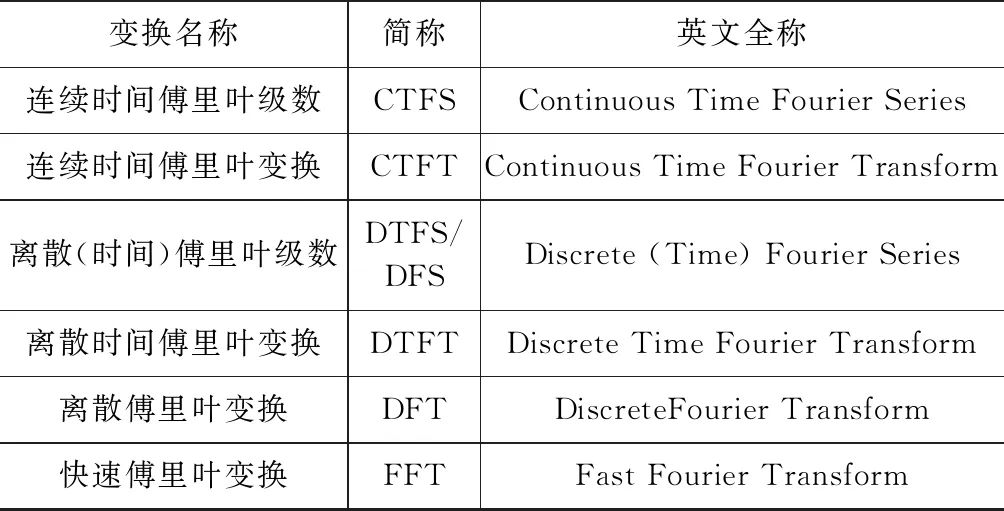
表1 六種傅里葉變換

“2”是指在“數字信號處理”課程中將要學習的2種傅里葉變換，即DFT和FFT。在時域和頻域，這兩個“傅里葉”都是離散且有限長的，因此可以用計算機或DSP直接處理。

因此，能否通過計算機或DSP直接處理，可以作為劃分“信號與系統”與“數字信號處理”這兩門課程知識點的一個準則，也是把這六種傅里葉變換劃分為“4+2”的原因[1,5]。

在課程教學中還需要特別指出：DFS是DTFS的簡稱，但DFT不是DTFT的簡稱，這算一種約定俗成。因此在有的教材中為了同DFT區分開，特意把DTFT稱作“離散時間序列的傅里葉變換”[1,2]。

1 “信號與系統”中的“傅里葉”

可以用三角波和周期三角波為講解對象(見圖1)，復習和歸納“信號與系統”課程中講授的四種傅里葉級數變換。在此的“傅里葉變換”是一種廣義的說法，也就是說無論是“傅里葉變換(Fourier Transform)”，還是“傅里葉級數(Fourier Series)”，統稱“傅里葉變換”。

圖1左側表示時域，右側表示頻域。在時域，橫軸表示從連續時間信號到離散時間信號，兩者的轉換就是采樣；縱軸表示從周期信號到非周期信號，兩者的轉換就是將周期趨向于無窮大。在頻域也有類似的轉換關系，需要注意的是，時域和頻域的坐標定義與方向是不同的。

為了全面理解圖1的內涵，需要深刻理解下面兩句話[1,6,7]：

第一句話，傅里葉變換是時域到頻域的橋梁。

可以看出這四種傅里葉變換都是從左(時域)到右(頻域)的箭頭，起到了時域到頻域的橋梁作用。反過來，從頻域到時域也有橋梁，這就是對應的各種傅里葉反變換。

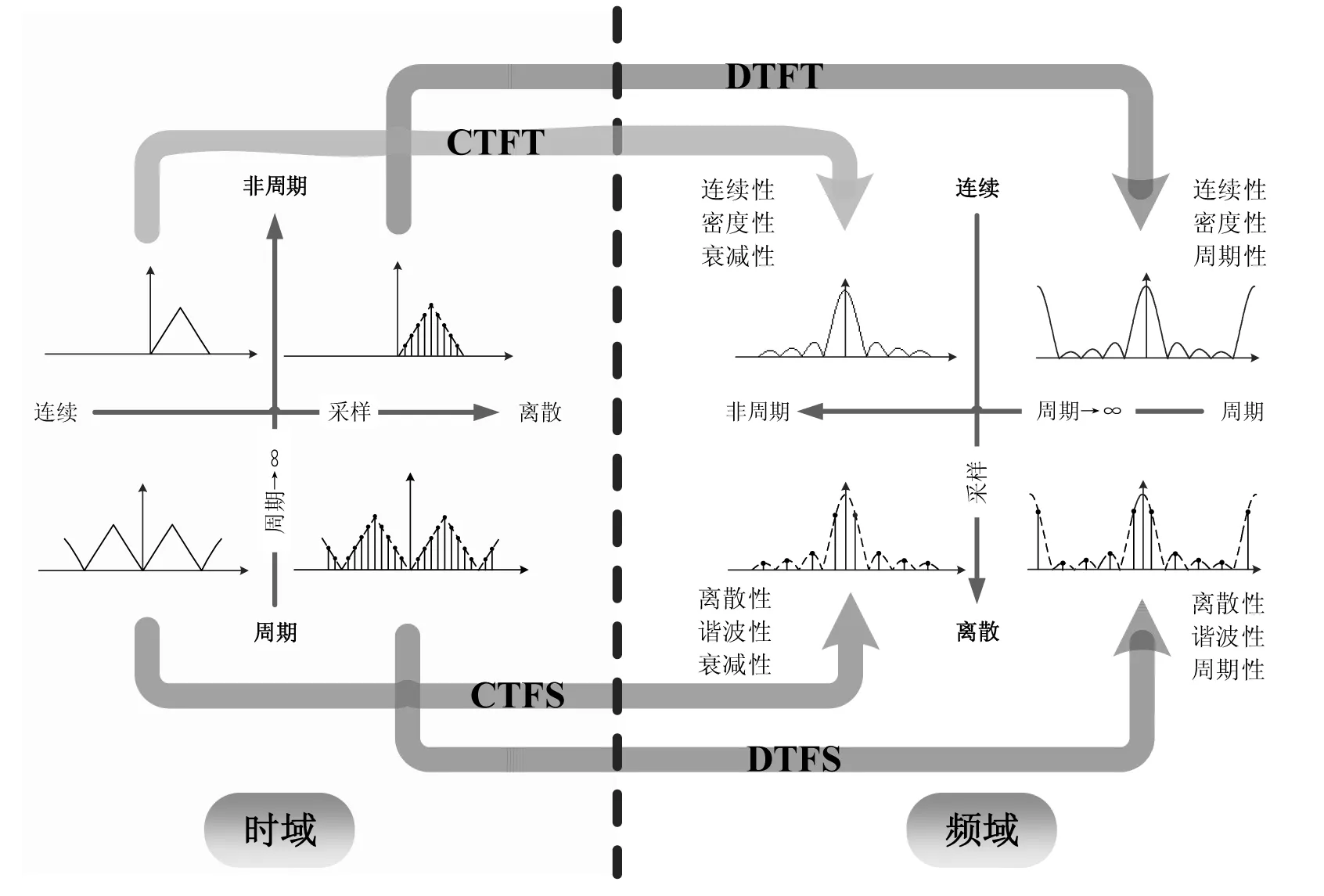
圖1 四種傅里葉變換的關系

第二句話，一個域的離散，對應另外一個域的周期延拓。對于這句話，最耳熟能詳的就是時域采樣定理中的“時域采樣對應頻域上的周期延拓”，結合圖2，我們還可以更全面的理解這句話：①時域上的離散(采樣)，對應頻域上的周期延拓，即序列的DTFT和周期序列的DTFS，兩者在頻域上都呈周期特性。②時域上的連續，對應頻域上的非周期，即非周期信號的CTFT和周期信號的CTFS。③時域上的周期，對應頻域上的離散，離散的頻域取值就稱作傅里葉級數，即周期信號的CTFS和周期序列的DTFS。④時域上的非周期，對應頻域上的連續，連續的頻域取值就稱作傅里葉變換，即非周期信號的CTFT和序列的DTFT。

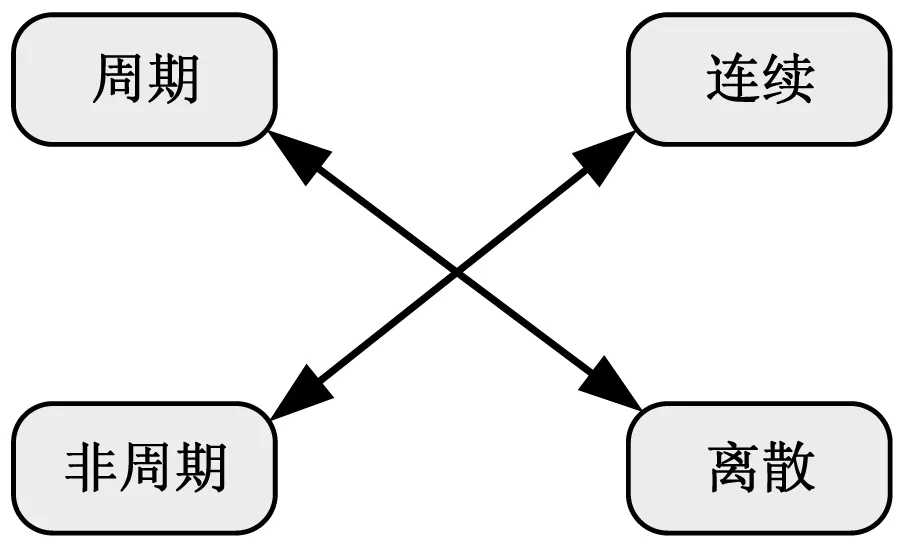
圖2 “周期-離散，非周期-連續”的對應關系

2 “數字信號處理”中的“傅里葉”

“數字信號處理”課程中將要學習兩種“傅里葉”，分別是DFT和FFT。無論是在時域還是頻域，DFT/FFT所處理的信號都是離散且有限長的，這才是能用計算機或DSP直接處理的根本原因。需要特別強調的是：FFT只能算作一種“加速版”的DFT，它不是一種新的傅里葉變換。

對模擬信號經A/D采樣并進行截斷(加窗)處理，成為有限長的時域離散數據，但在頻域其頻譜仍然是連續且周期的(DTFT)，計算機或DSP此時仍然不方便直接處理。此時，我們采取“三橫兩縱”的關系圖來理解有限長序列DFT的推導過程[1](見圖3)。

“三橫”指三種變換關系，即DTFT、DFS和DFT。仍然可用“傅里葉變換是時域到頻域的橋梁”，以及“一個域的離散對應另外一個域的周期延拓”這兩句話來深刻理解這三種變換關系。并且這三種變換的“進化”過程可以輔助理解DFT的周期特性是如何被“隱藏”起來的。

“兩縱”指在時、頻兩個域同時進行的操作。在時域經過了“均勻采樣→周期延拓→取主值序列”操作，對應于在頻域進行的“周期延拓→均勻采樣→取主值序列”操作。通過DFT變換，從時域的N點樣本序列出發，得到頻域的N點樣本序列。

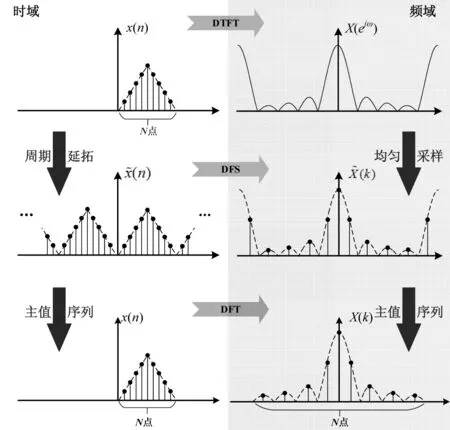
圖3 DFT與其它變換關系示意圖(“三橫兩縱”)

3 結語

在“數字信號處理”課程的教學實踐中，通過圖表法來總結歸納前后課程知識點，可以起到事半功倍的作用。我們一般在第2次課就會結合圖2來復習前修課程的知識點，學生反映他們可以思路清晰、自信滿滿的開始專業課程的學習。結合圖3來講授DFT，學生不僅可以完整的理解DFT的來龍去脈，而且還更深刻的理解了DFT隱含的周期特性。