磁性斯格明子的旋性布朗運動研究

趙 樂，江萬軍

(清華大學 物理系，北京 100084)

磁性斯格明子是一種具有粒子特性的非共線自旋結構. 由于其拓撲屬性的存在，許多新奇的拓撲量子輸運現象，譬如拓撲霍爾效應、斯格明子霍爾效應等在斯格明子材料體系中都得到了廣泛研究. 布朗運動是一種十分普遍的非平衡態熱動力學現象，它描述的是熱擾動下浸潤在液體中微小顆粒的隨機運動行為. 作為一種準粒子，磁性斯格明子在溫度漲落時，同樣會表現出隨機運動的特性，但與其拓撲屬性相關的熱動力學行為卻一直沒有被發現. 本文介紹了實驗室中對斯格明子熱動力學行為的研究方法以及清華大學物理系江萬軍課題組近期在這一方向的研究進展，希望能夠激發學生對于自旋電子學領域的研究興趣，并為相關方向的研究提供一些方法與思路.

1 背景介紹與研究現狀

1.1 布朗運動行為

布朗運動是指懸浮在流體(液體或氣體)中的粒子在高速運動流體分子的碰撞下呈現出的隨機運動行為(圖1)，最早由蘇格蘭物理學家Robert Brown利用光學顯微鏡觀察到，相關研究結果發表于1828年的《哲學》雜志上[1]. 1905年，根據分子動力學理論和擴散方程，愛因斯坦給出了布朗運動顆粒均方位移(Mean-squared Displacement,MSD)的表達式[2]

MSD(t*)=2dDdct*,

其中，d為運動的維數，Ddc為顆粒的擴散系數，t*

為用于計算MSD的統計間隔時間. 愛因斯坦還進一步指出，擴散系數Ddc應該是溫度的線性函數，有

Ddc=μkBT,

其中，μ為顆粒的遷移率，kB為玻爾茲曼常量，T為熱力學溫度. 此關系式也得到了后續大量實驗的驗證.

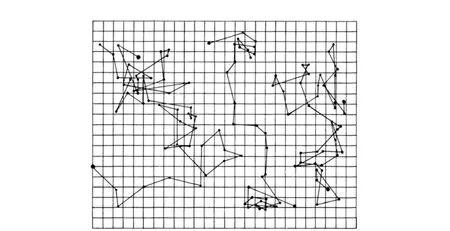
圖1 布朗運動顆粒的隨機運動軌跡圖[3]

1.2 磁性斯格明子

斯格明子(Skyrmion)一詞來源于英國核物理學家Tony Skyrme于1962年在粒子物理領域提出的一種類似于獨立粒子的拓撲穩定場結構[4]. 2009年德國慕尼黑工業大學Peter B?ni課題組利用小角中子散射的方法在MnSi單晶塊體材料中首次觀測到了這種受拓撲保護的局域螺旋磁性結構[5]. 研究發現，相對于磁疇、磁泡等傳統磁性結構，磁性斯格明子具有尺寸小、穩定性高、易于被電流操控等優點，因而引起了人們的高度關注與深入研究.

磁性斯格明子的拓撲屬性是可以由拓撲電荷數來描述的，其表達式為

其中m為局域磁化強度方向上的單位矢量. 由于Q為m的奇函數，因此通過外加磁場，就可以改變磁化強度的方向，進而得到Q=+1和Q=-1的斯格明子(圖2). 磁性斯格明子的拓撲電荷數始終為整數，而外界環境需要提供較多能量才可以破壞斯格明子的整體結構，這便是斯格明子拓撲保護的來源.

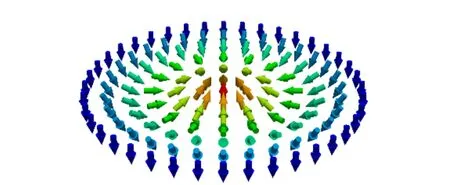
(a)Q=+1

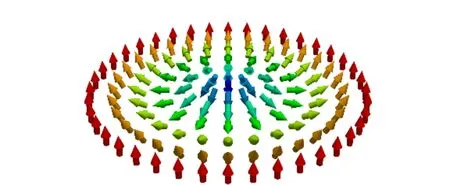
(b)Q=-1圖2 重金屬-磁性薄膜材料體系中Q=+1與Q=-1奈爾型斯格明子示意圖

拓撲電荷數相反(Q=±1)的磁性斯格明子在輸運測量中會展現出相反的動力學行為，斯格明子霍爾效應就是其中非常典型的例子[6]. 如圖3所示，在Ta/CoFeB/TaOx磁性多層膜中，通過施加橫向(-x)方向的電流，利用磁光克爾效應顯微鏡成像技術，可以觀測到Q=-1和Q=+1的斯格明子分別在縱向(-y與+y方向)發生偏轉和堆積. 這種現象與電子和空穴的霍爾效應非常相似.

(a)Q=-1

(b)Q=+1圖3 利用磁光克爾效應顯微鏡直接觀察到磁性斯格明子的霍爾效應現象

1.3 磁性斯格明子熱動力學行為的研究情況

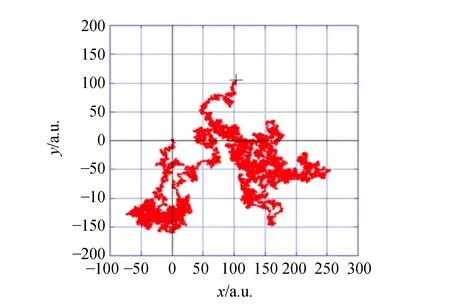
(a)數值模擬

(b)實驗觀測圖4 數值模擬與實驗觀測得到的磁性斯格明子布朗運動軌跡圖

磁性斯格明子熱動力學的早期研究集中在理論推導與數值模擬方面[圖4(a)][7-10]. 2019年，日本大阪大學Takayuki Nozaki等率先在W/FeB/Ir/MgO多層膜中觀測到斯格明子在熱擾動下的隨機運動現象，并研究了垂直方向電場對斯格明子擴散系數的影響[11]. 德國美因茨大學Mathias Kl?ui課題組也隨后研究了Ta/CoFeB/Ta/MgO/Ta體系中斯格明子的布朗運動行為，以及斯格明子擴散系數隨溫度的非線性變化關系[圖4(b)][12]. 他們還指出，利用斯格明子的隨機布朗運動行為，可以用來構建非常規計算單元. 但這些前期研究并沒有就斯格明子的拓撲屬性在熱動力學行為中的表象進行深入討論.

2 實驗方法與研究思路

2.1 使用磁光克爾效應顯微鏡觀察磁性斯格明子

磁光克爾效應(Magneto-optic Kerr Effect)是由蘇格蘭物理學家John Kerr于1877年發現的[13]，當1束線偏振光入射到磁化強度不為零的磁性樣品表面并發生反射時，由于磁性樣品對入射光p分量和s分量的反射率存在差異，故反射光的偏振方向會相對入射光轉過一定角度，因此通過測量反射光偏振方向的改變就可以獲知樣品表面的磁矩指向.

利用磁光克爾效應顯微鏡，可以對樣品表面不同位置的磁性信號進行實時觀測，實現磁結構的空間分辨. 以德國Evico Magnetics公司生產的磁光克爾效應顯微鏡系統為例，該系統主要由光學顯微鏡、電磁鐵、恒流源、樣品托、LED燈組、CMOS相機和計算機等部分組成，系統光路圖如圖5所示. LED燈光通過光纖導入光學系統，在經過透鏡組與光闌調制后，經過起偏器變為線偏振光并聚焦入射于樣品表面，反射光在經過補償器和檢偏器后即可使用目鏡進行觀察或利用CMOS相機捕獲并傳輸至計算機. 使用相配套的KerrLab控制與采集程序可以實現每秒近30幀的視頻錄制，這為研究磁性斯格明子的動力學提供了途徑.

圖5 Evico Magnetics公司生產的磁光克爾效應顯微鏡成像光路示意圖[14]

2.2 利用ImageJ軟件獲取磁性斯格明子的位置信息

利用ImageJ軟件可以對使用KerrLab程序錄制的視頻進行后期處理與分析. ImageJ是基于Java的多平臺公共圖像處理軟件[15]，擁有大量官方和第三方插件，為基于圖片分析的科學研究提供了極大方便. 本研究中，利用由M.B. Smith等開發的Speckle TrackerJ插件[16]，對視頻中的運動物體進行自動追蹤并獲取物體在每幀圖片上的坐標信息，同時將數據導出為文本文件進行后續計算和處理. 如圖6所示，首先使用ImageJ對采集到的原始視頻圖像進行反色與提高對比度操作，接下來進行高斯模糊，可以發現圖像中的背景噪聲被基本消除，且斯格明子圖像邊緣平滑、辨識度增強. 最后使用Speckle TrackerJ插件對斯格明子位置進行追蹤，即可得到其隨時間變化的位置數據.

(a)原始圖像

(b)進行反色、提高對比度

(c)高斯模糊圖6 使用ImageJ軟件對圖像進行處理

2.3 計算均方位移與擴散系數

通過計算均方位移，可以非常直觀地反映熱運動顆粒的擴散行為. 對于二維運動，均方位移的表達式為

MSD(t*)=〈Δr2(t*)〉=

〈Δx2(t*)+Δy2(t*)〉=

[y(iΔt+t*)-y(iΔt)]2}=4Ddct*,

其中，Δt為位置數據的時間分辨率，t*為統計間隔時間，即對于不同的統計間隔時間會得到不同的均方位移. 理論上均方位移與統計間隔時間之間滿足較好的線性關系，通過線性擬合得到斜率即可計算出運動顆粒擴散系數Ddc的大小.

3 實驗進展

3.1 觀察單個磁性斯格明子的隨機熱運動行為

首先使用超高真空磁控濺射設備生長了具有磁性斯格明子的Ta(5 nm)/Co20Fe60B20(1 nm)/TaOx(3 nm)3層膜結構[17]. 為了消除各向異性形狀限制的影響，進一步使用微加工技術將樣品制備為圓形器件，如圖7所示. 接下來使用磁光克爾效應顯微鏡觀察樣品表面的磁疇結構，在略高于室溫的環境中(320.6 K)，可以觀察到單個斯格明子受到熱擾動而呈現出隨機運動的行為. 錄制視頻并使用ImageJ進行處理，即可得到單個斯格明子的運動軌跡圖，如圖8(a)所示. 利用不同時刻的位置數據，可以計算得到斯格明子不同時刻的擴散速度大小，斯格明子的擴散速度在x方向和y方向都以0為中心隨機分布，如圖8(b)和(c)所示. 通過對擴散速度大小進行統計，發現斯格明子的擴散速度分布服從高斯分布，如圖8(d)和(e)所示，這與經典的布朗運動特征一致.

圖7 樣品顯微圖

(a)運動軌跡圖

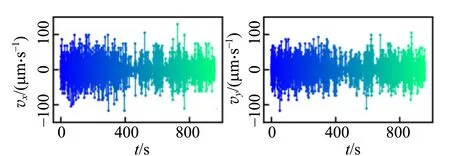
(b)x方向擴散速度 (c)y方向擴散速度

(d)x方向速度分布 (e)y方向速度分布圖8 溫度為320.6K時磁性斯格明子隨機熱運動行為的實驗測量結果

3.2 斯格明子熱運動行為隨溫度的變化

使用與磁光克爾效應顯微鏡配套的變溫樣品托，研究了溫度對斯格明子熱運動行為的影響，如圖9(a)～(c)所示. 當溫度升高時，斯格明子的熱運動現象會變得更加劇烈. 通過計算均方位移，可以對不同溫度下的擴散行為進行定量描述，如圖9(d)所示. 在不同溫度下，均方位移與統計間隔時間均表現出良好的線性關系. 通過線性擬合，可以得到不同溫度下斯格明子運動的擴散系數，如圖9(e)所示. 可以看出，隨著溫度的增加，擴散系數呈現出非線性的上升行為，這與愛因斯坦的線性溫度相關擴散理論存在差異. 我們認為這一非線性行為來源于樣品中隨機分布的缺陷對斯格明子運動的釘扎作用，而使用將愛因斯坦的線性溫度擴散關系與描述從缺陷中熱激發的Arrhenius形式函數相乘所得到的表達式

可對這一非線性行為進行較好的擬合，如圖9(e)中的綠色曲線所示. 從擬合參量還可以得知樣品中缺陷的平均釘扎勢Ep約為8.2 meV，而斯格明子熱運動的激活溫度T0約為305.3 K，即只有當環境溫度高于溫度T0，斯格明子才有較大機會從缺陷中逃逸，進而表現出隨機熱運動的行為.

(a)T=306.3 K (b)T=314.9 K (c)T=326.5 K

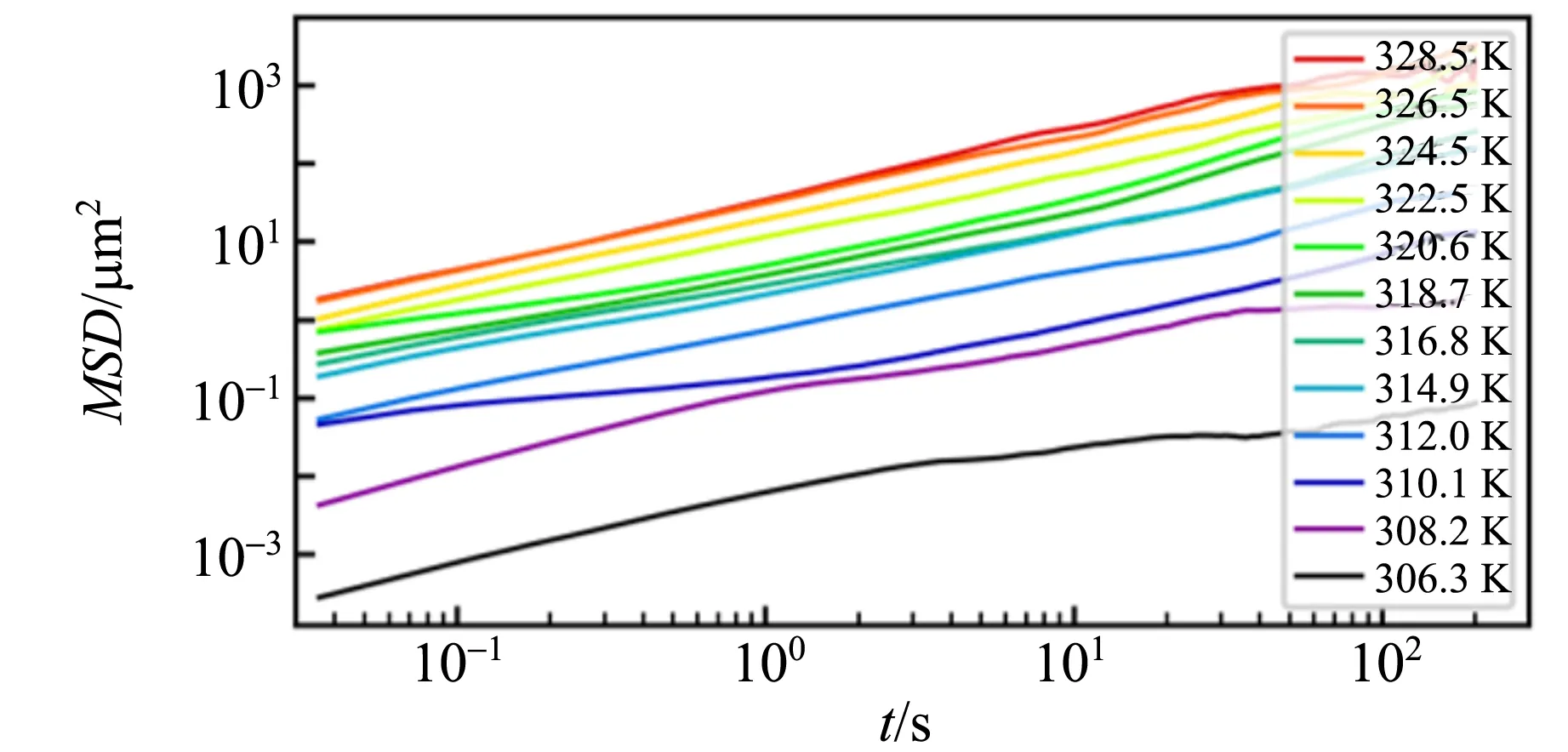
(d)不同溫度的擴散行為

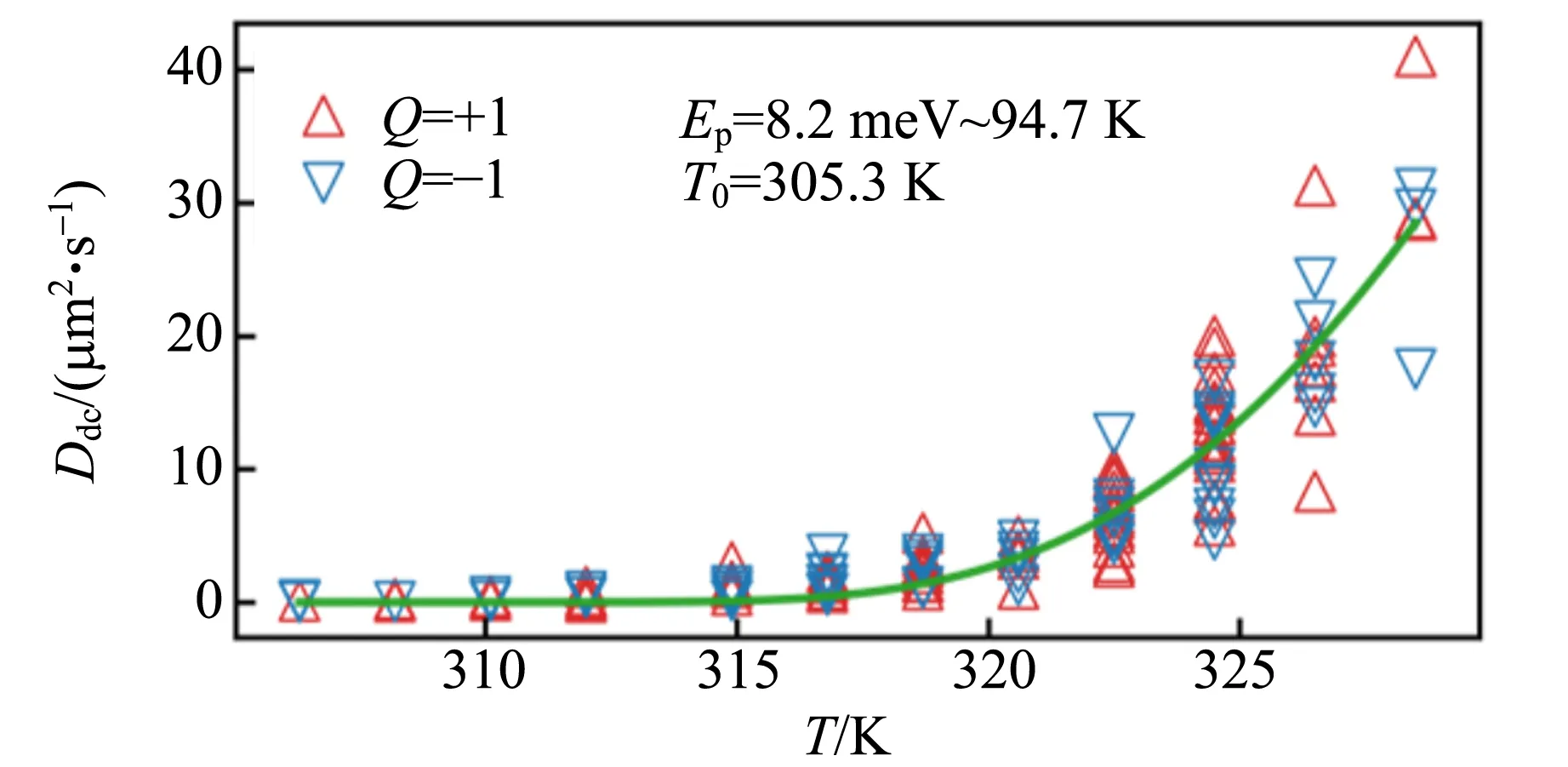
(e)不同溫度下斯格明子運動的擴散參量

圖9 斯格明子的熱運動行為隨溫度的變化關系

3.3 斯格明子旋性布朗運動的實驗驗證

為了研究斯格明子拓撲相關的旋性熱動力學行為，定義了斯格明子旋轉角θsr，它描述的是斯格明子運動過程中相鄰時間間隔速度矢量的夾角，如圖10所示. 根據隨機Thiele方程

可以計算得到斯格明子旋轉角的表達式為

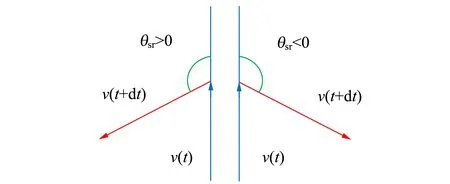
圖10 斯格明子旋轉角示意圖

由此可以看出，斯格明子旋轉角θsr是與拓撲電荷數Q直接相關的. 基于隨機LLG方程的微磁學模擬表明，Q=+1和Q=-1的斯格明子在做布朗運動的同時會分別向順時針和逆時針方向旋進，如圖11(a)和(b)所示. 通過計算斯格明子旋轉角θsr，可以非常明顯地看到Q=+1的斯格明子具有小于0的斯格明子旋轉角，而Q=-1的斯格明子具有大于0的斯格明子旋轉角，如圖11(c)所示. 通過分析實驗中采集到的斯格明子位置信息與速度信息，也可以得到相同的現象. 如圖11(d)和(f)所示，Q=+1的斯格明子旋轉角為負，對應于順時針旋進行為；而Q=-1的斯格明子旋轉角為正，對應于逆時針旋進行為. 這證明在實驗中確實觀測到了單個磁性斯格明子的旋性布朗運動現象.

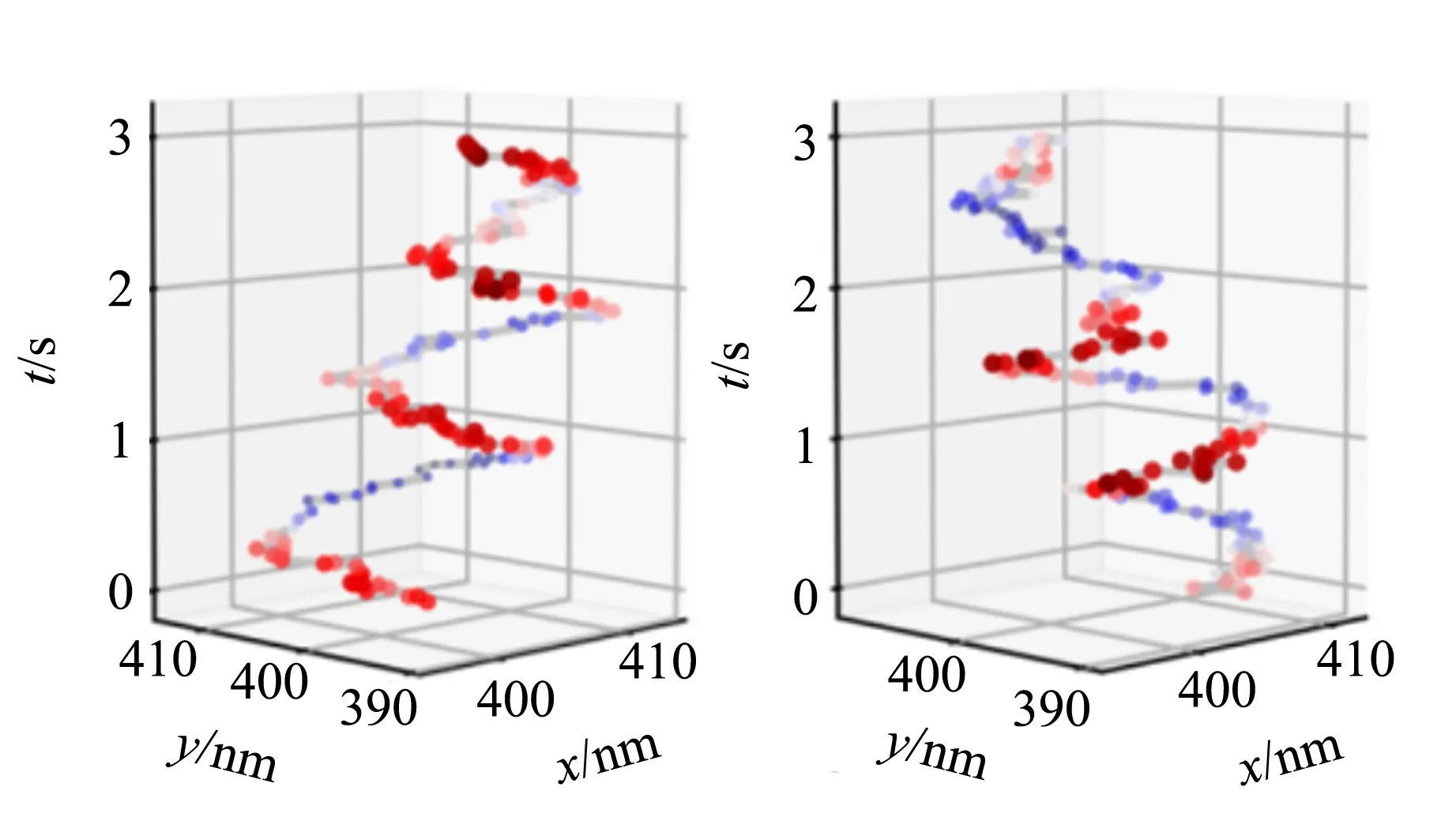
(a)Q=+1(模擬) (b)Q=-1(模擬)

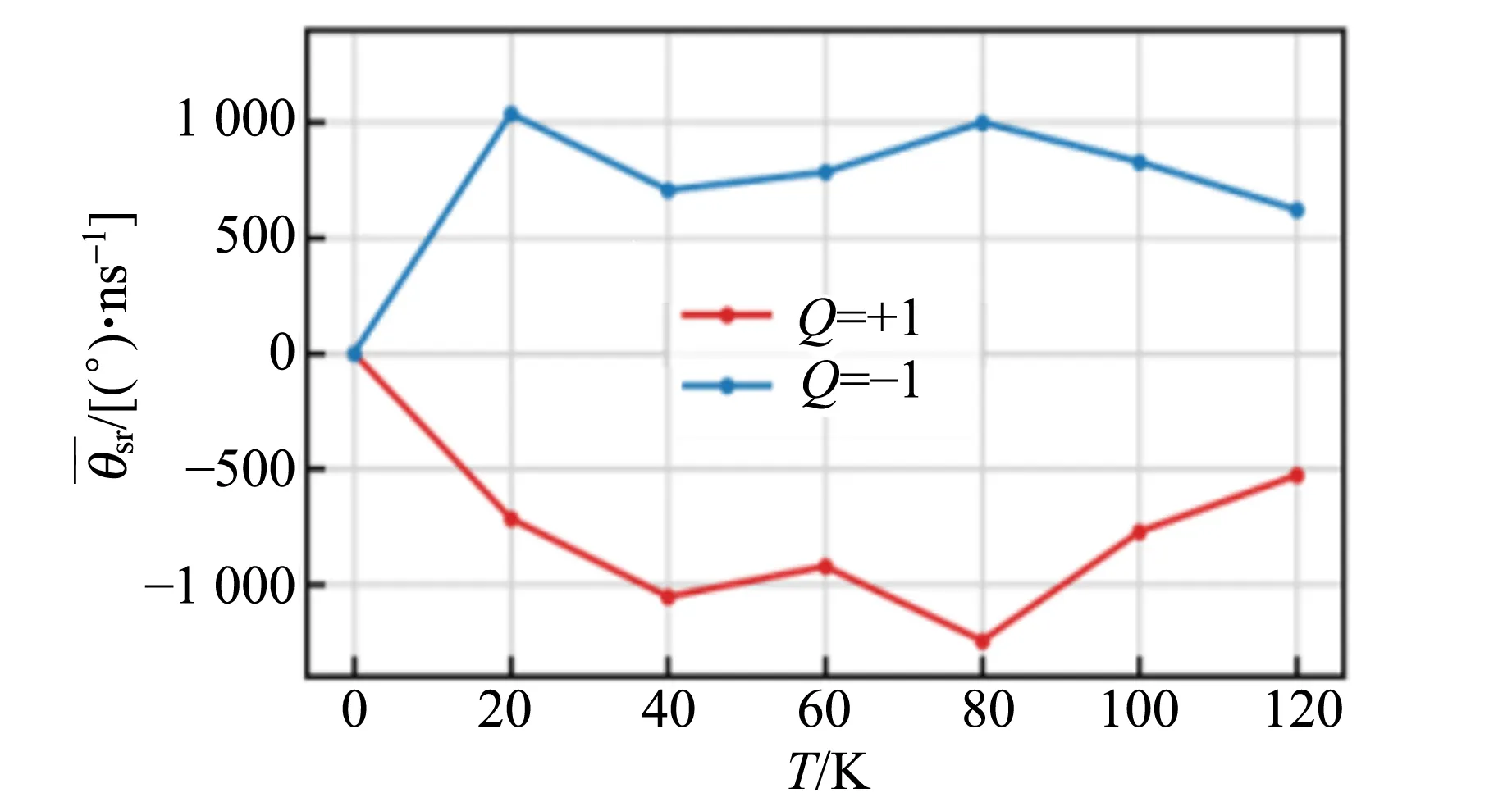
(c)θsr與T的關系(模擬)

(d)Q=+1(實測) (e)Q=-1(實測)

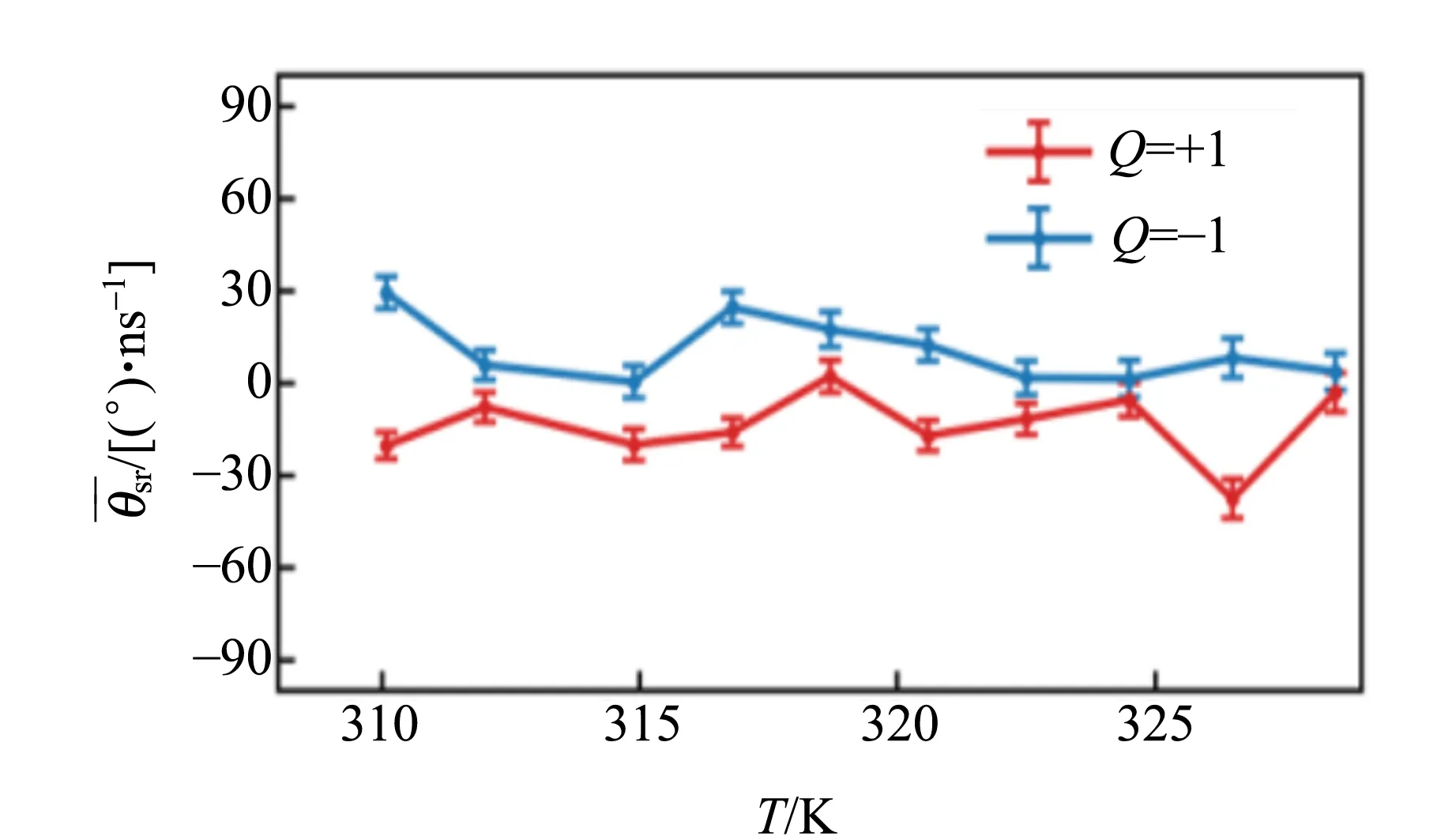
(f)θsr與T的關系(實測)圖11 斯格明子旋性布朗運動的數值模擬與實驗觀測結果

4 結束語

簡述了布朗運動和磁性斯格明子的基本知識以及磁性斯格明子的相關實驗研究進展，進一步介紹了單個斯格明子的布朗運動現象，包括其隨溫度非線性增加的擴散系數以及與拓撲相關的旋性運動行為. 磁性斯格明子是一種潛在的信息存儲單元，在未來自旋電子學器件中可能會發揮重要的作用，斯格明子拓撲相關熱運動行為也為器件設計與應用提供了更多可能性.