帶有狀態時滯的非線性隨機系統高斯濾波方法
王 碩, 何定洲, 朱 勇, 沈敦亮, 于 霖
(中國運載火箭技術研究院 北京宇航系統工程研究所,北京100076)
0 引 言
時滯問題的存在會對系統運行造成不良的影響,如造成系統振動、性能退化和甚至失穩等現象。近年來,在信號處理、通信和控制等領域采用非線性離散隨機系統,而對其非線性狀態的獲得大多利用觀測數據來近似估計[1-4]。通常,對非線性離散隨機系統的狀態估計問題的研究主要集中在一階隨機模型或一階馬爾可夫模型。但在實際應用中,很多機械和電氣動態系統則是二階模型或高階非線性連續時間隨機模型,不是一階模型[5-6]。這種高階連續時間模型進行離散化時,必然會出現時滯的狀態。因此,需要研究一種能夠對帶有狀態時滯的非線性離散隨機系統進行近似估計的方法。
對于帶有狀態時滯的非線性狀態估計問題通常采用H∞濾波[7-8]和粒子濾波[9-10]等方法進行解決,針對此問題學者們開展了大量的研究。Shi和Shan等對帶有時變狀態時滯和隨機狀態時滯控制系統的穩定性進行了研究[11-12]。Gu等針對帶有多狀態時滯的狀態空間問題,提出了最小二乘辨識算法[13]。Fang等對離散線性系統同步輸入和狀態估計的穩定性進行了研究[14]。Shi等針對帶有兩步隨機時滯的網絡控制系統提出了魯棒混合H2/H∞控制器[15]。文獻[16]給出了帶有d步狀態時滯的多變量狀態估計方法,在此基礎上,文獻[17]提出了聯合估計系統參數和狀態遞歸最小二乘方法。雖然這些方法不需要對概率密度函數(Probability density function,PDF)進行任何假設,但為了得到更高的估計精度,采用粒子濾波算法不可避免地會因為大量的隨機樣本而產生巨大的計算量,或采用H∞濾波需要復雜的計算矩陣不等式。特別對于帶有狀態時滯的情況,這些復雜的計算量會進一步增加。主要是因為當把狀態時滯認定為非線性離散隨機系統的一部分時,除了要對當前狀態進行近似估計外,所有的狀態時滯也要進行近似估計,這必然會產生更大的計算量。因此,需要研究一種狀態時滯的高斯濾波算法。
對于一般的非線性離散系統,常用的高斯濾波(GF)框架沒有考慮帶有狀態時滯的情況[18]。在GF框架下,通過不同的數值計算形式來近似非線性積分已經取得大量的研究成果。其中,最為突出且被廣泛應用的是擴展卡爾曼濾波器(EKF)[19-20],它是通過對非線性方程的一階線性化得到的。但是一階線性化得到的近似精度不高,經常會出現重大的偏差,甚至產生發散的情況。此外,其對雅可比矩陣的推導也是不容易的,尤其面對高維和不連續非線性系統的情況。
在文獻[18]的GF框架下,基于確定性采樣的數值技術來近似非線性積分,已取得了大量的研究成果,包括基于無跡變換的無跡卡爾曼濾波器(UKF)[22-23]、基于正交規則的高斯埃爾米特濾波器(GHF)、基于斯特林多項式插值的差分濾波器(DDF)和中心差分濾波器(CDF)等[24-26]。這種基于GF的確定性采樣不需要計算雅可比矩陣,且計算復雜度與EKF類似[21]。但他們至少可以達到二階的近似精度,高于EKF的一階近似精度。熊和吳等提出了一套關于精度、效率和穩定性的性能指標來分析和比較這些濾波器,促進在實際應用中對不同濾波器的選擇,且給出了上述濾波器穩定的充分條件[27-28]。
Arasaratnam等針對UKF、EKF、DDF和GHF不適合處理高維非線性系統的問題,基于球徑容積法則進一步提出了容積卡爾曼濾波器(CKF)[29]。Jia等提出一種新的非線性稀疏網格正交濾波器(SGQKF),精度比UKF、CDF、DDF和CKF更高,計算效率也比GHF更好[30]。陳紅梅等將SGQKF應用在觀測信息不完全且隨機干擾不確定的非線性系統,并給出算法穩定性的證明[31]。Wang等針對過程噪聲和量測噪聲相關的非線性系統設計了一種高斯近似遞歸的濾波器[32]。
上述GF算法均是建立在同一假設條件下,即不考慮系統帶有狀態時滯的情況。但在實際工程的應用中,時滯問題一直存在。目前,針對帶有狀態時滯非線性隨機系統最優估計問題的解決尚不夠完善,尤其對系統狀態時滯和量測時滯同時存在的情況研究甚少。受文獻[18]啟發,本文針對帶有狀態時滯系統的最優估計問題,提出了一種新的高斯濾波框架,給出了其在三階球徑容積法則下的具體實現形式—狀態時滯容積卡爾曼濾波器(SDCKF),可以很好地解決系統帶有狀態時滯的非線性估計問題,易于工程實現。
1 問題描述
考慮具有多個狀態時滯的非線性離散隨機系統,具體形式為:
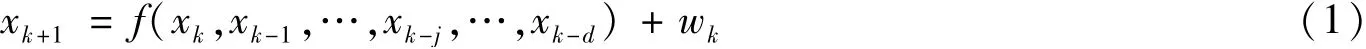


2 帶有狀態時滯的GF算法
由上述描述可知,標準GF算法未考慮系統帶有狀態時滯的情況。對標準GF算法進行改進,如式(1)

2.1 時間預測

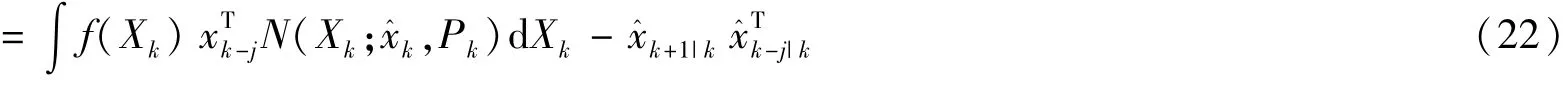
2.2 量測更新

2.3 帶有狀態時滯的GF算法實現
由定理1和定理2不難發現,對于多維高斯加權積分的計算問題,是實現本文所提出改進GF算法的主要難點。針對此問題,本文擬采用數值積分來近似非線性函數的方法實現。三階球徑容積法則是近些年提出的,且是較優越的線性化方法,該方法具有良好的數值穩定性和近似精度。因此,本文給出基于三階球徑容積法則的改進GF算法—SDCKF濾波算法。三階球徑容積法則如下:
2.3.1 三階球徑容積法則
針對式(14)~式(16)、式(26)和式(28)的非線性高斯加權積分,可以統一為如下形式:


3 仿真分析
通過非線性模型式(50)和式(51)來驗證本文所提出SDCKF算法的有效性,并從非線性狀態估計精度

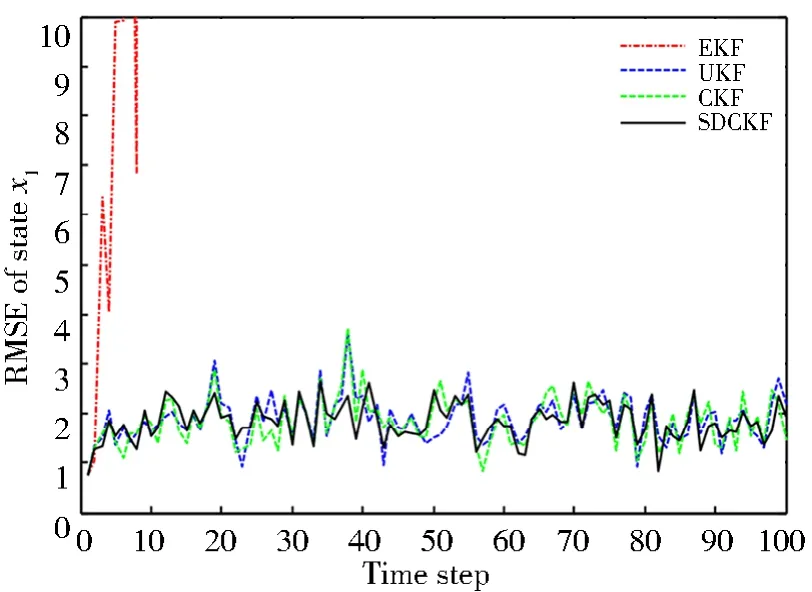
圖1 狀態x1的RMSEFig.1 RMSE of state x1
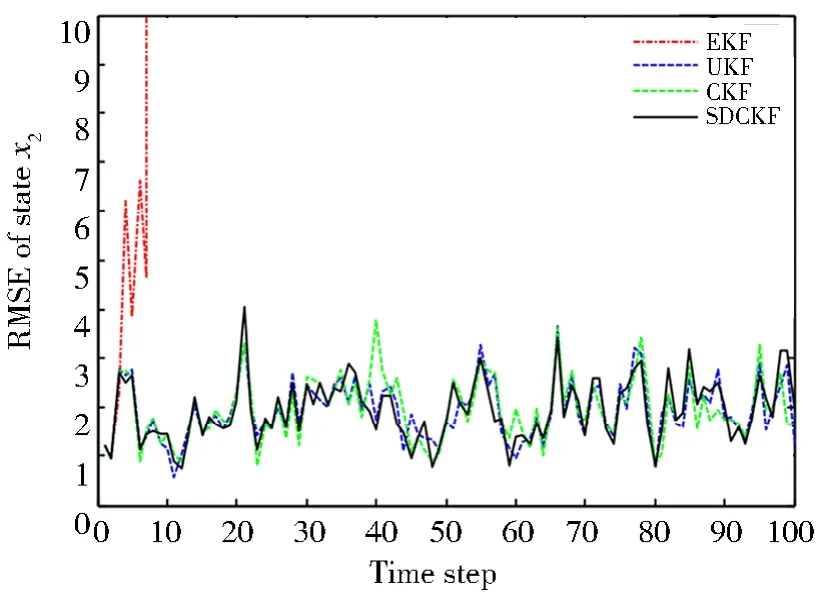
圖2 狀態x2的RMSEFig.2 RMSE of state x2
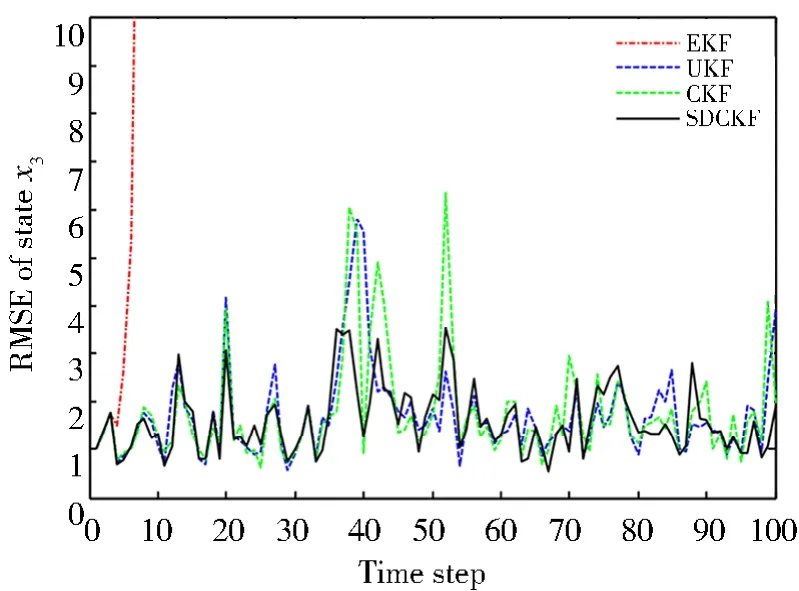
圖3 狀態x3的RMSEFig.3 RMSE of state x3
從仿真結果可以看出,EKF算法很快便出現了發散現象,表明EKF算法面對模型式(50)這種帶有狀態時滯的強非線性狀態估計問題,很難進行狀態估計。出現這種現象的原因可能是EKF算法在進行后驗狀態估計時對非線性方程的線性化誤差變大,導致逼近非線性函數的雅可比矩陣發散,進而使得系統失穩。UKF算法和CKF算法也都獲得了比較好的狀態估計結果,數值穩定性較高。但是,由于系統狀態時滯的存在,使得UKF算法和CKF算法的狀態估計精度有所下降,在圖3中表現比較明顯,在仿真第40步和50步時誤差突然變大,這可能是狀態x3綜合了狀態x1和狀態x2的誤差所導致,這種狀態估計誤差突然變大的現象,在實際工程應用中可能會帶來非常嚴重的后果。可以看出,本文所提出的SDCKF算法與UKF算法、CKF算法幾乎具有相同的狀態估計精度,或略高于這兩種算法。但是,SDCKF算法的數值穩定性明顯高于UKF算法和CKF算法,SDCKF算法未出現誤差跳變、突然增大等情況。綜合上述分析結果,本文所提出的SDCKF算法可以很好地解決帶有狀態時滯的非線性隨機系統的狀態估計問題。
4 結 論
針對傳統高斯濾波算法不能很好地解決系統帶有狀態時滯的非線性狀態估計問題,給出了一種改進的高斯濾波算法-狀態時滯容積卡爾曼濾波器(SDCKF)。給出了在三階球徑容積法則下的具體實現形式,可以有效地避免因為狀態維數過高而引起濾波算法穩定性下降的問題。通過帶有狀態時滯的非線性函數示例,將SDCKF算法與經典非線性濾波方法EKF算法、UKF算法及CKF算法進行仿真對比分析。仿真結果表明,SDCKF算法具有更好的數值穩定性和狀態估計精度,證明了SDCKF算法可以很好地解決系統帶有狀態時滯的非線性狀態估計問題。

