非視距環境下基于二階錐規劃的RSS定位算法

金小萍，梁俊，謝少楓

（中國計量大學，浙江 杭州 310018）

1 引言

近年來，無線傳感器網絡（wireless sensor network，WSN）由于其低能耗和高效率，而在目標跟蹤、室內定位、海上救援、森林火災監測等領域得到了廣泛的研究與應用。在WSN應用中，獲取傳感器節點的位置是必不可少的部分，關于節點位置確定的定位技術主要有如下兩大類。

· 第一類：基于非測距的方法，如重心法、DV-HOP、APIT等方法[1-2]，這些方法雖然易于實施，成本較低，但定位精度受傳感器網絡布置的限制。

· 第二類：基于測距的定位方法，如RSS、AOA、TOA、TDOA等方法[3-5]，相比非測距方法，這些方法雖然需要額外的測距硬件，但定位精度更高，其中基于RSS的測距方法僅需要測出信號的衰減信息，且硬件實現成本相比其他測距方式也更低，在小規模傳感器網絡中，是一種高性價比的定位方式。然而基于RSS測距方式的定位精度易受非視距（non-line-of-sight，NLOS）環境的干擾，尤其是在障礙物密集的室內環境中，例如地下車庫、監獄、醫院等室內場景。在對人員進行定位時，墻壁、人流、房間的非視距干擾就很大，如果仍將傳感器之間假設為視距（line-of-sight，LOS），則會導致RSS信息收集的不準確甚至RSS信息的丟失，最終造成較大的定位誤差。

以往關于非視距環境下RSS定位問題的研究，主要包括3種類型。第一種方法基于非線性優化算法，參考文獻[6]利用高斯混合模型將噪聲項的非視距與視距分布變換為指數形式后再利用牛頓法進行求解。參考文獻[7]基于最大似然（maximum likelihood，ML）準則構建了一個非線性方程組，合理設置初始點，再利用牛頓迭代法的思想進行求解。然而，此類方法需要對噪聲誤差以及非視距環境具有良好的認知，且非線性優化算法本身就存在估計誤差較大的問題，定位精度無法保證。第二種方法基于加權最小二乘（weighted least squares，WLS）算法，此類方法的思想是將問題轉化為線性的估計器再利用二分法進行求解。參考文獻[8]使用無味變換（unscented transform，UT）將基于RSS的傳感器定位問題轉換為WLS估計問題應用于室內定位模型中，但該方法仍然需要對非視距狀態具有良好的認知。參考文獻[9]應用平方域（squared range，SR）和最小二乘（least squares，LS）準則將非視距偏差作為平衡干擾參數與目標位置一起進行估計，最終構建了一個WLS問題，但其中線性化的近似會帶來額外的誤差，從而導致求解精度不夠準確。第三種方法基于凸優化技術，此類方法的思想是將非凸的定位問題轉化為凸問題求解，參考文獻[10]研究了RSS與TOA在非視距環境中的定位算法，對誤差項進行一階泰勒公式展開，在此基礎上利用LS準則構建了定位問題，最終將原始的非凸問題轉換為二階錐規劃（second-order cone programming，SOCP）問題，雖然此類方法可以有效地提高定位性能，但由于TOA定位對硬件要求較高，再結合RSS和TOA信息硬件設備的實現難度較大，并且將測距方程進行泰勒近似，會造成一定的誤差。

基于上述背景，提出了一種基于SOCP的魯棒性定位算法，與參考文獻[6-10]不同，本文考慮在非視距干擾量的影響達到最大的情況下去處理非視距RSS定位問題。首先，利用對數乘法法則將RSS模型化為線性乘積形式，接著，采用最小平方相對誤差（least squares relative error，LSRE）準則[12]構建了魯棒性的節點定位方程，然后，利用凸優化技術提出了SOCP算法，從而解決原始定位問題的非凸性，最后，將問題推廣到未知發射功率的情況，提出了迭代估計的SOCP算法。與以往的方法相比，所提算法不用識別非視距的狀態以及分布，僅考慮非視距偏差達到最大的最壞情況，對非視距偏差具有魯棒性，減輕了非視距偏差的影響，從而提升了定位性能。

2 非視距RSS系統模型及問題分析

考慮一個二維平面的無線傳感器網絡，該傳感器網絡具有N個錨節點si(i=1,…,n)，錨節點固定位置用來接收未知的待定位目標節點x的RSS信息，如圖1所示，假定目標節點向錨節點發出信號，錨節點可以良好地從接收信號中提取RSS信息，在非視距環境下，對應著第i個錨節點的接收信號強度為[10-11]：其中，P0是參考距離處的發射功率（dBm），γ是路徑損耗指數，d0是參考距離，設置為1 m，ni是測量的噪聲誤差量，一般設定服從零均值的高斯分布， 如ni～N(0,Oi2)。bi是非視距偏差（當bi=0的時候，i∈lLOS，當bi＞0，i∈lNLOS，其中lLOS與lNLOS分別代表視距傳感器和非視距環境下的傳感器的數目，對應的有lNLOS=N-lLOS），在本文中，假設非視距偏差的大小受一個已知常數bmax的限制， 如0 ≤bi≤bmax，·均表示二范數運算。

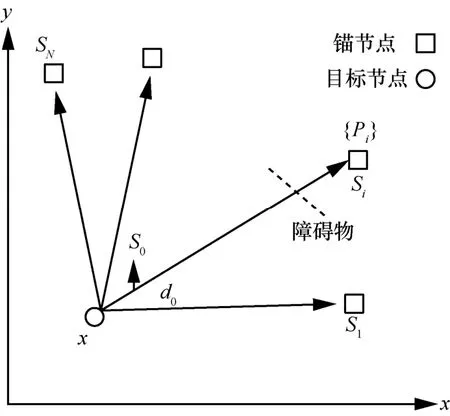
圖1 RSS定位示意圖

基于式（1）中的測量值Pi，可以得到關于未知節點x和bi(i=1,…,n)的最大似然估計：

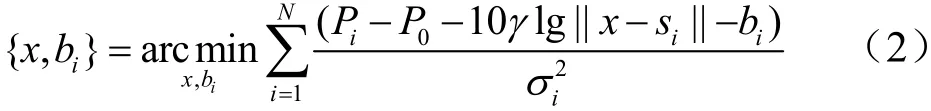
式（2）的求解非常困難，由于未知的非視距偏差ib的存在，該問題的解是不確定的，需要去識別傳感器節點之間的連接狀態，才可以求解；其次，式（2）中的目標函數具有嚴重的非凸和非線性，難以獲取全局最優解。為了解決這些問題，在第3節中，將通過假定非視距偏差的上界來構建魯棒優化問題，以此克服非視距偏差的影響，并利用凸優化技術處理定位估計中求解量是非全局最優的問題。

3 魯棒性SOCP定位算法

3.1 已知發射功率

首先，在發射功率已知（即0P已知）的情況下推導魯棒性SOCP定位算法。針對式（1），在其兩邊同時加上變形移項后得到：

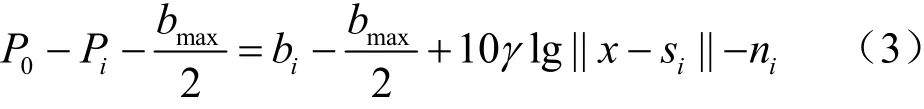
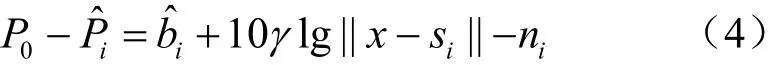
利用對數運算法則，將式（4）改寫為線性乘積形式：

基于式（5）的乘積形式，得到如下關于未知節點x的魯棒最小平方相對誤差（robust least squares relative error，R-LSRE）估計表達式[12]：

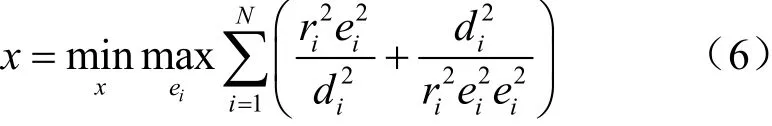
該問題就是在最壞的情況下，對節點估計方程進行魯棒優化，也就是最大化ie的情況下再最小化該目標函數。與參考文獻[10]中利用LS估計構建的目標函數相比，LSRE估計比LS估計具有更好的估計精度[12]。此外，由于考慮了非視距干擾量的影響達到最大的最壞情況，對非視距偏差量具有魯棒性，故利用該估計方法可以減輕非視距偏差帶來的影響。

為了解決式（6），以ie為自變量，引入一個函數y=f(ei)，可以得到：

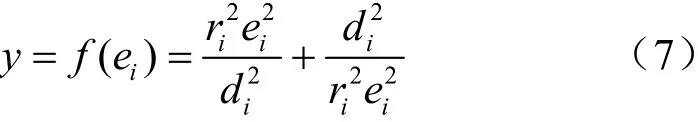
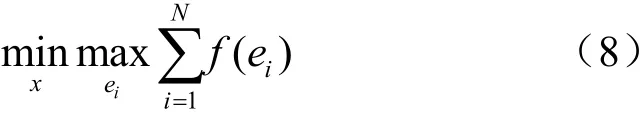
要解決式（8）對應的問題，需要計算函數算該問題，分為兩種情況進行分析：

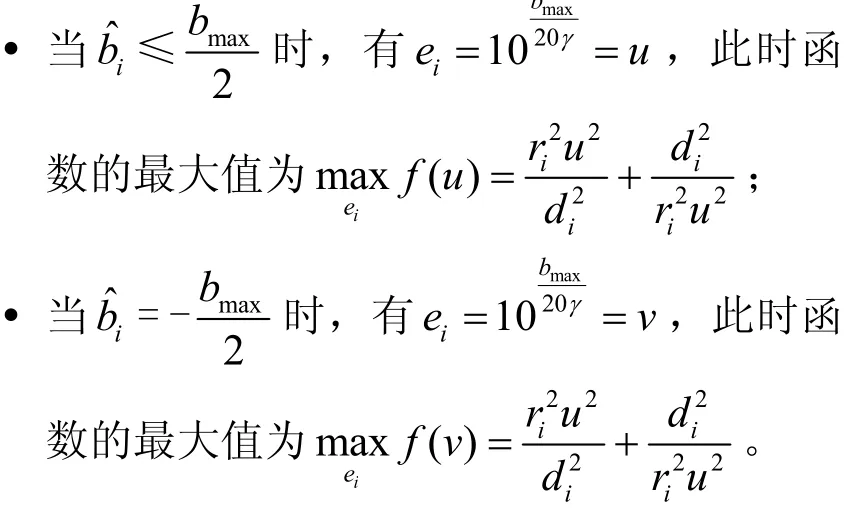
基于上述兩種情況，式（8）可以等價為如下最優化目標節點問題：

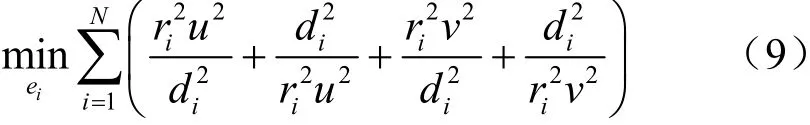
式（9）中最優化問題的目標函數是非凸非線性的。針對該問題，將利用凸優化松弛技術將原始節點估計問題轉化為一個SOCP問題，首先，式（9）可以等價為如下上鏡圖形式問題[13]：

其中，t1i、t2i、t3i、t4i分別是所對應的約束條件的第i個變量的上界。

可以看出目標函數是線性的，而約束條件仍為非凸的。引入二個等價變量和基于此，把約束條件（10b）和引入的二個等價變量同時松弛到二階錐（second-order cone，SOC）中，最終式（10）轉變為[13]：

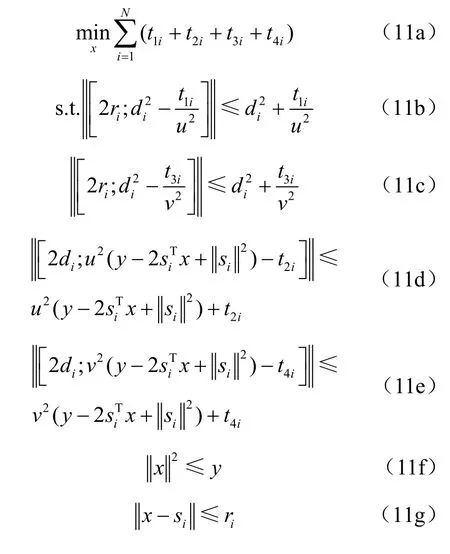
這是一個標準的SOCP問題，可以由內點法求解未知的目標節點，具體可由CVX仿真軟件實現[14]，在后續描述中，將該發射功率已知的魯棒性SOCP定位算法定義為R-SOCP。

3.2 未知發射功率

在實際情況下，傳感器的發射功率0P往往隨著外部環境的變化而發生改變，而這將造成額外的定位誤差，針對這一情況，本節將在定位方法（11）的基礎上進行改進，并通過一個迭代SOCP算法來提升性能。

當發射功率未知時, 等價于di參數未知。重新改寫式（5），可以得到：

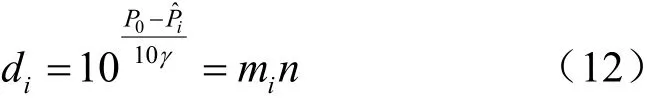
其中，對應參數n是未知量，類似地，可以得到如下最優化問題：

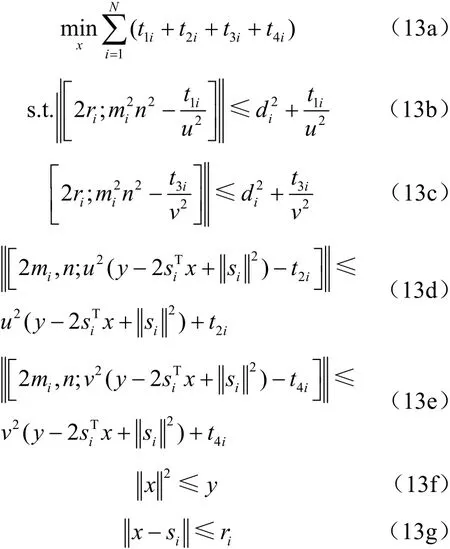
對于問題（13），其中的約束條件（13b）和（13c）是非凸的，因為其中的未知量在二階錐約束中是非仿射非線性的。通過添加二階錐松弛條件將發射功率量等價成偽線性形式，由此，式（13）可以二階錐松弛（second-order cone relaxation，SOCR）為[13]：

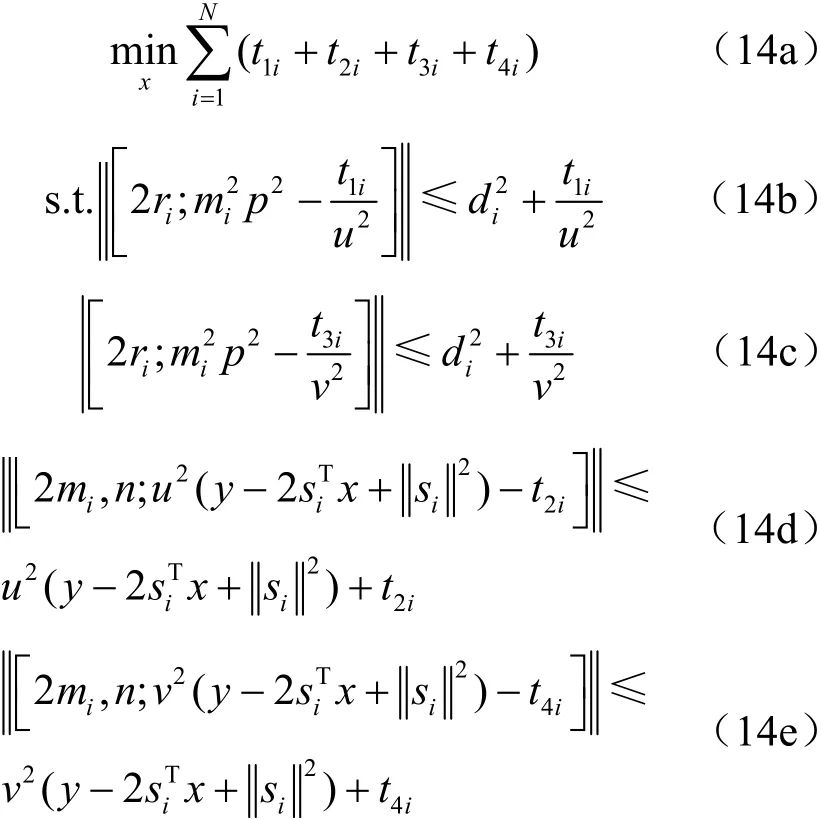
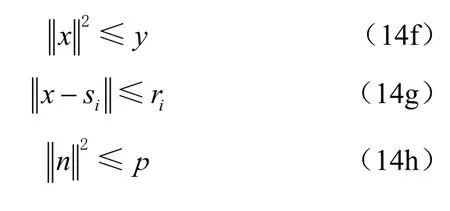
式（14）也是一個SOCP問題，同樣可由內點法求解，此外，為了進一步提升式（14）中SOCP方法的性能，提出了一個同時估計發射功率與目標位置的迭代SOCP算法，如算法1所示，后續把發射功率未知時的魯棒性SOCP定位算法定義為R-SOCP-U，最終，將所推導的發射功率已知與發射功率未知情況下的魯棒性SOCP定位算法歸納如下。

算法1魯棒性SOCP定位算法

步驟1輸入錨節點位置{si}；最大非視距偏差為{bmax}；噪聲標準差為{σi}；路徑損耗指數為{γ}；接收信號強度為{Pi}；發射功率為{P0}；最大迭代次數為{kmax}；極小正值為{}δ；

步驟2當發射功率已知，求解式（11），得到估計的目標位置；當發射功率未知，求解式（14），得到估計位置xk1-，令k=1；

步驟3將xk1-代入式（1）中，反解出發射功率pk-1：

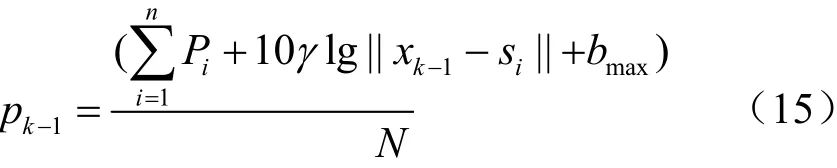
步驟4利用Pk-1求解式（11），得到估計位置xk；

步驟5判斷如果＜δ或者k＞kmax則得到估計的目標位置，如果不是，則令k=k+1，重新計算步驟3。

輸出步驟2或步驟5的目標節點的位置x。

4 定位性能仿真

在定位性能仿真中，主要選擇了3種方法用來對比R-SOCP與R-SOCP-U算法：基于牛頓迭代思路的NR法[7]、基于WLS的UT法[8]、基于LS的SOCP法[10]。其中，SOCP等凸問題可使用CVX軟件包進行仿真，并且仿真中只涉及RSS算法的部分。定位環境設定如下：所有傳感器均勻設定在30 m×30 m的平面區域，其中的仿真參數設定如下：發射功率P0=-4 0 dBm ，路徑損耗指數γ=4。簡單起見，假設RSS測量模型的所有噪聲標準差都相等，也就是σi=σ。定位的性能采用均方根誤差（root mean square error, RMSE）進行分析，定義如下：

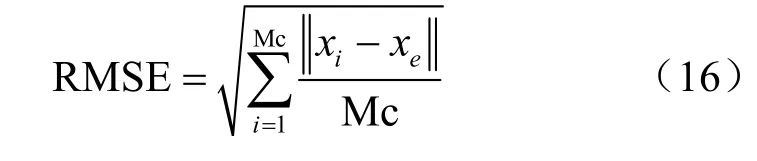
其中，Mc是蒙特卡羅仿真次數，本次仿真，進行運算3 000次，ix為第i次不同定位算法運算所產生的估計位置，ex為每次實驗當中隨機產生的目標節點的真實位置。

圖2展示了R-SOCP算法的RMSE與噪聲標準差σ之間的關系的性能比較圖形，設定噪聲標準差從1 dB到6 dB均勻地增加。如圖2中顯示，所有算法的RMSE都隨著σ的增長而變大，這是因為隨著環境中的噪聲干擾增加，傳感器接收的信號會受到較大的干擾，從而造成誤差。最后，圖2顯示，對于所有考慮到的σ跨度，所提出的R-SOCP算法的定位誤差是最小的，優于現有的算法。

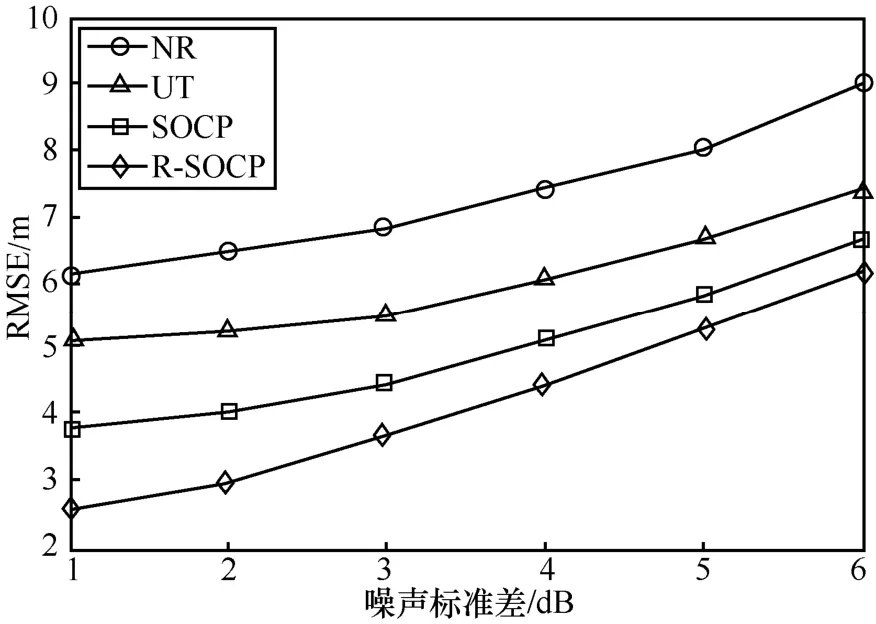
圖2 RMSE隨著噪聲標準差變化

圖3展示了R-SOCP算法的RMSE與錨節點數目N之間的關系的性能比較圖形，設定σ= 3 dB，lNLOS=N，bmax= 6 dB ，錨節點數目從4到10均勻增加。可以看出，隨著N的增加，所有算法的RMSE都會變得更小。這是因為隨著錨節點數量的增加，目標節點可以從錨節點處獲取更多的信號信息，從而提高定位精度。此外，當布置的錨節點傳感器多于8個的時候，所有算法的RMSE將趨于平穩，這是因為當N很大時，在網絡中收集的RSS信息足以使所有算法的性能達到最好。最后，圖3顯示，與其他算法相比，隨著N的增加，所提出的算法的RMSE也是最低的，例如，當N=10時，R-SOCP算法的RMSE=3.4 m，相比SOCP、UT和NR算法的性能分別提高了0.7 m、2.1 m、3.3 m。

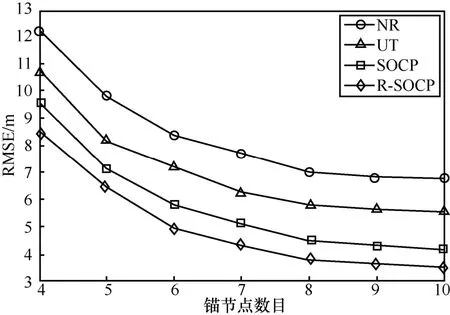
圖3 RMSE隨著錨節點數目變化

圖4展示了R-SOCP算法的RMSE與非視距錨節點數目lNLOS之間的關系的性能比較曲線，設定σ=3 dB，N=8，bmax= 6 dB ，錨節點中非視距傳感器的數目lNLOS從2個一直增加到8個。可以看到，R-SOCP算法的RMSE始終要低于SOCP、UT和NR算法，其定位誤差是最小的。此外，基于牛頓迭代思路的NR法和線性近似的UT法會隨著非視距傳感器數目的增多而降低定位性能，因為其不能良好地識別非視距傳感器。而所提出的R-SOCP和SOCP算法都顯示了對非視距偏差的良好緩解能力，其定位性能不會隨著傳感器網絡中的非視距錨節點數目而改變，其中R-SOCP算法由于考慮了非視距偏差達到最大的最壞情況下非視距傳感器的誤差干擾，不用再去識別非視距傳感器，對非視距偏差具有魯棒性，從而減輕了非視距偏差的影響，帶來了性能上的提升。

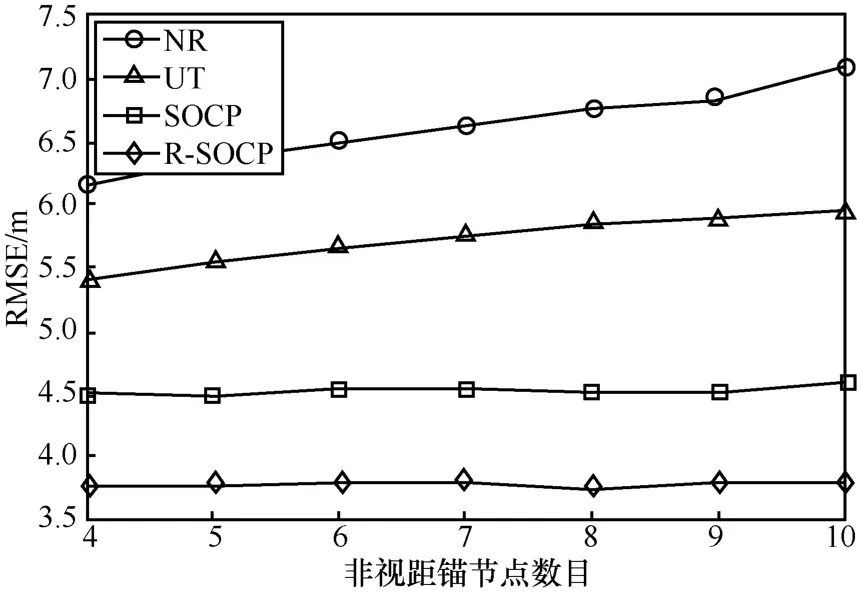
圖4 RMSE隨著非視距錨節點數目變化

圖5展示了R-SOCP算法的RMSE與最大非視偏差bmax之間關系的性能比較曲線，設定σ= 1dB ，N=lNLOS=10，最大非視距偏差bmax從1 dB到6 dB均勻增加。可以看出，所有考慮的算法的RMSE都會隨著bmax的增長而變大。這是因為非視距環境越惡劣，RSS信號的接收也會受到很大干擾，從而造成誤差。此外，對于所有考慮的最大非視距偏差，本文所提算法都要優于其余的算法，最后，R-SOCP相比其他算法，性能分別提升了1 m、2.5 m、3.6 m。

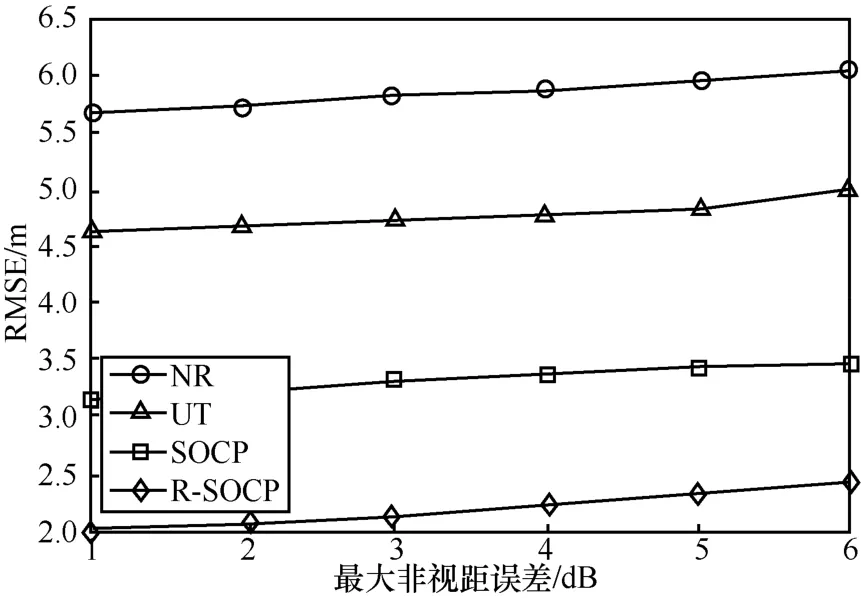
圖5 RMSE隨著最大非視距偏差變化

圖6展示了未知發射功率下的R-SOCP-U算法的累積分布函數（cumulative distribution function，CDF）性能對比曲線，設定bmax=6 dB，可以看出在未知發射功率下的R-SOCP-U算法的性能相比于SOCP算法以及UT算法都要好，具體而言，當估計誤差為2 m時，R-SOCP-U算法的累積分布函數為95%，SOCP算法的累積分布函數為86%，UT算法的累積分布函數為58%，也就是說在3 000次蒙特卡羅仿真運算中、95%的情況下，R-SOCP-U算法的估計誤差維持在2 m之內，可以得知，R-SOCP-U算法的定位精度是良好的。

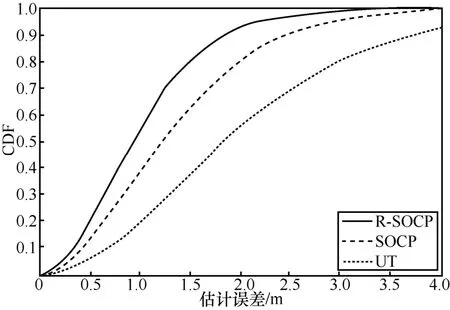
圖6 R-SOCP-U算法CDF曲線的性能對比

5 復雜度分析

對于所提出的魯棒性SOCP定位算法，其中SOCP問題是由內點法去求解[13]，其中內點法中每次的迭代復雜度為O(N3)，每次的迭代數目為ξ為設定的SOCP問題求解的精度，綜上可知，整體的運算復雜度為而求解NR法的牛頓迭代法解法的迭代次數設定為kmax，求解UT法的二分法解法設定最大迭代次數為kmax，它們的最差運算復雜度均為O(kmaxN)。可以看出所提魯棒性SOCP定位算法的運算復雜度與SOCP算法一致，但高于NR法與UT算法，權衡復雜度與定位精度，其性能是較好的。

6 結束語

針對非視距環境下的RSS定位，本文提出了魯棒性SOCP定位算法，該算法在假設非視距偏差上界的基礎上，無須獲取非視距偏差在實際環境中的統計信息和數目等情況，有效抑制了非視距偏差對定位性能造成的干擾。同時，將該算法推廣到未知發射功率的情況，提出了改進的迭代SOCP算法，通過將發射功率與目標位置同時迭代估計來提高定位性能。仿真結果表明，所提出的魯棒性SOCP定位算法對非視距偏差具有魯棒性，減輕了非視距偏差的影響，與現有的RSS非視距定位方法相比，也具有更好的定位精度。最后，本文所提出的基于SOCP的定位算法雖然定位精度較高，但存在運算復雜度較高的問題，在之后的研究中，將重點解決復雜度較高的問題。