基于改進BB-BC算法的輪轂電機直驅賽車行駛策略優化

黃天一，張幽彤，張甲典

(1.北京理工大學 清潔車輛北京市重點實驗室，北京 100081；2.振發新能集團有限公司，江蘇，無錫 214028)

21世紀以來，新能源汽車正成為汽車技術變革的重要方向，其中，純電動汽車以其零排放、低噪聲等優點而備受青睞。同時，隨著電動汽車技術的不斷推進，輪轂電機直驅技術開始得到廣泛的應用，尤其是各類電動車賽事。

對于輪轂電機直驅賽車，由于省去了電機至驅動輪之間的傳動系統，機械效率大大提升；且輪轂電機體積小，整車重量得以降低，有利于提高續駛里程。國內外學者在整車能量管理和行駛策略方向開展了一系列研究。文獻[1]研究了影響輪轂電機直驅賽車能耗大小的關鍵因素，認為定速巡航為最佳的節能駕駛策略。文獻[2]依靠所建立的太陽能數據庫來估算預期的太陽能功率，并結合實時SOC值制定了賽車能量流在線能量管理策略。文獻[3]著眼于對太陽輻射強度的預測，基于機器學習對氣象大數據進行分析，但對于大跨度地區的不確定天氣，該模型精度有待提高。文獻[4]提出了一種基于太陽能輻射強度和目標距離的賽車能量優化方案，但其依賴于大量的外部數據。文獻[5]和文獻[6]分別根據所建立的功率平衡方程以及電池SOC值來估算賽車的最佳巡航速度，這種方法比較簡便，但動態性差。

在眾多智能優化方法中，BB-BC算法相比于遺傳算法GA、粒子群優化算法PSO等其他算法，在收斂性上有明顯優勢，但同時也常因候選解缺乏多樣性而陷入局部最優解，導致優化失敗[7]。本文以2019世界太陽能車挑戰賽（World Solar Challenge，WSC）為背景，對采用光伏電池和普通動力電池為動力源的輪轂電機直驅賽車行駛策略進行了研究。建立了整車能耗優化模型，并進行了模型參數的試驗驗證；通過引入一維混沌邏輯映射，在傳統BB-BC優化算法的基礎上形成改進的BB-BC算法，從而對輪轂電機直驅賽車的行駛策略進行優化，以縮短完賽時間。

1 輪轂電機直驅賽車優化模型

1.1 整車參數與模型架構

本文研究對象為雙輪轂電機直驅賽車，動力系統主要由光伏電池陣列、最大功率跟隨器、動力電池組、輪轂電機及電機控制器組成，系統結構如圖1所示。在比賽巡航模式下，由光伏電池陣列和動力電池一同為驅動系統供電。整車參數見表1。

圖1 輪轂電機直驅賽車動力系統結構

表1 賽車參數

根據整車動力系統結構，利用Matlab/ Simulink搭建輪轂電機直驅賽車優化模型。該模型是優化算法的仿真基礎，主要包括整車模型、負載模型以及WSC賽事的條件參數。優化模型架構如圖2所示。

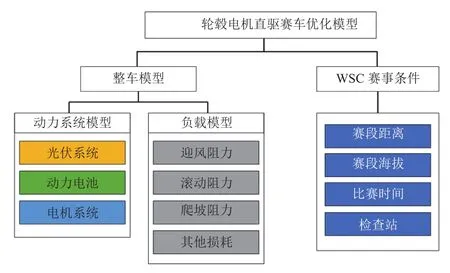
圖2 輪轂電機直驅賽車優化模型架構

1.2 光伏電池陣列模型

賽車的光伏電池陣列由串聯數為ns，并聯數為np的光伏電池組組成，其輸出特性可以表示為：

式中：Iph為光電流；Is為反向飽和電流；Isc為光伏電池短路電流；U為電池輸出電壓；q為電子電荷量，值為1.6×10-19C；n為二極管系數，值為28；K為玻爾茲曼常數，值為1.38×10-23；K1為短路電流溫度變化系數；T為電池表面溫度；T0為標準測試溫度，值為298 K；S為實際光強；S0為標準測試光強。

光伏電池特性參數見表2。

最大功率跟隨器（Maximum Power Point Tracking，MPPT）的作用是控制光伏電池兩端的輸出電壓，使其時刻工作在最大功率點上。本文將根據實測的MPPT工作特性，選取合適的MPPT效率值作為建模依據。

表2 SunPower光伏電池技術參數

1.3 動力電池模型

本文在Puekert電池放電公式的基礎上，利用電池放電功率代替電池放電電流，電池模型公式為：

式中：C為電池組額定容量；PB為電池組的放電功率；N為Puekert系數，可由試驗測得。

基于上式，短時間內T內的電池SOC計算公式為：

式中：SOCint為電池組初始SOC值。

1.4 電機及電機控制器模型

電驅動系統中，采用2個永磁同步輪轂電機，單個電機額定功率為3 kW，利用臺架試驗獲得的輪轂電機系統（電機+電機控制器）效率MAP圖作為模型輸入。單個輪轂電機系統效率MAP如圖3所示。

圖3 輪轂電機系統效率MAP

1.5 整車動力學模型

整車驅動力Fr的計算公式為：

式中：A為空氣密度；CD為風阻系數；V為車速；A為賽車截面積；Crr為滾阻系數，取值0.005 5；m為整車質量；g為重力加速度，取值9.8 m/s2；θ為道路坡度。

2 BB-BC算法

BB-BC算法，即大爆炸算法（Big Bang-Big Crunch Algorithm）[8]。該算法分為兩個階段——大爆炸（Big Bang）和大坍縮（Big Crunch）。BB過程代表著碎片解在整個搜索空間內隨機、無序地被拋出，BC過程則是碎片解因引力收縮至一個唯一的原子解。BB-BC算法在運行過程中將不斷地重復這一過程，直至到達算法的結束條件，終止運算。算法表述如下：

對n維連續變量，有目標函數f(x)，優化目的是使目標函數取得最小值minf(x)，候選解x用一個j維向量表示，其各維度分量其中xmin和xmax分別搜索空間的下界和上界。

2.1 “坍縮”過程

假設第1次迭代時產生了n個碎片解，對第1代碎片解進行“坍縮”，具體求解如下：

式中：xck為在坍縮過程中得到的j維原子解在k維度的坐標分量；xik為碎片解xi在k維度的坐標分量；f(xi)為碎片解xi的目標函數值。

2.2 “爆炸”過程

第2次迭代開始，將以上一代“坍縮”過程求得的原子解為中心進行“爆炸”，其求解方法如下：

式中：r為一個（-1，1）上的隨機數；a為收斂因子（0＜a＜1）；t為迭代次數。

為了保證“爆炸”過程中產生的碎片解不超過搜索空間范圍，分別設定上、下界xmax和xmin來校正結果。

3 改進的BB-BC算法

作為一種相對較新的群體智能優化算法，BB-BC算法不要求待優化函數連續可導，也不需要待優化函數的梯度信息。在實際運用中，該算法以收斂速度快而著稱。

但從BB-BC算法的第2代迭代開始，由于收縮因子a固定，算法“爆炸”產生的碎片解會很容易集中于一小片區域，而BB-BC算法的準確性取決于候選解的多樣性。雖然該問題可以通過增加候選碎片解的個數來解決，但該方法對計算機的運算能力有很大要求。所以本文將引入混沌邏輯映射的方法對傳統BB-BC算法進行改進。

3.1 一維混沌邏輯映射

混沌狀態是一種由確定性方程得到的具有隨機性的運動狀態，由于其具有隨機性、遍歷性以及規律性等特點，通常被用于優化算法之中。通過引入與優化變量個數相同的混沌變量，利用混沌系統的遍歷性，來改善優化變量的全局搜索能力。

對于本文所研究賽車的全程行駛策略問題，算法中每一代的解即為賽車的巡航速度。由于速度策略是1×n的矩陣，可以利用一維邏輯映射，將混沌狀態引入收縮因子at之中。一維邏輯映射的數學表達式為：

式中：·μ為邏輯映射參數，對于區間[0,1]上的at，·μ取值接近4時，邏輯映射將進入混沌狀態。此時式（7）改寫為：

為了不污染混沌變量，r相應地只取1或-1。

3.2 改進BB-BC算法實現

利用一維邏輯映射后，賽車的全程行駛策略優化算法實現流程如圖4所示。

圖4 改進BB-BC算法實現流程

4 模型參數試驗標定

由于電驅動系統建模已采用試驗測得的效率MAP圖進行，本文還需要對MPPT效率、電池Puekert系數以及整車能耗進行相關試驗標定，以保證模型的準確性。

4.1 MPPT效率特性測試

對MPPT進行不同光照強度下的效率特性測試。由圖5可知，MPPT 工作效率與工作時的功率相關，當功率較小或較大時效率低，功率適中時效率高，但總體相差不大，所以本文取MPPT效率為恒定值98%。

圖5 MPPT效率特性測試

4.2 電池Puekert系數測定

本車采用NCR18650B鋰離子電池，對電池單體進行恒功率放電測試，測試結果如圖6所示。測得實際容量3 207 mAh，根據式（6）計算得出該電池的Puekert系數為1.06。

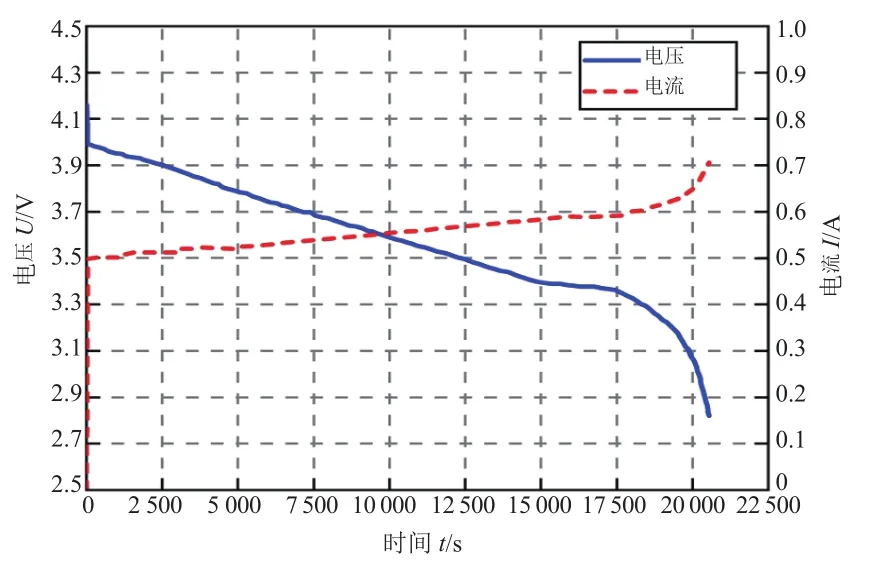
圖6 電池單體恒功率放電測試

4.3 整車模型驗證

整車能耗測試平臺如圖7所示，測試系統由德國IMC多通道數字采集儀、電流/電壓傳感器、無線網橋以及上位機組成。測試過程中整車實時能耗數據由多通道數字采集儀組網后通過無線網橋發送至位于數據采集車輛中的上位機，并由上位機軟件進行讀取、分析和數據記錄。

圖7 整車能耗測試平臺

由于太陽光照情況變數較大，只在純電池驅動下進行整車能耗試驗，測試0～80 km/h內的整車功率需求，試驗結果如下：

圖8 整車能耗測試結果對比

圖9 實車測試場景

由于實際試驗過程中，受側風、道路粗糙度以及電驅動系統實際工作效率等影響，實測功耗總體上要高于仿真值，尤其是低速區的差值較大。但在實際巡航速度區間仿真曲線與實測值基本一致，模型可以用于策略優化。

5 全程行駛策略優化

5.1 目標函數及約束條件

WSC賽事的比賽成績依據完賽時間、里程（針對未完成所有賽段的車隊）以及除太陽能以外的額外用電量等進行計算，其中完賽時間直接關系到比賽的排名，所以本文行駛策略的優化目標為賽車的總完賽時間，即目標函數為：

式中：T為總完賽時間；ti為完成每一區間所需的時間，比賽共10個區間。

優化過程中有以下約束條件：

（1）對于輪轂電機直驅賽車，其車速搜索空間的下界為60 km/h（根據最晚完賽時間計算），上界為最高設計時速130 km/h。

（2）比賽全程3 021 km，分為3個大賽段，除起點和終點外一共9個檢查站，用于強制停車休息，每天規定的比賽時間為8:00～17:00，檢查站強制停車時間為30 min。

（3）賽車的電池SOC約束值。

基于以上約束條件，單次模型仿真流程如圖10所示。優化過程中，參考速度為仿真模型的唯一輸入條件，通過模型計算出的完賽時間反饋至改進的BB-BC算法中，進行下一代速度的生成。優化過程直至達到最大迭代次數為止，最終得到最優的參考巡航速度以及完賽時間。

圖10 模型仿真流程

然而，并非所有速度策略都能完賽，因為速度過快會導致動力電池SOC降為0，觸發模型停止仿真。因此，僅僅將模型仿真時間作為性能指標是不合理的。在仿真計算時，對此種情況，依據停車地距離終點的距離，設置成比例的、較大量級的罰時，從而使模型優化解符合實際需求。算法的求解設置見表3。

表3 算法優化參數

5.2 全程行駛策略優化結果

5.2.1 全局尋優結果對比

為了說明改進BB-BC算法與BB-BC算法在尋優方面的差別，分別使用兩種算法針對賽車完賽時間進行全局尋優仿真，考慮實際計算中的計算機資源及時間成本，選擇迭代次數為25次，仿真收斂結果對比如圖11所示。可以看出，改進BB-BC算法的收斂速度相對較快，收斂曲線相對平穩，且最終優化結果（全程完賽時間）優于BB-BC算法，為40.16 h。而BB-BC在迭代過程中多次陷入局部最優值，若在前期沒有設置較大的迭代次數，很可能導致算法尋優提前終止，從而得不到最佳的行駛策略。

圖11 BB-BC算法與改進BB-BC算法仿真結果對比

5.2.2 全程行駛策略優化結果

利用改進BB-BC算法優化后的全賽段行駛策略結果如圖12所示。由圖可知，優化后的參考速度范圍為64～80 km/h，每一區間均對應一個優化速度。其中，在第5區間中參考速度最低，這是因為在該區間賽車將進入整個賽程中海拔最高的路段，道路平均坡度較大，出于能耗的考慮，策略中降低了賽車的行駛速度。

圖12 行駛策略優化結果

5.2.3 優化策略與常規策略結果對比

以第二大賽段為例，大多數車隊通常采用常規策略，即以一個固定巡航速度行駛。本文中常規策略選擇巡航速度為70 km/h。經過模型仿真，優化策略與常規策略結果對比見表4。

表4 優化策略與常規策略結果對比

由表4可知，采用優化策略行駛用時比常規策略縮短7.2%，可直接提高比賽排名和最終的成績得分。雖然優化策略在到達終點時電池能耗比常規策略略高，但16:30前當地太陽光照能量仍然可觀，賽車可在這段時間內充分利用太陽能為動力電池充電，以減少電池的額外充電量（車輛通過賽會提供的充電樁充電需要扣除相應的能耗得分），所以采用優化策略所導致的電池能耗的提高對比賽的最終成績無較大影響。

6 結論

針對輪轂電機直驅賽車，以WSC2019世界太陽能車挑戰賽為目標，建立整車優化模型。設計了改進的BB-BC算法對賽車行駛策略進行優化，得出以下結論：

（1）所建立的輪轂電機直驅賽車優化模型通過MPPT、動力電池測試以及實車道路測試結果比對，可以真實反映整車的能耗情況，具有良好的仿真精度。

（2）優化后的仿真結果表明，改進的BB-BC算法克服了傳統BB-BC算法在迭代中易陷入局部最優解的問題，其具有更快的收斂速度，且收斂曲線相對平穩，可以有效縮短賽車完賽時間。

（3）進行了優化策略的賽車實車驗證，在2019WSC賽事中，車隊采用優化后的行駛策略順利完成了第一賽段，結果表明了該方法的有效性。

（4）在后續的優化過程中可進一步考慮實際天氣、風向以及路況等因素，以提高優化精度。