軸承溫度對托索輪部件配合面變形的影響

黃 山 李 剛 閆登華 李 村 馬 胤

北京起重運輸機械設計研究院有限公司 北京 100007

0 引言

軸承是客運索道托壓索輪中的重要支撐基礎件，其能否安全穩定運行直接影響索道線路的安全性與可靠性。在索道檢修中,發現軸承在輪體內打滑的現象時有發生，造成這種現象的原因通常有配合選取不當、加工精度不高、結構運轉變形等因素。由于軸承在輪體中所處的環境較為封閉，散熱條件不佳，在較長時間高速運轉后，溫度不可避免地會升高，在載荷和溫度的雙重作用下，不僅影響軸承本身的性能，也會影響相關結構的配合精度，進而影響整體結構的功能和運行質量。

圖1 為托索輪結構示意圖，主要由輪體、軸承、夾板、端蓋、隔套等結構組成，當索道運行較長時間后，軸承溫度會升高，而從圖1 可以看到，軸承的散熱條件相對較差，由于軸承與輪體內圈和隔套均有配合要求，故需要考慮軸承溫升對各部件間配合的影響。

本文將通過對軸承發熱量的計算，在Ansys 中模擬得到其最高溫度，并將軸承作為熱源，分析常溫環境（20℃）下與軸承有配合關系的部件在受到溫度影響時的變形以及配合面接觸狀態的變化，為設計工作選取合理的公差配合提供參考。

圖1 托索輪結構示意圖

1 軸承摩擦與溫升計算

1.1 軸承摩擦力矩的近似計算

滾動軸承產生熱量的多少取決于軸承內的摩擦，而摩擦的大小受到包括軸承類型和尺寸、轉速、潤滑劑的特性和用量等因素的影響[1]。

軸承部件之間的滾動和滑動摩擦會阻礙軸承轉動，滾動體與滾道、保持架以及引導面之間的接觸均會產生摩擦阻力。此外，由于潤滑劑拖曳和接觸式密封件的存在也會產生摩擦。軸承的摩擦力矩為

式中：M 為軸承摩擦力矩，μ 為軸承摩擦系數，F為軸承載荷，d 為軸承內徑。

1.2 軸承的溫升

軸承摩擦損失在軸承內部幾乎都轉變為熱量，使軸承溫度上升，單位時間內摩擦產生的熱量為

式中：Q 為單位時間內的發熱量，M 為摩擦力矩，n 為軸承轉速。

1.3 軸承溫度的有限元計算

為便于計算，在有限元計算中省去了軸承的密封圈和保持架[2]，但在傳熱系數的設置上考慮了密封圈對散熱的影響。根據式（1）、式（2）計算得到軸承單位時間內的發熱量Q=8 W，如圖2 所示，（a）為軸承模型，（b）為軸承溫度云圖，最高溫度可達80℃。

圖2 軸承模型和溫度云圖

由圖2 可知，在散熱條件受限的情況下，軸承內外圈最高溫度均接近整體的最高溫度，因此在整個輪體計算中，可將軸承設置為一個恒溫熱源，分析其溫度大小對托索輪其他結構的影響。

2 溫度對各部件變形影響

圖3 為托索輪結構示意圖，模型中包含了與軸承直接接觸的輪體和隔套（以一根實心軸代替）。輪體材料為ZL104，其余結構材料為鋼。ZL104 合金密度2 650 kg/m3，20℃～100℃時的線膨脹系數為24×10-6℃-1，鋼的線脹系數為12×10-6℃-1。

圖3 整體模型示意圖

2.1 部件計算

首先單獨計算輪體、軸承和軸在常溫環境（20℃）下升溫過程（溫度梯度設為10℃）中的變形情況，如圖4 所示。

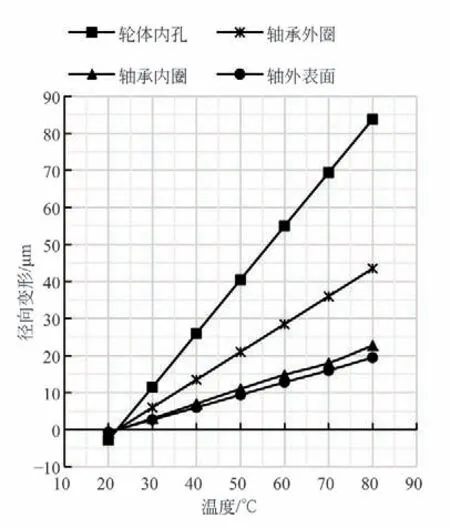
圖4 各部件單獨計算時的徑向變形

由圖4 可知，隨著溫度的升高，各部件徑向變形逐漸增加，各配合面中，輪體內孔變形最大，軸的外表面變形最小，軸承外圈變形大于內圈。由于輪體材料的線膨脹系數較鋼材大，故輪體內孔徑向變形較大。

為對比輪體內圈厚度對徑向變形的影響，建立不同內圈厚度的輪體模型，計算其徑向變形，如圖5 所示。

圖5 輪體內圈不同厚度下的徑向變形

由圖5 可知，改變輪體內圈厚度對其徑向變形的影響很小，可以忽略不計，故不再考慮輪體內圈厚度對其徑向變形的影響。

2.2 整體計算與單獨計算的對比

將輪體、軸承和軸進行整體計算時，需在各配合面設置初始過盈量，分別查看各件的徑向變形和剩余過盈量。

圖6 輪體內孔徑向變形對比

圖7 軸外表面徑向變形對比

由圖6 和圖7 可知，隨著溫度升高，輪體內孔和軸外表面的徑向變形均逐漸增大，單獨計算時變形量線性變化，整體計算時波動上升，但最終逐漸趨于一致，兩種計算方式的結果差異不大。

圖8 軸承內外圈徑向變形對比

由圖8 可知，軸承內外圈在不同計算條件的徑向變形差異較大，單獨計算時變形量線性變化，整體計算時波動上升，且內外圈整體計算中的徑向變形比單獨計算要大。

可知，過盈狀態的內外圈的初始變形量均比自由狀態下內外圈的初始變形量要大，這是由于整體計算時，軸承內外圈均處于過盈配合狀態，受到較強的擠壓作用，而輪體材料受熱后發生膨脹變形，與軸承的過盈配合發生變化，部分區域變成過渡配合甚至間隙配合，導致軸承約束減少，徑向變形量增加。

圖9 升溫過程中配合面過盈量變化

由圖9 可知，輪體內孔變形較大，隨著溫度的升高，與軸承外圈的過盈量逐漸減少。如圖10 所示，提取軸承外圈與輪體內孔的接觸壓力，可知大部分區域的接觸壓力很低，甚至為零，說明軸承外圈與輪體內孔的配合區域已經變成過渡配合甚至間隙配合。

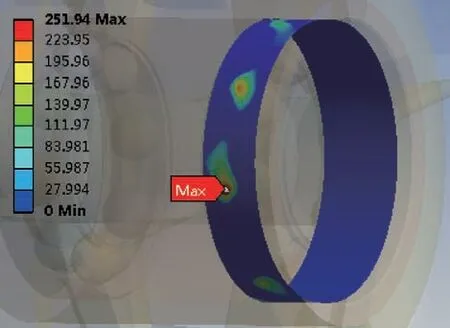
圖10 軸承外圈與輪體內孔接觸壓力

3 裝配間隙的計算

由上述分析可知由于不同材料的線膨脹系數不同，受熱時的變形量也不同，而尺寸的公差配合是以20℃為基準進行標注的，所以如果結合件材料的線脹系數不同，則需對各件之間的配合間隙（或過盈）進行修正計算，以選擇比較正確的配合類別[1]。計算公式為

式中：xzmax、xzmin為裝配間隙的最大值和最小值，tk、tz為孔和軸的工作溫度，xGmax、xGmin為工作間隙的最大值與最小值，t 為裝配時的環境溫度，d 為公稱直徑，ak、az為孔和軸的線脹系數，負號用于溫度提高導致孔的尺寸增大的情況，正號用于溫度提高導致孔的尺寸縮小的情況。

4 結論

不同材料的線膨脹系數不同，導致受熱時的變形量不同，從而影響配合精度。如果配合面會受到溫度變化的影響，則應盡可能使有配合的部位使用同種材料，使配合面的變形盡量一致，避免對配合精度造成過大影響。若不可避免的使用不同材料進行配合，則在結構設計時需要考慮溫度對公差配合的影響，并對配合間隙（過盈）進行合理的修正。