制造業集聚與生產效率:新證據與新機制?

王立勇 呂 政

(1.中央財經大學國際經濟與貿易學院 北京 102206)

(2.中央財經大學統計與數學學院 北京 102206)

一、問 題 提 出

中國經濟進入“新常態”以來，在美國金融危機的不利影響和中國自發進行供給側結構性改革的綜合作用下，經濟增速逐年下滑，經濟增長下行壓力較大，中長期經濟發展潛力以及長期經濟增長已成為人們越來越關注的問題。新古典經濟增長理論認為，一個經濟體的長期經濟增長主要倚靠生產率的提高。特別地，隨著近年來中國就業人口出現下滑、老齡化程度逐漸加重，人口紅利日漸消弭，這使提高生產效率變得更加迫切和關鍵。黨的十九大報告指出:“中國經濟已由高速增長階段轉向高質量發展階段，正處在轉變發展方式、優化經濟結構、轉換增長動力的攻關期”，“必須堅持質量第一、效益優先，以供給側結構性改革為主線，推動經濟發展質量變革、效率變革、動力變革，提高全要素生產率”。由此可見，提高生產效率是高質量發展的動力源泉，對于中國跨越中等收入陷阱、全面建設社會主義現代化國家具有重要意義。

如何才能提高生產效率呢? 梳理既有文獻不難發現，影響生產效率的因素眾多，而產業集聚被認為是相對重要的一項。作為產業集聚的重要內容，制造業集聚的過程及其影響越來越受到學界和業界的關注。鑒于問題的重要性，國內外已有文獻對產業集聚與生產效率的關系進行了廣泛且深入的探討，但并未得到一致結論，相關研究大體分為三類:第一類文獻認為產業集聚有利于提高生產效率。持此類觀點的研究認為，企業受益于產業集聚帶來的規模經濟，在正外部性的作用下提高了生產效率(王永進和張國峰，2016；張國峰等，2017)。第二類文獻認為產業集聚不利于提高生產效率。該類文獻認為，產業集聚容易引起交通擁堵及通勤成本上升、土地及勞動力要素成本上升、居住與生活成本上升等負外部性經濟影響，進而惡化企業生產效率(盛丹和張國峰，2019；趙瑞麗等，2019)。第三類文獻認為產業集聚與生產效率之間存在非線性關系。Broersma 和Oosterhaven (2009) 的研究結果顯示，產業集聚對生產效率的擁擠效應將先于集聚效應出現，并且負向的擁擠效應和正向的集聚效應均會為相鄰地區的集聚水平所弱化。沈能等(2014) 將產業集聚度設為門檻變量，運用門檻模型檢驗了制造業集聚對生產效率的非線性影響。值得關注的是，Desmet 和Fafchamps (2005)、余泳澤等(2016) 結合地理因素分析了產業集聚對生產效率的空間外溢效應，在不同地理邊界上考察空間溢出的非線性特征，實證檢驗了產業集聚與生產率之間的非線性關系受到除集聚本身以外的因素影響。

考慮到中國問題的特殊性，產業集聚對勞動生產率的影響相對復雜，已有文獻直接得出二者正相關或負相關的結論均可能存在偏差。圖1 和圖2 分別給出了路網相對稀疏的福建、貴州、陜西、寧夏四地和路網相對稠密的天津、浙江、安徽、河南四地的制造業集聚與生產效率之間的散點圖。圖1 中，地處我國東南、西南、西北地區的福建、貴州、陜西、寧夏地形以山地、丘陵為主，交通運輸條件先天不足。圖2 中，地處我國東部、中部地區的天津、浙江、安徽、河南地形以平原為主，交通條件相對發達。對比圖1 和圖2 可以明顯看出，制造業集聚與生產效率之間分別呈現“一反”和“一正”的相關性:在路網相對稀疏的地區，制造業集聚與生產效率之間呈負相關；在路網較為稠密的地區，制造業集聚與生產效率之間呈正相關。直觀地看，制造業集聚與生產效率之間的關系可能與交通運輸條件相關，當交通運輸條件較差時，制造業集聚與生產效率存在負相關關系，而當交通運輸條件較好時，二者之間存在正相關關系。這一現象是已有文獻所未發現且無法解釋的，但此處僅僅是給出初步證據，是否具有一般性，還有待進一步論證和檢驗。

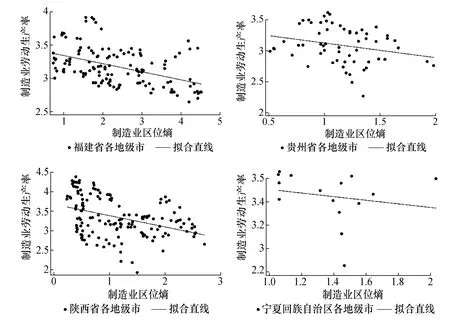
圖1 2003—2017 年福建、貴州、陜西、寧夏四地制造業集聚與生產效率的散點圖

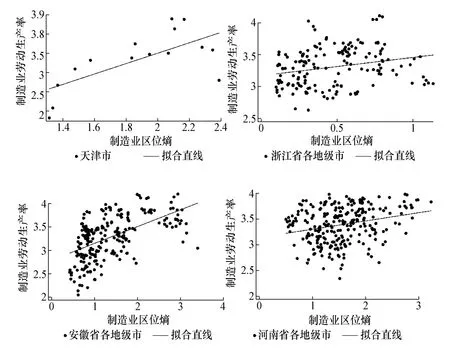
圖2 2003—2017 年天津、浙江、安徽、河南四地制造業集聚與生產效率的散點圖

與已有文獻相比，本文創造性工作主要體現在:第一，研究視角的創新。本文引入交通運輸條件，從理論與實證兩方面分析在不同交通運輸條件下制造業集聚對生產效率存在的異質性因果效應，以更好地解釋經濟現實。與以往非線性關系的研究不同，Broersma 和Oosterhaven (2009)、沈能等(2014) 檢驗的是伴隨產業集聚水平不斷提高，由產業集聚自身變動對生產效率帶來的非線性影響，并未考慮其他因素可能帶來的外部性；Desmet 和Fafchamps (2005)、余泳澤等(2016) 基于地理距離檢驗產業集聚對生產效率的空間非線性效應，即隨著地理距離的延伸，產業集聚對生產效率存在非線性影響，在研究中并未側重考慮交通運輸條件問題，與本文研究存在較大差異。本文重點討論交通運輸條件在產業集聚與生產效率之間非線性關系中起到的作用。第二，理論方面的創新。本文在納入交通運輸成本的基礎上，構建能夠刻畫制造業集聚與生產效率之間關系的兩部門經濟模型，通過求解壟斷競爭下的一般均衡結果分析交通條件在制造業集聚與生產效率中發揮的作用。第三，在研究方法上，考慮到制造業集聚與生產效率之間可能存在的非線性關系，本文放松線性約束，借助門檻面板模型內生劃分不同交通運輸條件情況，以檢驗不同交通運輸條件下制造業集聚對生產效率的非線性影響，彌補已有研究的不足，提供新的經驗證據。第四，在指標測度方面，鑒于傳統勞動生產率的計算方法未考慮各城市制造業發展階段的差異，只是簡單地用總產值除以就業人數，導致不同制造業規模的城市之間缺乏可比性，本文進一步測算了各城市之間可比的制造業勞動力績效，以度量制造業生產效率，為后續相關研究提供參考指標。

其余部分結構安排如下:第二部分為理論分析框架；第三部分是實證設計；第四部分為實證檢驗結果；最后是本文的研究結論與政策建議。

二、理論分析框架

為厘清不同交通運輸條件下，制造業集聚對其生產效率影響的作用機制，本文以Abdel-Rahman 和Fujita (1990)、Duranton 和Puga (2005) 的中間產品模型為依據，參考Ciccone 和Hall (1996) 的單位面積需求成本思想，在一個納入運輸成本的兩部門模型中進行理論分析。

首先，本文做出如下理論假設:第一，模型經濟為制造業(x) 和零售業(y) 構成的兩部門經濟，分別作為產業鏈的生產端和銷售端，所有廠商的區位選擇不受限制。第二，市場形式屬于壟斷競爭，制造商利用勞動和資本要素生產有差異產品，零售商利用勞動力和制造商提供的中間產品向消費者提供有差異服務。第三，城市中的所有廠商呈線性均勻分布。第四，要素和產品的自由流動需要一定運輸成本。運輸成本ε取決于當地的土地面積S以及交通運輸條件h，將運輸成本表示為:

用CES 效用函數刻畫不同城市的消費者偏好，零售業商品的不變替代彈性σr＞1，用Ei和Ej表示城市i和城市j中消費者對零售品的總支出，對應地用Ir，i和Ir，j分別表示兩個城市商品市場的價格指數，pr，i(y)為零售商的商品銷售價格。參考柯善咨和趙曜(2014) 的做法，將城市i中單個零售商的需求函數設為:

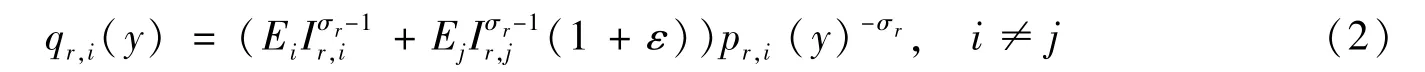
將零售商需求轉換成單位面積需求，并用單位需求密度函數表示；另外，假設需求密度的彈性系數為(λ-1)/λ，其中λ＞1。ei和ej表示單位面積上城市i和城市j的消費者對零售商品的支出，qr，i(y)/Si為零售商的單位面積需求，則單個零售商的單位面積需求密度為:

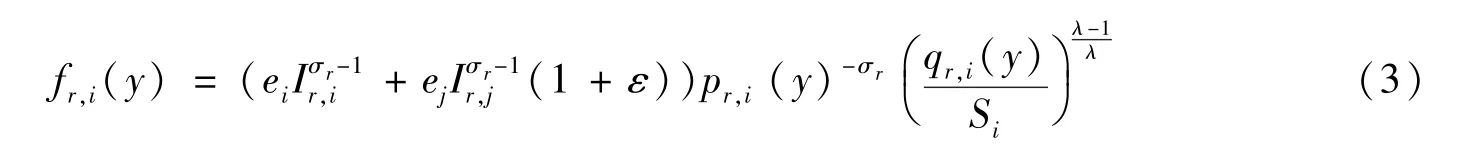
根據廠商線性均勻分布的假設，有:

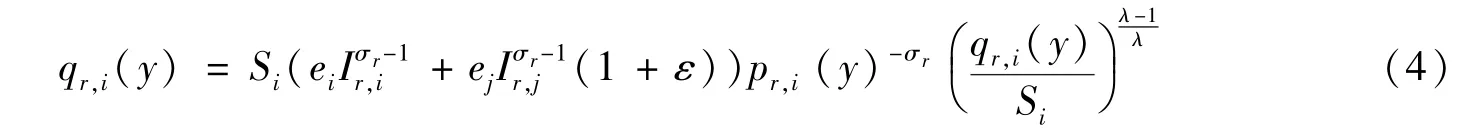
提取公因式qr，i(y)/Si，將零售商的單位面積需求函數變形為:

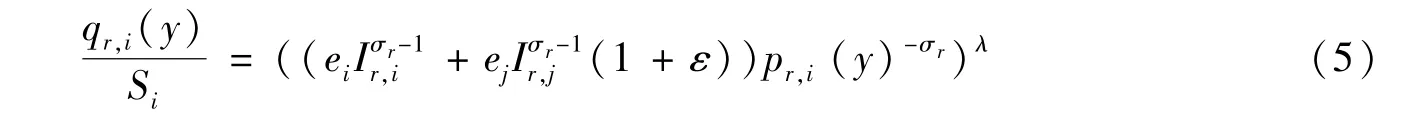
假定零售商的可變成本和固定成本分別為cvr，i和cfr，i，wi代表銷售過程中向勞動力支付的工資，Im，i代表上游制造業產品的價格指數，β是制造業產品占投入成本的比重。為體現運輸成本在要素轉移中發揮的作用，本文將運輸成本歸結到制造業中間產品成本中，運輸成本越高，中間產品投入在零售商成本中的比例越高，用β/(1 -ε)表示中間品投入份額，因此單個零售商的成本函數及其單位面積成本函數分別設為:

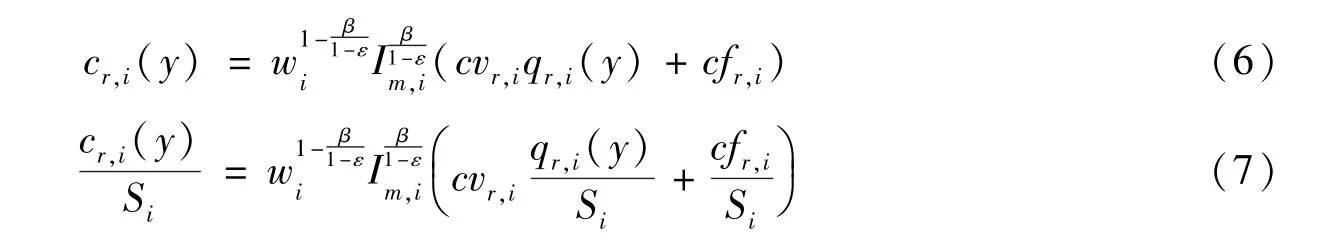
類似地，假設制造商生產的中間品的不變替代彈性為σm＞1，用Xi表示城市i的制造商總數，則制造業產品的價格指數為:

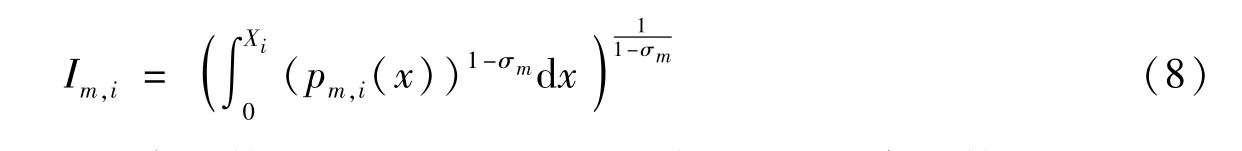
同理，制造商的單位面積需求函數見式(9)，Yi表示城市i的零售商總數:

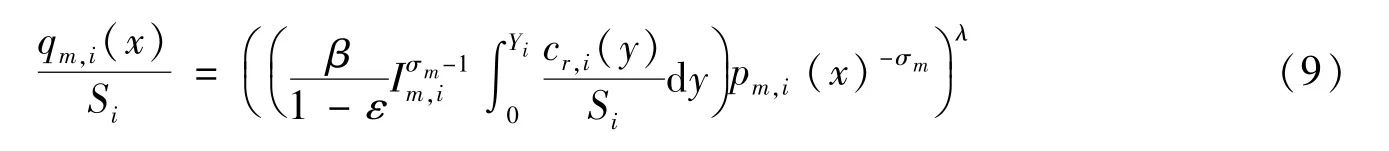
同樣令制造商的可變成本和固定成本分別為cvm，i和cfm，i，制造商在生產過程中需要投入勞動力和資本，用ki表示原始資本投入的利息，賦予資本的權重為δ，并納入運輸成本的影響，得到制造商單位面積成本函數:

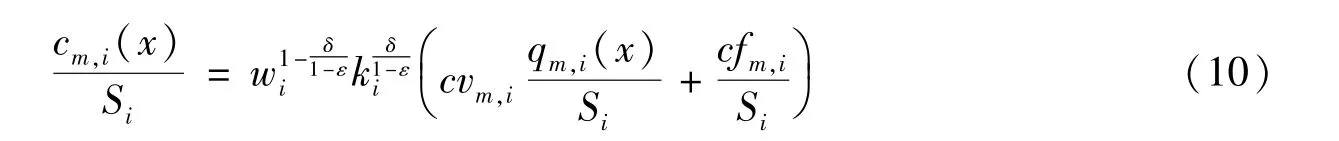
在壟斷競爭的市場形式下，求解廠商的一般均衡結果分兩步①因篇幅所限，本文省略了一般均衡求解的具體推導過程，感興趣的讀者可在《經濟科學》 官網論文頁面“附錄與擴展”欄目下載，具體見第一部分。:第一步，在短期所有制造商實現利潤最大化。通過關于零售商的式(5) 和式(7)，關于制造業的式(9)和式(10)，本文分別利用利潤最大化的一階條件，得到均衡時零售業和制造業的最優定價。第二步，在長期廠商可以自由進出市場，在長期中任一企業的利潤必須為零，得到零售商和制造商長期均衡下的單位面積需求qr，i/Si和qm，i/Si。結合兩部門的產出關系，得到制造業在城市i的最優產量為:

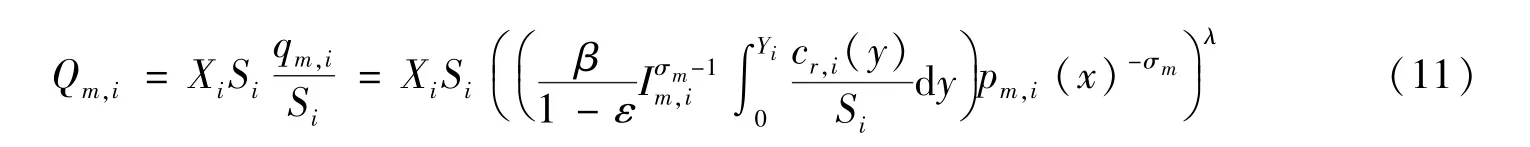
為了與代表性研究保持一致，參考Ciccone 和Hall (1996)、Kanemoto 等(1996)、柯善咨和趙曜(2014) 用人均產出衡量生產效率的做法，以及Ciccone 和Hall (1996)、孫曉華等(2017) 用勞動力與城市面積的比值測度集聚水平的方法，本文以制造業產量與制造業就業人數的比值Qm，i/Lm，i衡量制造業勞動生產率，以制造業就業人數與城市面積的比值Lm，i/Si衡量制造業集聚水平，同時將wi、ki、Yi和qr，i視為控制變量，其他變量作為常數，得到制造業生產效率與制造業集聚的函數關系為:

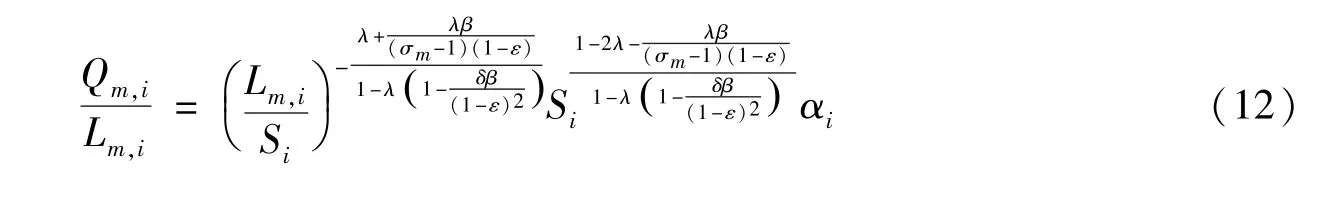
對式(12)①中的制造業集聚Lm，i/Si求一階導數，可得到制造業集聚對其生產效率的影響，求導結果如下:

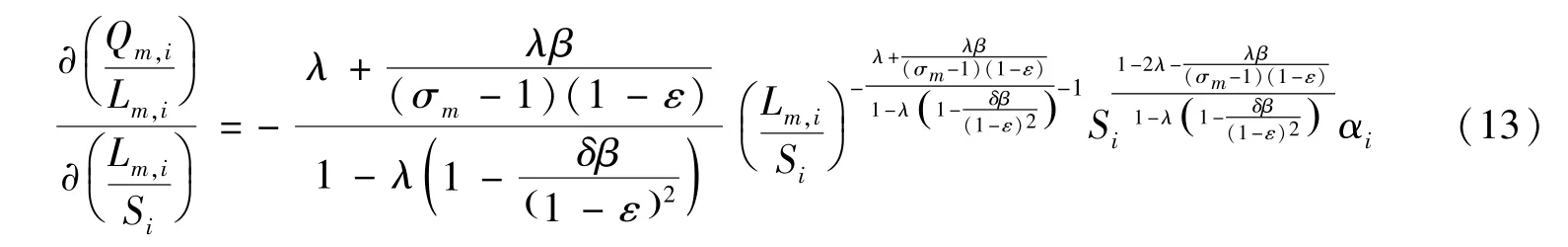
由上述數理模型的推導結果可知，隨著運輸成本的不斷降低，制造業集聚與生產效率之間呈現出U 形的非對稱關系，拐點的位置取決于運輸成本系數。如果運輸成本大于臨界值，那么制造業集聚會阻礙生產效率提高，只有當運輸成本小于臨界值時，制造業集聚才會發揮出應有的規模經濟，對生產效率起到促進作用。可見，交通運輸條件會在制造業集聚與制造業生產效率的關系中具有重要影響，本文認為引入交通運輸條件后，制造業集聚對生產效率非線性影響的作用機制如下:

綜合新經濟地理學的理論假設以及中國制造業集聚的動力來源分析可發現，制造業集聚看似是一種宏觀經濟表現，實質上是制造業企業的微觀區位選擇，且選址過程在現實經濟中受多方面因素影響，交通區位優勢是促成地方制造業集聚的一個重要原因，但也不排除負外部性的可能(白萬平等，2019)。

一般而言，制造業企業的運輸成本會隨著交通運輸條件的改善而下降，擁有交通區位優勢的地區，會吸引生產關系前后關聯的制造業企業自發地聚集到一起。同一類型或不同類型的制造業企業在一定區域范圍集聚時，不僅實現了專業化的勞動、資本集中，還傳播了生產技術和管理經驗(戴美虹，2020)。在MAR 外部性和Jacobs 外部性的綜合作用下，正向的集聚效應為制造業生產帶來了規模報酬遞增的效果，有力地提高了制造業生產效率。通過文獻梳理可知，有經驗證據顯示在擁擠效應下，制造業集聚會對生產效率帶來負面影響。需要說明的是，擁擠效應是指制造業企業在從事生產活動時，生產要素的投入存在一個最優比例，如果制造業企業在工業園區過度集中，企業數量超過了園區的承載能力，為了自身利益最大化，會出現對勞動、資本、土地、原材料、公共基礎設施等資源的爭奪，過度的競爭會導致生產要素配置不平衡，造成制造業生產效率的損失(梅林和席強敏，2018)。在制造業集聚的過程中，負向的擁擠效應與正向的集聚效應同時產生，在不同均衡狀態下這兩股力量的作用大小有所不同，并且擁擠效應和集聚效應的強度可能會隨當地其他環境因素的改變而改變。結合本文數理模型的推導結果可以判斷，這些環境因素恰好包括本文所關注的交通運輸條件。具體來說，在交通運輸條件薄弱的地區，自身的經濟體量往往相對有限，當地的制造業集聚程度在全國范圍內處于較低水平，制造業集聚帶來的正向效應并沒有理想地發揮出來。此外，在這些不具備交通區位優勢的地區，制造業集聚的形成還帶有較強的政府主導特點，當地的工業園區在招商引資時得到了政府給予的大量政策優惠。在政府牽頭下形成的制造業集聚，并不是由當地區位優勢自發形成的，集聚效應往往不強。隨著制造業企業不斷進駐工業園區，擁擠效應將占據主導地位，反而不利于提高生產效率，失去了原先制定產業政策的應有之義。

綜上所述，在交通運輸條件作用下，制造業集聚對生產效率的影響是一柄“雙刃劍”，既可能引起負向的擁擠效應對生產效率造成損失，也可以利用正向的集聚效應提高生產效率，制造業集聚對生產效率的影響本質上取決于上述兩股力量孰強孰弱。本文認為，當制造業集聚引起生產要素配置失衡時，為弱化擁擠效應對制造業生產效率帶來的負面影響，需要優化當地生產要素配置，而交通運輸條件在其中發揮著重要作用。隨著交通運輸條件不斷完善，當地的經濟承載能力將相應提高，隨著生產要素配置不斷優化，制造業集聚帶來的擁擠效應主導會逐漸向集聚效應主導轉變，進而對生產效率帶來積極影響。

經過上述數理推導和理論機制分析，本文提出以下兩個待實證檢驗的研究假說:

假說1:制造業集聚對生產效率具有非線性影響。

假說2:制造業集聚對生產效率的作用方向取決于交通運輸條件。

三、實 證 設 計

本部分介紹選用的研究方法，構建與數理模型推導相匹配的計量經濟模型，并對變量含義與數據來源進行說明。

(一) 研究方法和模型設定

根據前述理論分析框架的一般均衡結果，為驗證研究假說，本文在此借助門檻面板模型對制造業集聚與生產效率的關系進行實證檢驗。該方法以樣本數據為依據，能夠客觀地估計出交通運輸條件(門檻變量) 的閾值，避免了以往按均值或分位數主觀分組檢驗造成的偏誤。該方法的主旨思想是根據樣本數據，內生估計出交通運輸條件的門檻值，從而劃分交通運輸條件優劣區間，將制造業集聚設為隨該區間而變的解釋變量，通過構建分段函數進行分組回歸，并對該門檻值的“門檻效應”進行相應檢驗。門檻面板模型設定為:

式(14) 中，i表示城市，t表示年份，LNLPit、LQit和ROADit分別表示制造業勞動生產率、制造業集聚和交通運輸條件，其中ROADit是根據數理推導選定的門檻變量，LQit是核心解釋變量。為了避免由于遺漏變量偏差導致的內生性問題，本文在模型中增加了控制變量，用Xit表示，β是待估系數，εit為隨機擾動項，γ為待估計的門檻值，I(·)為指示函數，當滿足括號內的條件時，令I＝1，反之，I＝0。

(二) 變量定義和數據說明

1.被解釋變量

目前關于生產效率的測度方法主要有三種，分別是Malmquist 指數、全要素生產率(TFP)、勞動生產率。綜合考慮地級市層面數據的可得性，以及指標選取的代表性，本文最終選取勞動生產率(LNLP) 反映制造業生產效率。另外，在穩健性檢驗中，本文測算了制造業勞動力績效(PL) 作為勞動生產率的度量指標，以反映生產效率的相對質量，計算方式如下:

式(15) 中，Yit和Lit分別表示第i個城市在t年份的工業總產值及其總就業人數。

2.核心解釋變量和控制變量

關于制造業集聚水平的測度方法較為豐富，本文采用區位熵(LQ) 衡量制造業集聚，該指標簡單易行，較好地刻畫了各個城市制造業集聚的相對水平，計算方式如下:

式(16) 中，EMit和Eit分別表示第i個城市在t年份的制造業就業人數及全行業就業總人數。在穩健性檢驗中，本文參考孫曉華等(2017) 的做法，測算了就業密度，以反映制造業生產活動的空間分布情況。在控制變量選取方面，本文采用投資依存度(INVEST) 來控制固定資本投資規模對制造業勞動生產率的影響；利用FDI 占GDP 比重衡量外資滲透度(FDI)；采用財政支出(EXPEND) 衡量政府對市場的干預程度，且政府財政支出的增加會提高企業的稅收負擔；采用職工平均工資反映消費能力(WAGE)，平均工資越高，消費者的購買能力越強，對制造業產品的需求往往更高；采用出口依存度(EXPORT) 控制出口導向對制造業生產效率的影響。需要說明的是，很多學者在省際問題的研究中，把鐵路當作交通基礎設施的代理變量，鑒于地級市層面的鐵路里程數據較難搜集，因此本文采用公路密度(ROAD) 衡量各城市的交通運輸條件。

3.數據來源

本文搜集整理了2003—2017 年中國286 個地級及以上城市的樣本數據，數據主要來源于《中國城市統計年鑒》、《中國區域經濟統計年鑒》 以及各省市統計年鑒，利用插值法補齊個別缺失數據，實際樣本記錄為4 290 組。另外，在2011—2013 年，國務院撤銷了安徽省的巢湖市，將其轄區歸入合肥、蕪湖和馬鞍山三市，升格貴州省畢節、銅仁兩個地級市，在海南省設立三沙市，在青海省設立海東市，因此地級及以上城市數量由287個變為290 個，為統一口徑，本文剔除了畢節、銅仁、三沙和海東4 個地級市進行實證分析。價格指數來源于2003 年以來各省市統計年鑒，所有貨幣價值的數據以2003 年不變價進行平減，并給出變量定義及各變量的描述性統計結果。①變量定義與描述性統計請見《經濟科學》 官網“附錄與擴展”第二部分。

四、實 證 結果

本部分將給出實證分析結果，并從替換被解釋變量、替換核心解釋變量和內生性等方面進行相應的穩健性檢驗。

(一) 門檻效應檢驗

進行門檻回歸前，本文首先檢驗是否存在門檻效應，并判斷模型中存在的門檻個數，利用拔靴法反復抽樣300 次得到的檢驗結果見表1。由表1 可知，僅單一門檻的p值小于1%，意味著交通運輸條件存在“單門檻效應”，門檻值為0.19，其95%的置信區間為[0.18，0.20]。

表1 交通基礎設施門檻效應檢驗結果

(二) 門檻面板數據模型估計結果

表2 報告了基于單門檻效應的門檻面板模型檢驗結果，可以看出，在制造業區位熵與勞動生產率的關系中，交通基礎設施的門檻效應十分明顯。表2 中的第(2) 列至第(5) 列是在第(1) 列基礎上逐步加入外商直接投資、財政支出、出口依存度和平均工資后，檢驗了制造業區位熵對制造業勞動生產率的非線性影響。從各列結果可知，當控制了關鍵控制變量之后，核心解釋變量區位熵系數估計結果的方向、大小和統計顯著性并未發生明顯變化，說明本文核心解釋變量系數的估計結果是穩健的。

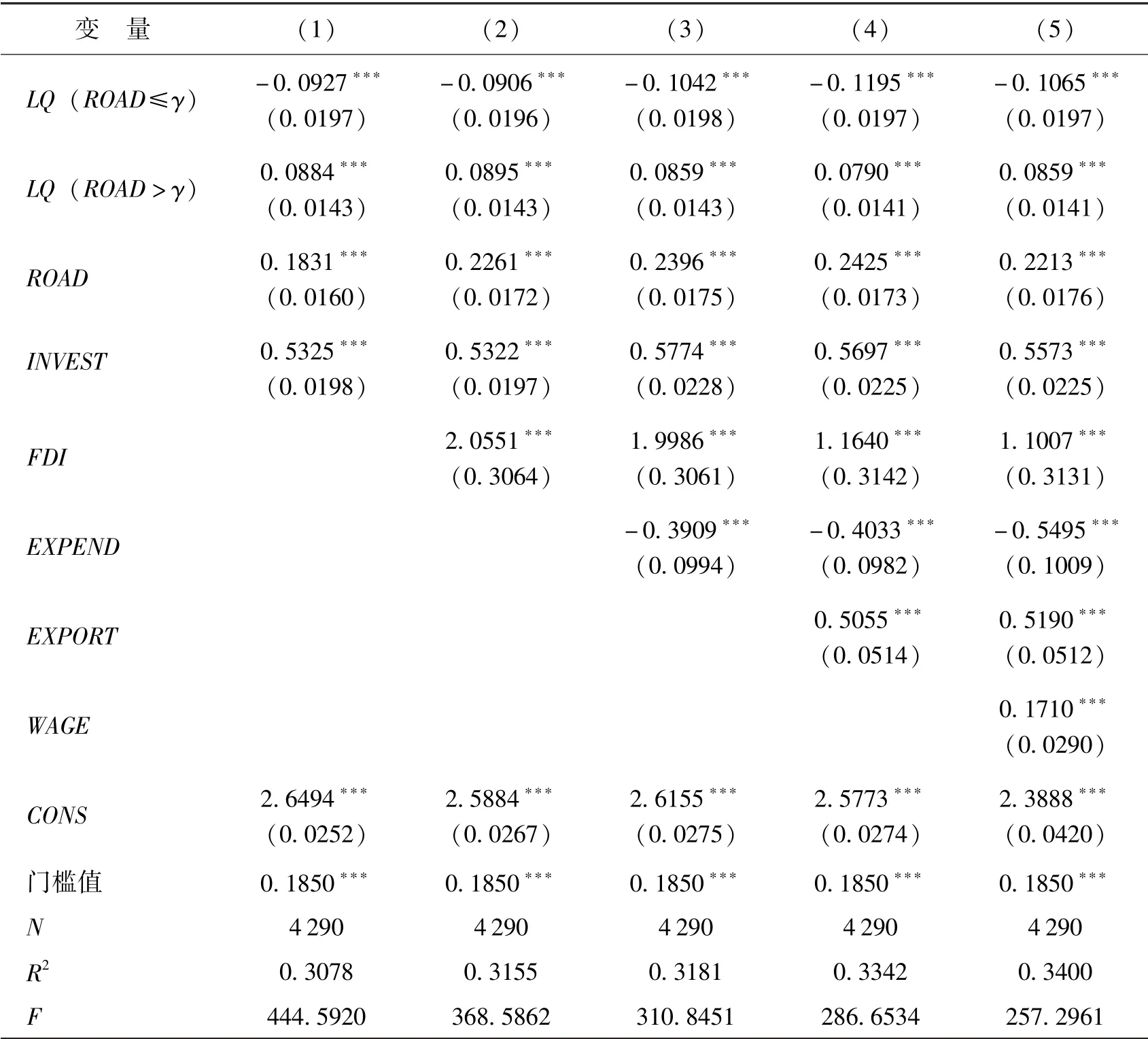
表2 門檻面板數據模型估計結果

從表2 可以看出，在交通運輸條件門檻值劃分的兩個區間上，制造業集聚對生產效率的影響存在明顯差異。當地級市的公路密度小于等于0.19 時，即對交通運輸條件較差的地級市而言，制造業集聚對勞動生產率的影響顯著為負，這說明在制造業集聚形成的初期，大量的就業、資金涌入城市，但沒有相應的交通基礎設施與之相匹配，產業集聚在短期造成了城市人口規模擴張、交通堵塞及通勤成本上升等后果，使生產要素的流動受到一定限制，制造業集聚對生產效率的擁擠效應較為強烈，阻礙了資源利用效率的最大化，難以有效發揮制造業集聚的規模經濟，不利于生產效率的提高。在擁擠效應為主要影響時，按照原先的制造業發展模式，制造業企業繼續大量集中會加劇擁擠效應，因此有必要改善交通基礎設施。當城市公路密度大于0.19 時，交通運輸條件得到改善，此時制造業集聚產生的集聚效應更強，集聚效應接替擁擠效應占據主導地位，制造業集聚對生產效率正向的促進作用開始顯現。在現實經濟中，當交通基礎設施改善到一定程度時，制造業企業能夠共享基礎設施，工業園區中的制造業企業通過專業化分工、產業前后向關聯、規模化采購以及共擔風險的方式獲得規模報酬遞增帶來的正外部性，進而提高制造業生產率。上述實證分析結果與理論分析結論完全吻合，制造業集聚在不同的交通運輸條件下對生產效率的影響存在顯著差異，驗證了制造業集聚與生產效率之間存在非線性關系。

表2 估計結果還顯示，公路密度的估計系數顯著為正，說明改善交通運輸條件、降低運輸成本，有利于廠商建立穩定的供銷關系，促進生產率的提高。投資依存度對生產效率具有顯著的正向影響，即投資環境改善會提高生產率。值得注意的是，無論是統計意義還是經濟意義，FDI 對生產效率都有顯著的促進作用。FDI 作為知識與技術的載體，通過技術外溢的方式提升企業的創新能力，大幅提高了制造業生產效率。

(三) 穩健性檢驗

本文主要從三個方面進行穩健性檢驗。①因篇幅所限，本文在這里僅說明穩健性檢驗的方法，穩健性檢驗部分的詳細內容請見《經濟科學》官網“附錄與擴展”第三部分。第一，替換被解釋變量的穩健性檢驗。考慮到制造業生產效率測度指標的不同選擇，能夠從不同角度反映制造業集聚對生產效率的影響，同時為了減少用勞動生產率衡量生產效率可能存在的度量誤差，本文利用勞動力績效作為生產效率的衡量方法進行穩健性檢驗，相對于勞動生產率側重絕對數量，勞動力績效側重于比較各個地級市生產效率的相對高低，盡可能弱化各城市之間制造業規模上的差異，強調比較生產效率質量的相對高低。第二，替換核心解釋變量的穩健性檢驗。本文采用就業密度指標替代原先的區位熵，以更好地反映制造業生產活動的空間分布情況。第三，內生性討論。本文雖然在模型中控制了一系列變量，但模型仍可能存在雙向因果關系等導致的內生性問題，本文對此進行討論。上述穩健性檢驗結果充分證明了上文結論的穩健性和可信度。

五、結論與建議

為厘清交通運輸條件在制造業集聚與生產效率的關系中發揮的作用，以及制造業集聚對生產效率的影響機理與作用路徑，本文在中間產品模型基礎上，將運輸成本納入刻畫制造業集聚與生產效率之間關系的兩部門經濟模型，從理論層面分析制造業集聚與生產效率之間的非線性關系。隨后，本文以2003—2017 年中國286 個地級及以上城市的平衡面板數據為樣本，借助門檻面板模型實證檢驗在不同交通運輸條件下制造業集聚對生產效率的非線性影響，得到以下結論:第一，制造業集聚對生產效率的影響存在門檻效應，且該影響受交通運輸條件這一門檻變量影響。以公路密度的門檻值為界，將樣本劃分為交通運輸條件發達和欠發達地區，當公路密度跨越門檻值時，制造業集聚對生產效率的影響存在顯著的由負轉正的變化。第二，制造業集聚能否促進生產效率提高，主要取決于集聚效應和擁擠效應二者的相對強弱。在交通運輸條件發達的地區，制造業集聚帶來的集聚效應強于擁擠效應，有利于提高當地的生產效率。反之，在交通運輸條件薄弱的地區，制造業集聚的擁擠效應更強，對生產效率難以產生促進作用。第三，FDI 的技術外溢對提高制造業生產效率的成效顯著。對比實證檢驗結果，無論是以絕對數量還是以相對質量衡量制造業生產效率，FDI 都能有效刺激生產效率的提高，在質量方面的刺激作用尤為明顯，意味著作為知識和技術載體的FDI 具有顯著的技術外溢。

基于上述研究結論，本文提出如下政策建議:第一，加強交通基礎設施和配套環境建設，避免一擁而上或盲目地推進工業園區和產業園區建設。當地政府應當為提高生產效率創造良好的外部環境，依據地區的產業級差，借助市場力量合理有序引導產業轉移，加快欠發達地區的工業化進程，從而獲取集聚優勢。第二，因地制宜引導制造業集群發展，提升制造業產業鏈高端布局比重，助力制造業高質量發展。在經濟增長下行壓力增大的挑戰下，中國制造業亟待變“要素驅動”為“創新驅動”，實現制造業轉型升級。第三，重視引進外資，消除生產要素流動壁壘，以推動制造業集聚和高效發展。制造業空間布局失衡導致大量生產資源的閑置和浪費，建議在效率優先兼顧公平的原則下，通過市場競爭和梯度發展，由粗放型增長向集約型增長方式轉變。