混合儲能系統分散自適應強扭曲虛擬阻抗控制

單鎖蘭，谷志鋒，李宏城，高 升，劉雅芳，劉靖波

(石家莊鐵道大學電氣與電子工程學院，河北 石家莊 050043)

0 引 言

隨著鋰電池組（cell array，CA）能量密度、超級電容(super capacitor,SC)功率密度不斷提升，以及電能變換技術的不斷進步，由CA和SC構成一類重要的混合儲能系統（HESS）。HESS系統由于可以有效抑制負載功率大范圍、瞬時波動，所以在新能源微電、電動汽車、軌道交通等領域有著廣泛應用[1-2]，同時HESS分散穩定控制技術是眾多學者關注的重點。

HESS分散控制的核心是儲能變換器（雙向DC/DC）的并聯控制技術[3]。為解決儲能變換器因含大量電力電子器件所呈現非線性問題，許多學者在DC/DC變換器非線性穩定控制方面做了大量研究。在低頻小信號模型下，儲能變換器可簡化為平均狀態線性模型，并采用傳統線性控制方法[4]可實現系統穩定。文獻[5]采用傳統電壓外環-電流內環方式響應速度較慢，且不適應SEIGs的非線性特征；文獻[6]在電壓電流雙閉環控制的基礎上加入負載電流前饋環節，提高控制器的動態響應速度，但該模型僅在穩定工作點附近成立，抗干擾能力弱。文獻[7]介紹的滑模控制是一種切換控制，受控目標圍繞滑模面運動，與原系統模型沒有直接關系，具有較強的魯棒性，但低階滑模控制的抖振問題突出。文獻[8]采用反演控制將非線性系統分解為多個低階子系統，對每個子系統設計虛擬控制量以及李雅普諾夫函數，反向遞推至整個非線性系統。文獻[9]提出了一種適用于DC/DC變換器的神經網絡智能控制方法，調節能力較強。在實際非線性控制器的設計中，往往將多種非線性控制理論以及設計方法交叉使用，使控制器具備更優的控制性能。

強扭曲滑模控制是一種二階滑模控制[10]，可以實現滑模變量及其導數的有限時間收斂，能夠有效抑制低階滑模控制中的抖振現象[11-14]，具有魯棒性強、響應速度快等突出特點。本文以混合儲能系統為研究對象，在模型不確定上界未知條件下，提出一種分散自適應強扭曲虛擬阻抗控制新方法。為驗證所提方法的有效性，開展了物理參數攝動和連續負載沖擊的仿真實驗，與虛擬阻抗比例控制方法相比，所提新控制方法能夠實現高、低頻負載功率快速分配，可明顯縮短混合儲能系統輸出電壓的穩定時間，降低電壓超調，對提高HESS運行性能具有一定能力。

1 混合儲能系統非線性模型分析

由鋰電池組（CA）和超級電容（SC）構成的混合儲能系統拓撲結構如圖1所示。

圖1 HESS拓撲結構圖

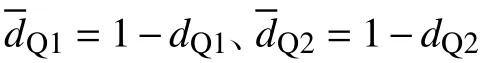
考慮濾波電感、濾波電容存在的物理參數分散性，儲能變換器非線性不確定模型可表示為：

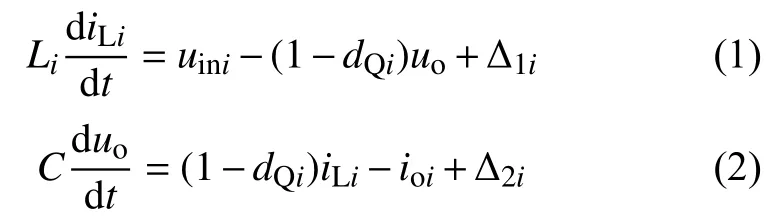
由式(1)、式(2)得：

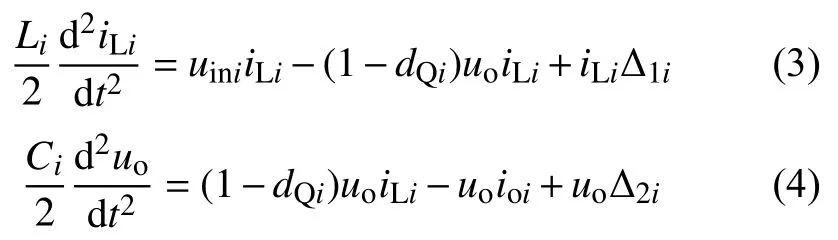
由式(3)、式(4)得：

由式(1)、式(5)得：

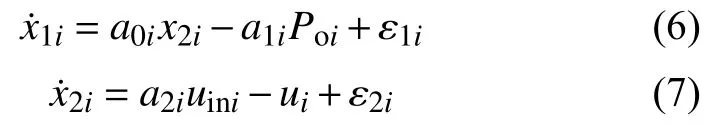
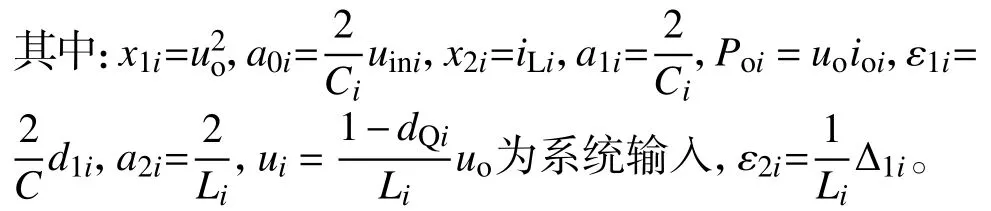
儲能變換器非線性模型式(6)、式(7)，w1i、w2i為 ε1i、ε2i的未知上界，且滿足 |ε1i|＜ w1i,|ε2i|＜ w2i。

2 混合儲能系統分散控制實現

2.1 分散自適應強扭曲控制算法

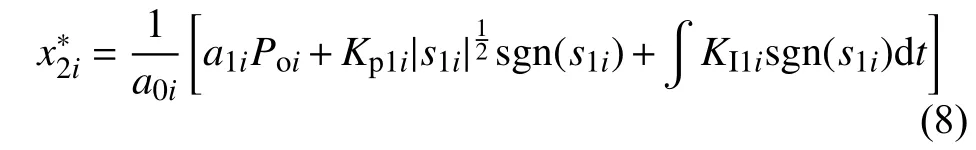
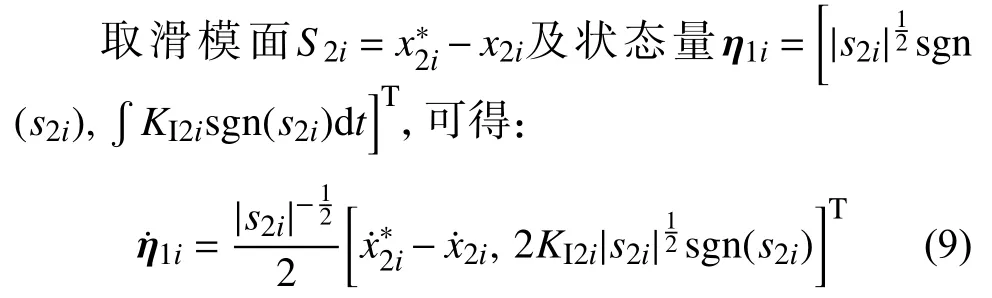
將式(8)代入式(9)得：

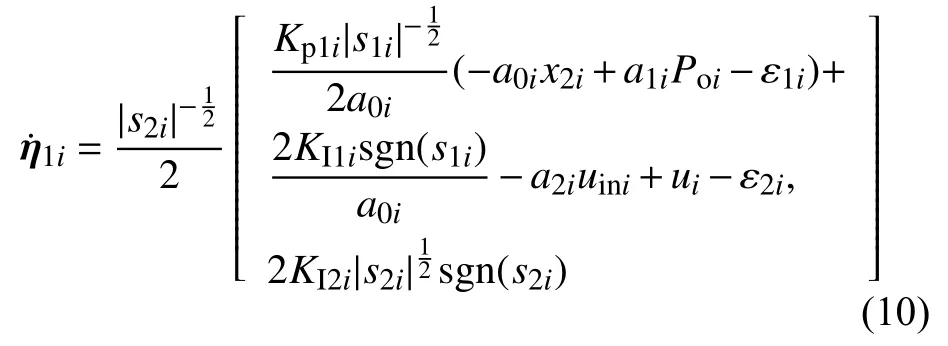
取控制律為：

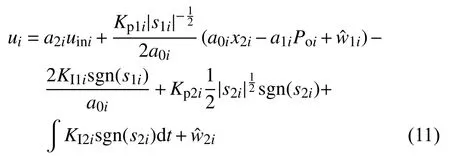
將式(11)代入(10)得：

取Lyapunov函數：

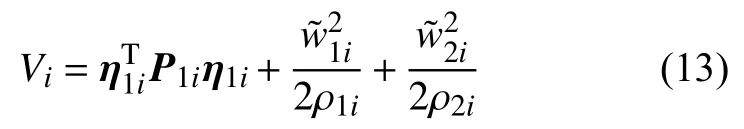
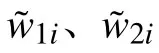
由式(13)得：

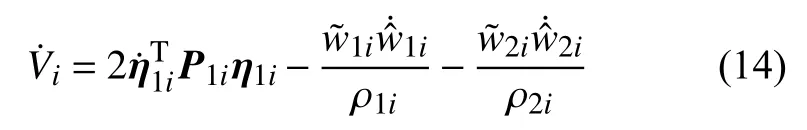
將式(12)代入(14)得：

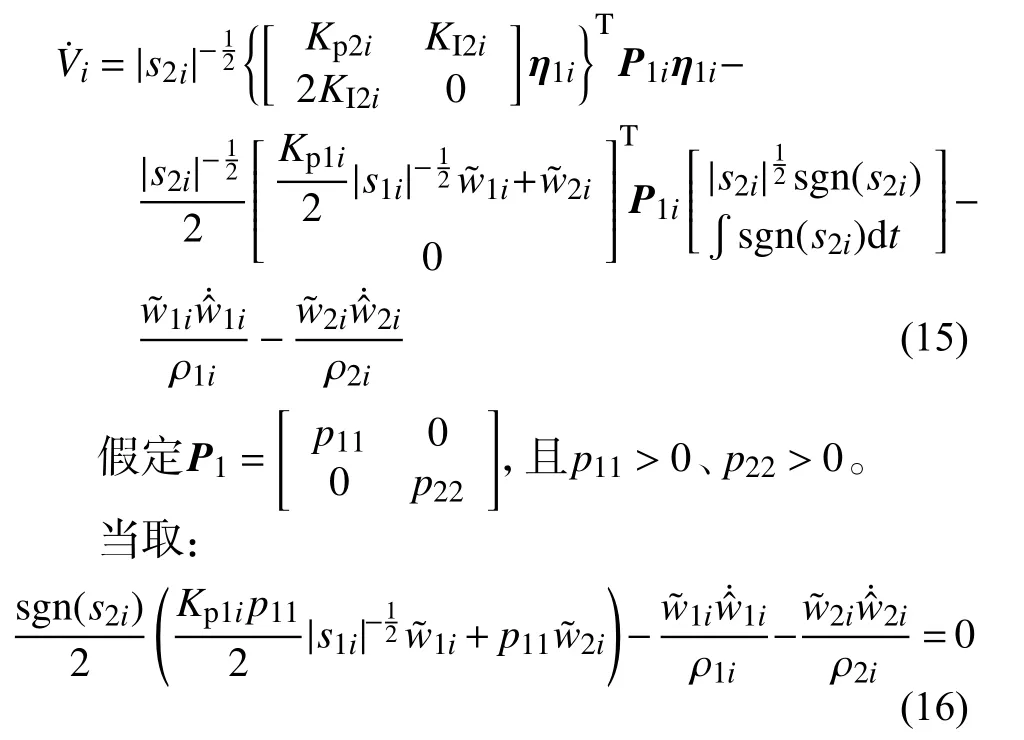
由式(16)得不確定上界自適應律為：

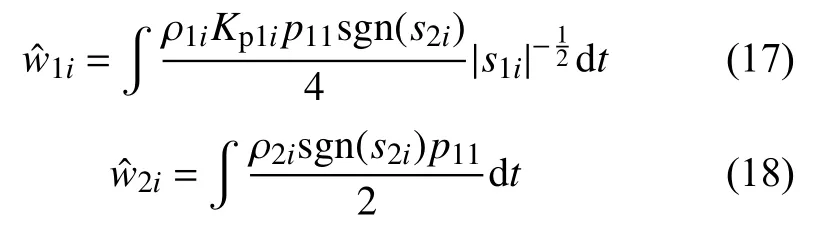
2.2 混合儲能系統穩定性分析

取混合儲能子系統Lyapunov函數為式(13)，當控制律為式(11)，不確定上界自適應律為式(17)、式 (18)，由式 (8)～式 (18)得：

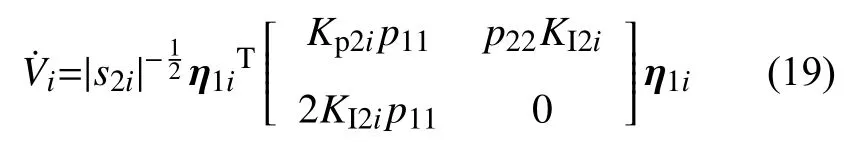
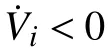
2.3 混合儲能系統虛擬阻抗控制原理框圖

HESS中蓄電池組用于分擔負載平穩功率，超級電容組用于分擔負載高頻功率，為有效實現功率的高低頻功率有效分配，提出采用虛擬阻抗控制策略。蓄電池組和超級電容組的控制原理框圖如圖2、圖3所示。

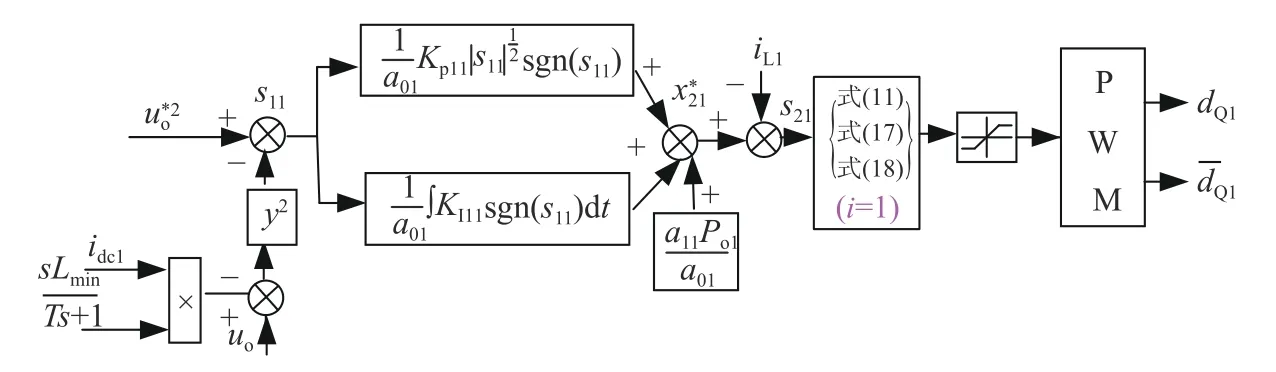
圖2 蓄電池組虛擬電抗強扭曲控制

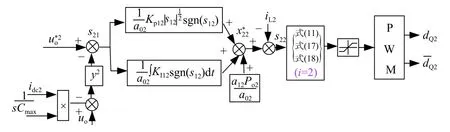
圖3 超級電容組虛擬電容強扭曲控制

蓄電池組與超級電容組均采用自適應強扭曲分散控制策略，二者的主要區別在于，蓄電池組電壓外環采用了虛擬電抗下垂控制方式，超級電容組電壓外環采用了虛擬電容下垂控制方式。采用虛擬下垂控制可以有效實現高低頻負載功率的分配。

3 仿真實驗與結果分析

為與傳統虛擬阻抗比例控制方式進行對比，驗證分散自適應強扭曲虛擬阻抗控制效果，在物理參數攝動和連續負載沖擊條件下，開展了仿真實驗。兩種控制方法都采用了虛擬阻抗控制方式，其中Lvirtual=100 mH，Cvirtual=100 μF。

鋰電池組參數：初始電壓200 V，額定容量50 Ah，初始SOC為100%，最大端電壓232 V，最大放電電流 20 A，內阻 0.04 Ω。

超級電容組參數：額定電容值100 F，內阻8.9 mΩ，初始電壓180 V。

儲能變換器參數：L1=2 mH，L2=4 mH，C1=1 200 μF，C2=1 500 μF。

鋰電池組儲能變換器采用傳統電壓外環-電流內環方式時，電壓外環控制參數為Kp=1、KI=2，電流內環控制參數為Kp=1.5、KI=3。超級電容組儲能變換器采用傳統比例控制方式時，電壓外環控制參數為Kp=1.5、KI=2.5，電流內環控制參數為Kp=3、KI=6。

鋰電池組儲能變換器采用自適應強扭曲分散控制參數時，控制參數為：Kp11=30，KI11=500，Kp12=70，KI12=1 000，ρ11=ρ21=1。超級電容組儲能變換器采用自適應強扭曲分散控制參數時，控制參數為：Kp21=20，KI21=300，Kp22=10，KI22=700，ρ12=ρ22=1。

3.1 物理參數攝動控制分析

在2.6 s時突加8 kW負載。分別采用傳統的電壓外環-電流內環虛擬阻抗控制方法和分散自適應強扭曲虛擬阻抗控制方法，仿真結果如圖4和圖5所示。

通過對比分析傳統虛擬阻抗比例控制方法（圖4）與分散自適應強扭曲虛擬阻抗控制方法（圖5）可以發現，在抗負載擾動和穩定時間方面，二者差別如表1、表2所示。

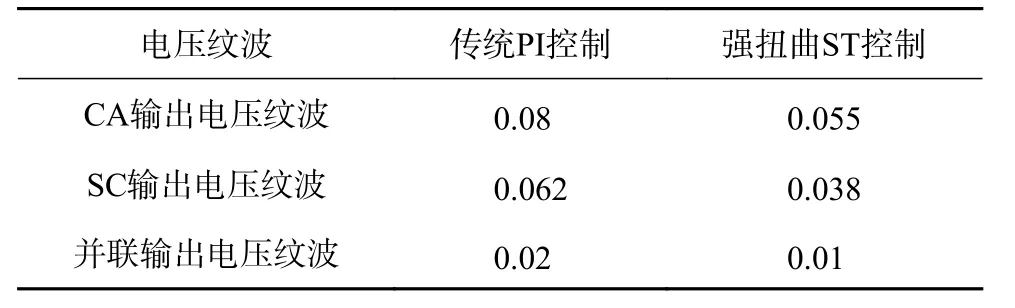
表1 抗負載擾動能力對比 %

表2 穩定時間對比 s

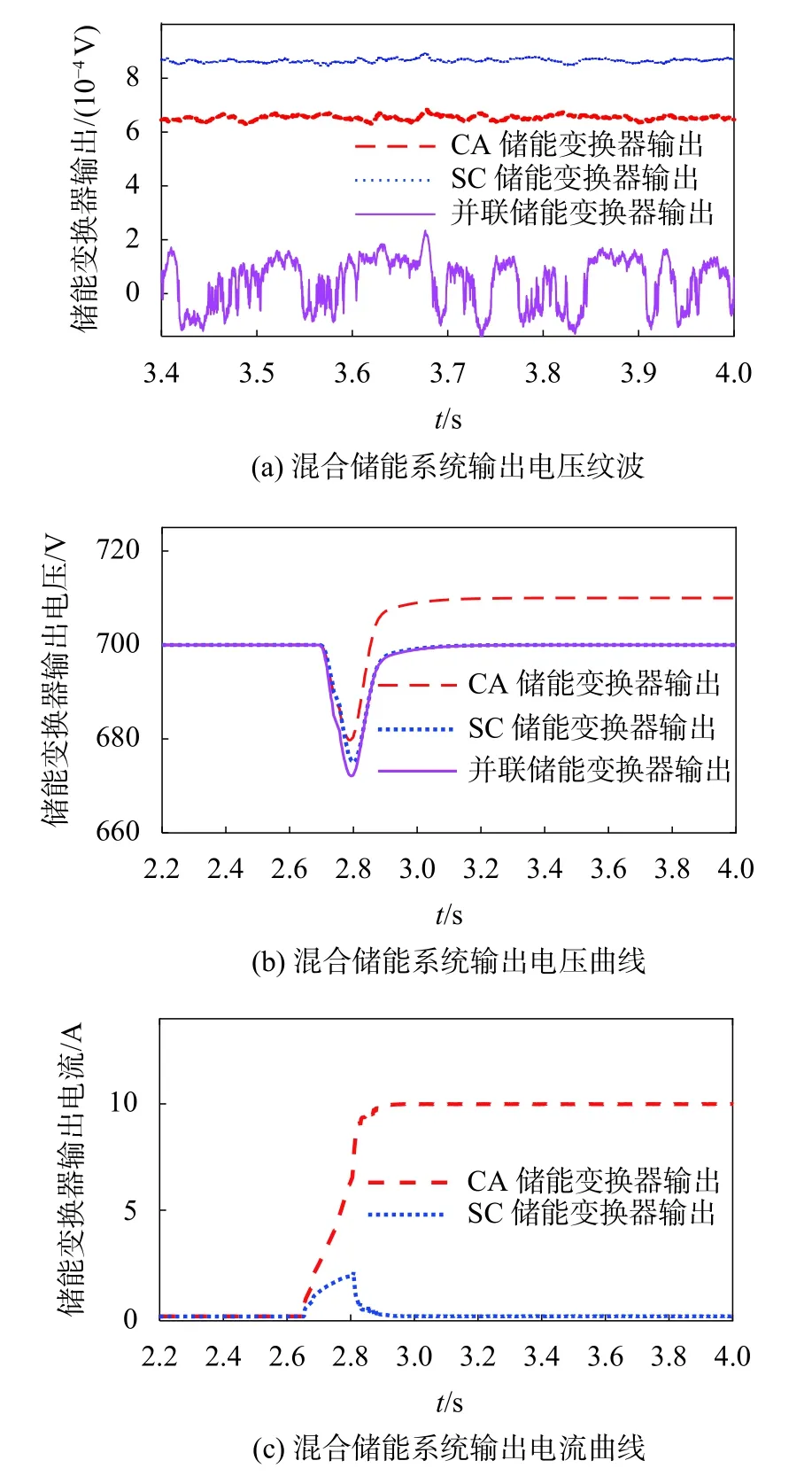
圖4 負載突增時，傳統虛擬阻抗比例控制仿真曲線

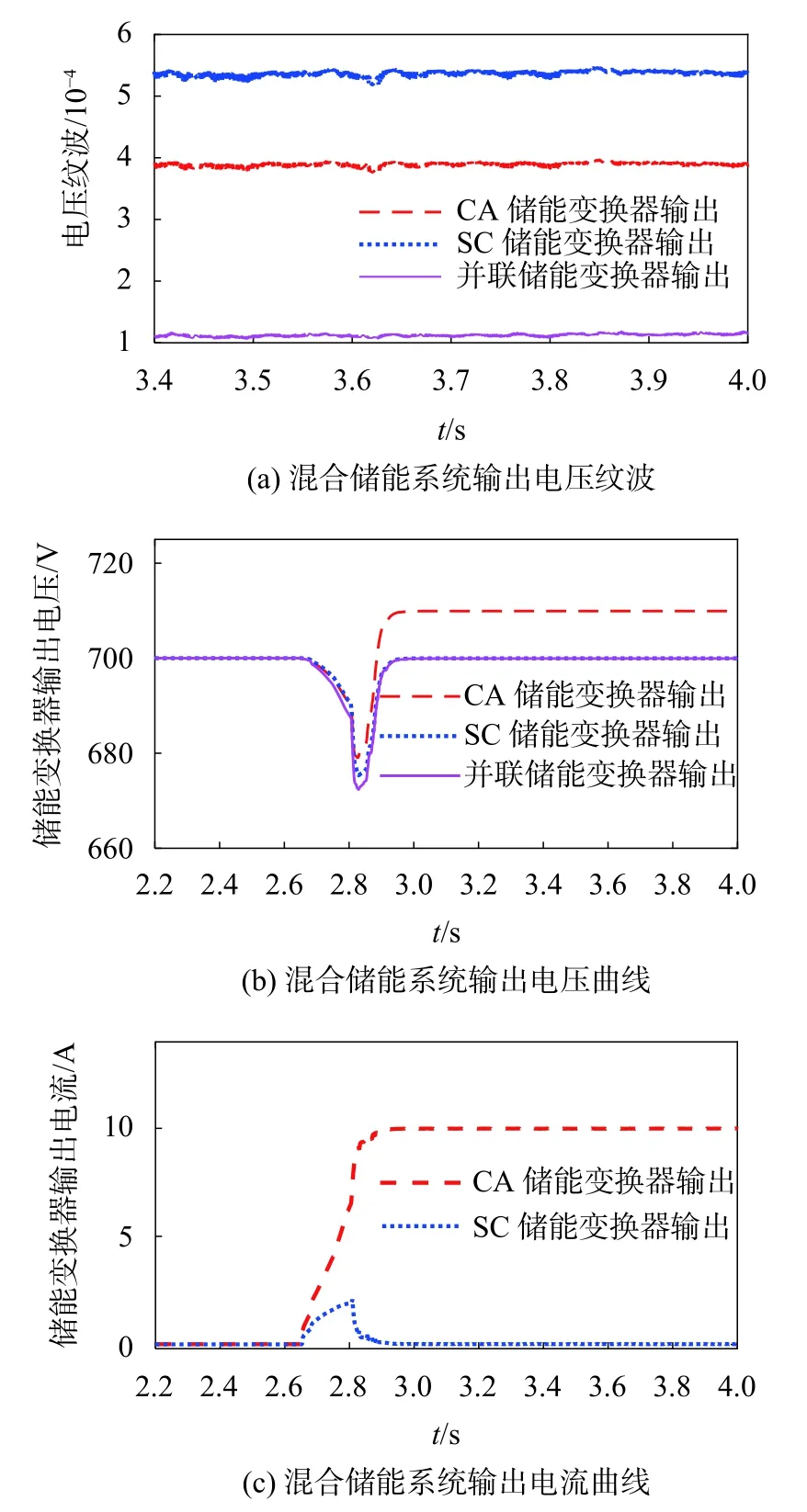
圖5 負載突增時，分散自適應強扭曲虛擬阻抗控制仿真曲線

由此可見，在負載突變條件下，分散自適應強扭曲虛擬控制算法具有更快的系統穩定控制速度。

3.2 連續負載沖擊實驗

負載功率為7 kW，負載沖擊頻率為66.7 Hz，采用傳統虛擬阻抗比例控制方式，仿真結果如圖6所示，當采用本文所提分散自適應強扭曲虛擬阻抗控制時，仿真結果如圖7所示。

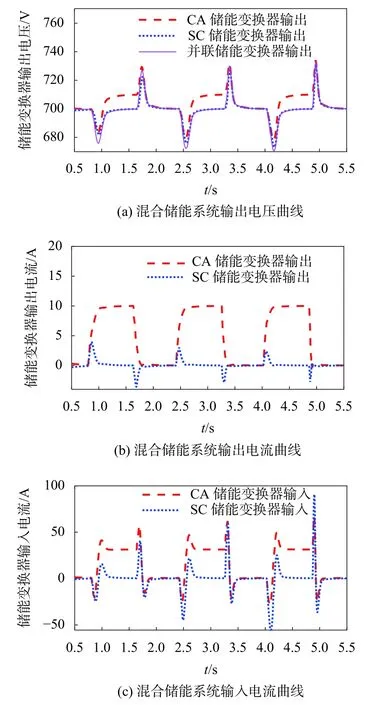
圖6 連續負載沖擊時，傳統虛擬阻抗比例控制仿真曲線

由圖6(a)和圖7(a)可知，電壓穩定時間由0.5 s縮短至0.2 s，電壓超調由730 V降低至720 V，由于采用虛擬電抗、電容控制，在負載突變時，超級電容可以對輸出功率進行快速補充，蓄電池組及超級電容組所用儲能變換器輸出電壓出現高于額定電壓的現象，原因是仿真過程中考慮了儲能變換器并聯時的輸電線路阻抗，并在輸電線路阻抗上產生了相應的壓降。由圖6(b)和圖7(b)可知，輸出電流穩定時間縮短一半，且超級電容輸出電流速度加快。由圖6(c)和圖7(c)可知，儲能變換器輸入電流響應時間由0.5 s縮短至0.2 s，且混合儲能系統能夠有效實現高、低頻功率的有效分配。抗沖擊負載能力對比如表3所示。

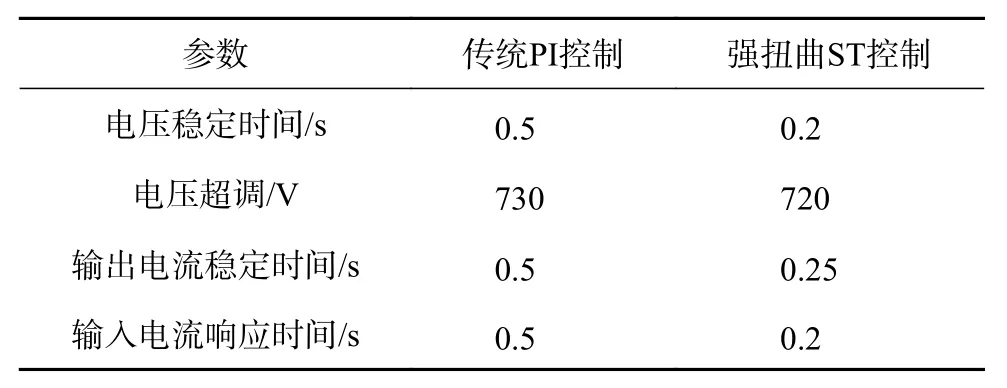
表3 抗沖擊負載能力對比

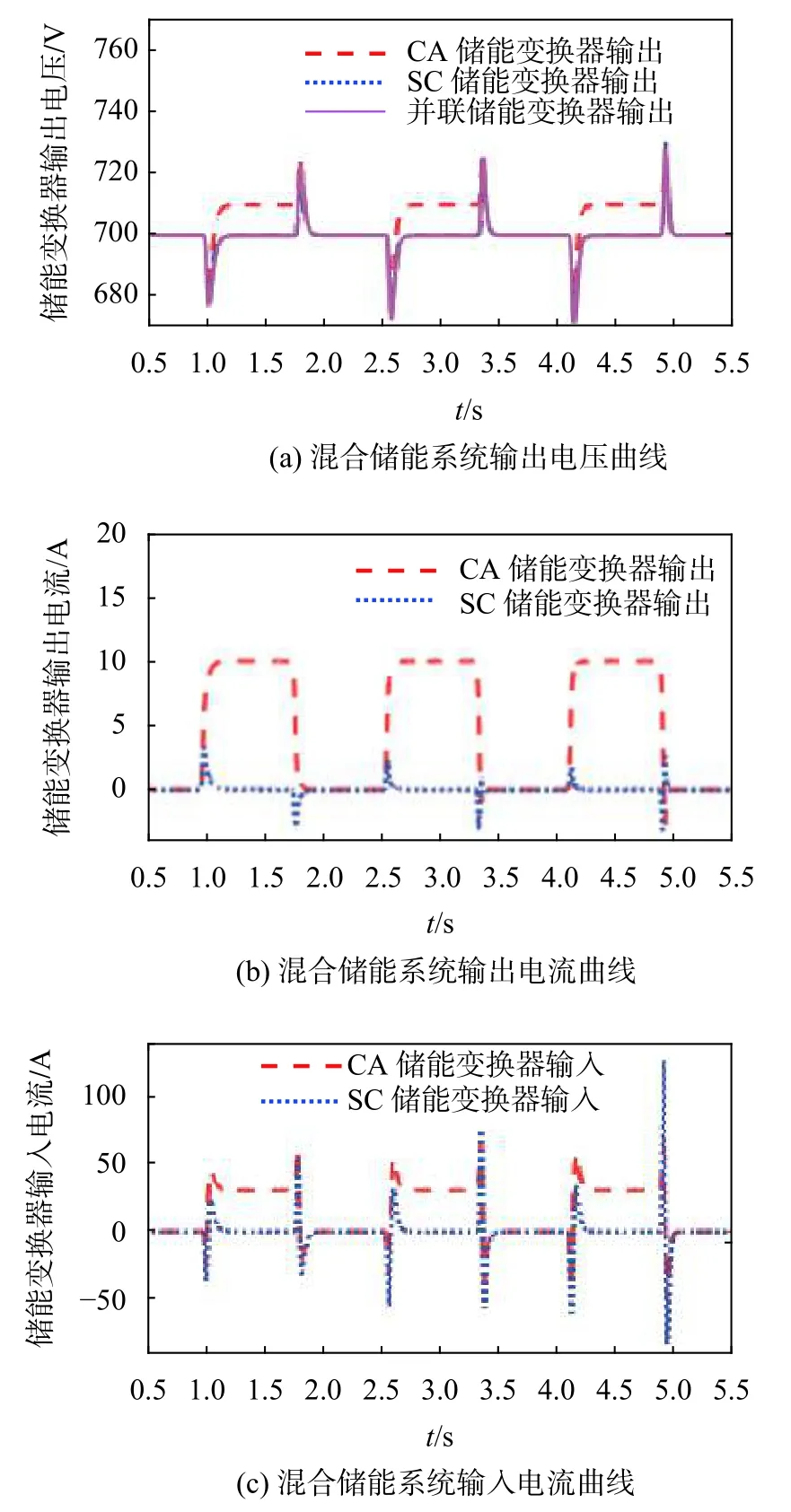
圖7 連續負載沖擊時，分散自適應強扭曲虛擬阻抗控制仿真曲線

由此可見，相比于傳統虛擬阻抗比例控制方式，分散自適應強扭曲虛擬阻抗控制具有更強抗沖擊負載能力。

4 結束語

為提高混合儲能系統（HESS）的抗負載沖擊能力，充分考慮物理模型存在的參數不確定及上界未知現實，本文提出一種新的適應強扭曲分散虛擬阻抗控制方法，并詳細闡述了強扭曲分散控制及虛擬阻抗控制的實現方法。為驗證所提算法的控制性能，比較與傳統虛擬阻抗比例控制方式的差別，開展了物理仿真測試對比實驗。仿真實驗結果表明，在物理參數攝動及連續負載沖擊條件下，新的控制方法能夠降低儲能變換器輸出電壓超調，縮短電壓穩定時間，超級電容組具有更快的瞬時功率響應速度，混合儲能系統能夠更快恢復穩定。因此，本文研究成果對提高高、低頻負載功率分配控制能力和HESS穩定運行能力具有一定能力。