基于改進KNN回歸算法的風電機組齒輪箱狀態監測

劉長良，張書瑤，王梓齊

(1.華北電力大學 新能源電力系統國家重點實驗室，北京 102206;2.華北電力大學控制與計算機工程學院，河北 保定 071000)

0 引 言

齒輪箱是風電機組的重要機械部件且常年處于運轉狀態，極易發生故障造成機組停機，給生產帶來經濟損失。據文獻統計[1-2]，由齒輪箱引起的故障停機時間顯著高于其他部件，因此有必要對齒輪箱進行狀態監測。目前齒輪箱狀態監測方法研究可分為離線監測和在線監測兩種。離線監測主要有油液成分監測[3]和振動監測[4]。在線監測是利用監控與數據采集（supervisory control and data acquisition，SCADA）系統[5]在線采集風電機組運行數據并對齒輪箱進行在線狀態監測，因不需額外加裝傳感器且實時高效，已成為齒輪箱狀態監測的研究重點。

基于正常行為建模的狀態監測方法是一種目前受到廣泛關注的建模方式，其基本思想是根據正常運行狀態下的歷史數據，對實時值進行估計，步驟主要分為數據處理、狀態變量建模和殘差分析3部分。根據是否顯式包含可估參數，通常可以分為參數建模和非參數建模方法兩種。參數建模方法主要有BP神經網絡[6-7]、分段支持向量機[8]、深度學習網絡[9]等；非參數建模方法主要有K近鄰（K-nearest neighbor，KNN）回歸算法[10-11]、非線性狀態估計（nonlinear state estimate technology，NSET）方法[12]、核密度估計[13]等。參數建模方法具有易于理解且訓練速度快的優點，但依托訓練樣本且模型后期維護困難，不適于風電機組復雜的運行狀況。KNN回歸算法是一種常用的非參數回歸方法，具有思路簡單、應用靈活、對異常值不敏感的優點，且不需要像神經網絡等前期進行參數或結構的學習和尋優。但KNN回歸算法仍需要一定的訓練數據，在訓練集過于龐大時，會嚴重影響運算效率。

訓練集中常存在離群點和相似點。離群點雖然不會對預測精度產生較大影響，但KNN回歸算法距離度量過程需要遍歷訓練集中每一個訓練樣本，所以離群點的存在會使運算時間延長。文獻[11]提出了一種剪輯算法，剔除了訓練集中與樣本整體偏離較大的離群點，實現了工業應用中運算效率的提高。相似點中包含大量的相似信息，不僅會占用計算資源，且會使選出用于計算預測值的近鄰樣本不能達到全面覆蓋真實運行狀況的期望，適度的剔除可以提升運算效率。文獻[14]根據樣本相似度剔除了訓練集中相似點來縮小訓練集，在運算精度和運算效率方面均有提升。

本文針對風電機組狀態監測問題，提出了改進距離度量公式的KNN回歸算法，并同時剪輯離群點和相似點對訓練集進行優化以提升運算效率。以某2 MW風電機組SCADA系統采集數據為例，對風電機組發生故障停機和維修投運后的2組全工況歷史數據分別進行實驗。對對照組進行實驗確定剪輯離群點和相似點的閾值，以實驗組基準集的殘差為依據，利用SPC技術結合滑動窗口法得到異常率曲線，實現風電機組齒輪箱的狀態監測。

1 KNN回歸算法及訓練集優化

1.1 經典KNN回歸算法

KNN回歸算法是一種基于實例的學習方法，其核心思想是建立向量空間模型，基于某種距離度量方式，找到訓練集中與測試點最接近的 k個近鄰點，利用這 k個近鄰點對測試集進行預測，在回歸問題中常采用平均法，即這 k個近鄰點輸出的平均值作為預測結果，其步驟如下：

2）遍歷訓練集中各點 Xi，求其與測試集中某點的歐氏距離 L：

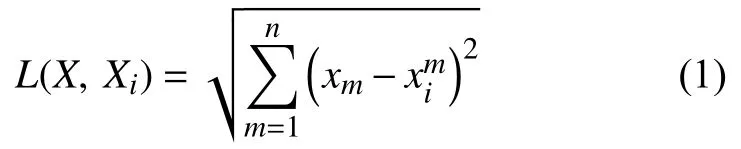
3）對求得的距離大小進行排序，選擇訓練集中與 X 最近的 k 個近鄰點 Xj(1≤j≤k)，這 k個近鄰點輸出的平均值作為 X的輸出預測值，即：

經典KNN回歸算法中認為測試集實際輸出未知，所以在距離計算時不考慮輸出值，但在風電機組齒輪箱狀態監測問題中，測試集實際輸出 y可以由SCADA系統測得，所以本文針對狀態監測問題特點提出對經典KNN回歸算法距離度量公式的改進。

1.2 面向狀態監測問題的KNN回歸算法

經典KNN回歸算法的本質是根據輸入值 X 定量預測得到預測輸出值，即，此時輸出值y未知；狀態監測問題關注當前研究對象是否偏離正常狀態，所以選定一個狀態特征作為對研究對象運行狀態的反映，如本文所選齒輪箱軸承溫度，并建立齒輪箱正常運行情況下的模型，在實際生產中，各個狀態特征與當前運行狀態都存在關聯，其實時值可以在線采集，所以狀態監測問題的實質是：已知當前實時運行狀態和正常行為模型，求得模型輸出，并與正常運行狀態求偏差，若偏差超過設定閾值，則認為此時研究對象已處在異常狀態。其中 X 為其他狀態特征（如風速、環境溫度等），y為齒輪箱軸承實時溫度，為計算得到的齒輪箱軸承溫度。本文針對這一特點，改進經典KNN回歸算法距離度量公式，使測試集實際輸出與輸入向量地位等價參與距離計算，改進后距離度量公式如下：

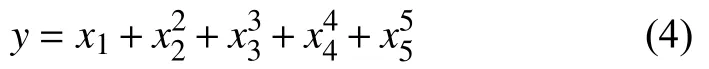
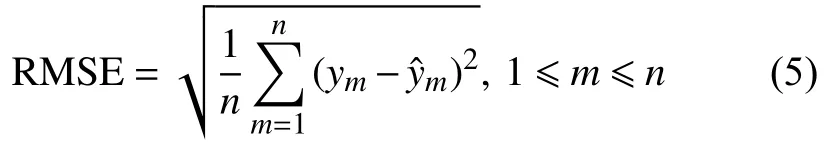
由表1可知，改進KNN回歸算法預測精度較未改進提升59.6%，在運算效率基本不變的情況下，預測精度有大幅度提升。

表1 改進KNN回歸算法測試

1.3 KNN回歸算法訓練集優化

KNN回歸算法是數據驅動的一種惰性算法，所以運算效率和預測精度很大程度取決于訓練集的選取，但由于實際工況復雜，訓練集中常存在離群點和相似點對預測過程造成影響，所以在本文提出同時剪輯訓練集中離群點和相似點的思路，應用提出的兩種剪輯算法分別對離群點和相似點予以剔除以優化訓練集。

由于實際運行現場不可避免地存在噪聲等因素，且SCADA系統采集數據具有隨機性，數據中常存在遠離訓練集中大部分點的點，即離群點。離群點不能反映風電機組齒輪箱正常工作狀態，有可能是存在故障的點。從預測角度來說，當選取 k值較小時，離群點不會影響預測精度，當選擇 k值較大時，會造成預測精度降低；從運算效率角度來看，KNN回歸算法距離度量會遍歷訓練集全體，所以離群點存在會使運算效率降低，增加存儲成本，因此提出一種改進文獻[11]的剪輯離群點流程的訓練集優化方法，具體步驟如下：

2）對訓練集中每一個點遍歷步驟1），得到對應的預測值。

3）求得預測值與實際輸出值的相對誤差絕對值Qi

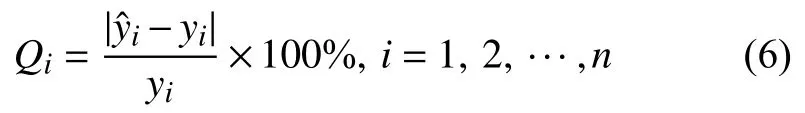
式中：yi——實際輸出值；

相似點是指訓練集中距離較小的點，其過多會使訓練集中儲存大量重復冗余的信息。從預測精度角度考慮，當選擇的 k個近鄰點中存在大量相似點而無法覆蓋風電機組齒輪箱真實運行狀況時會使預測精度下降；從運算效率考慮，相似點會占用計算空間，使運算效率下降，所以在此提出一種改進文獻[14]中相似度函數的剪輯相似點算法，具體步驟如下：

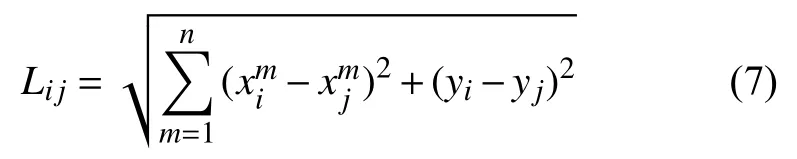
其中，Lij表示Xi與Xj之間的距離度量。

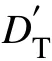
2 基于SCADA數據的風電機組齒輪箱狀態監測

正常行為建模（normal behavior modeling，NBM）應用于狀態監測的基本思想是：根據正常狀態下的歷史數據建立有關預測量的模型并得到預測輸出值，通過模型預測輸出與實際輸出值的殘差判斷齒輪箱是否偏離正常運行狀態。本文采用結合訓練集優化的改進KNN回歸算法對風電機組齒輪箱進行狀態監測，其具體流程如圖1所示。

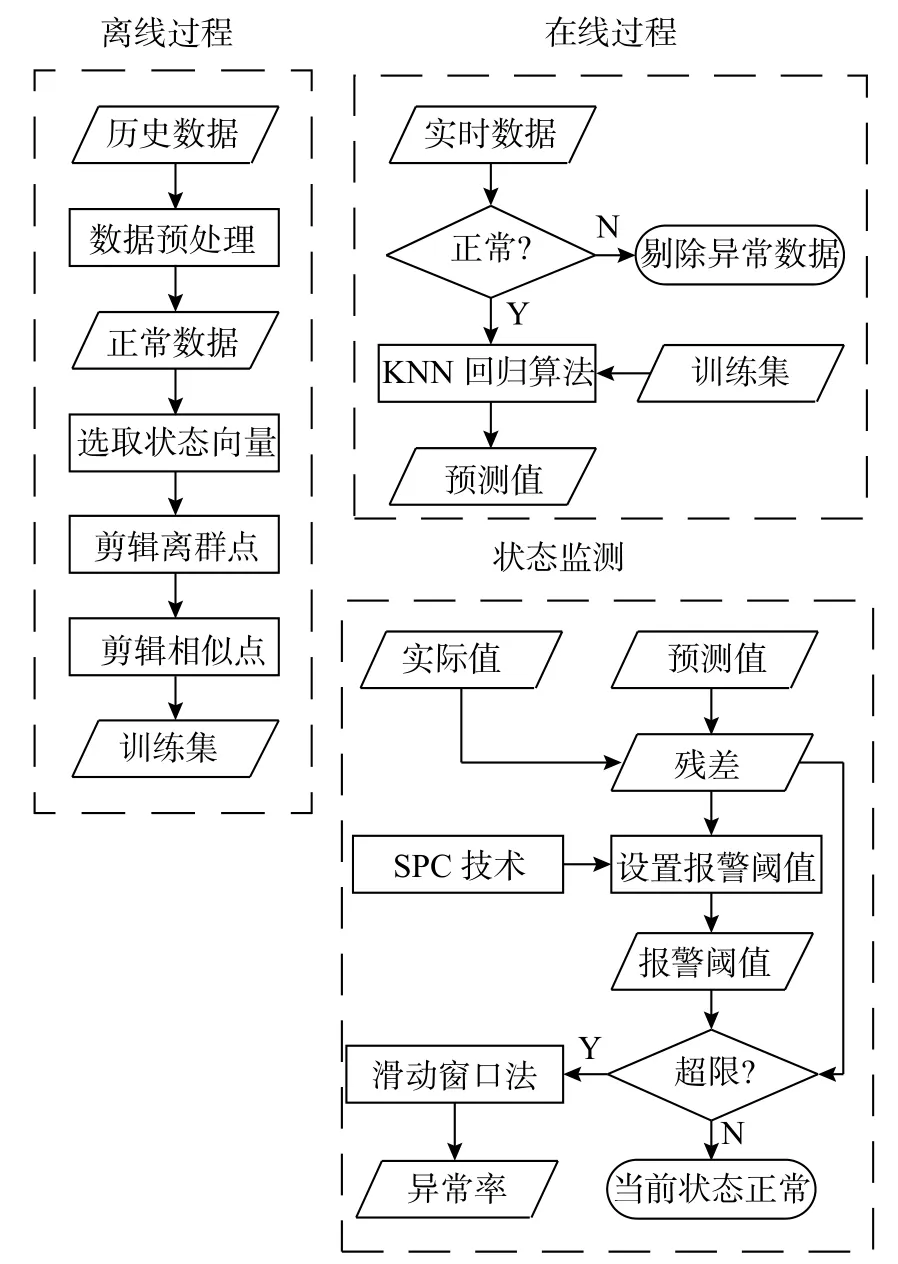
圖1 改進KNN回歸算法流程圖

1）離線過程：采集正常運行狀況的SCADA系統歷史數據并進行預處理，包括剔除缺失和異常數據、選取狀態向量，結合1.3訓練集優化方法對原始訓練集進行離群點和相似點剪輯得到新訓練集。

2）在線過程：采集SCADA系統實時數據，利用改進KNN回歸算法得到預測輸出值。

3 風電機組齒輪箱數據預處理及訓練集優化算法

3.1 研究對象

本文的研究對象為福建省某風場的一臺2 MW雙饋式風電機組，型號為Vestas公司的V90-2.0 MW。機組的切入風速為4 m/s，切出風速為25 m/s，齒輪箱結構為二級螺旋齒輪和一級行星齒輪，SCADA系統的采樣周期為10 min。該機組于2016年7月13日10:20發生齒輪箱故障導致停運，經維修后于7月18日9:30恢復正常重新投運。

從 SCADA數據庫中導出2016年1月 1日0:00-7月13日10:20齒輪箱故障前的運行數據和7月18日9:30-12月31日23:50齒輪箱維修后的運行數據，分別稱為實驗組（故障前）和對照組（維修后）。數據中可用的運行參數有8個，分別為風速、發電機轉速、葉輪轉速、風向角、環境溫度、無功功率、有功功率、齒輪箱軸承溫度。

3.2 數據預處理

齒輪箱軸承是齒輪箱主軸的載體，在選取的參數中，齒輪箱軸承溫度能夠直觀迅速地反映齒輪箱整體運行狀況，故選作預測向量。剔除數據缺失、有功功率不大于零、風速小于切入風速或大于切出風速的數據點，并基于拉依達準則去除異常數據后，實驗組和對照組分別用14 000組數據進行實驗。

經過計算各項和齒輪箱軸承溫度的皮爾遜相關系數得到，風速、發電機轉速、葉輪轉速、有功功率4項與齒輪箱軸承溫度存在著正相關關系，可以作為狀態向量；環境溫度雖然與齒輪箱軸承溫度相關性不大，但是由于環境溫度的變化對齒輪箱工作環境影響較大，所以把環境溫度也作為一個狀態向量考慮；由于葉輪轉速和發電機轉速存在顯著的相關性，所以本文選用風速、發電機轉速、環境溫度、有功功率作為狀態向量并對其進行歸一化以避免量綱影響。運行參數變化范圍及皮爾遜相關系數見表2。

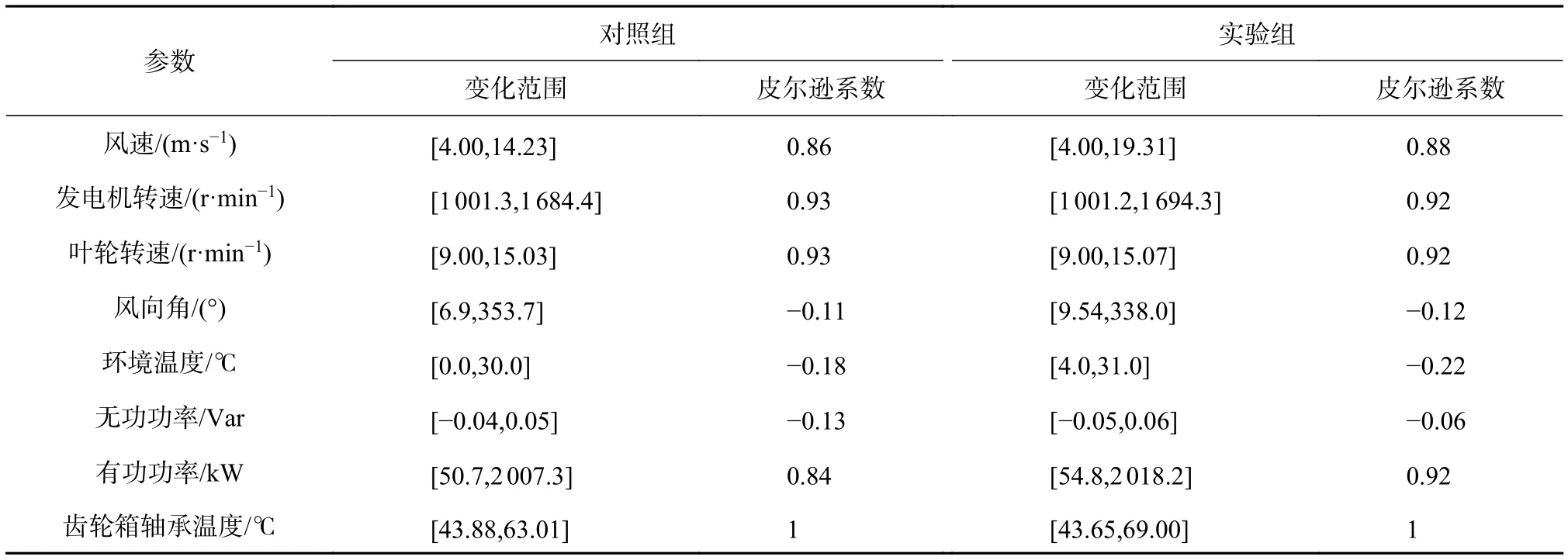
表2 運行參數變化范圍及皮爾遜相關系數

實驗組和對照組分別以各自數據的第1～7 000號樣本作為訓練集，第7 001～14 000號數據為測試集，其中第7 001～7 500號作為預測精度基準。本實驗基于 Matlab 2019（運行于 Intel i7-10710U CPU,16.0 GB RAM的PC機）進行。對對照組測試集分別應用經典和改進KNN回歸算法，其中經典KNN回歸算法RMSE為0.040 7，改進后RMSE為0.016 2，較未改進提升60.20%，仿真結果表明改進距離度量公式使預測精度顯著提升。

3.3 離群點剪輯

本文對對照組訓練集進行離群點剪輯，以對照組基準集的RMSE和測試集運算效率作為根據，確定剪輯閾值θ1并對測試集進行預測，圖2和表3為新訓練集 DT的樣本個數、基準集RMSE及運算時間。

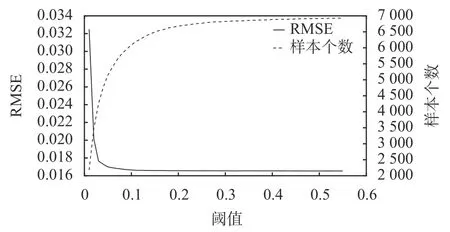
圖2 剪輯離群點訓練集樣本個數、均方根誤差

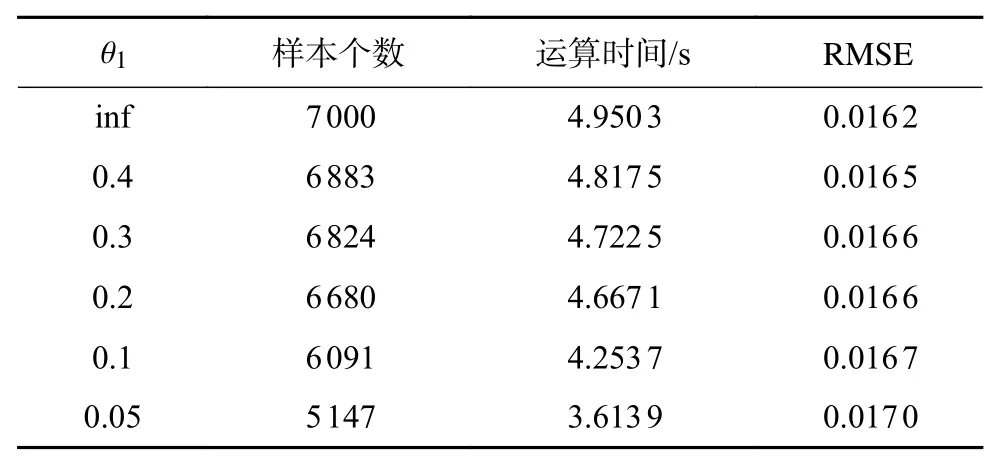
表3 剪輯離群點訓練集剩余樣本個數、均方根誤差及運算時間1）

由圖表可以得到以下結論：

1）從運算效率來看，隨著閾值θ1的減小，訓練集樣本個數減少，運算效率隨之上升；當θ1≥0.2，訓練集樣本個數下降緩慢，在 0.1≤θ1≤0.2時，訓練集樣本個數減少速度上升，之后仍在快速下降，說明離群點大部分處于θ1≥0.2的部分，當θ1≤0.1時，訓練集中剩余樣本點分布密集，可以認為是有效數據。

2）從預測精度來看，當θ1≤0.05時，RMSE迅速上升，說明此時訓練集損失一部分有效訓練樣本，使預測精度下降。

綜合以上分析，選擇θ1=0.1，此時預測精度下降3.0%，運算效率提升14.07%，訓練集 DT剩余樣本數為6 091。

3.4 相似點剪輯

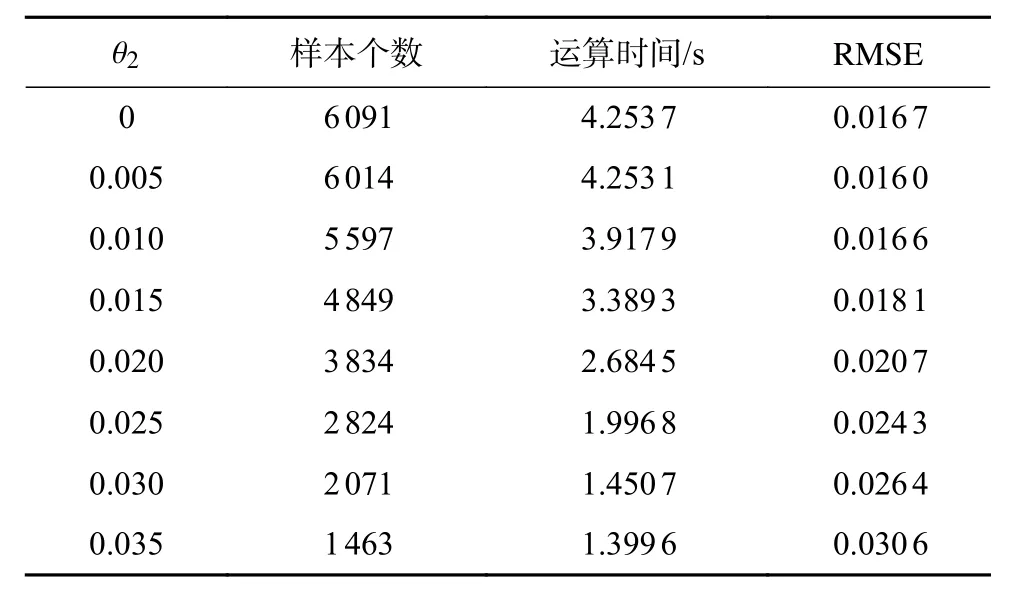
表4 剪輯相似點訓練集剩余樣本個數、均方根誤差及運算時間

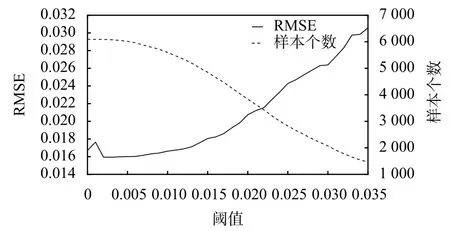
圖3 剪輯相似點訓練集樣本個數、均方根誤差

分析圖表可得以下結論：

1）從RMSE來看，其整體趨勢呈現一直上升的狀態，即預測精度下降，當θ2=0.035時，相比于原始訓練集RMSE降低了88.89%，此時預測精度不符合工程要求和設計預期。

2）從剪輯后訓練集樣本個數來看，當θ2≤0.01時，訓練集樣本個數下降速度平緩，當θ2≥0.01時，訓練集樣本個數下降速度加快，可以認為此時已經基本剔除極端相似的點，當閾值繼續增大時，可能會過度剪輯造成預測精度下降。

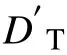
4 風電機組齒輪箱故障監測實例及結果分析

4.1 SPC技術

統計過程控制（statistical process control,SPC）技術[15-16]，主要是利用過程波動的統計規律性對過程進行分析控制。由于齒輪箱故障多表現為某部件溫度升高，所以在此只考慮報警上限。本文設定報警閾值的步驟如下：

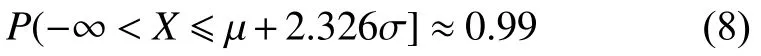
若 X的取值長期超出式（8）的區間，可以認為過程受到了異常因素的影響出現故障。因此，根據正態分布的均值 μ和方差 σ2可以設計預測殘差的預警閾值。

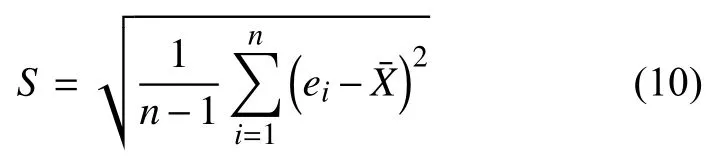
式中：ei——預測殘差；

n——測試集的樣本個數。

若齒輪箱軸承溫度長期高于閾值T，則認為此時齒輪箱已出現顯著故障。

4.2 風電機組齒輪箱狀態監測實例

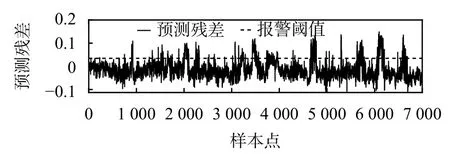
圖4 預測殘差與閾值

式中：N——當前滑動窗口中超出閾值的點個數；

M——滑動窗口長度。

本文取滑動窗口長度為1 000，則齒輪箱異常率如圖5所示。

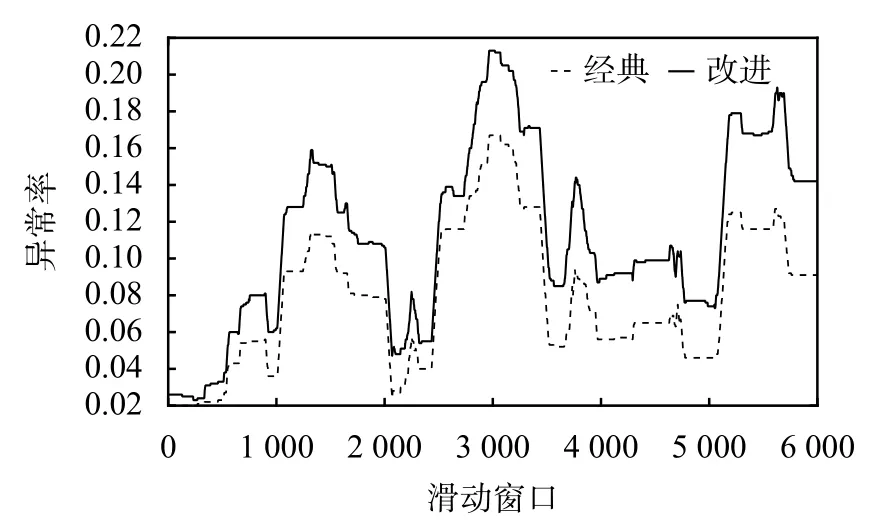
圖5 齒輪箱異常率

改進KNN回歸算法監測齒輪箱狀態得到的異常率曲線在第1～300個滑動窗口處較低且平穩，認為此時齒輪箱仍處于正常運行狀態，第300～1 000個滑動窗口處異常率出現逐漸上升現象，認為此時齒輪箱已處于前期故障中，第1 000號窗口后，齒輪箱異常率相較前1 000號窗口異常率迅速上升至較大值，此時異常率遠高于第1～300個滑動窗口，且多次出現起伏現象，認為此時齒輪箱已處于嚴重故障狀態。

經典KNN回歸算法報警閾值為0.080 8，高于改進后算法報警閾值，在故障預警中會表現出對齒輪箱軸承溫度變化不敏感，雖然異常率曲線與改進后趨勢相同，但故障預警能力較改進后弱，可能會延誤報警。

5 結束語

本文針對風電機組齒輪箱狀態監測提出了KNN回歸算法建立正常行為模型，并對經典KNN回歸算法距離度量提出了改進。應用剪輯算法優化訓練集，實現了風電機組齒輪箱的狀態監測，得到以下結論：

1）結合狀態監測問題特點，對經典KNN回歸算法進行距離度量公式的改進，大幅度提高了KNN回歸算法的預測精度。

2）對訓練集剪輯離群點和相似點進行優化，可以在工程允許的精度損失范圍內，壓縮訓練集樣本個數，提升運算效率。

3）結合訓練集優化的改進KNN回歸算法能夠實現風電機組齒輪箱故障的提前預警，且滑動窗口法監測齒輪箱異常率比殘差報警方式更直觀、清晰，且誤報警率低，更適用于工業生產中。