恒星觀測與新天文學革命

王廣超 鄭涵

摘 要 近代歐洲的新天文學革命主要得益于古希臘時期即已成熟的偕日升觀測技術以及黃道十二宮為主的坐標體系。古希臘天文學家對歲差現象有深刻的認識，使得后來的第谷能夠創建一套更為精密的恒星表，為開普勒發現橢圓定律奠定基礎。而古代中國的恒星觀測采用了沖日法和以二十八宿為主的坐標體系，由于缺乏對歲差效應的準確的理解和解釋，中國古代天文學理論在根本上是不確定的。

關鍵詞 恒星觀測 托勒密 第谷 開普勒 天文學革命

中圖分類號 N09∶P1

文獻標識碼 A

收稿日期：2021-08-06

作者簡介：王廣超，1975年生，北京人，理學博士，中國科學院大學人文學院科學技術史系教授，研究方向為天文學史;鄭涵，1998年生，廣東潮州人，中國科學院大學人文學院科學技術史系碩士研究生，研究方向為天文學史。

基金項目：國家自然科學基金面上項目（項目編號：11973043）;中央高校基本科研業務費專項資金。

① 康德在《純粹理性批判》第2版序言中指出：“這里的情況與哥白尼最初的思想是相同的。哥白尼在假定整個星群都圍繞觀察者旋轉，對天體運動的解釋就無法順利進行之后，試一試讓觀察者旋轉而星體靜止，是否可以更為成功。”這被認為是康德自認為開辟了形而上學領域內的“哥白尼式革命”的文本依據。參見[1]。

提起科學革命，我們一般會想到哥白尼革命，正是哥白尼（N. Copernicus，1473—1543）提出日心地動說，改變了人們長久以來篤信的地心學說。18世紀的哲學家康德甚至把自己的認識論描述成了“哥白尼式革命”①。但是，近代天文學革命并非是哥白尼而是由開普勒（J.Kepler，1571—1630）實現的。因為，盡管哥白尼提出顛覆性的日心-地動學說，但他依然使用亞里士多德（公元前384—322）的概念如常規運動、天球等建構其體系，甚至可以說，哥白尼是“根據亞里士多德的原則否定了托勒密（C. Ptolemaeus，100—170）的宇宙模型”（[2]，頁62）。開普勒則不同，他提出了行星運動三定律，更重要的，由于行星的運動軌跡是橢圓而非正圓，開普勒建構出了一套全新物理學理論來解釋行星運動。開普勒何以能發現行星運動三定律？一般認為是基于第谷（Tycho Brahe，1546—1601）對火星運動的觀測，正如《新天文學》（New Astronomy）完整書名“根據因果關系、或根據尊貴的第谷對火星運動的觀測而導出的天界物理學所作的新天文學”Reasoned from Causes， or Celestial Physics， Treated by Means of Commentaries on the Motions of the Star Mars， from the Observations of the noble Tycho Brahe.表述的那樣。而實際上，一個更具決定性的因素是歐洲長久以來形成的恒星觀測技術。

本文嘗試從古代的歐洲與中國在恒星觀測技術方面上的不同入手，探討何以是西方而非中國發生新天文學革命，并追溯至古希臘時期確立的恒星觀測技術。第谷在古希臘恒星觀測的基礎上創建出一套精密的星表，是開普勒提出橢圓定律和面積定律的經驗基礎。然而，中國的恒星觀測技術并不支持產生像西方那樣的革命，主要是由于缺乏一個恒定不變的坐標體系，以及對歲差問題的透徹理解。

一 新天文學革命

哥白尼在天文學的主要貢獻是提出日心-地動模型。實際上，他對恒星位置的測算以及恒星表的編訂非常重視，甚至將“恒星表”至于首位，認為準確的恒星數據是研究行星運動的基礎。《天球運行論》（On the Revolutions of the Heavenly Spheres）中有一張完整的恒星表，主要基于《至大論》（Almagest）此書名有學者譯為《天文學大成》，是古希臘托勒密在約公元140年編纂的一部數學、天文學專著。中的星表改編而成[3]，將其中恒星的黃經值減去6度40分，而黃緯不變。在編制星表過程中，哥白尼曾利用“渾儀”（armillary sphere）對托勒密的數據進行復驗，發現有不少偏誤，但他只對其中的獅子座α（Regulus）和室女α（Spica）的數據做了些許調整[4]。

哥白尼認為《至大論》最主要的問題是未給予恒星表以足夠重視。在《至大論》中，恒星表被置于第7章的第5節到第8章的第1節之間，位于日月運動理論之后，潛在的理由是恒星的位置坐標是以一些在黃道上的具體恒星，如獅子座α（Regulus）、室女座α（Spica）（即距星）為根據的，這些距星的位置則依據太陽以及月亮的位置而算定。哥白尼將“計算恒星的位置，設置恒星星表”一節放在了《天球運行論》的第二部分，主要討論天球坐標系的各種圈：地平圈、黃道圈、赤道圈，以及黃赤交角和基本坐標系問題。很顯然，哥白尼試圖將恒星數據作為更基本的參照對象。從這一安排中哥白尼似乎已隱約預見到，將來天文學的真正突破將寄托于更精準地測定恒星位置[5]。

盡管哥白尼提出了顛覆性的日心地動學說，但他的理論是在傳統的古希臘宇宙論基礎上搭建起來的。他認為行星附著在天球上隨天球一起旋轉，天界的物體做常規勻速圓周運動。這些理論來自亞里士多德，而哥白尼試圖革新的其實是托勒密的理論，尤其是其中的偏心-等速點模型（equant）。在他看來，偏心等速點（equant point）既不是本輪的中心，也不在本輪上，卻是行星運動的參照點，而這一點本身沒有實際的物理意義，這在哥白尼看來不能令人滿意。正是由于認識到偏心等速點模型的缺陷，哥白尼試圖找到一種更為合理的模型[6]。

開普勒之所以提出行星運動三定律、發表《新天文學》，部分原因要歸于他獲得了第谷的觀測數據。《新天文學》出版于1609年，1600年開普勒受邀協助第谷做天文學研究。早在1596年，開普勒曾出版《神秘的宇宙》一書，試圖論證哥白尼的日心說是正確的，盡管此書有不少錯誤，卻充分地展現了其在數學方面的才能，而這正是他受到第谷青睞的主要原因。第谷希望開普勒根據他畢生心血積累起來的觀測數據建立“日心地不動”學說，即介于哥白尼和亞里士多德之間的調和模型：太陽為行星運動的中心，日月圍繞地球做勻速圓周運動。開普勒起初在構建模型時卻曾依照第谷體系，后來卻發現它與其觀測數據有較大的差誤，最終他不得不放棄之前的承諾。

基于第谷的觀測數據，開普勒于1602年完成面積定律的構建，期間，他主要使用第谷遺留的火星在沖點位置時的數據，計算火星軌道的參數。所謂“沖”，就是火星和太陽的經度正好相差180°，或者說火星、地球和太陽三者正好處于一條直線上，地球在中間，火星和太陽分處兩邊。1580—1600年，第谷留下10個這樣的觀測記錄，總體精度達到2分。開普勒選取了其中4個，其年份分別是：1587、1591、1593和1595年。經過計算，他發現軌道的中心不在太陽到偏心勻速點之間，盡管這一結果可以得到觀測支持，但用另一些觀測數據復驗時卻發現了偏差。于是，開普勒重新回到“托勒密假設”計算距離定律，即計算行星運動的速度和它到太陽的距離之間的關系（[2]，頁270）。但正圓與實際觀測到的數據不合，在圓周的側面要小一些。在用了兩年時間的多次嘗試之后，開普勒終于發現卵形比較合適。進而，他又將卵形調整為橢圓模型[7]。

從表面上看，開普勒是基于第谷的火星觀測數據得出行星運動的面積定律和橢圓定律。而實際上，開普勒所依據的火星沖位置的精確數據是建立在準確測定恒星位置之上的。開普勒剛進入第谷的研究團隊時，曾被派去輔助第谷的弟子隆戈蒙塔努斯（C. S. Longomontanus，1562—1647）解決火星運動問題，而這也被認為是開普勒以火星運動為切入點研究行星運動的主要原因。開普勒甚至還慶幸自己最初就找對了方向，否則可能永遠不能發現橢圓定律。

第谷自16歲起就開始進行恒星觀測，至51歲時，大概經歷了3個階段：前6年在萊比錫所做的工作價值不大;之后的7年，觀測結果雖不成熟，但大致可用;其28—50歲這21年間，他用力最勤，裝備最精，觀測精度最高。第谷盡其所能，細致地測定了所有肉眼可見的恒星位置，甚至包括六等星。他所測量數據的總體精度已達一弧分，有些甚至已到半弧分。為提高觀測精度，他還改進了一些觀測儀器，常用的測星儀器是一架“大六分儀”。六分儀是一架看上去有些像圓規的測量儀器，圓規的腳是由兩根長長的木條做成的“臂”，兩臂之間安有弧形的刻度盤。使用時，觀測者把兩臂分別瞄準要測量的兩點，然后在刻度盤上讀出所對應的弧度。在第谷的時代，六分儀是通用儀器，往往用來測量恒星之間的距離、恒星的方位以及地平高度。但第谷卻只用六分儀來測量恒星的地平高度。因此，他把儀器的一條臂固定在水平的位置上，從而基本排除由于觀測者手臂或身體的抖動而帶來的測量誤差。儀器的另一條臂可以繞固定端點活動，臂上有兩個視窗，觀測者可以用此校準視線，捕捉觀測目標。一旦確定，在臂的遠端的弧形刻度盤上即可讀出該目標的角高度。第谷用大六分儀測的精度高達24弧秒，而此前托勒密的精度大概在10弧分左右，哥白尼的在6—10弧分，從一定意義上說，第谷將觀測恒星的精度提高了20多倍（[2]，頁167—168）。這就為準確地觀測和記錄火星“沖”的位置打下了堅實的基礎，而這些數據正是開普勒建構橢圓軌道的經驗基礎。

二 古希臘的恒星觀測

第谷一直致力于改進的觀測方法早在古希臘時期就已形成。可以說，正是古希臘天文學傳統使得第谷對恒星觀測的改進成為可能。歐洲天文學以黃道坐標系為主，十二宮為基本坐標。最初的十二宮為星象，至古希臘時期，十二宮已成為固定于黃道的基本坐標。總體看來，《至大論》中所載恒星測算可以分為兩步。第一，確定位于黃道上的距星的準確位置;第二，通過渾儀測定某星相對于諸距星的位置（[8]，pp.251—253）。

關于第一步，《至大論》給出兩種方法，均與月亮位置的推算相關。第一種方法可以稱為“月食法”，因為月食時太陽正好處于與月亮相距180度的角度上，因此：

距星的經度=太陽在月食時的經度+從月亮到該星的經度差+180°（1）

（1）式右側第一項可通過日、月運動算法計算求得，第二項通過渾儀測得。此法在托勒密前的喜帕恰斯（Hipparchus， 公元前190—120）時期即已形成，需在發生月食時才能測算。為了打破此限制，托勒密發展出另一種方法，對應公式如下：

距星經度=太陽所在經度+從太陽到月亮的經度差+從月亮到所測星的經度差（2）

（2）式右側前兩項，有關太陽和月亮的經度，需要由天體運動算法計算而得。而第三項，需通過渾儀測定。或許正是這個原因，《至大論》中的恒星表位于月亮理論之后。而這也正是后來的哥白尼所批判的問題之一。然而在上面兩個公式中，還需加入月亮運動的修正值，主要包括兩項：首先是月亮東行的修正，因為月亮一天大概運動12°，每小時大概0.5°，這一變量不可忽略;另外，需考慮月亮的時差，也就是從地球表面和地心觀測的差異。《至大論》不但討論測量恒星的方法，還給出了測量實例，在第七章的第2節討論了測定獅子座距星經度的方法（[8]，pp.254—255）。

以上這些測算方法，是以歲差理論作為基礎。西方天文學之所以能在近代發生天文學革命，另一個主要原因是發展出一套精致的歲差理論。可以肯定的是，托勒密保留了關于喜帕恰斯有關歲差方面的工作。《至大論》明確指出，喜帕恰斯發現室女座α（Spica）的位置應該是在秋分點偏西6°，而在此之前提莫卡里斯（Timocharis，公元前320—260）觀測到此星的位置在秋分點偏西8°位置。關于提莫卡里斯，我們所知甚少，現在只能從《至大論》中獲得些許信息：他被認為是古希臘的系統天文觀測的奠基者，生活在亞歷山大里亞，其主要工作集中在公元前290—280年間。喜帕恰斯對歲差的判斷主要基于他和提莫卡里斯的幾次月食記錄，這些數據記錄在《至大論》中。其中還提到：至點和分點相對于恒星有一個恒定的西退，速度不超過每百年1度。

托勒密采用了喜帕恰斯的數據，即每百年1°的東移。除此之外，托勒密對獅子座（Regulus）也做了細致的觀測，主要基于月食觀測數據。他發現，相較于喜帕恰斯記錄的獅子座位置，他看到的似乎相對于至點有一個2°40′的東移，而他的觀測時間與喜帕恰斯之間相差265年，這就很接近百年差一度的移動速度。但與喜帕恰斯不同，托勒密認為整個恒星天球在東移，不僅是黃道上的至點和分點，所有恒星均有一個整體的東移傾向，速率約為百年1°。為探究恒星天球究竟是以黃極還是赤極為軸，托勒密引用由提莫卡里斯與喜帕恰斯的觀測數據，最終確定恒星東移不是沿赤道而是黃道。這一理論后來被納入到天球宇宙論，即諸恒星附著在恒星天球上，以100年1°的緩慢速率東移。

由此可見，托勒密時代確定了準確測定恒星的基本方法，發現恒星運行的基本規律。尤其重要的是，由于發現恒星東移規律，使得其后延續的數據可以不斷更新和改進。也正因此，第谷發現了不少前輩觀測方面的問題，并在改進中提升了觀測精度，這些為天文學革命打下了堅實的基礎。中國天文學的發展則與之不同，也體現在恒星觀測方法以及對恒星運動規律的認識方面。

三 古代中國的恒星觀測

科學史家席文（Nathan Sivin）先生指出，不同文明的人用幾乎相同的方法研究同樣的星空，其主要目的是為了搞清楚何時、何地發生了那種天象，但他們對星空的劃分以及這些劃分所暗含的基本理念是不同的，也正因此，不同文明創造了自己的星空[9]。西方天文學采用了十二宮的坐標體系，至托勒密時期，十二宮主要是對黃道而非星象的劃分。而之所以形成以黃道為主的坐標體系，這與古希臘人的觀測星空的方法有關。希臘人主要采用偕日法觀測星空，包括觀察恒星偕日升和偕日落，即觀測黃道附近的恒星在日出或日落后瞬間的升落[10]。

而中國古代天文學則以赤道坐標為主，主要以二十八宿為基本坐標系。準確地說，中國古代天文學采用的是一種北極—赤道坐標體系，北極居核心地位，赤道只起輔助作用。時圈從北天極向周圍展開，提供一種按時圈與赤道相截的點來劃分的赤道分區體系，即所謂的二十八宿。李約瑟（Joseph Needham，1900—1995）認為：中國古代的北極-赤道體系與小宇宙-大宇宙的思想背景有關，因為拱極星的上中天可用來指示看不到的宿的方位，《史記·天官書》中就有明確表述，如“杓攜龍角，衡殷南斗，奎枕參首”其含義是角宿的位置可以通過北斗七星斗柄的最后二星的位置確定，而斗魁的“頂”和“底”（即天權、天樞、天璣、天璇）的延長線與參宿相交[11]。這套體系的建立與古代中國的觀測方法有關，采用了與古代西方完全不同的沖日法，主要觀測永遠不升不落的極星和拱極星，也正因此古代中國的天算理論與子午線密切相關。二十八宿的界限一經劃定，在理解了天球的周日運動之后，由拱極星的上中天和下中天即可確定去天球赤道上每一點的位置。進而，通過望月時月亮的位置確定太陽在恒星間的位置，確定太陽和恒星的坐標關系。

與偕日法相比，沖日法有其優勢，主要由于地平線上的霧或其他大氣現象，偕日升和偕日落的準確時間可能難以確定。而沖日法最大的問題是忽略了對黃道體系的建構，因而難以對歲差現象有準確的理解由于歲差效應，北極點在緩慢移動，與之相應，如以恒星為參照，黃赤交點在沿黃道緩慢西退，從而導致恒星年與回歸年的不同，這就是中國古人所謂的歲差。。由于缺乏黃道體系的認識和使用，古代中國人缺乏對此現象的整體理解，盡管歷史上不乏對歲差現象的準確觀測，但都是比較零散的，缺乏整體性考慮。

古代中國歷算家一般將歲差的發現歸之于東晉的虞喜（約270—345）。主要依據是《大衍歷·歷議》中的“其七日度議曰：古歷，日有常度，天周為歲終，故系星度于節氣。其說似是而非，故久而益差。虞喜覺之，使天為天，歲為歲，乃立差以追其變，使五十年退一度”（[12]，頁2181）。虞喜是通過冬至日中星的觀測而發現歲差的。他把自己所做觀測結果與前人的記錄進行比較，發現冬至日黃昏出現于天空正南方的星宿明顯不同，唐堯時代冬至日昏中星是昴宿，而到了他的時代則變成了壁宿，虞喜把這種變遷歸因于冬至點連續不斷地西移。也就是說太陽在冬至所躔宿度逐漸西退所造成的。

在虞喜以前就有人注意到不同時代所測冬至點太陽所在宿度不同[13]。先秦時期《顓頊歷》記載冬至點在牽牛初度，西漢初年編制的《太初歷》雖仍沿襲了這個數值，但劉歆在《三統歷》中對此說頗有懷疑，他時而說“冬至，日月在建星”，時而認為在牽牛初度，甚至還說冬至“進退牛前四度五分”。東漢時賈逵根據元和二年（85）至元元年的實測，確定“冬至日在斗二十一度四分度之一”。但賈逵只是對冬至點的宿度做了改正，沒有意識到冬至點是運動的。從賈逵到虞喜間隔二百多年，冬至點又西移四度左右，虞喜之后的姜岌運用月食沖檢日度法，才精確地測得公元384年前后冬至點太陽已在斗十七度。

自東晉以來，中國長期用觀測昏旦中星的方法測定冬至宿度，這種方法必須有精確的時刻，若測量中星有差，則結果不準。南北朝時梁武帝大同九年（543）虞鄺對此有論：

然日之所在難知，驗以中星，則漏刻不定。漢世課昏明中星，為法已淺。今候夜半中星，以求日沖，近于得密。而水有清濁，壺有増減，或積度所擁，故漏有遲疾。臣等頻夜候中星，而前后相差或至三度，大畧冬至遠不過斗十四度，近不出十度。又以九年三月十五日夜半，月在房四度蝕。九月十五日夜半，月在昴三度蝕，以其沖計冬至，皆在斗十二度，自姜岌、何承天所測，下及大同日已卻差二度。（[12]，頁2198—2199）

由上可見，中星法其實是沖日法的一種具體應用，這在根本上與古希臘所用的偕日法不同。由于難以測定準確的夜半時間，不確定因素太多，古代天文家對歲差發現遲疑不定，甚至在積累充分證據后，還不敢承認。比如，唐初李淳風修歷時雖已注意到歲差現象，出于政治方面的考慮，在其所主持編修的《麟德歷》還未引入歲差。另外，他主持編修的晉、隋兩代的《天文志》和《律歷志》中對東晉虞喜發現歲差現象也只字未提。

繼虞喜之后，何承天（370—447）給出新的歲差值，大約每百年一度，與希帕恰斯-托勒密的數值比較接近，或許是受到了西方的影響[14]。然而，何承天并沒有把歲差應用到歷法中去，在他編制的《元嘉歷》中仍采用日數等于周天度數的陳規。中國歷史上，第一個把歲差引進歷法的是祖沖之（429—500），他在《大明歷》里把歲實同周天度區分開來，又把自己“參以中星，課以蝕望，冬至之日在斗十五”的結論與姜岌測冬至日在斗十七的結果比較，認為“通而計之，未盈百載，所差二度”，定出歲差值為“四十五年是一個月差一度”。“令冬至所在，歲歲微差”。使得日宿度和節氣的推算更加準確。祖沖之的做法遭到朝廷顯貴的非難，堅持“古歷冬至，皆在建星”，以此指責祖沖之引進歲差，是“虛加度分，空撤天路”“誣天背經”。祖沖之專門寫《駁議》一文據理駁斥。此后許多歷算家仍拘于陳法，不敢用歲差。

如以恒星為參照看黃赤交點或冬至點，其緩慢的西退應沿黃道而非赤道。祖沖之及其以前的歷算家所論多以赤道為宗。隋劉焯（544—610）首先提出了黃道歲差的概念，認為推算日月與五星的行度應該依據黃道度才更簡便和精確。然而，盡管劉焯的方法更科學，但由于缺乏充分的證據作為支撐，未得后世傳承。唐初傅仁均造《戊寅歷》引入歲差，遭到歷算博士王孝通的指責。李淳風甚至依據《堯典》四仲中星的內在矛盾，否認歲差現象的存在。

真正把歲差作為一個重要的歷算概念固定在歷法中得以流傳的是中唐時期的一行（683—727），其主持編訂的《大衍歷》為后世所宗。一行在隋劉焯基礎上重建歲差概念，繼承劉焯推算黃道日度的原理，主張“若上考往古，下驗將來，當據歲差，每移一度，各依術算，使得當時度分，然后可以步三辰矣。”但一行并不認同劉焯關于黃道歲差的概念，仍以推算赤道日度為據，計入歲差。《大衍歷·歷議》中有如下解釋：“所謂歲差者，日與黃道俱差也，……黃道不遷，日行不退，又安得謂之歲差乎？”由此可見，一行給出歲差的運動學機制，即黃道沿赤道西退。自此之后的歷法直到《大統歷》為止，都沿襲了《大衍歷》的傳統。如《授時歷》取赤道歲差為1分50秒，而黃道歲差為1分39秒，后者是赤道歲差值在黃道上的投影分量。

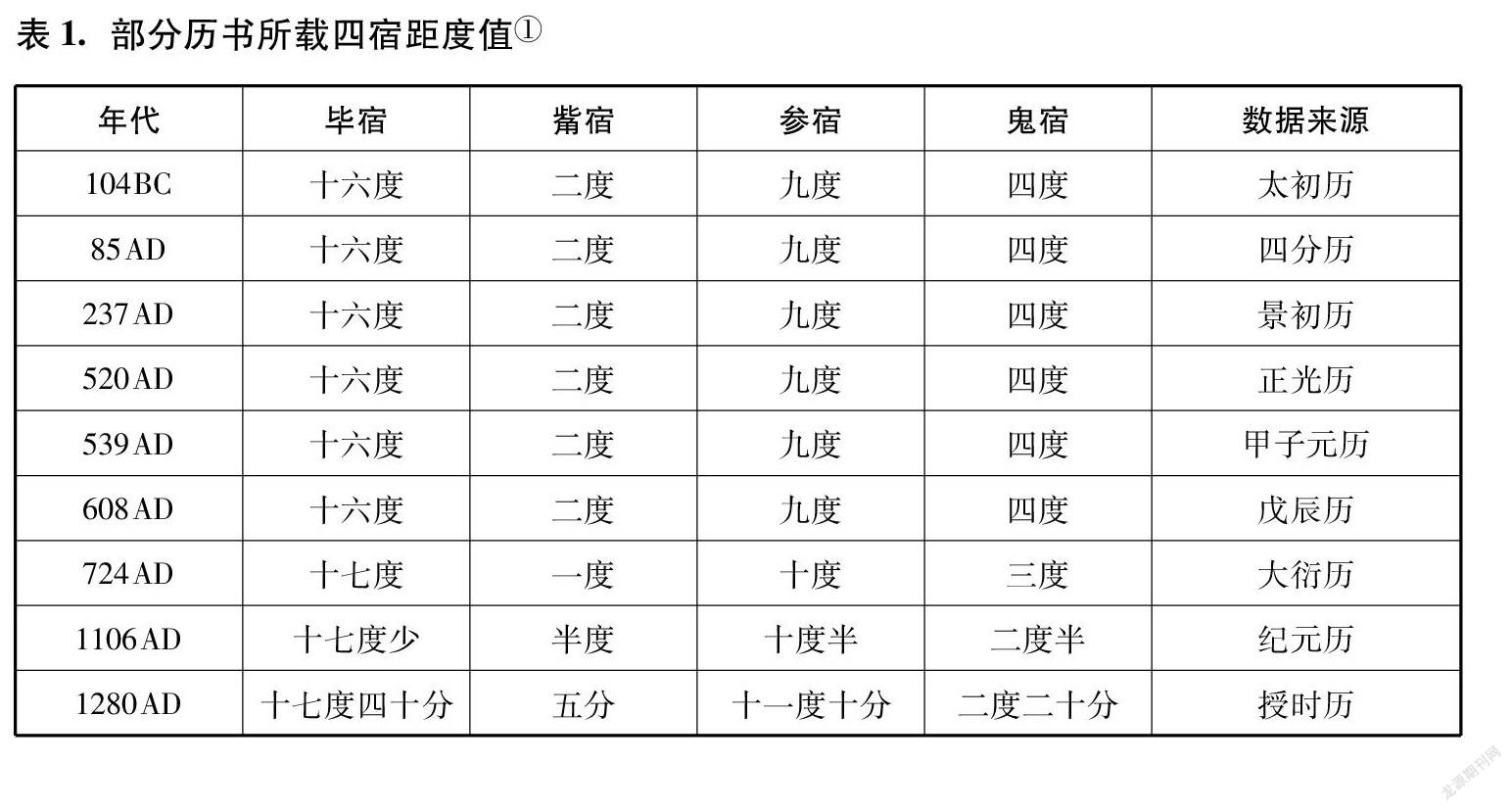
一行的歲差概念之所以產生如此影響，主要是由于他重新厘定了二十八宿的距星，測量了距度和去極度，與古法不同。唐初貞觀年間，李淳風也曾注意到二十八宿距星相較古測已有變化。但在這個問題上，李氏比較保守，在其主持修撰的《麟德歷》中，依循舊法。一行發現二十八宿中畢、訾、參、鬼四宿的距度與古代不同（[12]，頁2225）。表1對部分歷書所載四宿距度值進行比較。

另外，一行還發現二十八宿去極度的變化，即從牛宿到井宿，古大今小，其間稍有差異的是女宿（古小今大）和危宿（古今相同）;從鬼宿到斗宿，古小今大，其中稍異者僅有鬼宿（古今相同）。一行將自己觀測的二十八宿去極度的數據（今測）與《石氏星經》中的（舊測）相比，發現上述的變化規律。《石氏星經》收錄于瞿曇悉達所著的《開元占經》當中，大約成書于開元六年（718）前后，對一行來說是非常重要的參考。

一般認為，古希臘人由于亞里士多德的天球理論，認為天界的變化是不可接受的，因而他們對一些明顯的異常天象，如超新星和黑子等，都視而不見，或見而不錄。所以，從古代西方的天象記錄中很難找到這些違背常理的記錄。而古代中國由于沒有類似西方的宇宙論對天文觀測的約束，加之異常現象對星占而言有重要意義，因此許多異常現象被忠實記錄下來。盡管如此，中國古代天文學中也存在視而不見、見而不述的情況，比如歲差，其實早在漢代時即已發現冬至點太陽所在宿度已與之前春秋時期有很大不同，但直到東晉虞喜（281—356）才指出存在回歸年與恒星年不同的歲差現象。與之相應的，二十八宿距星，由于歲差效應，也在不斷地移動。但從漢至唐700多年的時間里，沒有人提出調整，直到中唐時期的一行方才改觀。之所以有如此差異，是因為希臘人更加關注發現天體運行規律。歲差現象，盡管短時期看并不明顯，但時間一長，即呈現出規律性的變化。歲差理論后來被納入到天球體系之中，恒星天球的主要運動。而中國古代天文學，盡管對變化性現象非常關注，但對于一些固有觀念，例如年的概念，二十八宿的距星等，是不容有變的。

四 結語

袁敏等曾以“如果開普勒是中國人”為題討論中西方數理天文學的差異，認為中國古代數理天文學偏重數值算法的創造，缺乏對幾何模型的建構，而以古希臘為源頭的歐洲天文學則正好相反。她們認為，對于熟悉圓錐曲線并強調幾何模型的人來說，可以根據一行的太陽視運動中心差算法推導出橢圓模型[15]。言下之意，一行的太陽視運動算法邏輯上可以推演出橢圓模型，導致中國古代天文學家未發現橢圓定律主要原因是中國古代歷算家缺乏圓錐曲線的認識。但是，開普勒并不是根據太陽的視運動，而是基于火星運動數據構建了行星的橢圓模型。而數學上偏心等速點模型和橢圓模型是等價的，也就意味著，根據《至大論》中任何一個行星的運動模型在理論上都可以推演出橢圓模型。那么何以開普勒未根據其他行星的運動發現橢圓規律，慶幸從火星研究中發現了新天文學的曙光呢？我們還是要回到恒星觀測數據方面，可以肯定，如果沒有第谷的恒星觀測數據，開普勒是無法發現“真實”的宇宙結構的。

恒星觀測是古代中西方天文學的一個主要區別，體現在觀測方法及所用主要坐標系這兩方面。古希臘采用偕日法，確立了以黃道而非恒星為主的坐標體系。而古代中國采用的是沖日法，更關注極星和拱極星的位置變化，致力于建立一套以北極-赤道坐標系為主，以具體的恒星背景作為參照的坐標系。由于歲差效應，全天恒星沿黃道有一個東移，致使北極和二十八宿距星在長時段內是運動的。由于缺乏對歲差本質的認識，中國古代的恒星觀測非常混亂。中國古代天算家往往采取含糊其辭的應對策略：一方面通過不斷觀測確定準確的恒星背景;另一方面為了尋求與古代傳統數據的契合，不得不遷就一些陳舊的觀念或說法。而西方天文學建立了以黃道坐標為主的坐標系，采用十二宮坐標系，黃道坐標固定不動，以此為參照，認識到恒星沿黃道東移的規律，這就為整個數理天文學的發展提供了堅實的基礎。

古希臘天文學家很早就發現恒星東移的規律，表面上具有一定的偶然性，即恰好古希臘天文學家采用了從古巴比倫繼承的黃道坐標系，而諸恒星正好存在一個沿著黃道的運動。但是實際上，托勒密等在得知恒星有緩慢的東移運動后，曾探尋這種運動究竟是沿著赤道還是黃道運動，即尋找這種緩慢運動的軸。在找到確鑿的證據后，最終才確認恒星是沿黃道東移[16]。古希臘時期發現的恒星運動的確定性，不僅為行星運動提供了準確的參考，更重要的，使得后來的觀測可以不斷地對前人進行修正。比如，哥白尼之所以對托勒密星表提出批判，主要是他已得知伊斯蘭天文學家對托勒密星表的修正。而第谷正是在改進儀器的基礎上，對托勒密的星表做了完整的修正和補充。恒星數據的確定性還使得第谷對托勒密星表數據是否真的由托勒密本人所做產生了懷疑。因為盡管托勒密宣稱其星表中的數據是他本人所測，但第谷懷疑，《至大論》中的數據是從喜帕恰斯星表數據改編而來的，即黃緯保持不變，而黃經按照每百年差一度做一定的調整。當然，第谷并沒有找到確鑿的證據，重要的是很難找出喜帕恰斯留下的星表數據。因此，這一爭議持續四百多年，至今尚無定論。盡管如此，古代西方恒星數據的確定性，實際上給后人推算往古提供了可能性。因此，托勒密時期所確立的星表數據是可以證偽的，這也就使得后人可以在前人的基礎上不斷地提高測算經度，更新數據。最終開普勒基于第谷更為準確的星表得出了行星運行的規律，開啟了新天文學的篇章。

參考文獻

[1] 康德. 純粹理性批判（注釋本）[M]. 李秋零（譯注）. 北京： 中國人民大學出版社， 2011. 11.

[2] 吳以義. 從哥白尼到牛頓： 日心說的確立[M]. 上海： 上海人民出版社， 2013.

[3] Grahoff G. The History of Ptolemys Star Catalogue[M]. New York Berlin Heidelberg： Springer-Verlag， 1990. 23.

[4] Swerdlow N M， Neugebauer O.. ?Mathematical Astronomy in Copernicuss De Revolutionibus[M]. New York Berlin Heidelberg Tokyo， 1984. 121—123.

[5] Duncan A M.. Copernicus： On the revolutions of the heavenly spheres. A new translation from the Latin with introduction and notes[M]. David & Charles： Newton Abbot London Vancouver， 1976. 103—139.

[6] Copernicus N.. Three Copernican Treatise[M]. translated by Rosen E. Dover Publications， 1959. 57.

[7] Kepler J.. New Astronomy[M]. translated by Donahue W H. Cambridge： Cambridge University Press， 1992. 575.

[8] Evans J.. The History and Practice of Ancient Astronomy[M]. New York and Oxford： Oxford University Press， 1998.

[9] Sivin N.. Granting the Seasons， the Chinese Astronomical Reform of 1280， With a Study of Its Many Dimensions and an Annotated Translation of Tis Records[M]. Springer， 2009. 7.

[10] Needham J.. Science and Civilisation in China. V3 Mathematics and the Sciences of the Heavens and the Earth[M]. Cambridge University Press， 1959. 229.

[11] 朱文鑫. 《史記·天官書》恒星圖考[M]. 上海： 商務印書館， 1934. 11—12.

[12] 歐陽修. 新唐書·歷志[A]. 歷代天文律歷等志匯編·第七冊[C]. 北京： 中華書局， 1976.

[13] 何妙福. 歲差在中國的發現及其分析[A]. 科學史文集（1）[C]. 上海： 上海科學技術出版社， 1978. 22—30.

[14] 鄭誠. 何承天歲差考[J]. 上海交通大學學報（哲學社會科學版）， 2007，（1）： 50—57.

[15] 袁敏， 曲安京. 假如開普勒是中國人[J]. 自然辯證法通訊， 2008，（1）： 69—74.

[16] Ptolemy. Ptolemys Almagest[M]. translated by Toomer G J.. Gerald Duckworth， 1984. 260—261.

Star Observation and the Astronomical Revolution

WANG Guangchao， ZHENG Han

Abstract：Based on the comparison between ancient Chinese and European stellar observation technologies and related theories， this article tries to explain why the new astronomical revolution occurred in Europe instead of China. The conclusion is： the new astronomical revolution in modern Europe mainly benefited from the observation technology of contiguity and the zodiac system during the ancient Greek period. Ptolemy who edited Almagest already had a clear understanding of the phenomenon of precession， which enabled Tycho to create a more sophisticated star catalog which was an important basis for Kepler to figure the planet ellipse law. In contrast， Chinas star observations use the method of opposability and 28 lunar lodges coordinate system. Due to the lack of accurate understanding and explanation of the precession effect， ancient Chinese astronomical theories are fundamentally uncertain. All this does not support an astronomical revolution in modern China like that in Europe.

Keywords：Star observation， Ptolemy， Tycho， Kepler， astronomical revolution