供水系統智能管理模型研究

張婷

（長春汽車工業高等專科學校，吉林 長春130000）

1 問題背景

當前校園供水系統主要采取智能水表以獲取實時供水系統運行數據，而保障校園供水系統的正常運行則需要投入大量的人力、物力和財力。為有效降低損耗，根據2020 年全國大學生數學建模競賽E 題提供的數據，本文通過數據挖掘建立數學模型，及時發現和解決供水系統中存在的問題，有效提升了供水系統的智能管理水平。

2 數據的預處理

首先借助Access 數據庫對賽題中所給數據進行了預處理：數據清洗-抽取-整合，對于大量的水表信息數據進行以下預處理：

2.1 剔除數據表中無關數據；

2.2 將水表數據按功能分區，將水表數據與用戶號相關聯，篩選出用水的用戶明細，剔除沒有用水的用戶明細；

2.3 將附件一季度、二季度、三季度、四季度的數據整合，分別篩出各功能區全年的水表數據。

3 供水系統智能管理模型

3.1 校園水表數據的描述統計分析

通過統計描述水表數據的變化規律，并給出校園內不同功能區（宿舍、教學樓、辦公樓、食堂等）的用水特征：

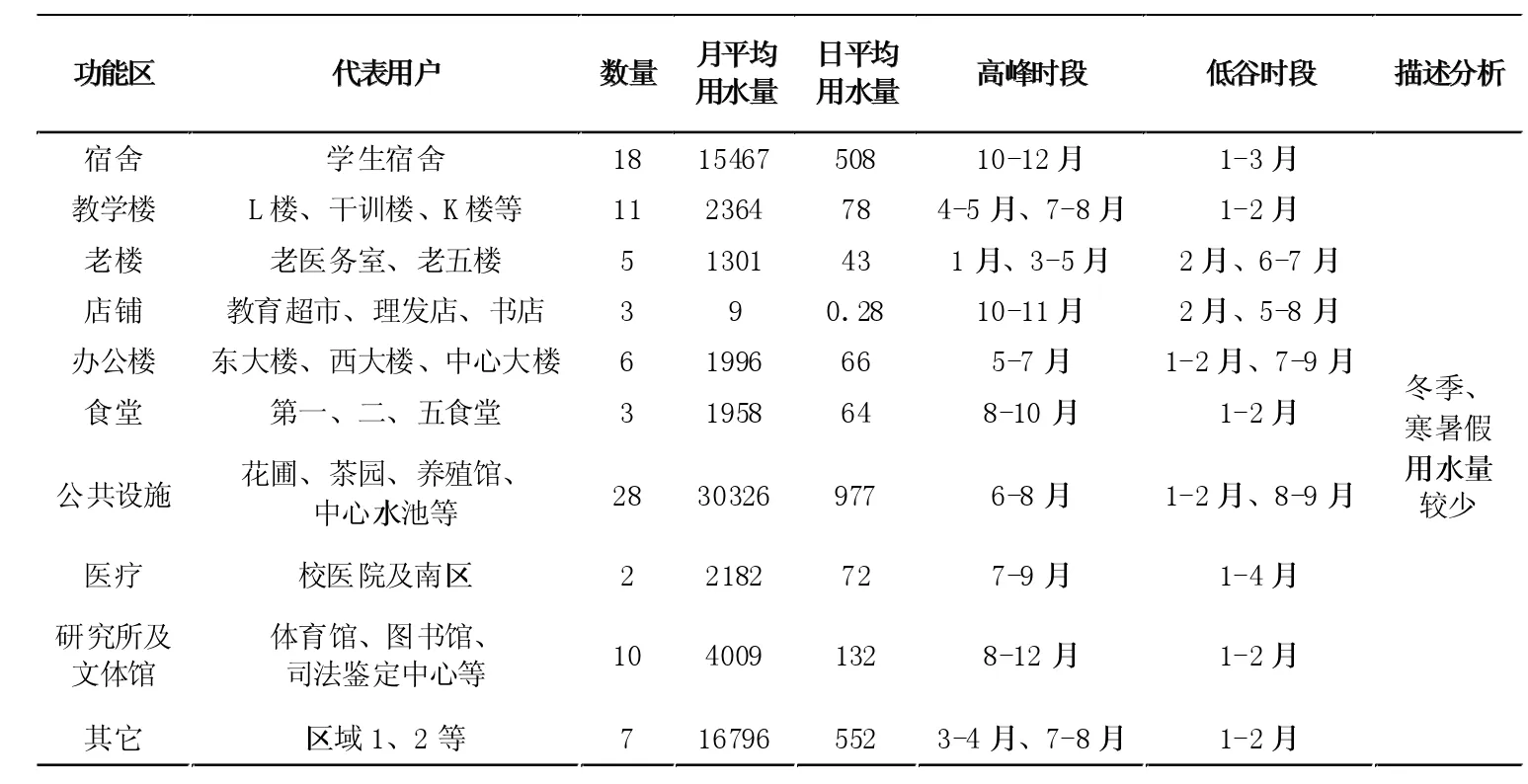
表1 各功能區全年用水數據描述統計

由表1 可知宿舍、教學樓、食堂、公共設施、辦公樓等區域在1-3 月和7-9 月用水量較少，我們可推測因學生寒暑假所以導致用水量減少；醫療、宿舍體育館，店鋪等區域在5-6 月和7-9月用水量較大，我們可推測因夏季天氣炎熱為感冒高發時期所以醫院和人流量大的功能區用水量激劇增加。

3.2 建立水表層級關系與水表數據的關系模型

通過題中數據作層級水表年用水總量的分布圖（圖1）。

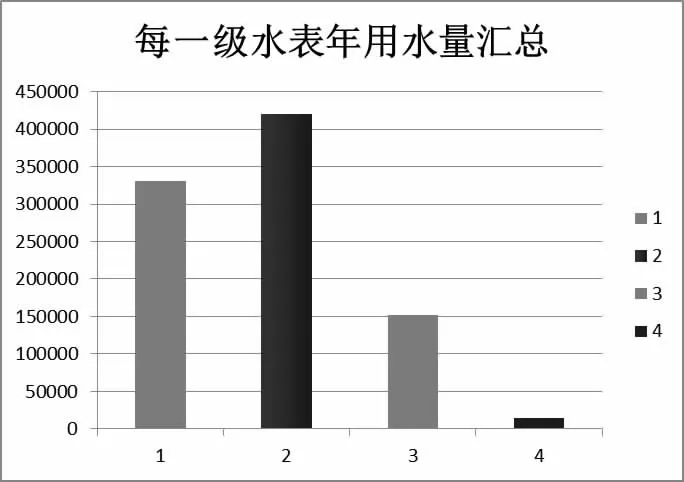
圖1

由圖可知第二級年用水總量最多，第四級年用水總量最少。進一步分析水表數據與水表層級之間的關系，我們用回歸分析的方法建立數學模型：

設Pi為每一層的年用水量，i=1，2，3，4；Tij：表示第i 個層級的第j 個子層級的年用水量。

代入數據，令回歸平方和取得最小值即認為回歸方程的擬合效果最好。根據二元函數求極值的方法確定回歸系數，擬合后的回歸方程為：P贊=312904x+1203473。

利用相關系數檢驗法、F-檢驗、T-檢驗來進行回歸方程擬合優度和顯著性的檢驗。根據模型匯總表格得到R2=0.971，接近于1，因變量與自變量之間的線性相關程度較強，擬合優度很好。F 的P 值為0.0225，小于0.05，顯然F>F鄣，回歸方程的線性關系顯著。

3.3 供水管網漏損評估數學模型

針對題中所給數據進行深度挖掘，基于DMA 分區管理的思想主要采取水平衡分析法、夜間最小流量分析法建立數學模型評估校園管網漏損水平。

3.3.1 水平衡分析法

3.3.2 夜間最小流量法

基于DMA 分區域進行管網管理的思想，通過分析劃定區域內夜間最小流量的方法來分析校園管網的漏損情況。

3.3.2.1 夜間最小流量時段的確定

根據在第一問中劃定的校園用水區域，通過智能水表實時監測獲取的用水量數據，利用統計學方法確定了該校園夜間最小流量時段為：1:00～4:00。

3.3.2.2 夜間最小流量基準的確定

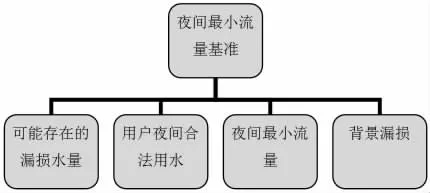
圖2

3.3.2.3 夜間最小流量

一般情況下在夜間最小流量時段，區域內用戶用水量最少，智能水表的流量讀數應該僅包括用戶合法夜間供水、管網漏損水量及背景漏損幾個部分，而這部分的用水流量波動范圍很小，水表讀數是相對穩定的。因此，將區域內用戶夜間最小流量做如下定義：

L夜間最小流量=Min{當前測定流量數值，用戶年度夜間最小流量時段的最小值}

3.3.2.4 用戶夜間合法用水量

針對該指標采取統計學方法，應用數據挖掘技術得到代表該校園年度平均用戶夜間合法用水量。

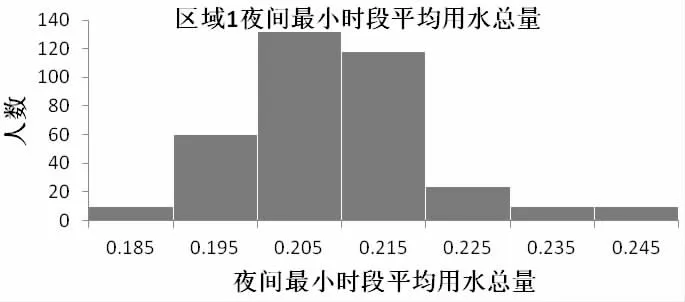
圖3 區域1 夜間最小流量時段平均用水總量概率分布圖

根據題中所給數據，按照前面劃分的10 個DMA 區域的年度夜間用水量的智能水表獲取的數據分析得具有代表性的區域平均用戶夜間合法用水量。

通過圖3 看出該區域內間最小時段平均用水總量呈中間高，兩邊低的概率分布近似服從正態分布。根據正態分布的3σ準則，我們采用95%置信區間的下限作為該區域用戶年度平均夜間合法用水量。

3.3.2.5 夜間漏損水量

根據前面的數據分析，我們定義區域內某時刻夜間漏損水量為：

3.3.2.6 漏損判定的參數閾值

通過對題中數據的挖掘與分析，我們確定在一定時間間隔內的夜間合法用水量的平均差為漏損判定的參數閾值：

3.3.3 爆管漏損

我們認為在某一時段水表讀數出現陡增，即超過該區域同時段歷史平均水平的β 倍，就視為爆管漏損。通過對劃定區域日用水量變化趨勢的分析，規定β叟10 時即為爆管漏損。

建立的漏損判定的數學模型，通過對智能水表獲取的實時用水量數據的分析，首先確定了爆管漏損的信息，然后做出了校園暗漏的位置判定。

4 模型的評價與推廣

供水系統的智能管理研究具有現實意義，本文運用Access數據庫、SPSS 軟件、Excel 等軟件對數據挖掘分析進而建立數學模型，降低了損耗的同時有效提升了供水系統的智能管理水平。