基于科創(chuàng)板波動性的實證研究

郭建峰，白瑜瑜

(1. 西安郵電大學經(jīng)濟與管理學院，陜西 西安710061；2. 英國雷丁大學亨利商學院，雷丁RG6 6AH)

一、 引言

2018 年11 月5 日，習總書記在中國首屆上海國際進口博覽會開幕式上提出設立科創(chuàng)板并在上海試點注冊制。 該板塊是獨立于現(xiàn)有主板市場的一個新設板塊，實現(xiàn)了我國科技型和創(chuàng)新型中小企業(yè)融資的重大制度創(chuàng)新。

波動性被認為是最能反映金融市場資產(chǎn)價格變化的基本特征之一，所以適當?shù)牟▌有砸呀?jīng)成為衡量當前金融市場健康運行最直接、最簡單的指標。 2019 年7 月22 日，科創(chuàng)板正式掛牌上市。 由于市場還不夠成熟，交易數(shù)據(jù)較少，用傳統(tǒng)交易數(shù)據(jù)建模分析的方法不能夠很好地分析和預測科創(chuàng)板的波動性。 根據(jù)當前市場的實際交易情況，由于單一模型的結(jié)果過于武斷，對問題的分析過于片面以及結(jié)合實際交易情況，使用R 語言和Winbugs 軟件對SV-N 和SV-T 模型進行貝葉斯分析，采用MCMC 方法來擬合科創(chuàng)板市場的波動性。

二、 文獻綜述

呂紅兵和朱奕奕認為我國證券市場參與者應重新審視和構(gòu)建自身的監(jiān)管職能，進而形成一種高效且合理的監(jiān)管，實現(xiàn)政府和市場之間的互動。 黃登仕和王輝認為科創(chuàng)板作為一種新的制度供給對我國經(jīng)濟高質(zhì)量發(fā)展具有重要的作用，但存在缺陷，他們提出了從各個方面完善科創(chuàng)板制度供給的對策。 張群輝通過對雙重股權(quán)結(jié)構(gòu)背后的機制進行分析，得出：科創(chuàng)板應該在信息披露、股權(quán)轉(zhuǎn)讓等方面制定相關的規(guī)定來保護投資者利益。

姚德權(quán)和曹海毅采用派許加權(quán)平均法編制我國A 股傳媒業(yè)振興指數(shù)，通過實證得出該指數(shù)能夠很好地反映股票價格的波動，具有實際應用價值。 王源昌等采用派式加權(quán)法編制云南板塊指數(shù)，通過實證分析得出該指數(shù)反映了云南上市公司股票的整體波動情況，且走勢和滬深300 指數(shù)走勢一致。 一般來說，指數(shù)編制的方法有算術平均法、幾何平均法和加權(quán)平均法。 與前兩種方法相比，加權(quán)平均法更能真實地反映出市場的整體走勢。

杜俊娟通過上證指數(shù)的農(nóng)業(yè)股信息，運用MCMC 方法研究隨機波動模型對于農(nóng)業(yè)經(jīng)濟的波動性影響。 張靜和張旭以招商銀行理財產(chǎn)品為研究對象，采用不同的SV 模型研究收益率波動性，結(jié)果表明SV-T 模型對于研究收益率波動性有顯著的效果。 趙慧琴和劉金山用MCMC 方法研究上海股市的波動性，結(jié)果表明：SV-T 模型可以更好地適應上海股市的“尖峰厚尾”特征。

但是，目前關于科創(chuàng)板波動性實證研究的相關文獻較少，大多數(shù)都是介紹科創(chuàng)板市場以及科創(chuàng)板上市的各種制度、準則等，所以無法在前人的基礎上來參考研究。 論文選取從2019 年7 月22 日到9 月30 日首批上市的25 家公司10分鐘的高頻交易數(shù)據(jù)科學構(gòu)造指數(shù)，采用基于MCMC 模擬的貝葉斯方法進行實證分析。

三、 模型原理

論文的模型構(gòu)建將基于以下的理論基礎。 研究收益率波動性主要采用兩類模型：自回歸條件異方差模型(ARCH模型)和隨機波動模型(SV 模型)。 Taylor 在1986 年解釋和研究金融產(chǎn)品收入序列波動率的自回歸行為時提出的隨機波動率模型，稱為SV 模型。 SV 模型將波動率視為不可觀察的隨機過程，新的隨機變量被添加到SV 模型中，使得長期波動率預測和波動序列穩(wěn)定性的擬合效果優(yōu)于傳統(tǒng)ARCH 模型。 長期的研究結(jié)果表明，相對于ARCH、GARCH 模型，SV模型對于新興交易市場尤其是剛剛設立的交易市場波動率的預測具有很好的適應性。

考慮到我國科創(chuàng)板市場于2019 年7 月22 日開始正式交易，無論是交易股票數(shù)量還是交易額都處于成長階段，積累的交易數(shù)據(jù)有限，市場尚未成熟，交易制度尤其是監(jiān)管制度也在逐步完善，且剛剛上市交易的股票價格波動明顯，故論文最終選用SV 模型來研究科創(chuàng)板市場收益率的波動性。

(一)隨機波動模型

在討論隨機波動模型時，Taylor 在討論和解釋不同金融資產(chǎn)的預期收益序列的自回歸行為時，引入了標準的SV 模型，簡稱SV-N 模型。 其形式如式(1)所示。

標準SV 模型：

式(1)中，SV 模型的波動率是由均值方程和波動方程組合構(gòu)成。 其中，SV 模型的波動率是對數(shù)形式的波動率。yt表示t時刻的波動率；εt為獨立同分布的白噪聲干擾，服從正態(tài)分布N(0，1)；ηt是獨立同分布的波動的擾動水平，服從正態(tài)分布N(0，τ2)。 在標準SV 模型中誤差項ηt與εt都是一個不可能被觀測的值，且二者之間不具有任何的相關性。

為了描述金融交易波動數(shù)據(jù)的“尖峰厚尾”的特征，Kim等將標準SV 模型擴展為一般模型，稱為厚尾SV 模型(SVT)。 該模型能夠從時間序列中捕獲“尖峰厚尾”的特征。 其形式如式(2)所示。

厚尾SV 模型：

式(2)中前兩個模型式子的含義與SV-N 模型一致，第三個式子明確地描述了金融數(shù)據(jù)“尖峰厚尾”的特征，當4＜?＜∞時，t分布的峰態(tài)系數(shù)大于3，?→∞時就為正態(tài)分布，?＜4時其峰態(tài)系數(shù)不存在。

(二)隨機波動模型估計

SV 模型可以很好地刻畫金融交易數(shù)據(jù)的特征，在金融研究領域應用廣泛。 論文基于經(jīng)典的貝葉斯原理構(gòu)造SV 模型的后驗分布，然后通過Gibbs 抽樣方法估計SV 模型的參數(shù)和分析其波動性。

1. 貝葉斯推斷

貝葉斯推斷的基本思想：若θ為一個待估參數(shù)或向量，樣本為x1，x2，…，xn，以p(x1，x2，…，xn｜θ)為樣本x1，x2，…，xn對θ的條件密度，稱為似然密度函數(shù)，h(θ｜x1，x2，…，xn)表示θ對x1，x2，…，xn的條件似然密度，即后驗分布密度，貝葉斯公式如下：

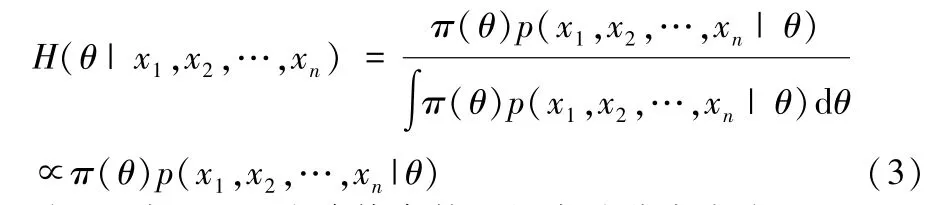
式(3)中，π(θ)為待估參數(shù)θ的先驗分布密度。 即通過h(θ｜x1，x2，…，xn)推斷出待估參數(shù)θ，也可以對待估參數(shù)θ進行估計和檢驗。

2. MCMC 模擬

MCMC 的原理：給定隨機數(shù)學過程{Xt}，假設每個貝葉斯Xt的值為狀態(tài)空間?中任意一個貝葉斯值。 若我們給定一個Xt值，Xh值不隨著Xs值的變化而變化，s＜t，這樣就把該隨機過程{Xt}稱為馬爾可夫過程。 即如果隨機數(shù)學過程{Xt}是馬爾可夫過程，則該隨機數(shù)學過程的條件分布函數(shù)必須滿足以下式子：

如果{Xt}過程是離散的隨機過程，則式(4)可以變成

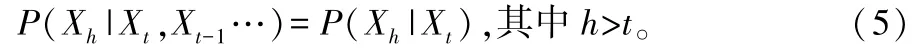
設A為狀態(tài)空間?中的一個子集，則轉(zhuǎn)移概率函數(shù)Pt(θ，h，A)＝P(Xh∈A｜Xt＝θ)(h＞t)為馬爾可夫過程的一個轉(zhuǎn)移概率函數(shù)。 如果該過程中轉(zhuǎn)移概率只是依賴于h-t而不依賴于t，那么稱該馬爾可夫過程有一個穩(wěn)定的轉(zhuǎn)移概率分布。

3. Gibbs 抽樣

Gibbs 抽樣原理：假設一個n維隨機變量向量θ＝(θ1，θ2，…，θn)，不知道其聯(lián)合分布，只知道每個隨機變量θi在給定其他隨機變量的條件下滿足條件分布θ＝(θi｜θ1，θ2，…，θn)，這時就可以直接使用Gibbs 抽樣。 假設給定一組初始值θ0＝(θ1.0，θ2.0，…，θn.0)，則這個抽樣過程可以表示為：

從分布p(θ1｜θ2.0，…，θn.0)中抽取θ1.1；

從分布p(θ2｜θ1.0，θ3.0，…，θn.0)中抽取θ2.1；

……

從分布p(θn｜θ1.0，θ3.0，…，θn-1.0)中抽取θn.1，這樣就完成了一次Gibbs 迭代，得到了θ1＝(θ1.1，θ2.1，…，θn.1)。

重復上述步驟，就可以得到θ1，θ2，…，θn，去掉前m次得到剩下的θm+1，θm+2，…，θn，當m足夠大時，就可以把θm+1，θm+2，…，θn看成是分布p(θ｜X)，這樣就可以根據(jù)此序列來做統(tǒng)計推斷，即

四、 實證分析

論文選用科創(chuàng)板開市以來第一批掛牌上市的科創(chuàng)板企業(yè)，2019 年7 月22 日開盤到9 月30 日期間每隔10 分鐘的股票收盤價作為基礎數(shù)據(jù)。 用加權(quán)平均法構(gòu)建科創(chuàng)板指數(shù)(簡稱為“科指”)，采用加權(quán)平均法編制指數(shù)，簡單易懂，便于計算，同時，這也是很多指數(shù)包括上證指數(shù)構(gòu)建的方法。 根據(jù)各個上市企業(yè)在科創(chuàng)板市值所占的比重來構(gòu)建該科創(chuàng)板指數(shù)，具體公式為：

使用SV 模型建模時，通常使用對數(shù)收益率：yt＝100×(lnpt-lnpt-1)，pt表示在t時刻科創(chuàng)板指數(shù)的收盤價，yt表示t時刻股票的對數(shù)收益率。 論文統(tǒng)計和研究所用數(shù)據(jù)均來源于Wind 數(shù)據(jù)庫，所用的軟件為WinBUGS14。

(一)標準SV 模型建模

在標準SV 模型中，每個先驗參數(shù)都是獨立的。 參考古典物理學者Kim 對標準模型中各參數(shù)的先驗分布假設，對各參數(shù)的先驗分布分別做如下假設：

設φ＝2×φ?-1，其中假設先驗參數(shù)φ?服從分布Beta 分布φ(φ(1)，φ(2))，于是先驗參數(shù)φ的先驗分布表示為

其中，超參數(shù)φ(1)的初始值為20，φ(2)的初始值為1.5。參數(shù)μ的先驗分布當且僅當服從于正態(tài)分布N(μ?，σ2?)，其中超參數(shù)μ?取0，σ2?取100。 參數(shù)τ2的先驗分布服從于逆分布取為Gamma 分布IG(σr和sσ)，其中超參數(shù)σr和Sσ分別取為2.5，0.025。

SV-T 模型中多了參數(shù)ω，先驗分布為ω～(8)I(4，40)。

(二)厚尾SV 模型建模

與標準SV 模型類似，在Gibbs 采樣過程中獲取初始值μ＝0，φ＝0.95，τ＝0.02，ω＝-0.6。 為了確保其參數(shù)的收斂性，對每個參數(shù)進行10000 次迭代并退火，舍棄前500 次迭代后各參數(shù)達到收斂狀態(tài)，通過Gibbs 抽樣，得到每個參數(shù)的估計值。

表1 為SV-T 模型各參數(shù)的均值、標準差、MC 誤差、2.5%分位數(shù)和97.5%分位數(shù)的貝葉斯值。 據(jù)Gibbs 抽樣，獲得每個參數(shù)的估計值：

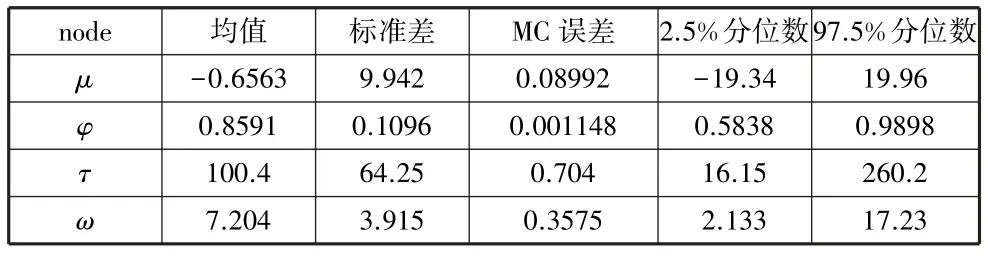
表1 SV-T 模型中科指10min 數(shù)據(jù)的參數(shù)估計值

(1)在SV-T 模型中科指10min 數(shù)據(jù)的自由度參數(shù)ω的值為7.204。

(2)在SV-T 模型中科指10min 數(shù)據(jù)的波動水平參數(shù)μ為-0.6563，波動持續(xù)性參數(shù)φ為0.8591，參數(shù)τ的貝葉斯參數(shù)估計值為100.4。

和SV-N 模型不同的地方是，SV-T 模型中加入了自由度。 從圖1 可以明顯地得出：SV-T 模型中10min 數(shù)據(jù)參數(shù)ω的擬合效果更形象。 采用MCMC 方法進行模擬估計的參數(shù)值是準確的。

圖1 科指10min 數(shù)據(jù)SV-T 后驗分布密度函數(shù)仿真圖

五、 結(jié)論

論文通過對收盤價進行指數(shù)構(gòu)造，以10min 高頻數(shù)據(jù)作為樣本，采用SV-N 和SV-T 模型來研究科創(chuàng)板的波動性。通過貝葉斯原理，構(gòu)造基于Gibbs 抽樣方法的MCMC 模擬仿真過程，并對兩個模型進行實證分析，結(jié)果均表明：科創(chuàng)板指數(shù)收益率波動較大且持續(xù)時間較長，且SV-T 模型的擬合效果明顯優(yōu)于SV-N 模型。

通過對收益率波動性的綜合分析，可以很好地評估和預測金融風險。 科創(chuàng)板是新設立的一個板塊，對于投資者來說，應當充分了解和掌握各種交易制度，加強風險識別能力，學習相關專業(yè)知識，進而進行準確、合理的投資；對于監(jiān)管者來說，科創(chuàng)板制度的創(chuàng)新導致價格資產(chǎn)波動明顯，給監(jiān)管者帶來了一定的挑戰(zhàn)，另外科創(chuàng)板收益率波動性明顯，這就要求加強信息披露和投資者與上市公司之間的溝通；對于機構(gòu)投資者來說，科創(chuàng)板“尖峰厚尾”的特性吸引了更多的投資者參與進來，而這種虹吸效應，使得其他市場資金回流到科創(chuàng)板市場，引發(fā)了各個市場對機構(gòu)投資者的爭奪，造成更大的波動性和流動性；對于研究人員來說，目前上市公司不多，股票數(shù)量不夠，數(shù)據(jù)交易時間較短，這都將對研究科創(chuàng)板收益率波動性產(chǎn)生影響。 隨著科創(chuàng)板市場的不斷交易，交易數(shù)據(jù)和上市公司將不斷增加，這會使得對科創(chuàng)板市場波動性的研究具有更堅實的基礎。