基于小波分解和IIR濾波器的最優(yōu)均衡器設(shè)計

梁 彥，凌永權(quán)

（廣東工業(yè)大學(xué) 信息工程學(xué)院，廣東 廣州 510000）

1 研究背景

均衡器是一種以補償方式修補傳輸系統(tǒng)固有缺陷，減少傳輸系統(tǒng)對輸入信號造成的失真的電子設(shè)備，通常通過一組濾波器以串聯(lián)或者并聯(lián)的方式實現(xiàn)［1］。均衡器可以顯著提高音頻的質(zhì)量，因此被廣泛應(yīng)用于音樂會和廣播等音頻傳輸系統(tǒng)。

均衡器一般關(guān)注中心頻率、帶寬及增益3個重要特征。根據(jù)這3個特征是否可調(diào)，可將均衡器分為圖示均衡器和參數(shù)均衡器兩個類別［2］。通過預(yù)設(shè)圖示均衡器濾波器組中每個濾波器的中心頻率和帶寬，使用者只需調(diào)整濾波器增益即可實現(xiàn)信號的均衡化，使用方便簡單［3］；參數(shù)均衡器的每個濾波器的中心頻率、帶寬及增益都是可控的，使用靈活度更高，也能實現(xiàn)更高精度的均衡化，但使用者需要具備一定的專業(yè)知識［4-6］。由于使用簡單、方便明了，圖示均衡器被廣泛應(yīng)用于人們的日常生活［7］。

一般情況下，為了彌補精度上的不足，圖示均衡器會將音頻通頻帶切分為多個不同的頻段，其中一個濾波器負(fù)責(zé)處理一個頻段的均衡化［8］。例如，房間均衡器將音頻通頻帶切分為32個頻段［9］，意味著均衡器的每個濾波器的帶寬都很窄，導(dǎo)致鄰近頻段濾波器之間相互干擾嚴(yán)重［3,10］。降低相互干擾的最直接方法是使用高階FIR濾波器，但是這種情況下濾波器的階數(shù)往往高達(dá)數(shù)千［1,5］。系統(tǒng)的時延與階數(shù)成正比，因而使用高階FIR濾波器會給系統(tǒng)帶來時延高和設(shè)計過程計算量大的問題。

針對這些問題，考慮采用IIR濾波器來構(gòu)建圖示均衡器。IIR濾波器響應(yīng)長度無限長，同時具有非線性相位的特點，因而無法保證穩(wěn)定性［11］。但是，同規(guī)格的IIR濾波器的實現(xiàn)成本要遠(yuǎn)低于FIR濾波器，同時可以節(jié)省更多的空間資源。因此，基于IIR濾波器的圖示均衡器可以應(yīng)用在線性相位要求較低的場景，只要設(shè)計得當(dāng)，也能同時保證IIR濾波器的系統(tǒng)穩(wěn)定性［12-13］。

雙線性變換是設(shè)計圖示均衡器IIR濾波器的最常用方法。然而，雙線性變換會導(dǎo)致系統(tǒng)高頻處的頻率響應(yīng)失真［1,4-5］。為了解決這個問題，通常需修正濾波器高頻處的頻率響應(yīng)［14］，但依然無法保證IIR濾波器的穩(wěn)定性。

為了解決上述問題，本文從優(yōu)化角度出發(fā)，提出一種基于小波分解的圖示均衡器設(shè)計方法。具體地，使用小波分解將信號分解成不同頻段的頻率成分。在各個需要處理的頻段，理想均衡化和實際均衡化之間的絕對誤差作為優(yōu)化問題的目標(biāo)函數(shù)被最小化，同時對優(yōu)化問題添加每個頻率點的誤差約束條件和IIR濾波器穩(wěn)定性約束條件。當(dāng)找到一個優(yōu)化問題的最優(yōu)解時，一個能對該頻段提供有效穩(wěn)定均衡化的IIR濾波器的系數(shù)也將隨之確定。設(shè)計所有頻段對應(yīng)的IIR濾波器后，以并聯(lián)方式連接濾波器，使用各濾波器的輸出重構(gòu)均衡化后的信號。

2 基于IIR濾波器組的均衡器設(shè)計

本文提出的圖示均衡器設(shè)計方法采用分頻段處理方法，通過小波分解將傳輸系統(tǒng)的輸入輸出信號分解為對應(yīng)頻段的分量，使用輸入輸出信號相同頻段的頻率分量設(shè)計出負(fù)責(zé)該頻段均衡化的IIR濾波器。當(dāng)?shù)玫剿蓄l段對應(yīng)的IIR濾波器后，即可組建完整的圖示均衡器。本節(jié)主要講述基于小波分解的頻段劃分和針對單個頻段設(shè)計IIR濾波器的方法。

2.1 基于小波分解的頻帶劃分

小波分解是一種多尺度的信號處理方法，對選定的小波基進(jìn)行壓縮平移，配以適當(dāng)?shù)南禂?shù)復(fù)現(xiàn)原信號，能同時得到信號局部的時域和頻域信息。若需要更小局部的時頻信息，只需對信號做更大尺度的小波分解即可。

國際標(biāo)準(zhǔn)化組織（International Organization for Standardization，ISO）標(biāo)準(zhǔn)根據(jù)人耳聽力敏感程度劃分的10段倍頻頻帶分布與采樣率為44.1 kHz（一般音頻信號采樣率）的信號10層小波分解的各頻帶對比，如表1所示。

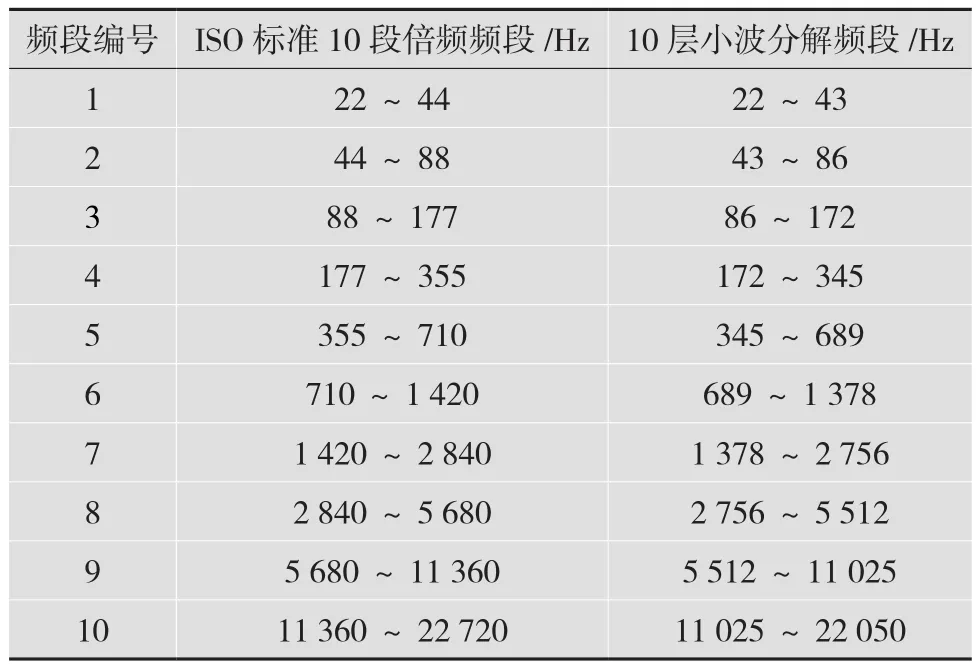
表1 10段倍頻頻帶與10層小波分解的頻段對比

由表1可見，10段倍頻的各頻段與10層小波分解的各頻段相差無幾。因此，可對原系統(tǒng)的輸入輸出信號采用10層小波分解，得到輸入輸出信號對應(yīng)頻段的頻率分量。

2.2 單個頻段的IIR濾波器設(shè)計

針對輸入輸出信號相同頻段的頻率分量，從最優(yōu)化的角度設(shè)計負(fù)責(zé)對應(yīng)頻段均衡化的IIR濾波器。首先，對需要均衡化的信號進(jìn)行10層小波分解，得到對應(yīng)頻段的頻率分量；其次，通過對應(yīng)頻段的IIR濾波器，得到均衡化后的各頻率分量；最后，將所有IIR濾波器的輸出重構(gòu)得到均衡化后的信號。處理流程如圖1所示。

假設(shè)x(n)和y(n)（n=0,1,…,L-1）分別是原系統(tǒng)輸入輸出信號經(jīng)10層小波分解得到的相同頻段的頻率分量，由二者的離散時間傅里葉變換得到原系統(tǒng)在該頻段內(nèi)的頻率響應(yīng)為：

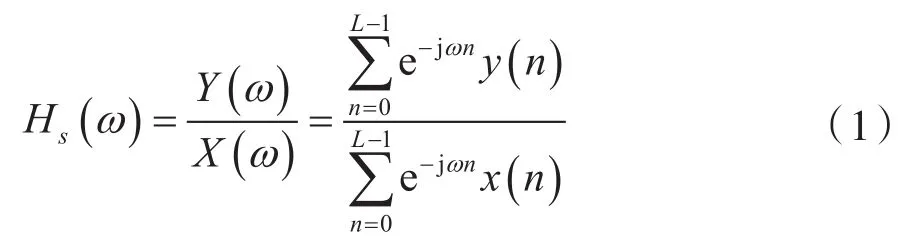
假設(shè)需要設(shè)計的IIR濾波器的頻率響應(yīng)模型為：

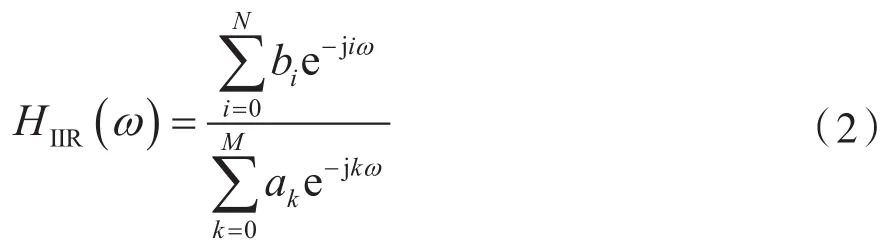
式中，N和M分別是IIR濾波器頻率響應(yīng)中分子和分母多項式的階數(shù)。一般情況下，N和M的取值越大，能得到的均衡化精度越高，但相應(yīng)的計算量也越大。bi(i=0,1,…,N)和ak(k=0,1,…,M)分別是IIR濾波器頻率響應(yīng)分子和分母的系數(shù)。

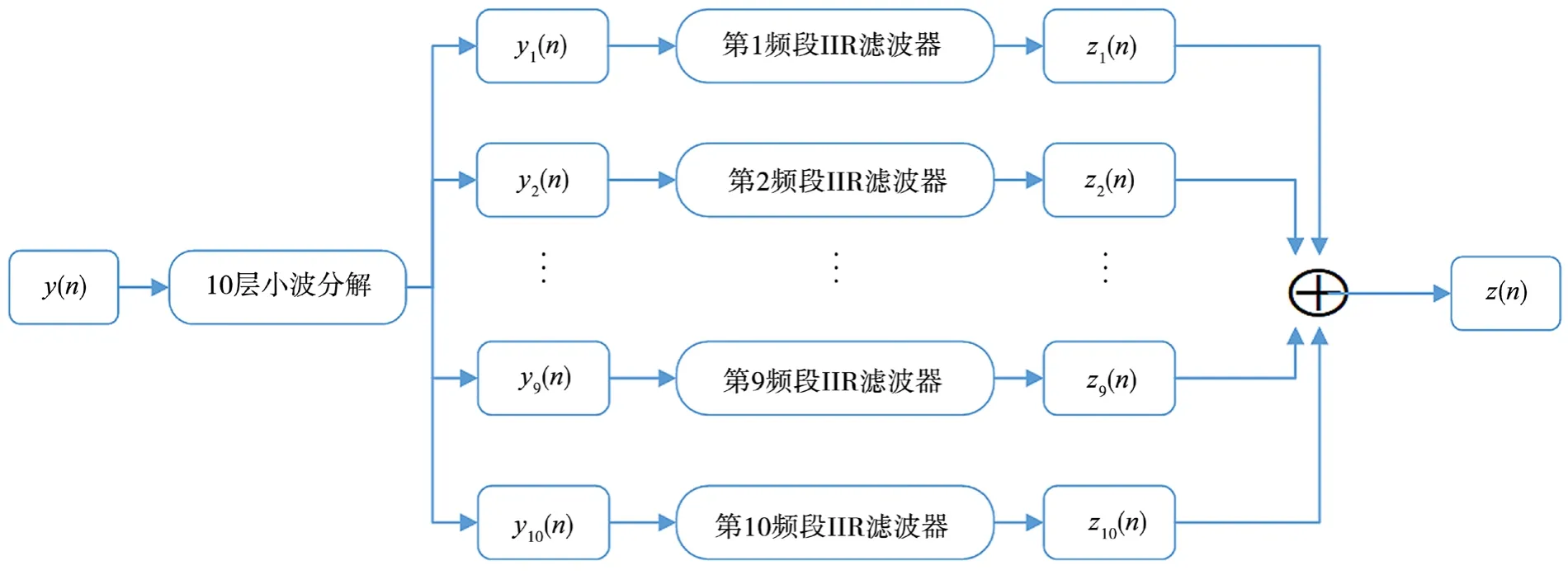
圖1 均衡器處理流程圖

考慮到IIR濾波器的非線性相位特點，為了簡化問題，后文只考慮幅頻響應(yīng)。將IIR濾波器連接在原音頻傳輸系統(tǒng)后，理想情況下能得到如下的均衡化效果：

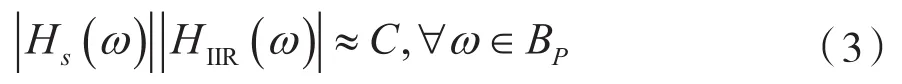
式中，C是圖示均衡器可控的增益，BP為需要此IIR濾波器均衡化的頻段。由于分頻段的工作已通過小波分解完成，此處需要均衡化的頻段為信號分量的全頻帶，即BP為［0,2π］。

對式（3）作變換，可得到：

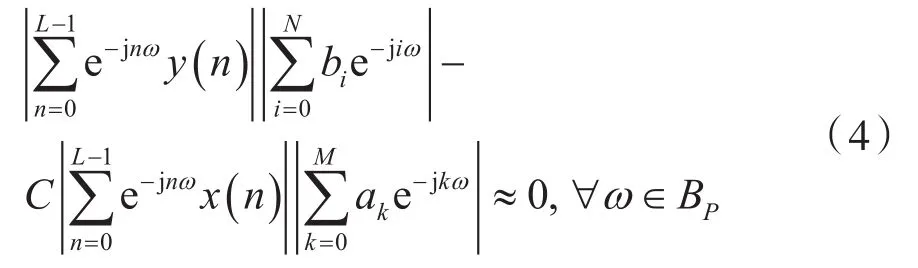
由式（4）出發(fā)，定義頻段內(nèi)單個頻率點處的誤差方程為：

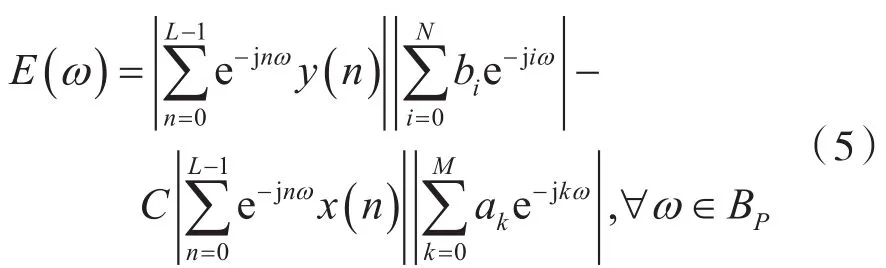
為了簡化誤差方程（5），定義以下向量：

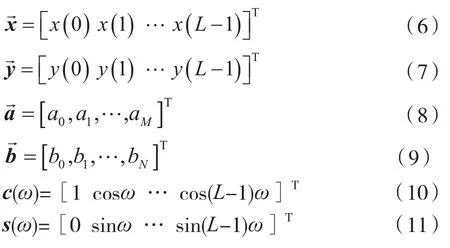
則誤差方程（5）可被簡化為：

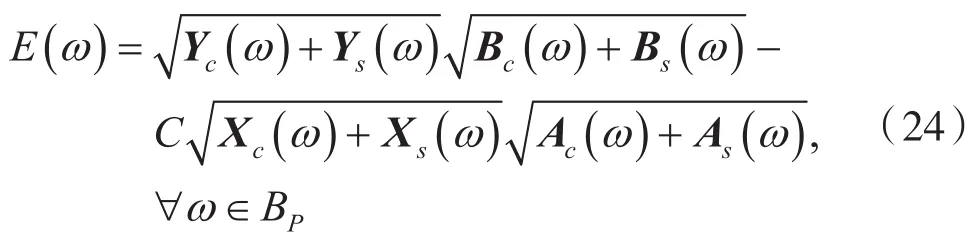
由于需要被最小化的是頻段BP中理想均衡化和實際均衡化間的絕對誤差，即頻段BP中每個頻率點絕對誤差的疊加，因此需要對式（24）的絕對值在頻段BP內(nèi)積分，以此作為優(yōu)化問題的目標(biāo)函數(shù)：

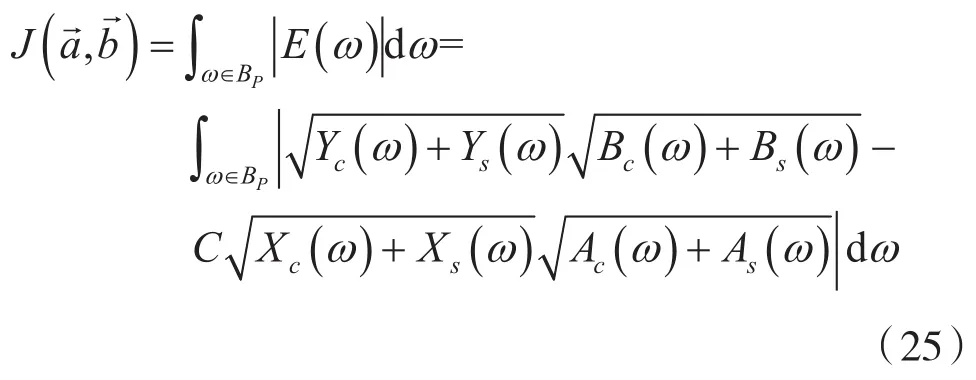
為了防止IIR濾波器在均衡化過程中出現(xiàn)某個頻率點處存在較大誤差的問題，為每個頻率點處的誤差添加約束條件：

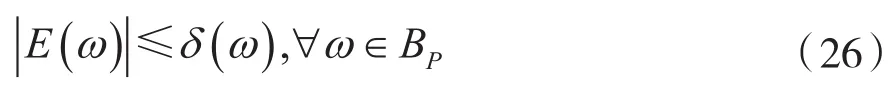
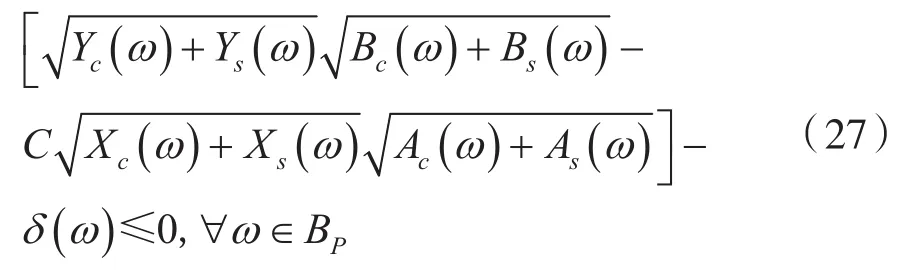
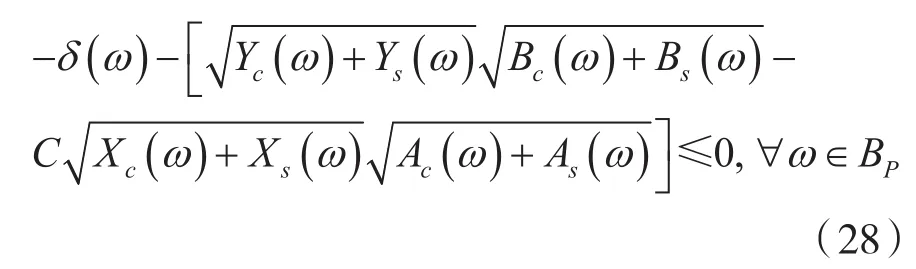
值得注意的是，當(dāng)且僅當(dāng)IIR濾波器傳遞函數(shù)所有分母的根都在單位圓內(nèi)時，IIR濾波器是穩(wěn)定的。文獻(xiàn)［12，15］有此條件的等價條件。因此，為了保證IIR濾波器的穩(wěn)定性，對優(yōu)化問題添加以下穩(wěn)定性約束條件：

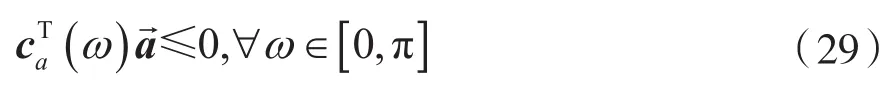
至此，得到完整的優(yōu)化問題：

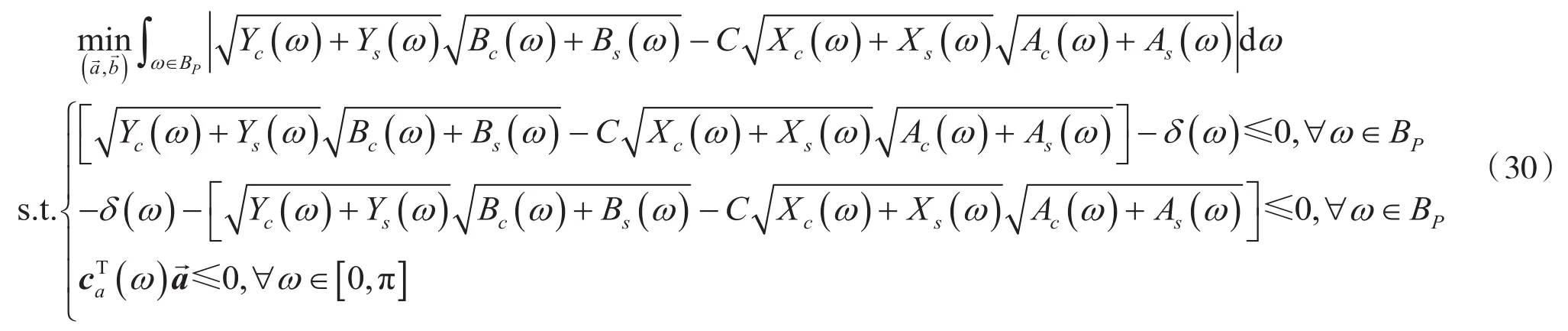
通過調(diào)用遺傳算法，使用合適的算法參數(shù)能解此優(yōu)化問題，得到優(yōu)化問題的最優(yōu)解，即為所設(shè)計IIR濾波器所有系數(shù)的集合。將最優(yōu)解中的元素代回式（2）對應(yīng)的位置，即可得到負(fù)責(zé)此頻段均衡化的IIR濾波器的頻率響應(yīng)。

3 實驗仿真與分析

3.1 實驗仿真

實驗采用從普通音頻文件截取出的片段作為信號，長度為40 000（即L=40 000），采樣率為44.1 kHz（即fs=44 100 Hz），信號中含有［0，22 050］Hz的有效信息，涵蓋人耳聽力范圍。原音頻傳輸系統(tǒng)的輸入信號和輸出信號在時域和頻域中的對比，分別如圖2和圖3所示。

實驗中，IIR濾波器的階數(shù)為50。通過小波分解將音頻分解成10個頻率分量，各分量的頻率范圍如表1所示。對輸入輸出信號對應(yīng)頻段的分量使用上述單個頻段IIR濾波器的設(shè)計方法，設(shè)計出負(fù)責(zé)各個頻段均衡化的IIR濾波器。為了使對比效果明顯，將均衡器各個頻段的增益值設(shè)為1（即C=1），盡可能將均衡器的輸出恢復(fù)到信號經(jīng)過音頻傳輸系統(tǒng)前。

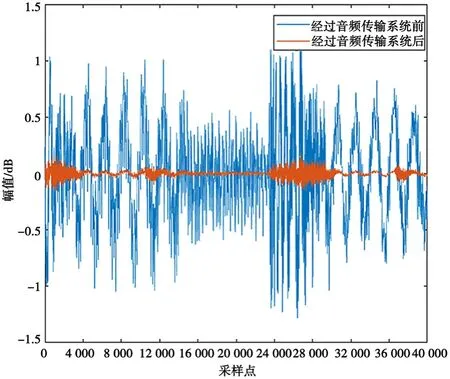
圖2 信號經(jīng)過音頻傳輸系統(tǒng)前后在時域中的對比

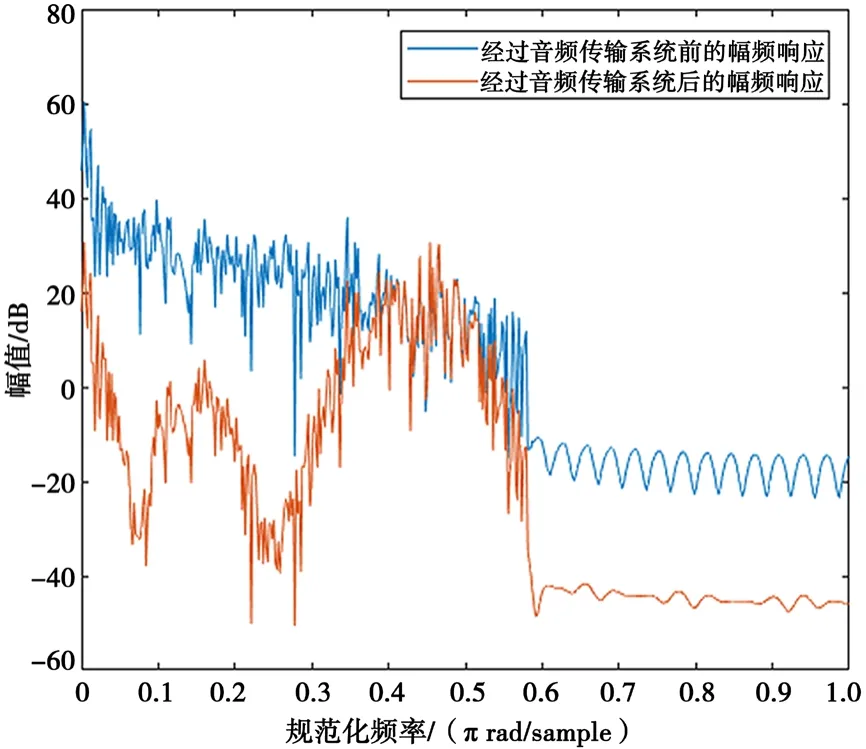
圖3 信號經(jīng)過音頻傳輸系統(tǒng)前后的幅頻響應(yīng)對比

在得到對應(yīng)各個頻段的IIR濾波器后，以并聯(lián)的方式連接各IIR濾波器。需要均衡化的信號先經(jīng)過10重小波分解得到對應(yīng)各IIR濾波器處理頻段的各頻率分量，再由各IIR濾波器實現(xiàn)均衡化，最后由各IIR濾波器的輸出重構(gòu)得到經(jīng)過均衡化的信號。經(jīng)過均衡器處理后的信號與處理前的信號在時域和頻域上的對比，分別如圖4和圖5所示。

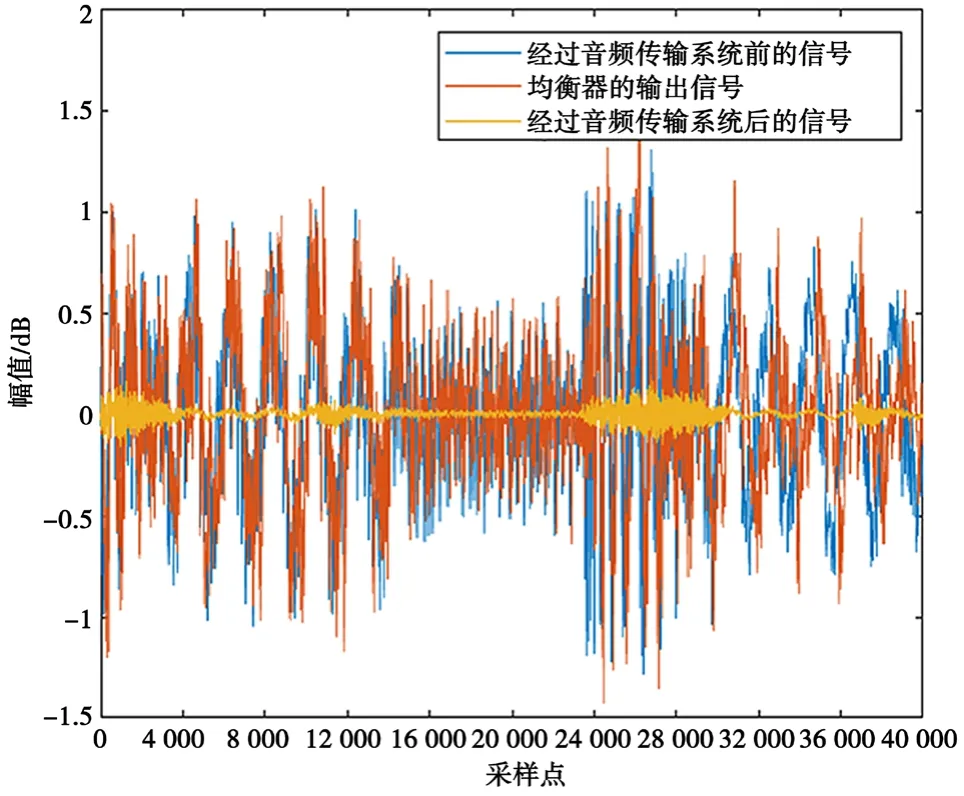
圖4 信號經(jīng)過均衡器處理前后在時域中的對比

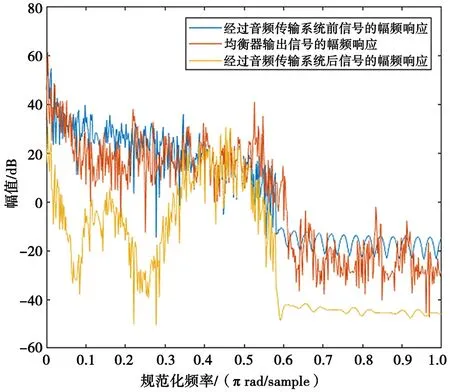
圖5 信號經(jīng)過均衡器處理前后在頻域中的對比

3.2 實驗結(jié)論

從圖4可以看出，經(jīng)過均衡器處理后，均衡器的輸出信號與原信號在時域上相差無幾。從圖5的頻域圖可以看到各個頻率成分在均衡器處理前后的對比，其中原傳輸系統(tǒng)的輸出信號在規(guī)范化頻率［0,0.4π］區(qū)間內(nèi)衰減嚴(yán)重，個別頻率成分的幅值甚至只有-30 dB。經(jīng)過均衡器處理后，衰減嚴(yán)重的頻率分量的幅值也有大約20 dB，和原來的信號相比只有微弱的衰減。此外，均衡器處理帶來的高頻噪聲也只有約-20 dB的幅值，對聲音質(zhì)量的影響很小。

4 結(jié) 語

本文針對一般圖示均衡器時延高、計算量大以及相鄰頻帶間相互干擾的問題，從優(yōu)化問題的角度，提出了一種基于小波分解和IIR濾波器的圖示均衡器設(shè)計方法。相對于一般的圖示均衡器，本文濾波器的階數(shù)低了兩個數(shù)量級，仍然能提供有效的均衡化，同時極大地降低了系統(tǒng)的時延和設(shè)計的計算量，解決了相鄰頻段相互干擾的問題。若要實現(xiàn)更高精度的均衡化，可適當(dāng)加大IIR濾波器的階數(shù)，但系統(tǒng)的延時和設(shè)計的計算量也會相應(yīng)增加。