高考數學試卷與課程標準的一致性研究
張磊 梁芳


摘 要:文章以2019年高考數學全國Ⅰ卷、Ⅱ卷為研究對象,采用韋伯一致性分析模式分析試卷與課程標準一致性。研究表明,2019年高考數學全國Ⅰ卷、Ⅱ卷理科卷與課程標準的一致性和文科卷相同,適應未來高考文理不分科的形勢,且不同地區適合使用相同的高考數學試題,數學卷整體質量較高,但知識廣度與課程標準未達到一致性水平,在試卷編制過程中可以考慮細化與合理分配對各知識模塊的考查。
關鍵詞:高考改革;數學;課程標準;一致性
中圖分類號:G633.6 文獻標志碼:A文章編號:1008-3561(2021)04-0060-04
高考試題與課程標準一致性研究備受關注,但國內研究多以評價試題質量與價值為主。隨著一些地區已經實施高考綜合改革,從試題與課程標準一致性分析的角度來探究試題是否適應高考文理合卷改革政策、能否順應曾經使用不同試卷的地區在未來使用相同試題趨勢這類問題的研究尚未出現。本文對 2019年高考數學全國Ⅰ卷(文科和理科)、高考數學全國Ⅱ卷(文科和理科)進行研究,研究工具選擇韋伯一致性分析模式,剖析在各維度高考數學試題與課程標準能否達到一致性,試從一致性分析的角度探討2019年高考數學全國Ⅰ卷、Ⅱ卷能否為未來高考文理不分科以及使用這兩類試題的部分地區在未來使用相同高考試題的改革政策提供依據。
一、研究設計
1.研究對象
2019年高考數學全國Ⅰ卷(文科和理科)、高考數學全國Ⅱ卷(文科和理科)、《普通高中數學課程標準(實驗)》。
2.研究工具
一致性分析模式是指判斷、分析課程系統各個要素之間吻合程度的理念、程序與方法的總和。目前常見的一致性分析模式有韋伯模式、SEC模式、Achieve模式。我國不乏有學者運用其中某些模式分析試卷與課程標準的一致性,以考查試題價值,如王永強運用韋伯模式分析2015年高考數學試卷與課程標準的一致性,張蕾運用SEC模式分析2019年高考語文試題與課程標準的一致性,陳鵑娟運用Achieve模式分析2018年高考數學試題與課程標準的一致性。
本文的研究工具選擇一致性分析模式的母體——韋伯分析模式。美國CCSSO曾指出,韋伯分析模式在剖析學業評價與課程標準關系的多種方式中是最重要且最具創造性的模式,并證明了其編碼過程的可靠性,在分析試卷知識與技能方面有很高的適用性。
諾曼·韋伯主張要對課程內容標準要進行具體目標的描述,以構建學業評價與課程標準之間的一致性,從而生成形如“金字塔”的課程內容目標的層級體系。金字塔頂端最具概括性地描述了課程內容目標,即內容主題;金字塔的中間部分是單元目標,是內容主題下一級的目標;金字塔底端對應課程內容中最具操作性的目標,即具體目標。目標層級體系為一致性分析評價提供了基礎。諾曼·韋伯從四個不同的維度考查試卷具體內容與課程標準的一致性,依次為“知識種類”“知識廣度”“知識深度”“知識分布的平衡性”。
諾曼·韋伯認為,知識種類的一致性是用來判斷測試題中涉及的學習內容與課程標準中要求考查的學習內容是否一致,當試卷中所涉及課程標準的內容主題的題目數量不少于6,在知識種類這一維度上,該內容主題達一致性。知識廣度的一致性是用來判斷測試題中所考察的內容范圍與課程標準所要求掌握的內容跨度是否一致,當試卷擊中目標數的百分比不小于50%,在知識廣度這一維度上,該主題達一致性。知識深度的一致性是用來判斷測試題中所考查到具體目標的認知深度水平是否符合課標要求的認知深度,符合具體目標認知深度的題目數量百分比不小于50%時,在知識深度這一維度上,該主題達一致性。知識分布的平衡性是用來判斷測試題中考查的知識(具體目標)在課程標準中是否均勻分布,當知識分布平衡性指數不小于0.7,則認為在知識的分布平衡性這一維度上,該主題達一致性。平衡性指數計算公式為:平衡性指數=1-■。(O為該內容主題擊中課標的具體目標總數,Ik為某一具體目標對應的題目總數,H為命中該內容主題的題目總數)
3.對研究對象編碼統計
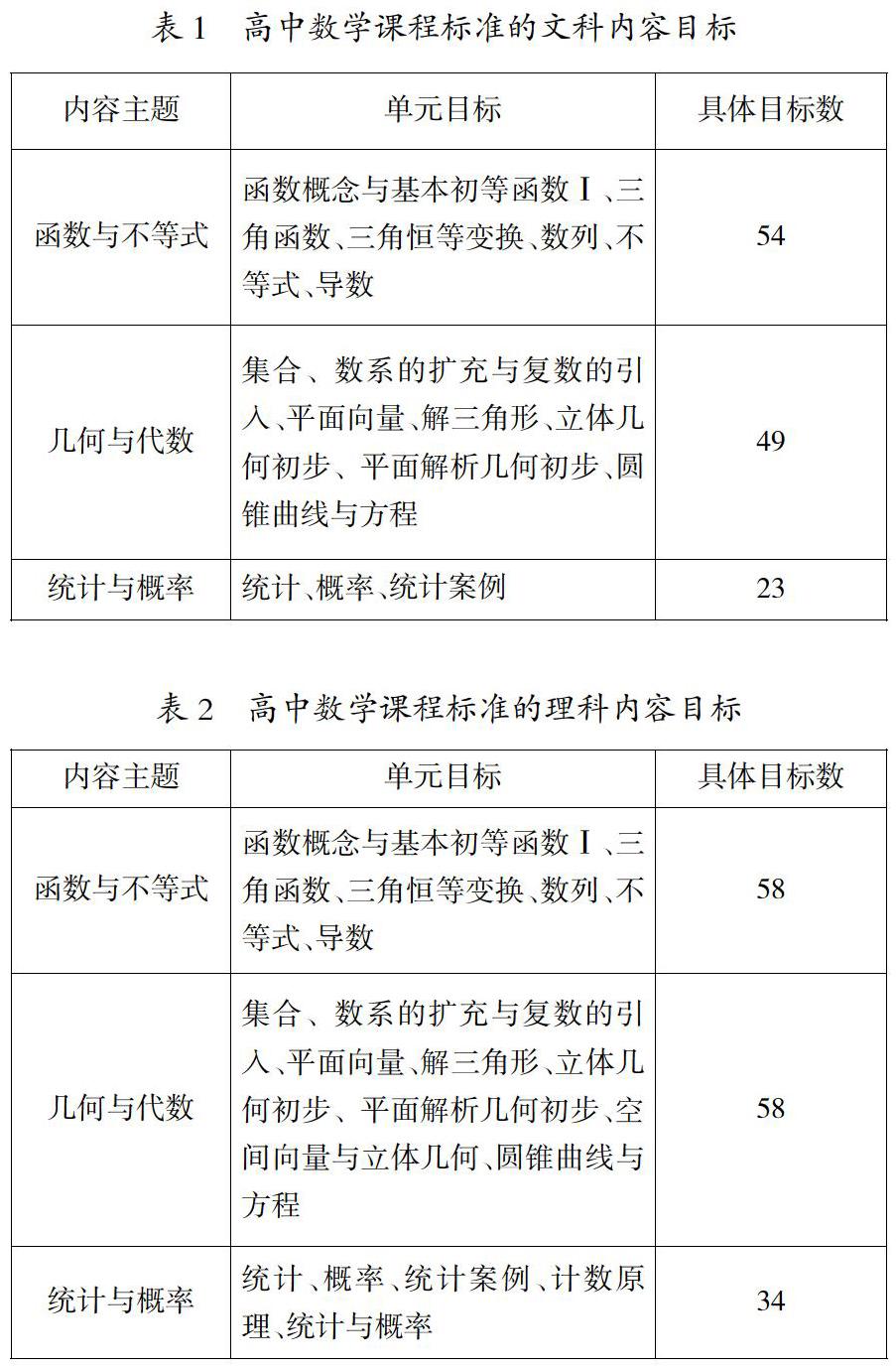
(1)對課程標準編碼統計。我國高中數學涉及三大知識模塊,每個知識模塊分為不同的主題,每個主題下涵蓋的各個知識點,可依次對應為“金字塔”課程內容目標體系的內容主題、單元目標及具體目標。高考數學全國Ⅰ卷、Ⅱ卷中考題的具體考查內容因考生而異,為非主干部分,本文暫不分析“坐標系與參數方程”“不等式選講”這兩個單元。2019數學考試大綱指出知識要求范圍參照高中數學課程標準(實驗版),筆者將課程標準的內容目標對應制為表1、表2。表1與表2有些單元目標名稱雖然相同,但包含的具體目標有差異,有的是知識點存在差異,有的是知識深度水平存在差異。
(2)對高考數學試題編碼統計。編碼過程中,以每道題包含的具體目標為對象,若某題涉及2個具體目標,則記為2個題目。在對數學試題編碼統計過程中,對每個題目的求解過程和步驟都加以分析,與課程標準的具體目標相對照,確定各題目對于相應具體目標考查所達到的深度水平,以及與課程標準要求的深度水平是否相符。
二、研究結果與數據分析
1.全國Ⅰ卷理科卷、文科卷與課程標準一致性分析
由表3~表6可知,在知識種類層面,理科卷與文科卷的一致性結果完全相同,3個內容主題與課程標準均達到一致;在知識廣度層面,理科卷與文科卷的一致性結果相同,3個內容主題與課程標準均未達到一致;在知識深度層面,理科卷與文科卷的一致性結果完全相同,各內容主題與課程標準均達到較高一致性水平;在知識分布平衡性層面,理科卷與文科卷的一致性結果也完全相同,各內容主題與課程標準均達到較高一致性水平。因此,2019年高考數學全國Ⅰ卷理科卷與課程標準的一致性結果完全同于文科卷與課程標準的一致性結果。
2.全國Ⅱ卷理/文科卷與課程標準一致性分析
由表7~表10可知,在知識種類層面,理科卷與文科卷的一致性結果完全相同,3個內容主題與課程標準均達到一致;在知識廣度層面,理科卷與文科卷的一致性結果相同,3個內容主題與課程標準均未達到一致;在知識深度層面,理科卷與文科卷的一致性結果完全相同,各內容主題與課程標準均達較高一致性水平;在知識分布平衡性層面,理科卷與文科卷的一致性結果也完全相同,各內容主題與課程標準均達較高一致性水平。因此,2019年高考數學全國Ⅱ卷理科卷與課程標準的一致性結果完全同于文科卷與課程標準的一致性結果。
三、結論與思考
第一,2019年全國Ⅰ卷、Ⅱ卷文理卷與課程標準一致性結果完全相同,適應未來高考文理不分科的形勢。高考數學試卷由文理兩卷合為一套試卷是高考綜合改革內容之一。雖然文理科卷對個別內容主題下的具體目標要求不同,但2019年高考數學全國Ⅰ卷理科卷與課程標準的一致性結果完全同于文科卷與課程標準的一致性結果,說明文科卷和理科卷對于各個知識種類、知識廣度、知識深度和知識分布平衡性的考查形式與程度存在很大的相似性。全國Ⅱ卷文理卷情況類似,對應課程標準的一致性分析也有相同的結果。因此,對于2019年高考數學全國Ⅰ卷、Ⅱ卷使用地區,高考數學由文理兩卷整合為一套試卷的方案具有一定可行性。
第二,全國Ⅰ卷、Ⅱ卷與課程標準的一致性水平相同,在一定程度上適合不同地區使用相同的高考數學試題。對于全國Ⅰ卷、Ⅱ卷與課程標準的一致性分析結果呈現相同的一致性分布:在知識種類這一層面,都達到了一致性水平;在知識廣度這一層面,所有試卷均未達一致;在知識深度與知識分布平衡性這兩個層面,所有試卷與課程標準都達到了較高的一致性。通過對當前全國Ⅰ卷、Ⅱ卷與課程標準的一致性分析可知,未來可以在一定程度上在不同地區使用相同的高考數學試題。
第三,2019年全國Ⅰ卷、Ⅱ卷數學卷整體質量較高,但知識廣度與課程標準未達到一致性水平,在試卷編制過程中可以考慮更加細化與合理地分配對于各知識模塊內容的考查。根據全國Ⅰ卷、Ⅱ卷的文理卷與課程標準的一致性分析結果可知,在知識種類層面,各內容主題均達到一致性,因此試卷所考查的知識范圍相對于課程標準較為適宜。知識深度與知識分布平衡性方面三個內容主題也都達到較高的一致性水平,試卷整體質量較高。然而,在知識廣度層面,各高考數學試卷的所有內容主題與課程標準均未達到一致性水平,這可能是由于試卷編制可能存在某些題型分數占比偏高或題目類型相對單一的問題。因此,對于題目分數分配與試題類型尚存在改進的空間,對于各知識模塊內容的考查可以更加細化與合理。以全國Ⅰ卷、Ⅱ卷為例,選擇與填空題共計16題,每題5分,共計80分;解答題共計6題,必考題含5題,每題12分,選考題有1題,每題10分,共計70分。對于各題目分數分配,在難度適當的前提下,選填部分可適當減少每題分數而相應增加題目總數,解答題部分可在某些題目適量增加設問,也可考慮在此基礎上適應性地調整客觀題與主觀題的分數分配比例,使對學生在知識廣度層面的考查達到更高的效度;在試題類型方面,可考慮增加多選題等其他類型題目,在一題中考查更多的知識模塊內容,從而在知識廣度層面與課程標準達到更高的一致性水平,提高試卷質量。
參考文獻:
[1]Norman L W. Alignment of Science and Mathematics Standards and Assessments in Four States[M].Washington D C:Council of Chief State School Officers,1999.
[2]王永強,韓洪芹.高中數學課程標準與數學高考試卷的一致性分析——基于韋伯分析模式的研究[J].教學研究,2016(05).
[3]張蕾,劉聰.2019年全國高考語文試題與課程標準的一致性研究:基于SEC模式[J].教育測量與評價,2019(12).
[4]陳鵑娟,周瑩.基于Achieve模式的2018年全國高考數學試題與最新版課程標準一致性研究[J].教育測量與評價,2019(06).
[5]Norman L W. Criteria for alignment of expectations and assessments in mathematics and science education[M].National Institute for Science Education University of Wisconsin-Madison,1997.
[6]Porter, A.C. and Smithson, J.L. Standards-based reform in The states Chicago: National Society for the study of Education[M]. Chicago: University of Chicago Press,2001.

