基于極點配置的PMSM電流環PI控制器設計
許文波 焦瑋瑋 潘 龍
北京精密機電控制設備研究所,北京 100076
0 引言
在運載火箭/彈道導彈各分系統中,伺服機構是運載火箭/彈道導彈的關鍵組成部分。永磁同步電機(PMSM)具有結構簡單、體積小、重量輕、損耗小等優點,機電伺服機構組成簡單,具有可靠性高、維護保養要求低,測試、使用方便等特點,因此在航天型號研制中得到了廣泛應用[1-3]。基于PMSM的伺服控制系統是一個包含位置、轉速、電流環的多閉環系統。其中,作為最內環的電流環決定著電流的跟蹤性能,響應的快速性,直接影響PMSM的輸出電磁轉矩,進而影響機電伺服機構的性能。
在PMSM電流環控制方式上,近年來許多先進的電流控制方法不斷被提出,如非線性預測控制、反推控制、模糊PI控制、神經網絡控制、滑模控制等[4-8]。工程中PMSM驅動系統多采用結構簡單、易于實現、性能良好、對控制對象參數變化不敏感的PI控制器。因此,對于PMSM驅動系統比例積分(PI)控制器參數設計和整定方法的研究極具工程價值。
PI控制器的參數整定方法通常分為2類:1)基于實驗的方法,如Ziegler-Nichols整定法;2)通過對被控對象進行建模,然后通過測量或辨識模型參數計算得到控制器參數。1984年Astrom和Hagglund首次提出了基于幅值裕度和相角裕度的PID參數自整定方法[9]。文獻[10]旨在通過幅值裕度和相位裕度獲得最佳閉環特性的PID參數。文獻[11]基于PMSM調速系統的頻域模型,推導出了電流環PI控制器參數Kp和Ki的解析計算式,通過這些解析式,實現設定的期望開環截止頻率和相位裕度,但并未考慮系統的零極點分布及對系統性能的影響進行分析。文獻[12]研究了基于主導極點和相位裕度的PID整定算法,通過在控制器的零點配置主導極點的方式得到PID整定式,但未考慮系統零點的影響。文獻[13]未考慮系統零點對階躍響應瞬態分量的影響。文獻[14]提出了通過對PI控制參數取值的約束進行零極點抵消的方法,但控制參數的取值受到了限制。
本文通過零極點分布對系統性能的影響分析,推導了零極點抵消的條件,確定系統極點的形式,再根據期望的系統帶寬及超調確定期望極點并進行PI參數設計。通過仿真分析驗證了本文提出方法的正確性,具有較強的工程應用參考價值。
1 預備知識
考慮SISO系統,對給定線性定常系統的狀態空間描述為
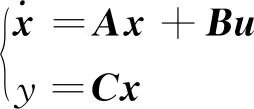
(1)
其中,A為n×n常陣,B為n維列向量,C為n維行向量;u為對系統施加的控制,若u取為系統狀態x的線性函數和一個輸入向量v,可表示為
u=-Kx+v
(2)
式中,K=[K1,K2,…,Kn]為n維行向量。
代入式(1),得到閉環系統的狀態方程為
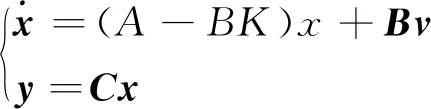
(3)
通過(1)、(3)兩式比較,所謂極點配置,就是通過選擇反饋矩陣K,將閉環系統的極點恰好配置在根平面上所期望的位置,以獲得所希望的動態特性。而控制系統的性能主要取決于系統極點在根平面上的分布。因此,在系統設計中,通常是根據對系統的品質要求,規定閉環系統極點應有的分布情況。
由現代控制理論可知,線性定常系統(1)可通過狀態變量反饋來任意配置其全部極點的充要條件是該系統為完全能控的。因此,對于一個完全能控的線性系統的極點配置問題,實際上轉化為求解狀態反饋增益矩陣K。
引入狀態反饋后閉環系統(3)的特征方程可以寫成
|sI-A+BK|=sn+α1sn-1+…+αn=0
(4)
設給定的閉環系統的n個所期望的極點是(λ1,λ2,…,λn),則有
(5)
分別令αi=βi(i=1,2,…,n)則可求解狀態反饋增益矩陣K。
2 PMSM電流環數學模型
2.1. PMSM的數學模型
在分析永磁同步電機的數學模型時,常做如下假設:
1)忽略磁路飽和,不計鐵心中的渦流和磁滯損耗;
2)三相繞組對稱,在空間上互差120°電角度;
3)轉子上沒有阻尼繞組,永磁體也沒有阻尼作用;
4)氣隙磁場呈正弦分布,忽略高次諧波的影響。
在d-q旋轉坐標系下,Ld=Lq=L,采用id=0控制,PMSM的電壓方程、轉矩方程以及機械運動方程可分別表示如下:
(6)
(7)
(8)
式中,ud,uq為d、q軸電壓;iq為q軸電流;ψf為永磁體磁鏈;R,L為定子繞組電阻和電感;Ke為電機的反電動勢常數;ω為電機的機械角速度,Kt為轉矩常數;J為轉動慣量;b為粘滯摩擦系數;TL為負載轉矩。
2.2 PMSM電流環PI控制
作為數字控制系統內環的電流環,主要實現d、q軸電流的快速跟隨及電流限幅,其采樣頻率遠高于速度環采樣頻率,具有較高的控制環路帶寬,在本文中設逆變器的電壓增益為Kinv,忽略濾波器及逆變器動態特性對電機轉速特性的影響,電流和速度控制器均采用經典PI結構,即
(9)
綜合式(6)~(9),可以得到PMSM電流環控制系統框圖如圖1所示。
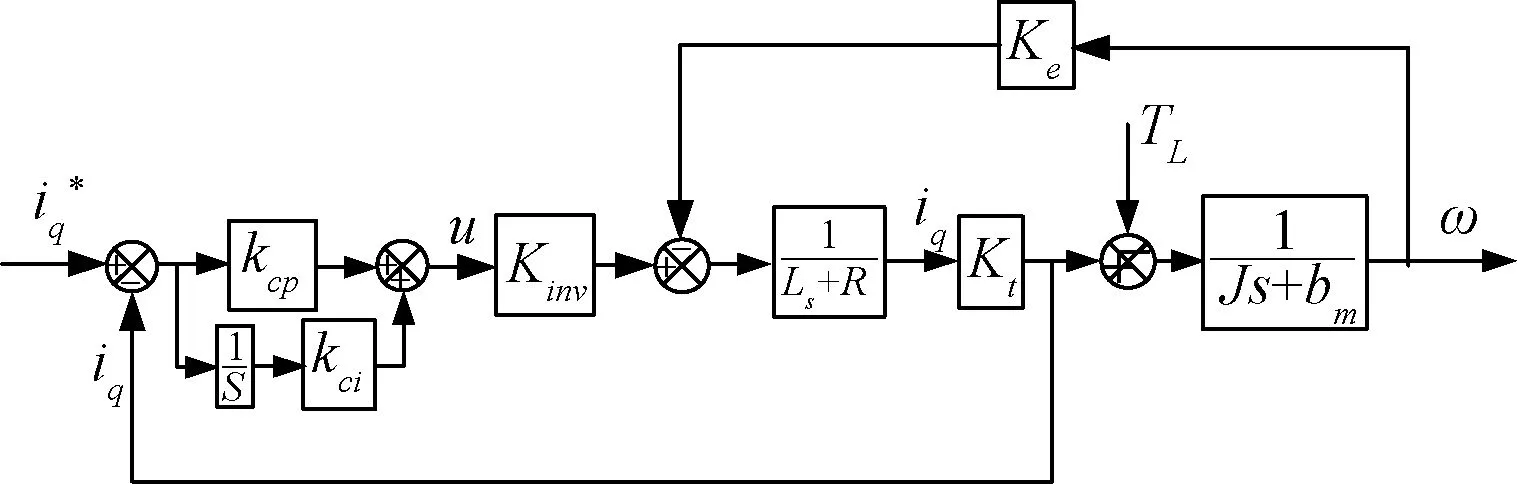
圖1 PMSM電流環PI控制框圖
2.3 PMSM電流環PI控制系統狀態空間描述
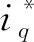
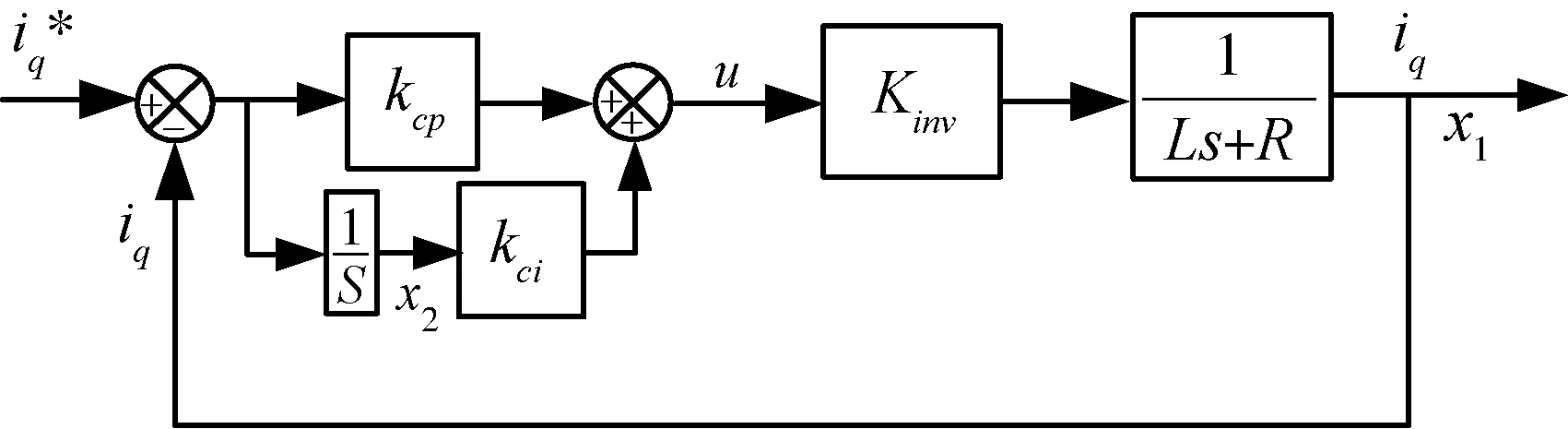
圖2 忽略反電動勢PMSM電流環PI控制框圖
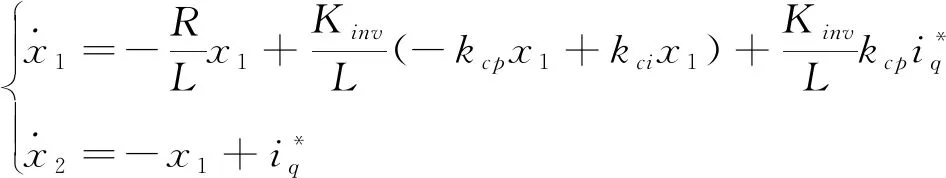
iq=x1
(10)
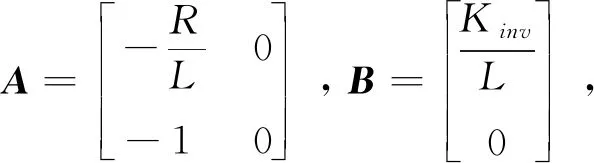
寫成矩陣形式
(11)
3 基于極點配置的PI控制參數設計
3.1 電流環能控性分析
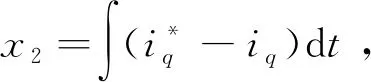
由式(10)~(11)可知,通過狀態變量的選取,PMSM電流環PI控制系統可以轉換為全狀態反饋控制問題。系統(10)可通過狀態變量反饋來任意配置其全部極點的充要條件是該系統為完全能控的,即
rank[B?AB]=2
(12)
對于本文考慮的SISO系統,式(12)等價于
det([B?AB])≠0
(13)
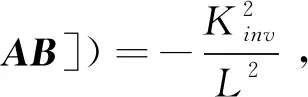
3.2 電流環的零極點分析
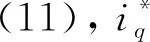
(14)
其中,I為單位矩陣,將矩陣代入并經化簡,其零、極點特征方程分別為
kcps+kci=0
(15)
Ls2+(R+Kinvkcp)s+Kinvkci=0
(16)
對比式(9)和(15),該零點正是由PI控制器引入的電流環開環零點,進而成為閉環零點,該零點為一負實零點,如下
(17)
電流環閉環極點為
(18)
由式(18)可知,PI控制器的比例增益kcp決定了電流環極點與虛軸的距離,即決定了電流環的快速性;積分增益kci決定了電流環極點的虛部和閉環零點,極點虛部影響系統的超調和振蕩;電流環閉環零點的存在會縮短電流環的調節時間和增大其超調。
電機控制中,為了獲得良好的快速性,電流環極點與虛軸應有一定距離,kcp不宜太小,也允許電流環存在一定的超調。但需避免電流環超調引起的大電流沖擊電力電子器件,系統的阻尼比仍然不能太小,kci不能太大。
先討論電流環控制系統具有一對共軛復數極點的情況:
假設存在一組控制參數kcp,kci,使得電流環控制系統存在一對共軛復數極點,則
(R+Kinvkcp)2<4LKinvkci
(19)
(20)
再假設該系統的一對極點為pc1,2=-a±jb,其中a正實數,b為非負實數,代入特征方程式(15)可得其零點如下
(21)
對具體電機而言,R和L確定,故為獲得快速的調節過程,電流環控制系統的極點距離虛軸不能太近,通常存在a>R/L。由于閉環零點的存在,為了有效抑制電流環超調,系統阻尼比不能太小,當系統阻尼比大于0.707時有a>b,此時有
(22)
式(22)表明,閉環零、極點與虛軸距離之比小于2,因此閉環零點對系統性能的影響不能忽略;同時一對共軛復數極點又無法與閉環零點抵消。
由自動控制原理可知,此時電流環將存在較大超調振蕩。
再討論電流環控制系統具有兩個負實極點的情況:
設該系統的一對極點為pc1=-a和pc2=-b,其中a、b均為正實數,且a>b,則下式成立
(23)
比較系統零、極點之間的關系有
(24)
由式(24)可知
1)當b>R/L時,閉環零點位于兩極點右側;
2)當b=R/L時,閉環零點與一極點重合;
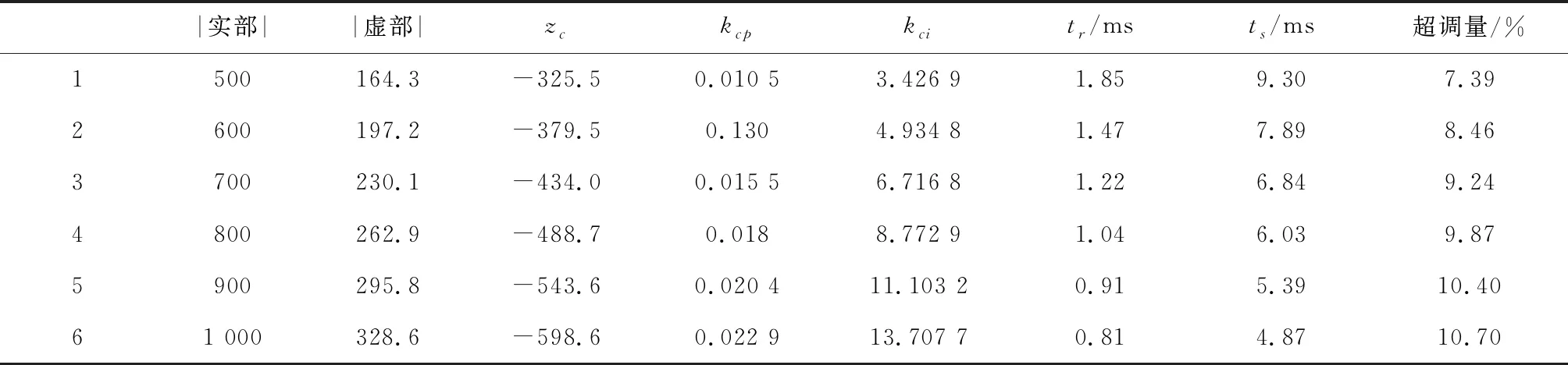
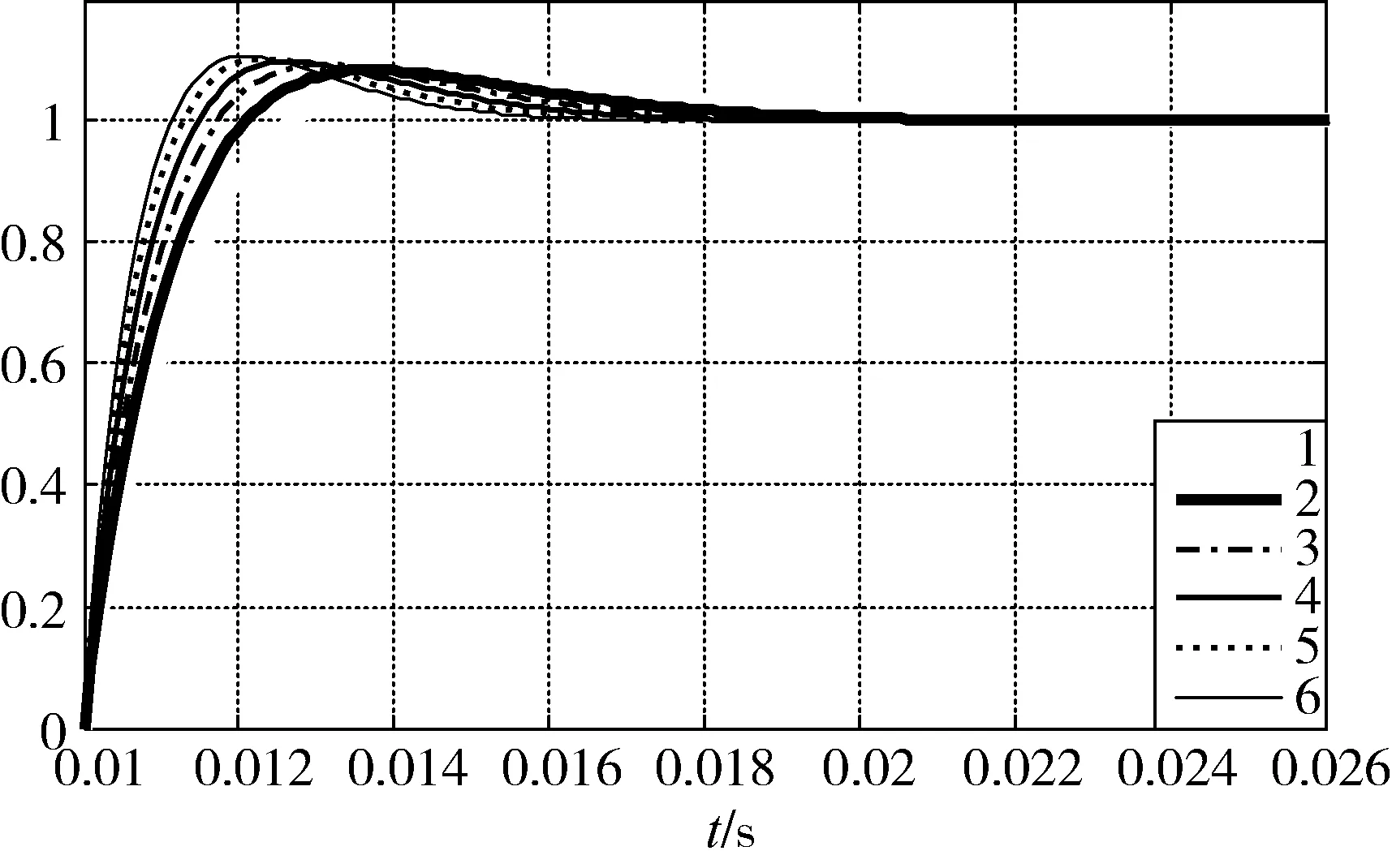
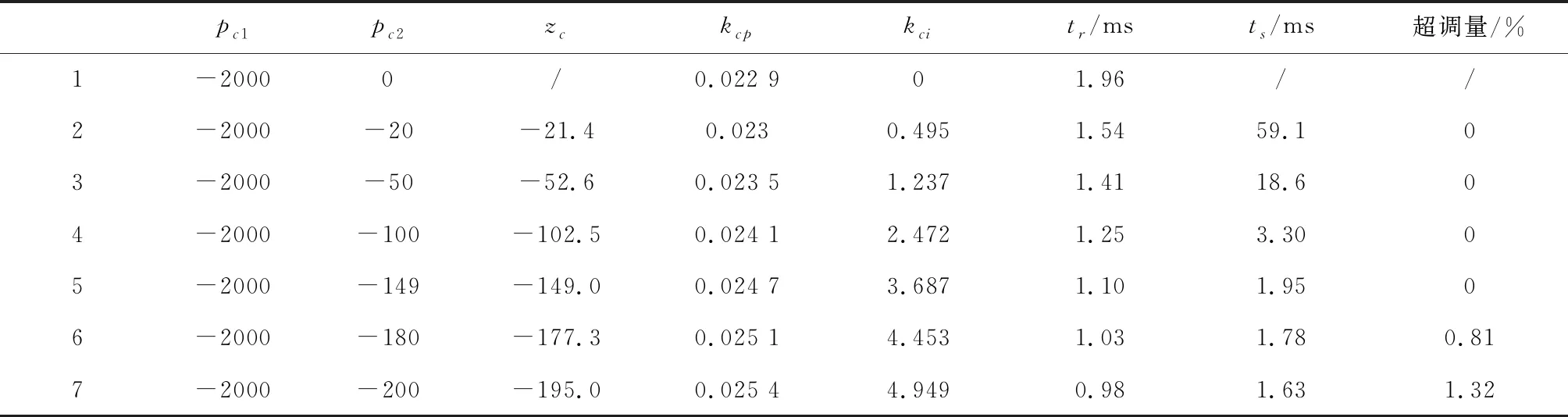
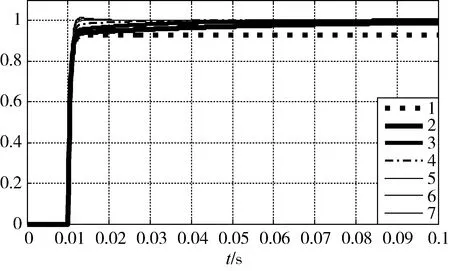
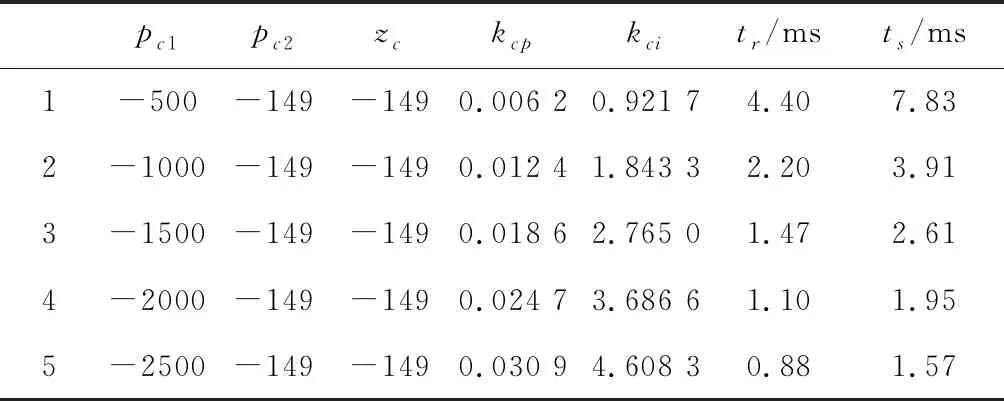
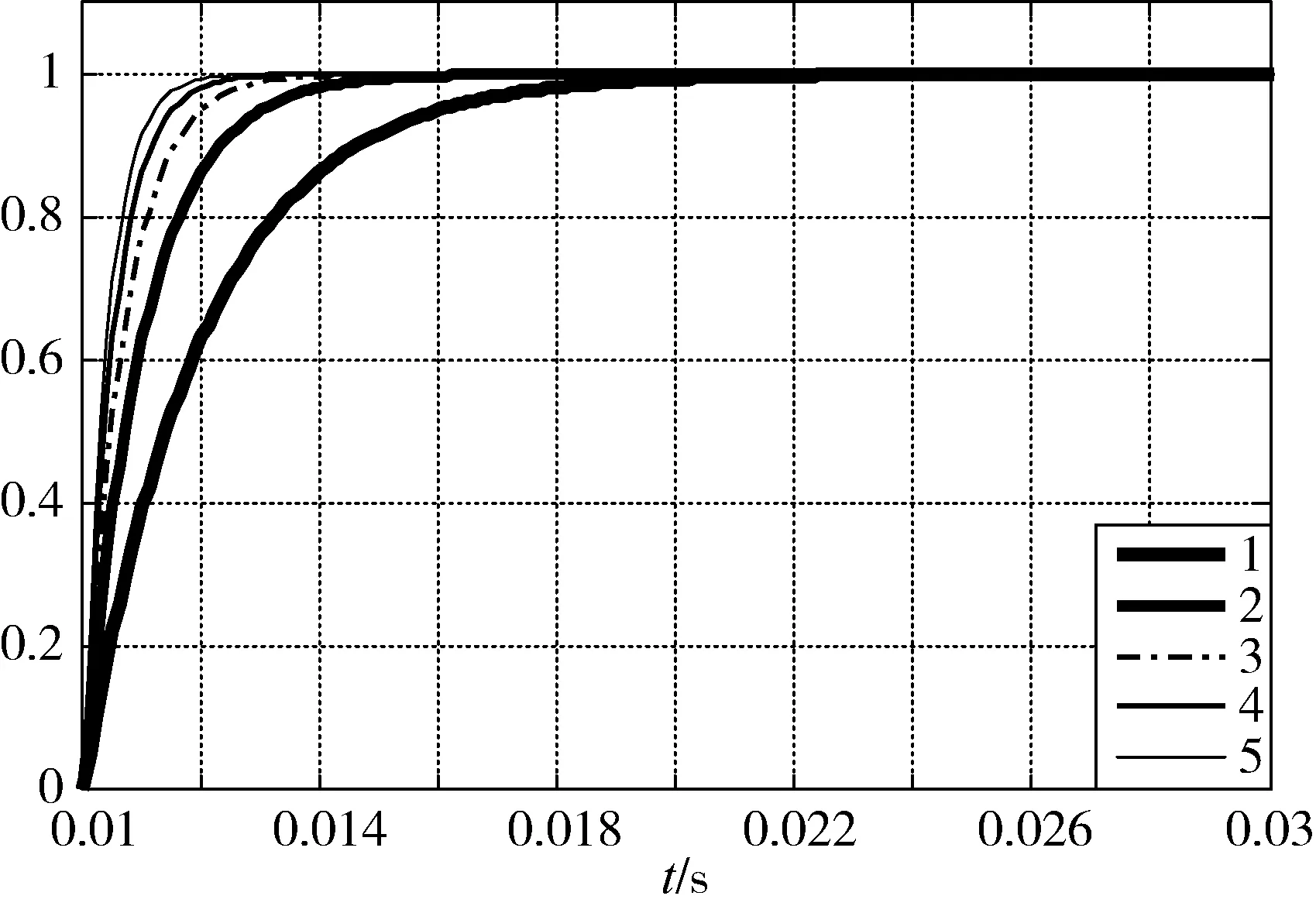
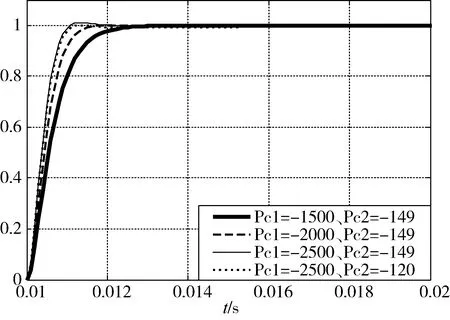
3)當b 在理想情況下,不考慮SVPWM電源逆變器控制周期、開關延遲、死區時間、濾波網絡和數字控制延時等,根據零、極點的相對位置,當b≤R/L時,電流環無超調。但實際工程應用時,系統存在開關延遲等非理想因素,可適當將b值取得小一些,但b值太小可能會導致電流環跟蹤存在靜差,或跟蹤速度過慢。 進一步分析式(24)有 (25) 若b≈R/L或a?b,為了保證系統的快速性有a?R/L,則下式成立 zc-pc2≈0 (26) 式(26)表明,通過對電流環極點配置,基本可以抵消閉環零點對電流環性能的影響,電流環的性能取決于極點pc1=-a,在研究速度環時,若把電流環等效為一階慣性環節,其閉環帶寬ωcb=a(rad/s)。 逆變器工作時易產生復雜的開關諧波,為了避免引入干擾,希望開關諧波處于系統的高頻段,即開關頻率應大于10ωcb,即 (27) 式中Tinv為逆變器控制周期。 (28) 則 (29) 實際系統中存在多種非理想環節,在進行電流環極點配置時對a的取值可保守一些,以保證電流環的穩定裕量。 綜上,電流環極點配置的原則和步驟為 1)根據期望的速度環閉環帶寬及逆變器的控制周期確定其遠極點,保留一定的穩定裕量,保證電流環不產生振蕩; 2)選擇和調整其近極點,使電流環的跟蹤速度、跟蹤靜差和超調量滿足要求; 3)根據期望極點,按式(23)計算kcp和kci。 利用Matlab中的SIMULINK模塊進行仿真,仿真使用如圖2所示的PMSM電流環PI控制系統。 電機參數按某型PMSM實驗數據進行選取,具體如下: L=0.002H,R=0.292Ω,J=1.2×10-4kg·m2,bm=0.000 015Nm·s,Kt=0.225Nm/A,Ke=0.149V·rad/s;取逆變器放大系數Kinv=158.4V。 其電氣時間常數為 Te=L/R=0.0067=1/149(ms) (30) 首先按一對共軛復極點配置進行仿真驗證,為了驗證系統具有較大的超調量,在極點配置時取極點的阻尼比ζ=0.95,由表1可以看出,在共軛復極點配置策略下,系統存在一個較大極點,kci取值較大,盡管所配置極點阻尼比很大,但由于系統零點無法與極點進行抵消,因此系統存在較大的超調,調節時間較長。圖3為共軛復極點配置策略下的系統階躍響應曲線。 表1 共軛復極點配置策略下系統參數 圖3 共軛復極點配置策略下系統階躍響應曲線 表2和圖4分別為固定遠極點配置策略下系統參數和階躍響應曲線,將系統遠極點取固定值pc1=-a=-2000;與表1結果相比,得到的kci參數均較小,隨著近極點遠離虛軸,kci取值逐步增大,系統零點也遠離虛軸,系統響應加快;在此策略下系統的近極點pc2和零點zc基本重合,當近極點pc2=-R/L=-149時,與系統零點重合,系統達到臨界超調狀態;當極點與虛軸太近時,積分效果不明顯,系統的調節時間很長。 表2 固定遠極點配置策略下系統參數 圖4 固定遠極點配置策略下系統階躍響應曲線 表3 和圖5為固定近極點配置策略下系統參數和階躍響應曲線,隨著極點遠離虛軸,kcp,kci都逐漸增大,系統響應加快,因近極點pc2=-R/L=-149,系統均未出現超調,但當電流環達到一定帶寬后,再繼續增大對系統快速性影響不大,反而會因電源逆變器控制周期、死區等非理想環節,降低電流環的穩定裕量。 表3 固定近極點配置策略下系統參數 圖5 固定近極點配置策略下系統階躍響應曲線 圖6 為用一階慣性環節代替非理想環節的電流環階躍響應曲線,由于非理想環節的存在導致pc1=-2500時,電流環出現超調,通過調整任一極點均可避免系統超調,但相比之下,調整pc2能夠有效消除系統的超調,且對系統的快速性影響不大。 圖6 考慮非理想環節的系統階躍響應曲線 綜上,仿真結果表明:當電流環配置一對共軛復極點時,將產生較大超調;驗證了本文提出的通過零極點抵消的極點配置方法能夠有效抑制或消除系統的超調,提高系統的穩定性。 針對PMSM電流環PI控制,提出了一種極點配置方法,通過分析推導了系統零極點抵消的條件,并根據期望極點確定PI控制參數,仿真結果驗證了所提出整定算法可行有效。該方法簡潔明了、算法物理意義明確,具有較強的工程應用和推廣價值。3.3 電流環的極點配置及PI參數設計
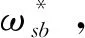
4 仿真結果
5 結語

