基于小波去噪的ARIMA-LSTM混合模型及對股票價格指數的預測

婁磊，劉璐，劉先俊，施三支

（長春理工大學 理學院，長春 130022）

ARIMA模型由Box與Jenkins于上世紀七十年代提出[1]，廣泛應用于時間序列的預測，并取得了非常好的效果，因此ARIMA模型也被應用在了股票價格指數的預測上。我國經濟學者陳守東、孟慶順、楊興武等人[2]最早于1998年對中國股票市場的有效性進行檢驗分析，并且應用ARIMA模型驗證了上海、深圳股市的同步性，得出我國股票市場還在發展初期，但他們并沒有對股指進行預測。趙志峰[3]于2003年建立ARIMA模型對我國股票價格指數進行預測，并得出干預模型更好的結果，同時也說明了我國市場是一個政策市場。吳玉霞、溫欣[4]在2016年使用“華泰證券”250期的股票收盤價格作為時間序列分析數據，建立ARIMA模型進行實證檢驗，證明了ARIMA模型在短期動態、靜態預測效果好的特點。

早在二十世紀八、九十年代，許多專家學者開始探討循環神經網絡（RNN），并在二十一世紀將其發展成為深度學習算法之一[5]。由于循環神經網絡無法克服梯度消失和梯度爆炸的缺點，Sepp Hochreiter和 Jurgen Schmidhuber于 1997年提出長短期記憶神經網絡（LSTM）來進行長期預測[6]，主要應用領域是語言模型以及文本生成[7-8]、機器翻譯[9-11]、語音識別[12]、圖像生成等。近十多年隨著機器學習的興起，越來越多的學者用神經網絡對股票價格指數進行預測。林春燕、朱東華[13]于2006年利用了Elman神經網絡對股票價格進行預測，并得到了不錯的效果。隨著時間的推移，我國經濟學家開始使用混合模型進行預測。回旋[14]認為股票市場是一個極其復雜的非線性動力學系統，具有高噪聲、非線性和投資者的盲目任意性等因素，造成其價格的波動往往表現出較強的非線性特征，針對這些問題提出了TS模糊規則與神經網絡結合的模型，并對綠景地產等進行實證檢驗。彭燕、劉宇紅[15]結合LSTM神經網絡的特點，先對數據進行插值、小波去噪預處理，再通過調整LSTM層數與隱藏神經元的個數提高預測精準度。于水玲[16]于2018年基于深度學習對金融市場的波動率進行了預測，也取得了不錯的效果。

綜上，對股票價格指數的研究大致可以分為三個階段。第一階段使用ARIMA模型對股票價格指數進行預測；第二階段使用神經網絡對股票價格指數進行預測；第三階段使用各種混合模型對股票價格指數進行預測，旨在不斷提高預測精準度。

為了提高預測精度，提出了使用小波去噪后的數據，采用ARIMA-LSTM混合模型的方法進行預測。采集2009年7月至2018年12月共計114個月上證指數每日收盤價格，經小波去噪法預處理后做為訓練集，對2019年1月至2019年6月共計6個月的上證指數進行實證預測，預測結果與單獨使用ARIMA模型與LSTM神經網絡模型相比，ARIMA-LSTM混合模型效果較好。

1 相關的模型理論簡介

1.1 ARIMA模型

假設有時間序列輸入為x1,x2,…,xT,{εt}是高斯白噪聲，則：

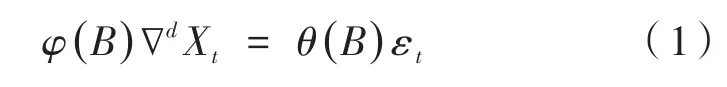
為求和自回歸滑動平均模型，記為ARIMA(p,d,q)，其中d為差分的階數，p，q為自回歸與滑動平均的階數，且：

式中，B表示后移算子。根據平穩性的要求，多項式φ(z)和θ(z)的根在單位圓外，即|z|>1。

1.2 LSTM模型

當序列長度很大時，RNN模型會發生爆炸/消失梯度，因此很難捕獲序列數據中的長期相關性，為了克服RNN模型缺點，Sepp Hochreiter和Jurgen Schmidhuber提出了 LSTM模型[6]。

假設有時間序列輸入為x1,x2,…,xT，LSTM模型有如下形式：

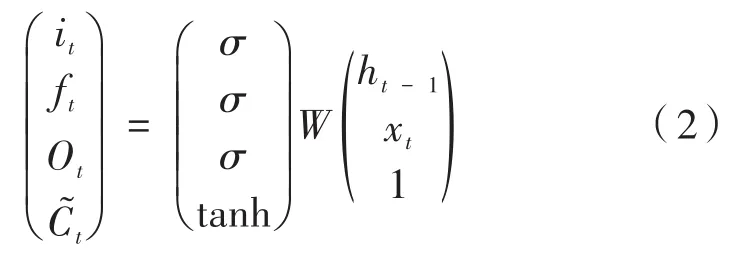
其中，W是具有適當維數的大權重矩陣，且：

根據LSTM的結構，單元狀態向量Ct表示攜帶序列信息，遺忘門ft決定Ct-1的值在時間t內保留多少，輸入門it控制單元狀態的更新量，輸出門Ot給出Ct向ht顯示多少，b表示偏差權重向量（例如，bi是輸入門的偏差權重向量），σ為sigmoid或relu函數。LSTM具有類似RNN的鏈式結構，如圖1所示，但是與RNN相比較而言，LSTM的結構相對復雜。

圖1 LSTM結構圖

LSTM包含一個特殊的單元，即遞歸隱藏層中的內存塊。這些內存塊包含具有自連接的內存單元，這些內存單元存儲網絡的時間狀態，此外還包含特殊乘法單元“門”，用于控制信息流。每個內存塊都包含一個輸入門和一個輸出門和遺忘門。

假設包含一個LSTM層的三層長短期記憶網絡輸入向量序列為x=(x1,…,xT)，輸出向量序列h=(h1,…,hT)，則LSTM的向前傳播流程可以用如下具體表示：

其中，t=1,…,T。內模塊輸出ht受到四個輸入的加權影響，并且在學習時還要將拼接的權重W進行分割，即：

1.3 ARIMA-LSTM混合模型

假設有時間序列輸入為x1,x2,…,xT,ARIMALSTM混合模型有如下形式：

ARIMA模型對數據線性部分有很好的擬合效果，而LSTM模型對非線性數據有好的預測效果，而上證指數的收盤價也同時具有線性和非線性成分，基于誤差的補償思想給出ARIMA-LSTM混合模型可對上證指數進行預測.由于股票數據的高波動性，因此在預測前對數據進行小波去噪預處理，來剔除異常數據可以提高預測準確率，這里用平均絕對誤差（MAE）和均方根誤差（RMSE）：

作為評價模型預測效果，預測步驟如下：第一步使用小波去噪法對數據進行預處理；第二步建立ARIMA預測模型；第三步進行模型檢驗；第四步使用ARIMA模型預測；第五步建立LSTM模型預測殘差序列；第六步加和得到ARIMA-LSTM混合模型的預測結果；第七步進行誤差分析。預測的流程圖如圖2所示。

圖2 基于小波去噪的ARIMA-LSTM預測模型流程圖

2 實證分析

以原始的和經小波去噪后的2009年7月至2018年12月共計114個月的上證指數每日收盤價格作為訓練集，建立ARIMA模型處理數據的線性部分，再利用LSTM模型擬合非線性數據效果好的優點，對ARIMA模型無法擬合的殘差進行擬合，用ARIMA-LSTM混合模型對2019年1月至2019年6月共計6個月的上證指數每日收盤價格進行預測。

由Occam’s Razor法則知，誤差相同時模型越小其效果就會越好。因此常用AIC信息準則、BIC信息準則來對ARIMA模型進行定階。由于股票價格指數高波動性等因素，有時通過理論知識選出的最優模型不一定是預測效果最好的，所以根據不同的訓練集，分別建立幾組不同的模型，對模型檢驗后，用平均絕對誤差（MAE）和均方根誤差（RMSE）作為評價模型預測效果的標準進行預測誤差分析，選出不同訓練集下的誤差最小的模型。

在建立LSTM模型預測時，通過增加訓練次數來提高預測精度。在實證分析中參數Dropout設為0.2，采用3層神經網絡，時間步長設置為20，每批訓練60個樣本數據，學習率設為0.000 6，輸入層到隱藏層之間的激活函數使用tanh函數，預測時將訓練次數從800次增加到2 000次，每次訓練都增加100次并記錄結果。

建立不同模型在不同訓練集下的最優模型誤差對比如表1所示。

表1 不同訓練集下的最優模型誤差對比

根據表1的誤差對比可以看出：訓練集經小波去噪預處理后，再進行建模預測得到的預測結果要好于用未經預處理作為訓練集的預測結果，去噪后的混合模型和單模型預測效果圖、誤差對比分別如圖3、表2所示。

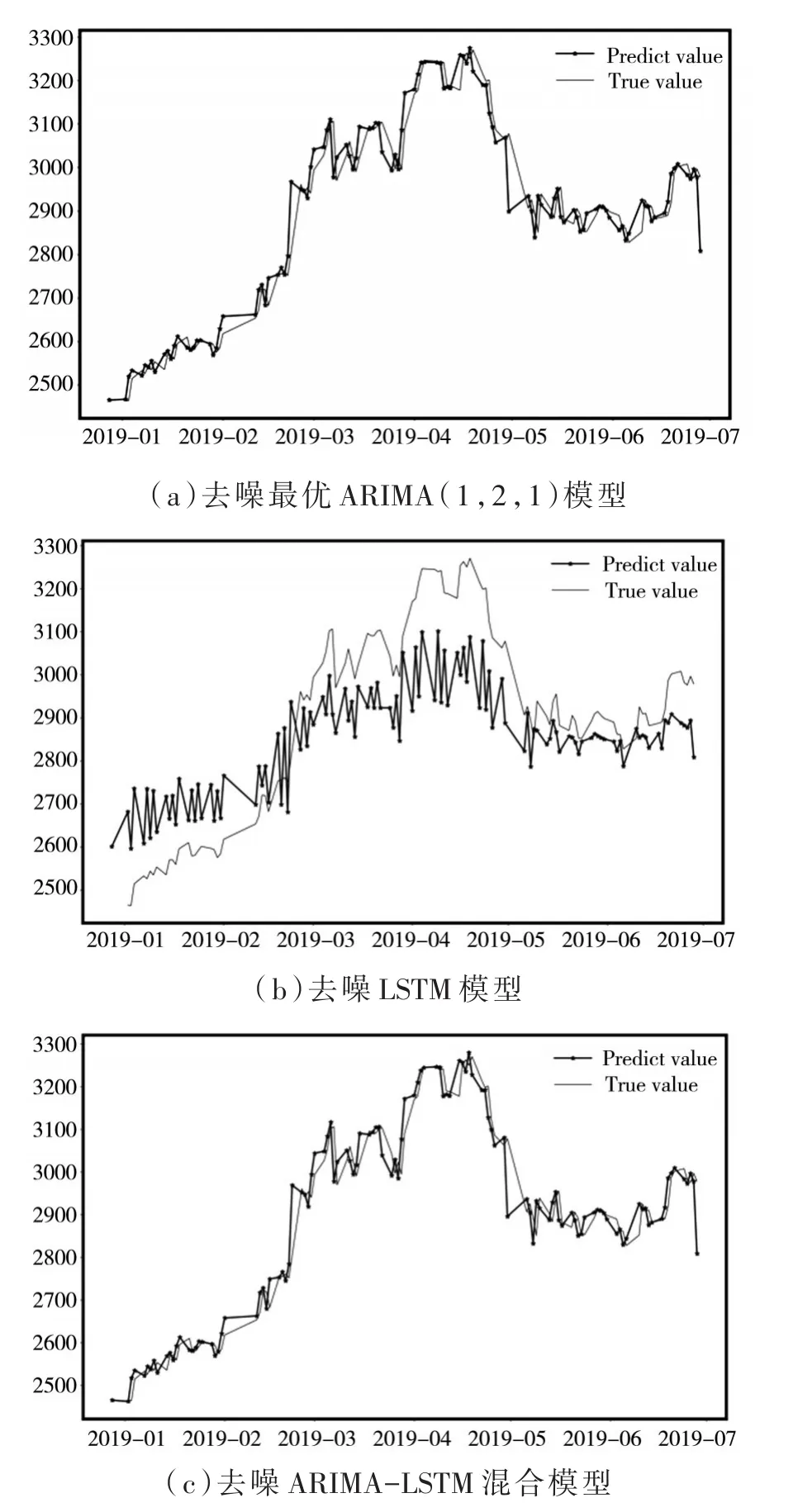
圖3 單模型和去噪后的混合模型預測效果圖

表2 三種去噪后的模型預測誤差對比

根據表2的誤差對比可以看出：第一，去噪后的ARIMA模型的MAE和RMSE均遠遠小于去噪后的LSTM模型，由此說明比起LSTM模型，ARIMA模型可以更好的擬合我國股票價格指數，而ARIMA模型主要用來擬合時間序列中的線性部分，所以股票價格指數中大部分數據是線性的，但是股票價格具有高波動性等不可控因素，因此對非線性因素預測也至關重要；第二，去噪后的ARIMA-LSTM混合模型的MAE和RMSE均稍微小于單獨建立去噪后的ARIMA模型的MAE和RMSE，因此建立LSTM模型對殘差進行擬合，將結果與單獨建立ARIMA模型預測的結果相加后得到結果更加接近真實值，所以去噪后的ARIMA-LSTM混合模型可以提高預測精度。

3 結論

通過實證分析對ARIMA模型、LSTM模型以及ARIMA-LSTM混合模型的預測效果進行了對比，結果表明基于小波去噪的ARIMA-LSTM混合模型對上證指數收盤價格進行預測效果最好，其次是ARIMA模型，最后是LSTM模型。這是因為股票價格指數中大部分數據是呈線性趨勢的，與LSTM模型相比ARIMA模型可以更好的擬合線性數據，所以單獨建立ARIMA模型預測的效果要比單獨建立LSTM模型的預測效果好；由于股票價格指數具有高波動性等因素，線性數據中也會參雜非線性數據，因此給出基于誤差補償思想的去噪ARIMA-LSTM混合模型，在建立ARIMA模型對線性數據擬合后，再建立LSTM模型對非線性殘差數據進行擬合，進一步提高了預測的精準度；該模型只適用于對我國上證指數的預測，并不適用于其它個股以及創業板指數的預測。