基于LSTM的COMEX黃金期貨價格預測對比研究

劉璐，婁磊，劉先俊，施三支

（長春理工大學 理學院，長春 130022）

黃金期貨市場在金融市場有著十分重要的位置，因此其預測問題也被視為重點問題。在預測方法上可分成傳統預測模型和非線性預測模型。傳統預測模型包含ARIMA模型（移動平均自回歸模型）、GARCH模型（自回歸條件異方差模型）、指數平滑模型等，并在黃金價格預測研究上取得了很大進步。比如在2014年，Sharma A M和Baby S[1]運用ARIMA模型對印度的黃金價格進行預測分析。同時，諸多學者也利用ARIMA模型對紐約商品交易所、倫敦國際金融期貨交易所、上海期貨交易所等具有明顯交易特點的黃金或黃金期貨交易數據進行建模預測[2-3]。在此基礎之上，一部分研究者運用了ARIMA-GARCH模型，對黃金價格進行了研究與分析[4-7]。比如潘貴豪等人[6]選用 ARMA-GARCH模型對黃金價格的動態演化過程進行了實證闡述，黃金價格數據的生成的動態變化過程可以被該模型精確的刻畫表明，平均誤差較小。傳統預測模型的各項研究均證明了其在預測黃金價格的走勢或動態特征方面是有效的，但是，鑒于黃金期貨價格時間序列具有非線性及高噪聲的數據特征，對其精確預測依舊十分困難，同時由于時間的動態變化，使得自變量和因變量二者之間的關系也會隨之發生變動，因此傳統時間序列模型很難精準得對黃金期貨市場進行預測。

近年來，隨著計算機硬件水平提升得越來越快，對神經網絡的研究也逐漸深入，由此非線性模型逐漸取代了時間序列模型在黃金期貨預測方面的應用，非線性預測模型包括基于ANN模型（人工神經網絡模型）及其演化的各種模型，如BPNN、SVR模型（支持向量回歸模型）、DNN模型（深層神經網絡模型）及其演化的各種模型，如CNN、RNN等。2010年曾濂等人[7]提出了一種基于BP神經網絡的改進模型，研究首先使用定性分析找到倫敦黃金期貨價格變動的影響因素，然后利用投影尋蹤方法篩選出非線性因素中影響力最大的因素輸入神經網絡，并改進算法進行網絡學習，最后訓練得出所需的BPNN[8]。基于淺層神經網絡對黃金期貨價格及趨勢進行預測的研究較之深層神經網絡的要多，包括ANN 模型[9]、基于 GA-BP神經網絡[10-12]、RBF神經網絡[13]、廣 義 回歸 神經 網 絡[14-15]和 SVR 模型[16-17]等等。

近年來，LSTM模型（長短期記憶網絡模型）開始逐步應用在金融序列預測問題上，眾多研究者開始利用LSTM模型對股票市場進行建模預測，2015年，Chen等人[17]將其運用于我國股票市場的股價預測，相較于其他預測模型，LSTM的預測效果得到了大幅提升。多個應用LSTM模型的金融序列預測，都獲得了更佳的預測效果[18-20]，但目前應用在黃金期貨市場預測上的研究成果相對較少。

綜上所述，為了尋找一種更合適的黃金期貨價格預測方法，建立了多層及雙向LSTM預測模型。以COMEX黃金期貨價格序列為研究對象，先將原始黃金期貨價格序列進行歸一化處理，然后進行不同參數下模型的比較，最后，選擇出最適應歸一化數值下的參數模型，輸出預測的結果。結果表明，雙向LSTM模型預測精度得到了明顯的進步，也驗證了模型的有效性。

1 基于LSTM的預測模型

傳統的黃金期貨價格預測模型不能充分描述黃金期貨價格很強的非線性、非平穩性和高噪聲的特點，因此在預測問題上存在許多困難，而神經網絡能夠發現并刻畫數據自身復雜的內部結構特征，也能自適應得學習和構建數據的非線性的復雜關系，不會對輸入變量施加限制，也具備更好的遷移學習（transfer learning）性質，因此非常適合處理如黃金期貨價格這樣的金融數據。其中LSTM模型更是經由丟棄和保留的機制有效解決了梯度反傳進程中產生的梯度消失（vanishing gradient problem）與梯度爆炸（explod?ing gradient problem）問題。由于LSTM能夠對信息進行全局化處理，因此其更適合于處理和預測時間序列。因此，本文建立了一個基于LSTM的雙向網絡預測模型，該模型僅基于相關黃金期貨價格的時間序列數據，不考慮其他影響因素，因此有效地消除了數據輸入變量和模型參數的不確定性。

1.1 LSTM模型基本原理

LSTM網絡模型最早由Hochreiter和Schmidhu?ber（1997）[20]提出。LSTM 每一個神經元的結構如圖1所示，其內部包括一個細胞狀態（Cell）和三個門控（Gates）設置，細胞狀態（Cell）記錄神經元狀態，綜合隱藏和時間步的事件，通常是經由三種門控機制實現這類記憶方式，即輸入門（Input Gate）、遺忘門（Forget Gate）和輸出門（Out?put Gate）。輸入門和輸出門用來接收、輸出和修正參數，遺忘門用來決定上一單元狀態信息的保留程度。

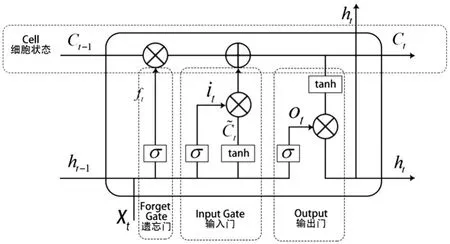
圖1 LSTM單個神經元結構圖

圖1中ht、Xt、tanh和σ分別表示t時刻細胞的輸出狀態值、t時刻細胞的輸入狀態值、雙曲正切函數前饋網絡層和sigmoid函數前饋網絡層，?表示點乘，⊕表示向量拼接。經由拼接向量乘上權重矩陣之后，再經由激活函數轉換來作為一種門控狀態。下面介紹各個門控的計算原理及過程。

首先計算t時刻下遺忘門（Forget Gate）的激活值ft，公式如下：

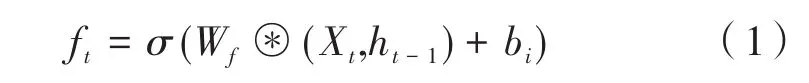
其次計算t時刻下輸入門（Input Gate）it的值和輸入細胞的候選狀態（Cell）的值，公式如下：

由以上計算可以得到t時刻下的細胞狀態（Cell）的更新值Ct，公式如下：

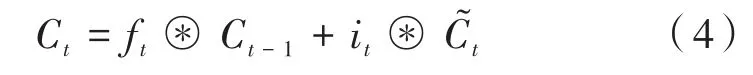
在計算得到細胞狀態（Cell）更新值后，最后就可以計算輸出門（Output Gate）的值，其計算公式如下：

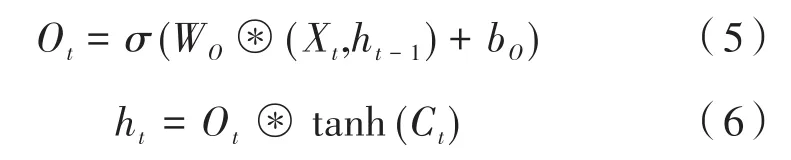
通過以上的計算，LSTM就可以確定最終的輸出值。

1.2 多層LSTM與雙向LSTM模型構建及結構

在Windows10操作系統下搭建Python的keras框架。keras包含兩種模型，一種是Sequential模型，另一種是Model模型，本實驗選用Model模型來搭建多層的LSTM網絡模型以及雙向LSTM模型分別對數據進行分析預測。

多層LSTM模型是將單層細胞狀態（Cell）進行堆疊，把每層神經元的個數都藏到Cell中間，其優點是可以更抽象的表達模型特征，并且按照數據特征，有效改善預測效果，但并非絕對的。有時針對簡單的數據，多層LSTM的預測效果反而會因為過擬合而降低準確率。多層LSTM不是定義一個基礎細胞狀態之后屢次調用，而是每次都界定一個新的基礎細胞狀態。也就是說，前一層的LSTM的輸出就是后一層的輸入，即輸入數據整體上是一個時間序列，而對每個內層特征數據來說，輸入數據也是一個時間序列及二維數組，因此也可以稱為數組的數組。舉一個簡單的例子：一個雙層LSTM模型，第一層的隱藏神經元個數是128，第二層的隱藏神經元個數為64，在t時刻的輸入向量是一維的。那么經過第一層的計算以及Cell的操作，第一層的輸出就會變成128維。疊加第二層LSTM后，此時第二層的t時刻的輸入即為128維，同樣的道理，經過運算其輸出為64維。最后經過Cell的操作，最終的輸出維度變為一維。

雙向LSTM模型是隱藏層要保留兩個值，C參與正向計算，C'參與反向計算。對于每個時刻t，輸入向量會同時賦值于兩個方向的LSTM并進行計算，這兩個單向LSTM同時影響著最后的輸出。在正向計算時，前饋層的ht與ht-1有關；而反向計算時，反饋層的ht則與ht+1有關。

多層LSTM網絡模型以及雙向單層LSTM模型的結構如圖2、圖3所示。

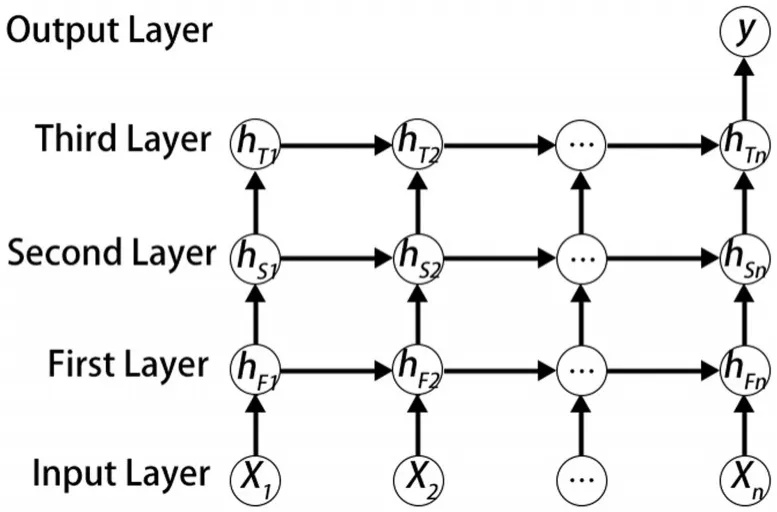
圖2 三層LSTM神經網絡結構

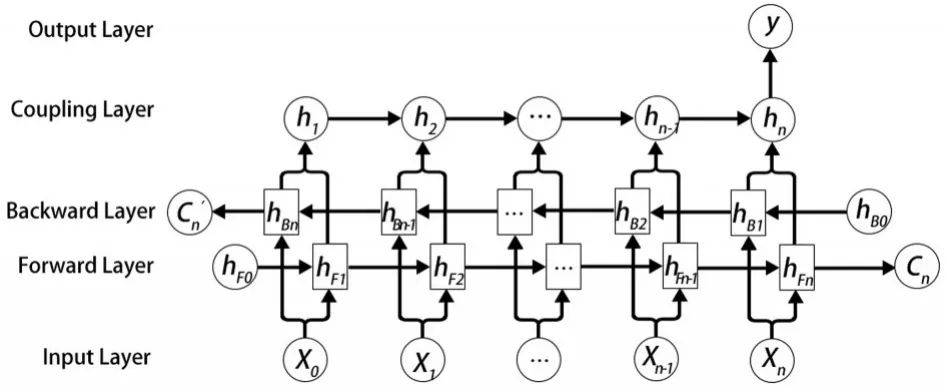
圖3 雙向單層LSTM神經網絡結構

2 實證分析

所有數據均來源于相關財經網站，由于2008年全球性金融危機對金融市場產生了非常大的影響，使得金融市場發生了很大的震蕩，因此2008年以前的數據研究意義較差，本文選取的數據范圍為2009年1月1日到2018年12月31日，共10年2 698個數據。

數據選取的是紐約商品交易所COMEX分部的黃金期貨數據，由于世界黃金期貨市場中，紐約商品交易所（COMEX）的黃金期貨指數發展較為成熟，同時美國財政部以及國際貨幣基金組織（IMF）也在此處進行相關買賣交易，是以COMEX的交易量占全球主導位置，也經常主導全球金價的走向，所以本文選擇COMEX黃金期貨價格數據作為研究對象。

2.1 數據預處理及模型的評價指標

為避免LSTM對輸入數據的限制，同時也有利于提高模型性能，加快訓練網絡的收斂性，在對序列進行量化分析前，首先將數據進行歸一化處理。根據選取數據的特點和LSTM的要求，本文采用線性函數歸一化方法對數據進行預處理。公式如下：

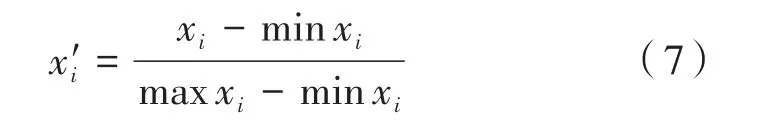
其中，xi代表第i個變量；minxi、maxxi分別代表xi的最小值與最大值。

對于黃金期貨價格這類數據規模及范圍不是非常大的情況，實驗模型的預測性能評價指標采用均方根誤差（RMSE）、平均絕對誤差（MAE）、平均誤差百分比（MAPE）、擬合度（R2）對實驗結果進行對比。其中RMSE、MAE、MAPE、R2的計算公式如下：

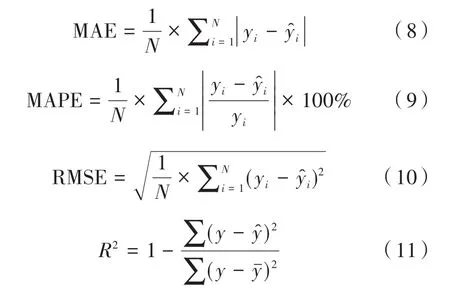
其中yi、y?i分別代表實際值與預測值，N代表預測窗寬.

2.2 實驗數據及超參數設置

模型初步建立后，為了使模型更加適合本數據，首先對單層模型進行了模型內部的參數優化。為了確定最合適的數據量，本文將數據分成了6組（分別是近5年、6年、7年、8年、9年和10年）在數據按上述方式確定數據特征及標簽后，在測試集均為2019年上半年的數據的情況下（2019.01.01-2019.06.30），當訓練集年限為9年（即2 068個數據）時，模型在測試集上的預測效果最佳。因此本文將2010年至2018年的數據作為TrainSet（訓練集），2019年1-6月的數據作為TestSet（測試集），負責訓練模型的召回率和正確率，最后訓練集據按9∶1的比例劃分，最后10%的數據作為ValidationSet（驗證集），負責調整模型相應的超參數以及模型的過擬合現象。實驗用數據集劃分如表1所示。

表1 數據集實驗數據劃分

對實驗參數進行選擇，在不同神經元個數的情況下在訓練集和測試集上進行預測，當單向單層LSTM模型的神經元個數為128時，模型在測試集上的預測效果最佳；在不同迭代次數的情況下對在訓練集和測試集上進行預測，當次數為500時，模型在測試集上的預測效果最佳；激活函數則同時選取了tanh及relu函數以緩解梯度消失問題；在不同訓練步長的情況下，訓練步長為3時，模型在測試集上的預測效果最佳；神經網絡優化算法使用Adam來更新參數，并應用dropout機制來規避實驗的過擬合.表2是實驗所用參數的具體說明。

表2 實驗參數

2.3 模型性能評價與結果比較

本文中采用ARIMA模型、RNN模型、SVR模型、雙層LSTM模型、雙向單層LSTM模型來進行對比實驗，通過比較測試集上MSE、RMSE、MAE、R2的值來進行優劣評判。同時實驗還在各個模型中嵌入了回調參數（totaltime），以計算不同模型下數據預測運行的時間。實驗對比結果如圖4所示，并將對比結果進行了整理，如表3所示。

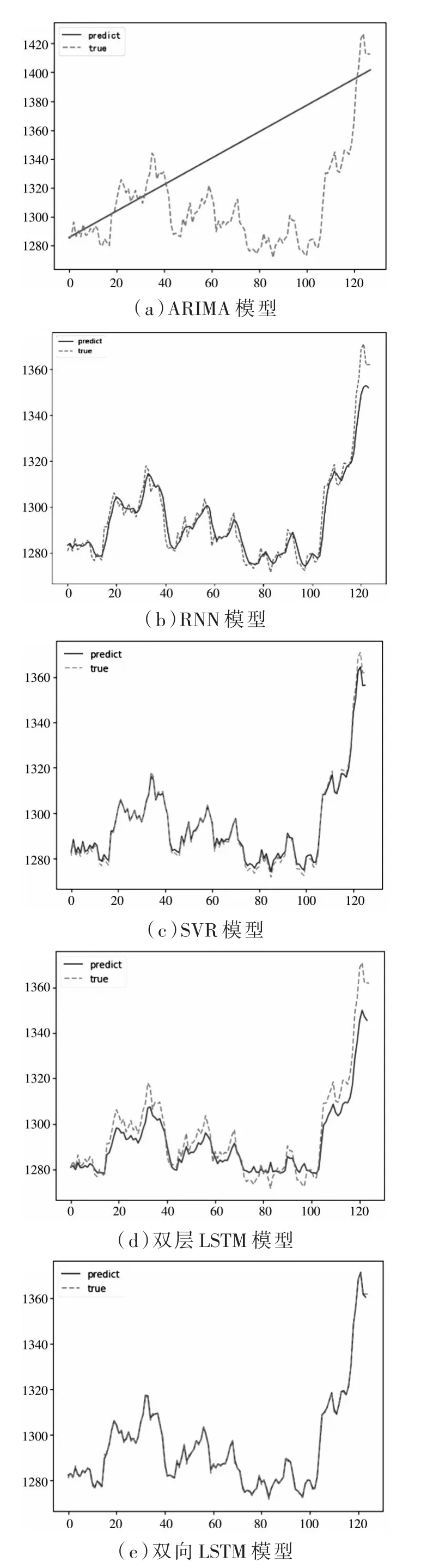
圖4 各模型預測結果

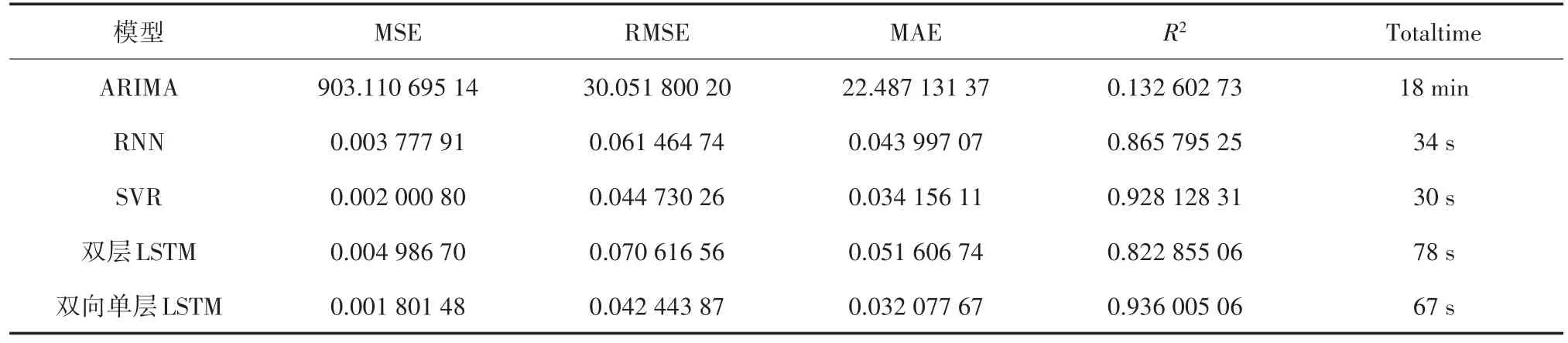
表3 對比結果

對比表3的實驗結果可以看出，在LSTM模型中，預測效果并未隨著模型層數增加而變好，反而出現了過擬合現象。這說明多層LSTM模型并不適用于本文所選用的數據信息。但本文給出的雙向LSTM模型相比于ARIMA模型、RNN模型、SVR模型、雙層LSTM模型，雙向LSTM模型評價指標 RMSE、MAE、MAPE、R2超過了所有對比的模型，達到了較好的效果，預測模型均得到了良好的提升，同時在確保預測準確性的前提下，雙向LSTM模型和SVR模型的運行時間較短。綜上，說明本文給出的雙向LSTM模型對于黃金期貨價格預測效果的提升是有效的。

3 結論

對于黃金期貨市場來說，只要知道近期黃金期貨的走勢以及價格，就對投資者的選擇帶來有價值的參考。本文將深度學習方法應用在黃金期貨價格預測方面，可以看出LSTM神經網絡既承繼了RNN在處理序列問題上的優點，又進一步提升了時間序列數據的高精度的預測結果。通過對黃金期貨價格數據進行歸一化等預處理操作后，對LSTM神經網絡的各項參數作出調整，并引入了dropout機制，對實驗結果進行比較，探索出適宜的雙向網絡模型，實現對COMEX黃金期貨價格序列的分析預測，通過觀察RNN模型、SVR模型、雙層LSTM模型和雙向LSTM神經網絡的表現，可以發現雙向LSTM模型在黃金期貨價格預測方面有較好的使用前景，下一步可研究如何在LSTM網絡引入其他模型并構成混合模型，進一步提高其預測精度。