非自治隨機p-Laplacian格點方程的后向緊隨機吸引子

宋 立，李揚榮

西南大學 數學與統計學院， 重慶 400715

若隨機吸引子的后向并是預緊的， 則稱該吸引子為后向緊隨機吸引子． 文獻[1-2]對非自治動力系統所產生的拉回吸引子的存在性和后向緊性做了深入的研究， 并建立了相對完善的理論體系． 文獻[3-6]對非自治方程的吸引子的存在性進行了研究， 文獻[7-8]對自治p-Laplacian格點方程吸引子的存在性做了研究． 本文將在文獻[8]的基礎上， 研究非自治情況下， 帶有乘法噪音的隨機p-Laplacian格點方程的后向緊吸引子的存在性．

1 預備知識

θt(s+t， ·)=θt(t， ·)°θt(s， ·) ?t，s∈R

則稱(Ω， F，P，θ)是一個度量動力系統．

則稱映射Φ是關于(Ω， F，P，θ)的非自治動力系統， 也稱協循環．

定義4令B是X的所有有界非空子集族構成的集合， 假設集合

K={K(τ，ω)：τ∈R，ω∈Ω}∈B

若對任意的τ∈R，ω∈Ω，D∈B， 存在T=T(τ，ω，D)>0， 使得當t≥T時有

Φ(t，τ-t，θ-tω，D(τ-t，θ-tω))?K(τ，ω)

則稱K為Φ的B-拉回吸收集．

2 非自治隨機動力系統

本文將在l2空間上討論帶有乘法噪音的非自治隨機p-Laplacian格點方程

(1)

其中Z代表整數集，λ，α>0，p>2，W(t)是雙邊實值Wiener過程， °代表Stratonovich積分意義下的乘法噪音． 對于外力項f=(fi)i∈Z和非自治項g=(gi)i∈Z有如下假設：

fi(s)s≤0 ?s∈R

(2)

(3)

(4)

定義l2上的有界算子：

B： (Bu)i=ui+1-uiB*： (B*u)i=ui-1-ui

A： (Au)i=|ui-ui-1|p-2(ui-ui-1)-|ui+1-ui|p-2(ui+1-ui) ?u∈l2

因此， 根據算子的定義， 有

(5)

微分方程(1)可整理為

(6)

下面證明方程(6)能生成隨機動力系統．

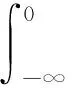
(7)

因此方程(6)可轉化為關于v的隨機微分方程

(8)

由文獻[8]可知， 對任意T>0，v0∈l2，ω∈Ω， 方程(8)存在唯一的解v(·，τ，ω，v0)∈C([τ， +∞)， l2)， 且依賴初值v0連續． 因此方程(8)在(Ω， F，P， {θt}t∈R)上能生成一個連續的隨機動力系統{Φ(t)}t≥0， 即對v0∈l2，t≥0，τ∈R， 和ω∈Ω， 有

Φ(t，τ，ω，v0)=v(t+τ，τ，θ-τω，v0)

在下文中， 設D0是X中所有緩增集構成的集合， D是X中所有后向緩增集構成的集合． 若集合D0滿足

(9)

則稱集合D0為緩增集； 若集合D滿足

(10)

則稱集合D為后向緩增集．

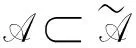
3 解的估計

引理1若假設(F1)，(F2)成立， 那么有：

(11)

其中R0(τ，ω)是可測函數， 定義為

(12)

(13)

其中

(14)

證對任意固定的τ∈R，ω∈Ω，vs-t∈D(s-t，θ-tω)， 令v(r)=v(r，s-t，θ-sω，vs-t)， 其中s≤τ．v(r)與方程(8)作內積可得

(15)

利用(2)，(5)式整理(15)式， 可得

(16)

利用H?lder不等式及Young不等式， 有

(17)

代入(16)式可得

(18)

對(18)式利用Gronwall不等式， 計算可得

(19)

再由(7)式、 (9)式可知， 存在T0(D0，s，ω)≥1， 使得當t≥T0時， 有

(20)

因此(11)式得證．

對(19)式關于s∈(-∞，τ]取上確界， 由于vs-t∈D(s-t，θ-tω)(s≤τ)， 結合(7)式、 (10)式可知， 存在T=T(s，ω， D)≥1， 使得當t≥T時， 有

(21)

因此可以得到

(22)

即(13)式得證．

注射碘酊治療組:1周后,囊腫注射部位的粘膜表面發白,無觸痛,3周后,注射部位與周圍粘膜無差異,囊腫已完全消失,表面粘膜未見異常,半年內進行隨訪,見6例囊腫復發。

引理2若假設(F1)，(F2)成立， 則有如下結論：

K0(τ，ω)={w∈l2： ‖w‖2≤1+R0(τ，ω)} ?τ∈R，ω∈Ω

(23)

(24)

首先證明R(τ，ω)是有限的． 根據(7)式可知， 對任意ε>0， 存在C=C(ε，ω)>0， 使得

(25)

(26)

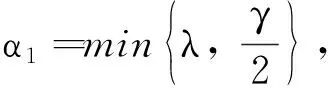
(27)

所以K∈D0． 又由于K0?K， 因此K0∈D0．

最后證明K∈D． 根據(24)式， 易知集合K是遞增的， 即

K(τ1，ω)?K(τ2，ω) ?τ1<τ2

因此， 結合K∈D0可知， 對任意γ>0， 有

(28)

即證得K∈D． 再由(13)式可知， K在任意集合D∈D上是后向一致吸收的．

引理3若假設(F1)，(F2)成立， 則對?ε>0， (τ，ω， D)∈(R×Ω×D)，vs-t∈D(s-t，θ-tω)， 存在T(ε，τ，ω， D)>0，N(ε，τ，ω， D)≥1， 使得

證構造光滑函數ρ， 滿足0≤ρ≤1， 且當|s|≤1時，ρ=0； 當|s|≥2時，ρ=1． 并假設存在常數c0， 使得對任意s∈R， 有|ρ′(s)|≤c0． 令N是一個固定的整數， 設

x與(8)式作內積可得

其中

(29)

由于|ρ′(s)|≤c0， 因此

(30)

故由(29)式、 (30)式可得

(31)

由假設(F1)可知

(32)

由Young不等式可知

(33)

結合(31)-(33)式， 可得

(34)

對(34)式運用Gronwall引理， 計算整理可得

(35)

由于vs-t∈D(s-t，θ-tω)(s≤τ)， 結合(7)，(10)式可得

(36)

(37)

(38)

因此， 結合(36)-(38)式可得， 對任意的ε>0， (τ，ω， D)∈(R×Ω×D)，vs-t∈D(s-t，θ-tω)， 存在T(ε，τ，ω， D)>0，N(ε，τ，ω， D)≥1， 使得

引理4若假設(F1)，(F2)成立， 則協循環{Φ(t)}t≥0在吸收集K∈D上是后向漸近緊的．

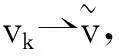
證對任意固定的τ∈R，ω∈Ω， 取任意序列{τk}≤τ， {tk}→+∞(k→+∞)， 及任意的v0∈K(τk-tk，θ-tkω)． 定義vk=Φ(tk，τk-tk，θ-tkω，v0)=v(τk，τk-tk，θ-τkω，v0)， 下證{vk：k∈N}在l2中是預緊的．

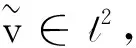
(39)

下面只需證明該弱收斂實際上是強收斂， 即只需證明：

對任意ε>0， 存在T>0和K≥1， 使得當k>K時， 有

(40)

注意到

(41)

一方面， 由引理3可知， 對任意ε>0， 存在T1>0，N1，K1≥1， 使得當k>K1時， 有

(42)

(43)

由(42)-(44)式可知， 令

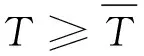
即證得協循環{Φ(t)}t≥0在吸收集K上是后向漸近緊的．

4 后向緊隨機吸引子

定理1若假設(F1)，(F2)成立， 則方程(1)生成的動力系統存在后向緊隨機吸引子．

證引理2和引理4的結論滿足了文獻[11]的定理3.9中拉回吸引子的存在性條件， 因此方程(8)生成的非自治隨機動力系統Φ(t)存在唯一的后向緊D-拉回吸引子A∈D， 和唯一的可測D0-拉回吸引子A0∈D0． 再由文獻[9]的定理6.1知A=A0， 故吸引子A也是隨機的， 即Φ(t)存在唯一的后向緊D-拉回隨機吸引子A∈D． 再由文獻[12-13]知方程(1)與方程(8)生成的隨機動力系統共軛， 進而可知方程(1)存在后向緊隨機吸引子．