時頻分析聯合帶通濾波抑制間歇采樣轉發干擾

孫正陽，董 玫，陳伯孝

(西安電子科技大學 雷達信號處理國家重點實驗室，陜西 西安 710071)

數字射頻存儲器(Digital Radio Frequency Memory，DRFM)是雷達對抗領域廣泛采用的重要設備，它具有接收、存儲、調制和轉發雷達信號的能力。DRFM產生的相干干擾信號可以在雷達接收機中獲得相干處理增益，生成假目標干擾雷達系統[1-2]。

基于DRFM的轉發式干擾大致可以分為全脈沖轉發和部分脈沖轉發兩種模式。傳統的相干轉發式干擾通常要截獲完整的雷達脈沖信號進行不失真的采樣轉發。這種工作方式產生的干擾在雷達采用頻率捷變或波形分集等抗干擾技術時可能失效[3-4]。同時，在彈載等應用場合，此類干擾對寬帶信號采樣率和收發天線隔離度的高要求難以實現。文獻[5]提出了一種部分脈沖轉發的干擾樣式，稱為間歇采樣轉發干擾(Interrupted Sampling Repeater Jamming，ISRJ)。對于截獲到的雷達信號，ISRJ干擾機先采樣其中一段信號進行轉發，再采樣并轉發下一個信號片段直到雷達信號結束。ISRJ信號經過脈沖壓縮后會在距離向上生成一個或多個假目標群，嚴重影響雷達對真實目標信息的獲取。

ISRJ的改進及其在多種體制雷達中的應用已有大量研究，但當前針對ISRJ的抗干擾技術研究還比較欠缺。目前，在信號與數據處理層面的ISRJ對抗算法研究主要有信號重構[6-7]和頻域濾波[8-11]兩種思路。

基于信號重構的思想，文獻[6]通過時頻分析和反卷積處理估計干擾信號參數，然后重構干擾信號，并通過迭代對消抑制干擾。這種方法十分依賴對干擾信號參數的準確估計，且計算量較大。文獻[7]定義了能量函數，根據干擾信號與目標回波信號間的能量函數差異提取無干擾目標信號數據，然后通過壓縮感知理論重構目標回波信號，從而實現對ISRJ的抑制，但文中僅分析了較高信噪比條件下的算法性能。

基于頻域濾波的思想，文獻[8-11]針對去斜體制雷達，設計算法提取時域接收信號中的無干擾信號片段，并以此構造頻域帶通濾波器實現對ISRJ的抑制。具體而言，文獻[8-9]基于短時傅里葉變換(Short Time Fourier Transform，STFT)構造功率函數，并由此確定無干擾信號的時域區間。該算法可以有效抑制干擾，但依賴干擾采樣次數和干擾采樣時間兩個超參數。文獻[10]將時域信號的模平方定義為能量函數，基于能量函數確定無干擾信號的時域區間，并設計窗函數抑制濾波器的旁瓣。該算法構造出的頻域帶通濾波器具有很低的旁瓣，但只能針對單目標情況。同時，該算法在低信噪比(Signal to Noise ratio，SNR)和低干信比(Jamming to Signal Ratio，JSR)條件下性能欠佳。文獻[11]基于STFT構造max-TF函數，結合全局閾值和局部閾值迭代計算無干擾信號的時域區間。該算法可以精確提取無干擾信號片段，且適用于多目標情況，但這種基于無干擾信號片段提取的干擾抑制方法在多目標情況下會造成部分目標在干擾抑制后出現明顯的幅度損失。

針對上述問題，結合信號重構與頻域濾波的思想，首先通過數個脈沖重復周期接收信號的時頻域積累，實現低信噪比下信號時頻信息的增強；然后結合圖像處理算法在時頻面上準確提取干擾分布區域，并通過時頻域濾波將干擾濾除，粗略重構目標回波時域信號；再由重構的時域信號構造頻域帶通濾波器，實現對干擾和噪聲的抑制。該算法可以在低信噪比、多目標環境下有效抑制多種類型的ISRJ，且不造成明顯的目標幅度損失。

1 信號模型與時頻特性分析

1.1 信號模型

根據干擾機具體轉發策略的不同，ISRJ可以被劃分為間歇采樣直接轉發干擾(Interrupted Sampling and Direct Repeater Jamming，ISDRJ)[5]、間歇采樣重復轉發干擾(Interrupted Sampling and Periodic Repeater Jamming，ISPRJ)[12]和間歇采樣循環轉發干擾(Interrupted Sampling and Cyclic Repeater Jamming，ISCRJ)[13]等。筆者針對ISDRJ、ISPRJ和ISCRJ這3種干擾進行分析。圖1展示了3種干擾的基本工作原理。

圖1中，1-1表示第1個采樣片段的第1次轉發，1-2表示第1個采樣片段的第2次轉發，2-1表示第2個采樣片段的第1次轉發，以此類推。T為脈沖寬度，τ為干擾采樣片段寬度，Ts為干擾采樣周期。

幅度歸一化的線性調頻(Linear Frequency Modulation，LFM)發射信號可以表示為

(1)

設去斜處理中的混頻參考時延為τref，則參考信號可表示為

(2)

由于目標速度設置不影響文中結論，假設目標為位置固定的點散射體，目標與雷達間的徑向距離為Rtar，則與參考信號混頻后的目標回波信號可表示為

(3)

其中，Atar為目標回波信號的幅度；τtar=2Rtar/c，為目標回波信號的時延，c為光速。

結合圖1所示的各類型干擾的工作原理，同時考慮到ISDRJ與ISPRJ僅有轉發次數的不同，忽略干擾機的轉發時延，可將二者經混頻后的結果統一表示為

圖1 ISRJ的基本工作原理

(4)

ISCRJ經混頻后的輸出結果可表示為

(5)

1.2 時頻特性分析

瞬時頻率(Instantaneous Frequency，IF)是信號相位的導數，它可以反映信號的時頻特性。由式(3)，混頻后目標回波信號的瞬時頻率可表示為

(6)

由式(4)，混頻后ISPRJ信號的瞬時頻率可表示為

(7)

當式中M=1 時，式(7)即表示混頻后ISDRJ信號的瞬時頻率。

由式(5)，混頻后ISCRJ信號的瞬時頻率可表示為

(8)

由式(6)～(8)可以看出，在脈沖持續時間內目標回波信號的瞬時頻率是隨時間連續變化的，而ISRJ信號的瞬時頻率是間斷的。目標回波信號與ISRJ信號間存在的這種明顯的時頻分布差異為在時頻域區分二者提供了依據。同時，混頻后的目標回波信號和ISRJ信號分布在不同的恒定頻率上，因此可以通過設計一個與目標回波信號頻率相匹配的帶通濾波器實現對干擾信號的抑制。

時頻分析是分析非平穩信號的有力工具，它可以直觀地表示出信號的頻率成分隨時間變化的規律。STFT是一種常用的線性時頻變換，具有計算簡單、不產生交叉項的優點。文中采用STFT對信號進行時頻分析。已知信號x(t)，其時頻分布可表示為

(9)

其中，Γ{·}表示STFT運算，ω(·)表示STFT中的窗函數。

圖2展示了在各類型ISRJ信號存在條件下，混頻后雷達接收信號的STFT時頻分布仿真圖。設置2個目標，其中的目標1施放自衛式干擾。為方便觀察，不考慮噪聲的影響，JSR設置為5 dB。

圖2中較長的線段表示目標回波信號的時頻分布，其他多個較短的線段表示干擾信號的時頻分布。仿真圖中信號的時頻分布特性與前文理論分析一致。

2 干擾抑制算法流程

2.1 時頻信息增強

在STFT時頻分布中，目標回波信號或ISRJ信號的能量聚集在各自的IF曲線附近，而高斯白噪聲的能量則散布在整個時頻面上。當噪聲較弱時，信號(目標回波與干擾)的時頻特征明顯。但在強背景噪聲下，信號的時頻信息會被噪聲“淹沒”，這將嚴重影響對信號時頻信息的提取。

考慮到噪聲的時頻分布具有隨機性，而對于極短的觀測時間，可以忽略目標的位置、速度等狀態變化且假設干擾機未改變干擾策略，因而可以認為不同脈沖重復周期回波中信號的時頻分布具有確定性。文中采取多脈沖回波時頻譜圖累加平均的策略來增強信號的時頻信息。

譜圖(Spectrogram)定義為信號STFT的模值平方[14]，即有

(10)

L個脈沖重復周期回波的時頻譜圖積累后的結果為

(11)

其中，Ψl(t，f)表示第l個脈沖重復周期回波的時頻譜圖。

以ISPRJ為例，圖3(a)展示了SNR為-10 dB，JSR為5 dB情況下單個脈沖重復周期回波的歸一化譜圖。可以看出，在強噪聲背景下，信號的時頻信息被噪聲“淹沒”，無法直接從時頻面上提取信號的時頻信息。對16個脈沖重復周期回波的時頻譜圖進行積累并歸一化處理，結果如圖3(b)所示。可以看出，文中采用的時頻信息增強方法使得時頻面上信號的時頻特征變得明顯。

(a) 間歇采樣直接轉發干擾

(a) 時頻信息增強前

(a) 二值化

2.2 時頻圖像處理

2.2.1 二值化處理

最大類間方差法(Otsu)是一種自適應的二值化閾值確定方法。它按照圖像的灰度特性將圖像分為目標和背景兩類，以目標與背景的類間方差最大為閾值選取準則。Otsu計算簡單，適合于實時處理。針對時頻信息增強后的時頻圖，文中采用Otsu算法計算閾值，并將其二值化處理：

(12)

其中，Τ1(t，f) 表示二值化時頻圖，γ表示二值化閾值。

二值化處理進一步濾除了噪聲，突出了信號的時頻分布，但時頻面上可能殘留的孤立噪點、結構間的粘連、結構邊緣的毛刺和結構中的斷裂仍會影響時頻信息的提取，形態學處理可以用來消除這些影響。

2.2.2 形態學處理

數學形態學是以形態結構元素為基礎對圖像進行分析的數學工具，它可以用來簡化圖像數據，在去除圖像中不相關結構的同時保持圖像的基本形狀特征。其基本運算包括腐蝕、膨脹、開運算和閉運算等。其中開運算和閉運算由腐蝕和膨脹操作的不同級聯得到。先腐蝕再膨脹即為開運算，它可以用于濾除圖像中不能包含結構元素的細小結構，斷開結構間纖細的連接，平滑較大結構的邊界；先膨脹再腐蝕即為閉運算，它可以用于填充細小空洞，修補結構中的裂縫。

對二值化時頻圖先開運算再閉運算，消除圖像中可能殘留的噪點并修補IF曲線中可能出現的斷裂。形態學處理后的二值化時頻圖可表示為

Τ2(t，f)=(Τ1(t，f)ΘE⊕E)⊕EΘE，

(13)

其中，Θ表示腐蝕運算，⊕表示膨脹運算，E表示結構元素。結構元素的選取會影響形態學處理結果，設計與圖形匹配的結構元素有利于提高形態學處理的效果。基于去斜后信號的時頻特征，筆者設計了一個水平的短的線性結構作為結構元素。

2.2.3 連通區域分析

形態學處理后的時頻面上存在著多個連通區域，每一個連通區域都代表一個干擾片段或目標回波信號。如果能對這些連通區域進行劃分，就可以在時頻面上對干擾進行定位，進而將其濾除。

使用8連通準則對形態學處理后的二值化時頻圖中的連通區域進行標記，即如果兩個像素都為1且在水平、垂直或對角線方向上鄰接，則認為它們屬于同一個區域。通過連通區域分析，可以獲得各連通區域的質心、外接矩形等幾何參數。同時，由于發射信號脈寬已知，目標回波信號與發射信號脈寬近似相等，而干擾片段的脈寬小于發射信號脈寬的一半[7]，因而可以通過連通區域的時間寬度區分目標回波區域和干擾區域。

圖4展示了圖3(b)在時頻圖像處理各個步驟中的輸出結果。在圖4(c)所示的連通區域檢測結果中，為便于觀察，檢測出的目標回波區域的時頻點取值設置為0.5，檢測出的干擾區域的時頻點取值設置為1。需要說明的是，為體現算法性能，設置了較低的JSR。實際上，為了保證干擾的有效性，干擾機通常需要結合干擾采樣占空比等參數設置較大的干擾功率[5]。在大JSR條件下，文中算法的時頻圖像二值化結果中將不會保留目標回波信號的時頻信息，但這并不影響算法的有效性。

2.3 干擾抑制

首先，基于連通區域分析的結果構造時頻掩膜X(t，f)，以將干擾所在頻帶內的時頻點取值設置為0，時頻面上其他部分的時頻點取值保持不變，即

(14)

將構造的時頻掩膜與混頻后接收信號的STFT時頻分布相乘，得到掩膜后的時頻分布，再對其做短時傅里葉逆變換(Inverse Short Time Fourier Transform，ISTFT)，即可得到重構的時域信號

si(t)=Γ′{Ωs(t，f)⊙Χ(t，f)} ，

(15)

其中，Γ′{·}表示ISTFT運算，Ωs(t，f)表示混頻后時域接收信號s(t)的STFT時頻分布，⊙表示Hadamard積。

實際上，重構信號中的干擾成分已被濾除，但其中大部分的噪聲成分仍被保留。為了在抑制干擾的同時盡可能地抑制噪聲，用重構的時域信號si(t)進一步構建歸一化的帶通濾波器

(16)

(17)

3 算法性能仿真分析

本節通過仿真分析，驗證文中提出的算法的有效性和穩健性。主要參數設置如表1所示，其中的采樣頻率為正交采樣時的頻率。定義脈沖壓縮前SNR和JSR的計算公式分別為

表1 仿真參數設置

(18)

其中，σ2表示噪聲功率。

3.1 算法有效性分析

以ISPRJ為例，圖5對比展示了基于能量函數的算法[10]、基于max-TF函數的算法[11]和本文算法在相同條件下的干擾抑制效果。其中，方框指示的區域為真實目標，其余多個尖峰為ISRJ所生成的假目標群。設置SNR為5 dB，JSR為15 dB。由圖5(a)可以看出，文獻[10]中的算法雖然可以大幅抑制干擾，但在多目標條件下僅有一個真實目標被保留而其他真實目標連同干擾一起被抑制。這是由于該算法在抑制濾波器旁瓣時依賴于對一個函數最大值的搜索，因而其構造出的頻域帶通濾波器僅有一個峰值，故只適用于單目標情況。由圖5(b)可以看出，文獻[11]中的算法可以在多目標條件下有效抑制干擾，但其中目標2經干擾抑制后有3.5 dB左右的幅度損失。這是由于2個目標的回波信號在時域被干擾信號遮蓋的范圍大小不同，所以基于時域提取無干擾信號片段構造的頻域濾波器的2個尖峰在幅度上有不可避免的明顯差異，最終導致被干擾信號遮蓋較多的目標回波其脈壓結果經濾波后有明顯的幅度損失。文中提出的算法可以在多目標條件下有效抑制干擾而不使目標幅度有明顯損失，且相對于文獻[11]中的方法，文中算法對干擾的抑制程度更強。

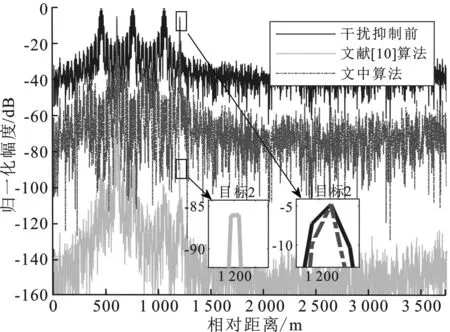
(a) 文中算法對比文獻[10]算法

(a) 間歇采樣直接轉發干擾

3.2 算法穩健性分析

采用信干比改善因子(Signal to Jamming Ratio Improvement Factor，SJRIF)作為指標，進一步衡量算法的穩健性。首先，定義脈沖壓縮結果中的信干比(Signal to Jamming Ratio，SJR)為

(19)

其中，ai表示第i個真實目標的幅度，I表示目標個數，aj是除目標外干擾或噪聲的最大幅度。信干比改善因子δ定義為

δ=RSJa-RSJb，

(20)

其中，RSJa表示干擾抑制后脈沖壓縮結果的信干比，RSJb表示干擾抑制前脈沖壓縮結果的信干比。

信噪比設置為-10 dB到10 dB，以2.5 dB為步長遞增；JSR設置為5 dB到20 dB，以5 dB為步長遞增。在每一個固定的SNR和JSR條件下，根據式(19)和式(20)計算每種ISRJ存在條件下的SJRIF。圖6展示了500次蒙特卡羅試驗的結果。可以看出，對于3種類型的ISRJ，文中算法的干擾抑制性能隨SNR的提升而逐步提升，且在低SNR和低JSR條件下也具有明顯的干擾抑制效果。

在相同的參數設置下，對文獻[11]中的算法同樣進行500次蒙特卡羅試驗。對于每種算法，將3種干擾存在條件下分別計算得到的SJRIF結果平均后取整處理，結果如表2所示。可以看出，相比于文獻[11]中的算法，文中提出的算法在所有的SNR和JSR條件下均有更好的干擾抑制性能。在JSR為5 dB的條件下，文獻[11]中的干擾抑制算法基本失效，而文中算法仍具有顯著的干擾抑制效果。同時可以看出，在低信噪比條件下，本文算法的優越性更加明顯。

表2 不同干擾抑制算法的SJRIF對比

4 結束語

筆者分析了目標回波信號與ISRJ信號的時頻特性，并基于時頻圖像處理和頻域濾波提出了一種新的ISRJ干擾抑制算法。首先，通過數個脈沖重復周期接收信號的時頻域積累實現信號時頻信息的增強；然后結合圖像處理的方法在時頻面上準確提取干擾分布區域，并基于提取的干擾信息在時頻域對干擾信號進行濾除，粗略重構目標回波信號；最后由重構的時域信號構造頻域帶通濾波器對干擾和噪聲進行抑制。仿真結果表明，所提出的算法可以在多目標條件下有效抑制ISDRJ、ISPRJ和ISCRJ等多種類型干擾。同時，算法具有較強的穩健性，在低信噪比下仍有良好的干擾抑制效果。