KNN 算法在高壓直流輸電單端故障檢測的應用

（國網福建省電力有限公司 福建福州 350003）

0 引言

高壓直流輸電（HVDC）工程在電能輸送、電網互聯方面起著非常重要的作用。與高壓交流（HVAC）輸電技術相比，高壓直流輸電技術由于其靈活的控制能力和大電能的輸送能力，在長距離輸電、異步電網互聯和可再生能源集成方面更具競爭力［1-2］。由于高壓直流輸電系統通常建設野外，所經過的路徑遠，可能經過特殊地形的環境等［3-4］，因此存在特定故障隱患。如何快速可靠地檢測并排除故障，關系到整個高壓直流輸電系統的運行安全［5］。

傳統的直流輸電線路故障檢測方法主要包括電壓或電流差分方法和行波方法。Anderson［6］使用電壓差率來檢測線路故障，Li S 等［7］提出了一種新型的橫向差動保護，利用差動電流和雙端電流差動率來建立標準。蔣靈通等［8］通過前、后波頭的準確檢測，提出了基于時差的縱聯方向保護。但是，差分方法受到故障電阻的影響很大，對波頭提取要求極高，無法正確識別高阻故障。Ma Y 等［9］將行波保護應用于雙回路傳輸線。Zhang Y 等［10］提出了一種基于零序和正序方向的行波保護方案，然而該方法容易受到干擾的影響，并且難以識別高阻故障。Kong F 等［11］通過單端數據分析反向行波的不同特性來實現故障檢測。Luo S 等［12］提出了一種基于無功潮流的雙端保護方案，可以在低采樣頻率下正常工作，但它需要兩個時間延遲周期。

最近，有部分學者將機器學習的方法應用于電網保護。文獻［13-14］通過人工神經網絡（ANN）學習輸入數據與目標值之間的關系，實現了交流配電系統小電流接地的故障保護。Johnson 等［15］使用支持向量機（SVM）來識別僅具有單端電壓和電流信號的HVDC 故障線路。Chen M 等［16］將KNN 和SVM 作為HVDC 系統故障區域檢測的分類機制。但是這些文獻里面提到的方法尚未很好地解決啟動組件的問題。李自乾等［17］通過公式推導消除行波波速的影響單端故障行波測距方法。郭敬梅等［18］結合故障條件中各因素對行波保護動作概率的影響程度，分析了運行方式變化帶來的不利影響。文獻［19-20］分析了KNN 在數據處理中具有良好的效率。張懌寧等［21］提出一種基于故障錄波數據的耐受高阻接地的直流接地極線路故障測距新方法。

目前，關于HVDC 故障檢測的研究，大部分選取的接地電阻均小于500 Ω。但在實際運行的電力系統，有的故障類型故障電阻比這個值高，甚至達數萬Ω。因此，在采樣頻率盡可能小的前提下，增加檢測系統的可測量電阻值上限是迫切需要解決的難題之一。

本文將K 最近鄰（KNN）引入高壓直流輸電系統，利用KNN 優秀的分類性能與小樣本訓練能力實現HVDC 系統快速故障檢測。本方法的采樣頻率為10 kHz，整流側檢測裝置采集到故障信號后直接作為KNN 模型的輸入，訓練好的KNN用于檢測故障區域，用PSCAD/EMTDC 建立高壓直流輸電模型，仿真結果表明該方法可以成功識別電阻高達1 000 Ω 的故障。本文介紹了所提出的故障檢測方法的基本原理，與基于反向行波的故障檢測方法進行了比較，并通過電磁暫態仿真軟件PSCAD/EMTDC 搭建±500 kV 高壓直流輸電系統，在不同故障區域與故障類別下對所提出方法的有效性進行評估驗證。

1 KNN 故障檢測方法

高壓直流輸電系統HVDC 包括：雙端交流系統、整流器、逆變器和輸電線路。線路邊界由直流濾波器和平滑電抗器組成，起到低通濾波的作用。無論直流輸電系統哪個部分發生故障，整流器側檢測裝置都將檢測到電壓突變。由于線路邊界和線路阻抗的影響，不同區域的故障波形將具有不同程度的幅度和平滑度。基于K-Nearest Neighbor（KNN）的故障檢測方法，流程圖如圖1 所示。整流側檢測裝置檢測到電壓突變后啟動檢測算法，采集到的故障波形通過事先訓練好的KNN 判斷器診斷是否為接地故障或者雙極短路故障。若KNN 判斷器診斷為是，則再由KNN 分類器區分故障為內部故障或者為外部故障以及故障發生在哪條輸電線路上。兩個KNN 均由各種故障區域和故障條件下采集到的電壓大量訓練，訓練好的KNN 用于實現故障檢測。

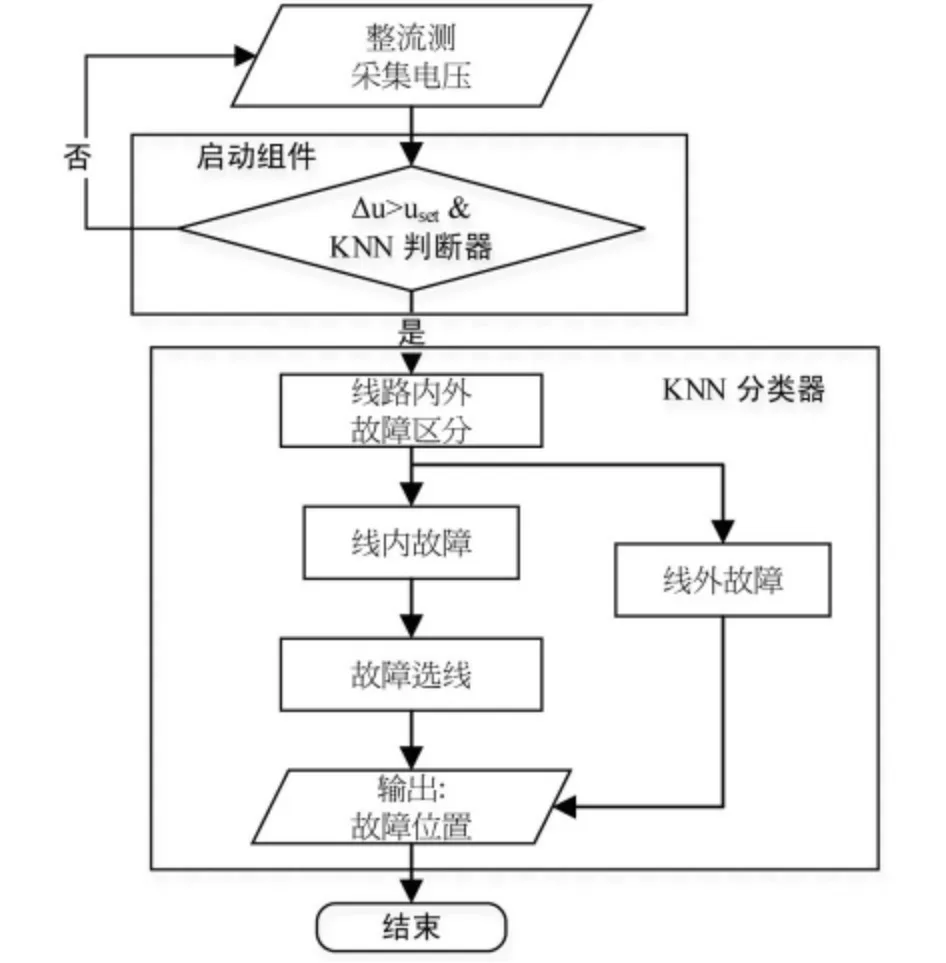
圖1 KNN 方法流程圖

1.1 KNN 算法

K-Nearest Neighbor（KNN）是一種監督學習分類器。作為經典分類算法之一，其核心思想包含未知樣本的空間中，如圖2 所示，可以根據最近鄰k 個樣本的數據類型確定樣本的數據類型。KNN 有三個主要因素：訓練集、距離和類似度量、以及k值［16，22］。

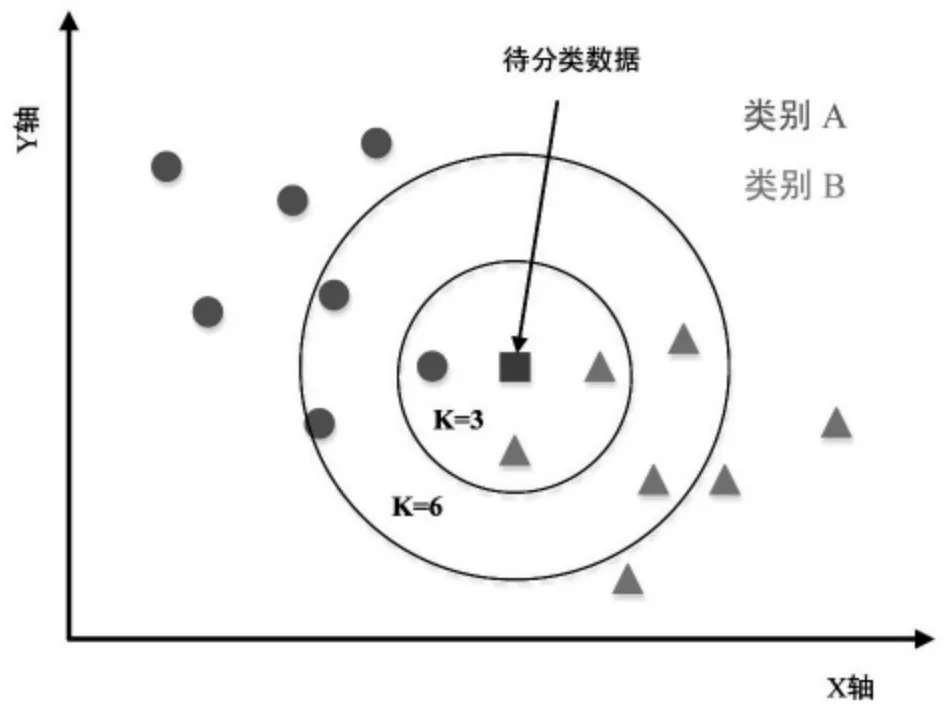
圖2 KNN 示意圖

對于一個測試樣本，需要計算該測試樣本與訓練集中的其他樣本之間的關系程度。不同的數據集擁有對應的最佳距離函數，常見的距離函數分別有：

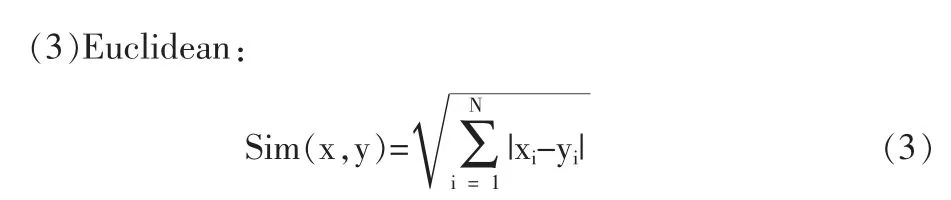
式中：特征向量S 表示協方差矩陣，Si是第i 維度中的樣本數據的標準偏差。首先，使用初始值確定k 值，然后根據實驗測試的結果調整k 值。其次，根據樣本的相似度，在訓練集中選擇與測試樣本最相似的k 個樣本。在k 個最近鄰樣本中，計算每個類別的權重，并通過比較權重將樣本分類到具有最高權重的類別［23］。

1.2 KNN 判斷器和KNN 分類器

受到文獻［24］的啟發，本文搭建兩個KNN 模型。第一個KNN 為判斷KNN，其作用是當檢測裝置采集到突變波形后，判斷該波形是否為接地故障或者為雙極短路故障。其中x 是測試樣本的特征向量，y 是訓練集的。利用這個KNN，在保證整個檢測方案快速啟動的前提下還能確保不會發生誤啟動。第二個KNN 為分類KNN，利用KNN 優秀的分類機制實現線內外故障的區分以及確定故障線路，這個KNN 也是整個檢測方案的主體部分。

本文搭建兩個KNN 模型，這兩個KNN 模型的基本參數相同。考慮到特征數據的差異性，本研究的KNN 模型采用“Mahalanobis”距離函數，該函數能夠考慮到各種特征量之間的聯系并準確提取變量間的微小變化。考慮到不同的k 值對訓練結果具有不同的影響，表1 顯示了兩個KNN 模型中不同k 值的訓練結果。在HVDC 系統中，兩個KNN 模型對k 值的敏感度一致，其訓練和測試數據精度都是隨著k 值的增加而減少，因此本文中兩個KNN 模型的k 值都取1。兩個KNN 模型之間的區別在于類別N 的取值不同。對于判斷KNN，將N 值取為2 以確定它是否是接地故障。對于分類KNN，N 值取4用以實現故障部分和故障線路檢測。

1.3 啟動組件和采樣窗口

在本文研究中，直流電壓差du/dt 直接用于故障檢測的啟動標準。然而，包括電壓導數方法在內傳統方法存在諸如負載波動導致檢測系統誤激活的缺陷。因此KNN 方法在啟動根據DC 電壓差提取電壓波形，然后再使用訓練完的KNN 來確定它是否為接地故障或雙極短路故障。

采樣時間窗口的選擇將嚴重影響整個檢測方案的性能，故障條件下檢測到更長的波形意味著不同區域故障之間的差異更加明顯，所以波形采樣窗口應盡可能長。但是瞬時性是電力系統故障保護的重要因素，這就要求采樣窗口盡可能短。本文通過PSCAD/EMTDC 在不同故障距離和因素下進行模擬，在采樣頻率為10 kHz 的條件下選擇100 個采樣點（10 ms）作為采樣窗口。對于交流側故障，這個采樣窗口可以采集到5 個周期的故障波形。對于線路故障，在輸電線路全長為800 km 假設行波波速為2.95×108m/s 的情況下，該采樣窗口足以采集故障行波在輸電線路上兩個來回的信息。傳統的保護方案采樣窗口基本都有周期時間延遲，而不少新提出的方案采樣窗口也都在5 ms 以上［11-12］。本文所提出的檢測方案采樣窗口為整流側檢測裝置檢測到電壓突變電的前19 個采樣點以及后80 個采樣點，在確保保護精度的前提下更符合故障保護瞬時性的要求。

表1 不同k 值對訓練效果的影響 %

通過PSCAD/EMTDC 在不同故障區域和條件下進行模擬，采集整流側的故障電壓波形，這些一維特征波形就是KNN 的訓練樣本和測試樣本。瞬時性是故障檢測算法的基本要求。研究用的計算機處理器RAM 和處理系統分別為4.00GB 和IntelcoreTM i5-3230 CPU ＠ 2.60GHZ。整個故障檢測算法的啟動組件運行時間為0.038 1 s，KNN 分類程序運行時間為0.041 0 s，完全滿足故障檢測瞬時性的要求。

2 對比方法

為了和KNN 方法進行最直接的比較，借鑒Kong 等［11］提出的方法，將反向行波應用于HVDC 故障檢測。線路外部故障的行波示意圖如圖3 所示，M 代表線路整流側，N 代表逆變側。輸電系統整流側外部發生故障的行波傳播過程如圖3（a）所示，在時間間隔［t0，t0+2l/v］內，線路內部只存在前向行波uf，而反向行波ub=0。因此整流側檢測裝置采集到的電壓信號仍然維持平穩。如圖3（b）所示，當逆變側外部發生故障時，整流側檢測裝置采集到的初始行波是從逆變側傳導過來的反向行波ub。因此，在時間間隔［t0，t0+2l/v］內，檢測裝置能夠檢測到一個突降的反向行波。

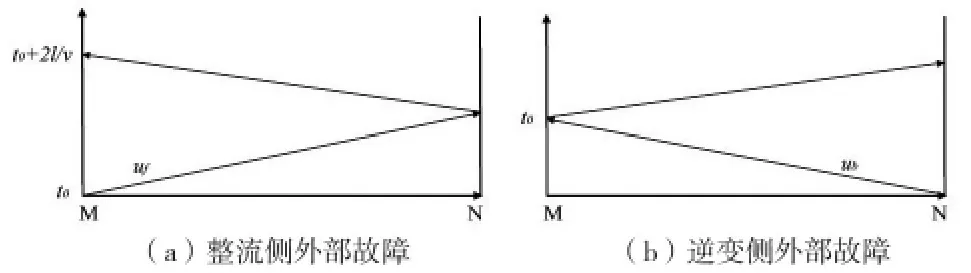
圖3 線路外部故障行波示意圖

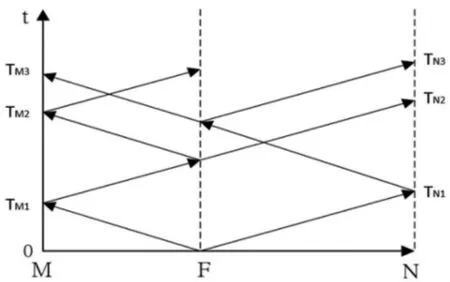
圖4 線路內部故障行波示意圖

線路內部故障的行波示意圖如圖4 所示。在時間間隔［t0，t0+2l/v］內整流側檢測裝置能夠多次檢測到不同行波波頭，如圖中TM1、TM2、TM3…。由于極短時間內不同波頭的抵達，檢測到的故障電壓含有高頻震蕩分量。這使得線路內部故障與線路外部故障存在顯著差異。

當檢測到線路內部故障后，反向行波法利用采集到的電壓故障分量的數字特性識別故障線路。當正極線路短路時，故障點可視為一個對地的負電源，它將造成的整流側電壓Δu＜0。而對于負極接地故障，整流測正極采集到的電壓震蕩且無法保持Δu 負極性穩定。

3 仿真系統和實驗結果

3.1 仿真模型和參數

利用PSCAD/EMTDC 電磁暫態仿真軟件建立仿真模型。本研究基于PSCAD/ EMTDC 中提供的CIGRE 基準模型，建立了標稱電壓為500 kV、額定傳輸功率為1000 MW 的HVDC 輸電系統。一般通用的高壓直流系統的單線結構如圖5 所示［16］。

在該模型中，每個轉換器都有兩組12 脈動轉換器，整流側控制系統采用定電流控制和最小觸發角控制，逆變側控制系統采用定熄弧角控制、定電流控制和電流偏差控制，整流側和逆變側都裝有抵押限流控制VDCOL（Voltage Dependent Current Order Limiter）。系統和變壓器詳細參數見表2 和表3。

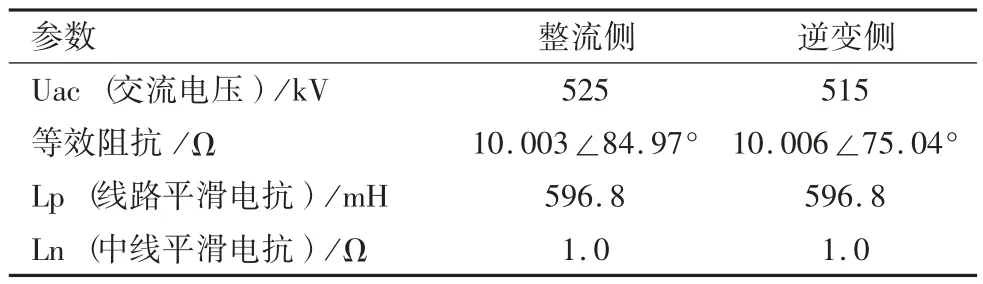
表2 高壓直流輸電系統詳細參數

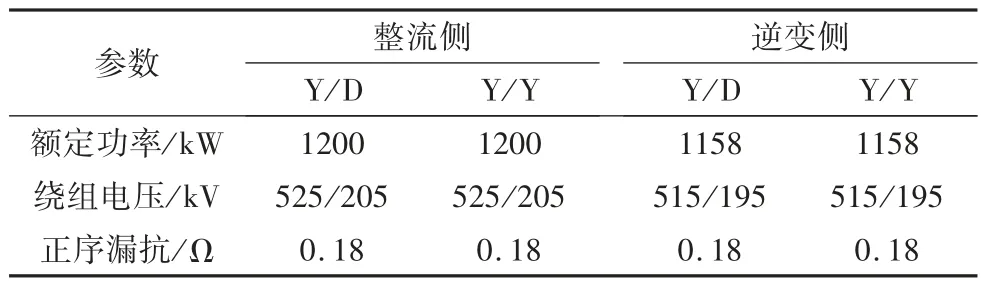
表3 變壓器詳細參數

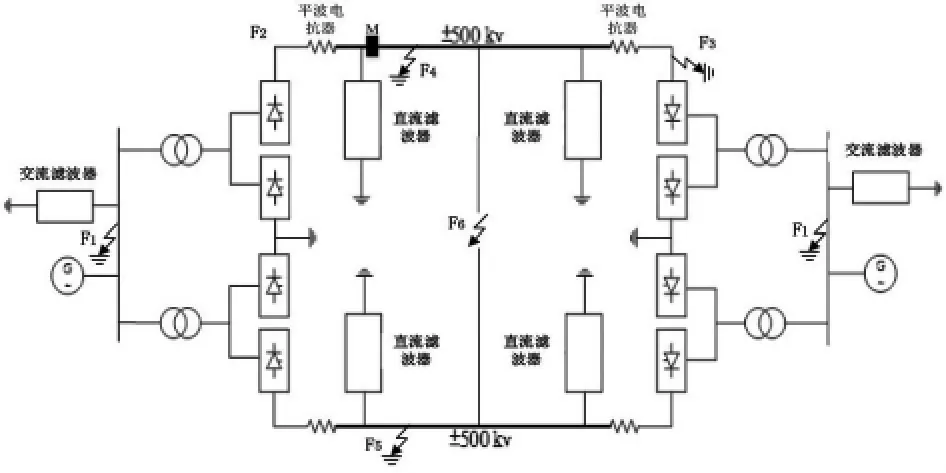
圖5 高壓直流輸電系統單線結構圖

3.2 故障區域仿真

故障檢測實驗是在不同的故障條件和因素下進行的，包括不同的區域、不同的接地電阻和不同的輸電線路。通過整流側檢測裝置M 收集故障發生后的前半周期（100 個采樣點）電壓波形。

HVDC 輸電系統中只有兩條傳輸線，因此線路故障的類型不像交流系統那樣多樣化，單線接地故障（正接地，負接地）最為常見［15］。雙極輸電線路短路故障較為少見并且很難識別［25］。如圖5 所示，將HVDC 系統的故障區域和類型劃分為F1-F6：整流側交流系統接地故障，逆變器側交流系統接地故障，整流器端口故障，逆變器端口故障，正極輸電線路接地故障，負極輸電線路接地故障和雙極短路故障。其中，F1-F3為線路外部故障，雙端交流系統故障統一為交流系統故障。交流系統故障設置為單相接地故障。HVDC 系統不同區域的故障模擬結果如圖6 所示，故障時間設定為1.0 s。

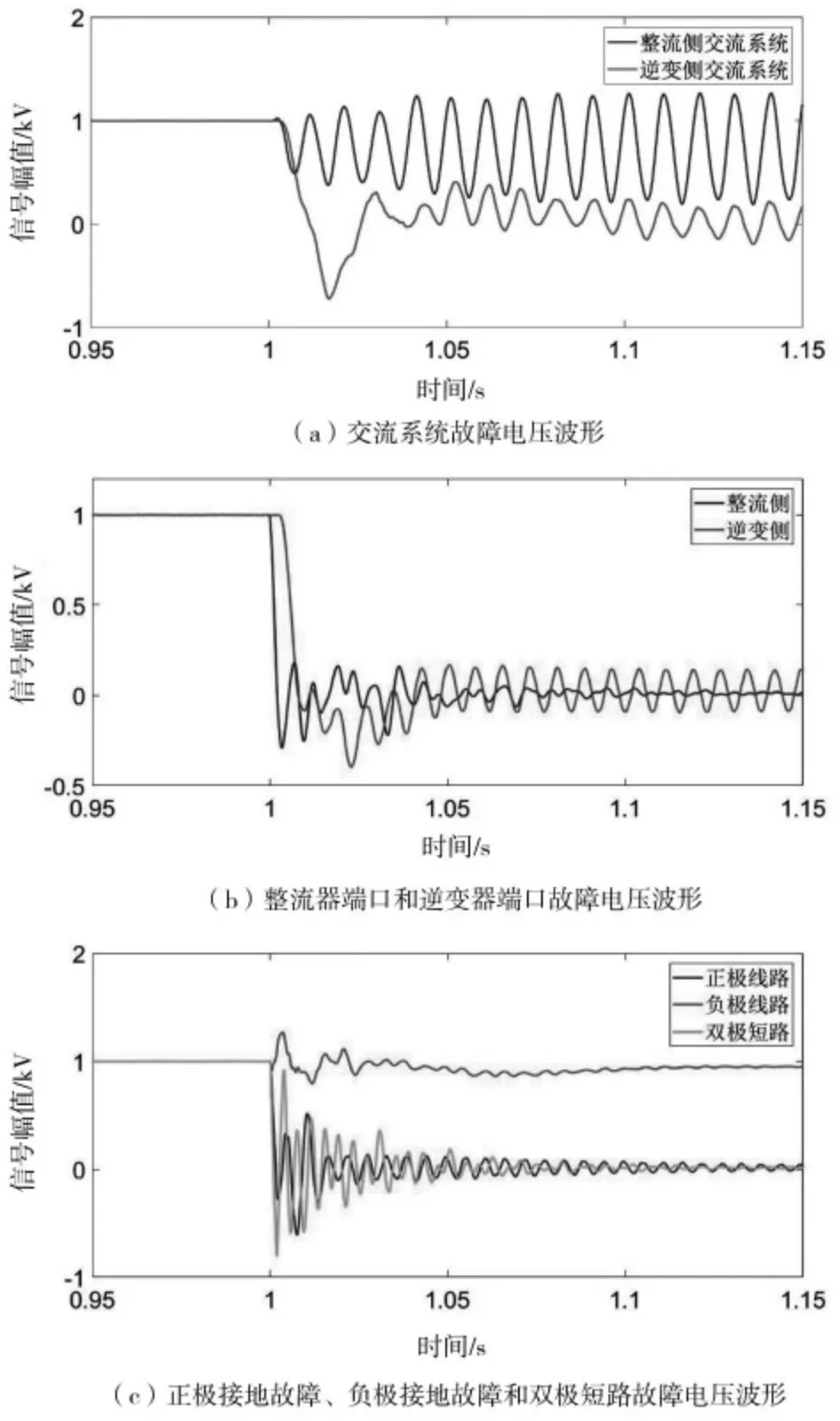
圖6 HVDC 系統不同區域故障仿真

圖6（a）為整流側和逆變側的交流系統故障電壓波形。故障類型為A 相金屬接地。整流器側的電壓波動幅度大于逆變器側的電壓波動幅度，但兩者的電壓波動范圍不是很大。圖6（b）表示在整流器和逆變器端口中發生接地故障之后的電壓波形。與交流系統故障的小幅波動不同，整流器或逆變器發生故障會導致電壓急劇下降。圖6（c）是輸電線路內三種不同故障類型的電壓波形。故障類型皆為金屬接地故障。可以看出，輸電線路內部和外部故障波形完全不同，它會導致電壓大幅度波動并且波動頻率很高。

3.3 訓練數據

在PSCAD/EMTDC 電磁暫態仿真軟件中，整流側檢測裝置采集到故障電壓波形（突變點前19 個采樣點和后80 個采樣點）。這些故障波形直接作為KNN 模型的訓練樣本和測試樣本。

考慮高壓直流輸電系統故障影響因素和區域的多樣性，本文在HVDC 系統6 個區域（F1-F6）分別設置了0～1 000 Ω 的故障接地電阻。基于KNN 小樣本訓練的優越特性，每個區域共設置30 筆故障。KNN 判斷器訓練集共包含2 個種類，每個種類包含180 筆數據，而KNN 分類器包含4 個種類，每個種類包含30 筆數據。本文所設置的故障接地電阻從低到高涵蓋不同阻值范圍，并且對HVDC 所分割的6 個故障區域涵蓋系統的所有元件，保證了訓練樣本的廣度和深度。

3.4 測試數據

為了驗證本文提出的基于KNN 方法以及基于反向行波法的準確性，測試實驗的數據集考慮了不同于KNN 的訓練樣本。本文將故障電阻小于200 Ω 的故障類型歸為低阻接地故障，將故障電阻大于200 Ω 的故障類型歸為高阻接地故障。

為了更好的展現各個方法的性能，本文引入準確度（φ），其計算方法如下：

表4 和表5 顯示了低阻接地故障和高阻接地故障情況下兩種方法的測試結果。“Fault section”表示線內故障和線外故障，Fx 表示故障區域，“Sample number”表示在每個故障區域中測試的樣本數。由于反向行波法無法準確檢測雙極短路故障，因此測試實驗忽略此項目。

表4 低阻接地故障檢測結果

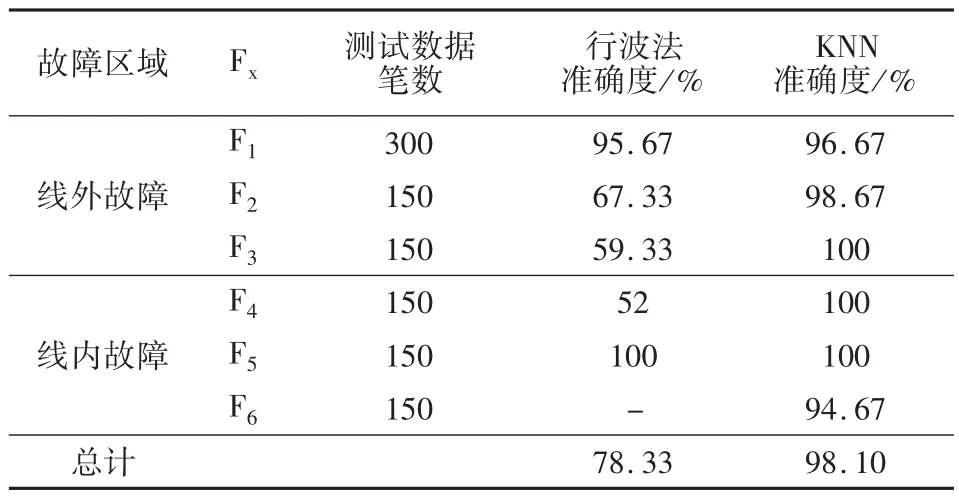
表5 高阻接地故障檢測結果

測試結果表明，反向行波法在低阻故障情況下具有極其優秀的檢測能力，檢測精度甚至超過基于KNN 的故障檢測法，但是在高阻故障情況下它的檢測精度并不理想。這是由于隨著故障電阻的增加，行波波頭將變得難以獲取，這也是行波法的通病。反觀KNN，無論是低阻接地還是高阻接地故障，基于KNN 的檢測方法都具有良好的識別能力。雖然該方法可能會產生輕微誤判，但它們的準確性仍然足以滿足實際工程應用的要求。因此，基于KNN 的故障檢測方法可以實現1 500 Ω以內的故障電阻識別。

3.5 抗干擾測試

電力系統正常運行時，負荷、發電機和調節系統的變化經常會造成系統電壓不同程度的擾動，為了使仿真實驗更貼近實際工程，本節在模型中引入2%、5%兩種不同程度的基準電壓擾動，并測試在這兩種干擾信號下，基于KNN 故障檢測方法的抗干擾特性。實驗結果如表6。

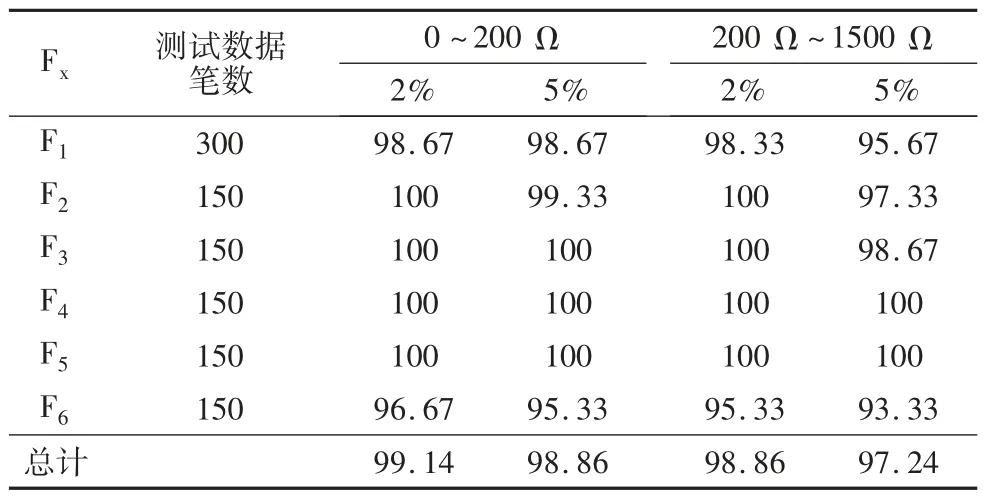
表6 KNN 方法抗干擾測試 準確度（%）

可以看出不論在何種擾動情況下，基于KNN 的故障檢測方法都能保持一個極高的檢測準確精度。即使擾動水平達到5%基準電壓，故障電阻達到1 500 Ω，所提出的方法的檢測準確率仍達到97.24%，這完全滿足實際工程的要求。

高壓直流輸電系統穩定運行時會存在微小干擾信號（視具體線路而定），但干擾達到甚至超過5%基準電壓水平的情況微乎其微。因此基于KNN 的故障檢測方法具有極高的抗干擾穩定性。

3.6 線路故障檢測

在電力系統故障檢測方案中，能否確保輸電線路全長的準確檢測是一個關鍵的評判因素。為了驗證該方法的可靠性，在全長800 km 的輸電線路上，分別在0.1 km 到799.9 km 之間設置不同故障類型，測試結果如表7 所示。表7 的結果表明，即使故障距離發生變化，該方法也能確保輸電線路全長的準確故障識別。

表7 不同輸電線路距離的故障檢測結果

3.7 討論

從上述測試結果可以看出不論是低阻故障還是高阻故障，本文所提出的基于KNN 的故障檢測方法都具有優秀的識別精度且優于傳統行波法。該方法有效提升高壓直流輸電系統故障接地電阻的測量范圍，不論在什么故障區域、條件下，都能夠實現1500 Ω 故障的準確可靠識別，并且通過抗干擾性分析驗證了本方法具有較高的穩定性。

從表5 中可以看出當故障電阻達到一定程度后，傳統行波法將產生較大誤判。這是由于隨故障電阻升高，不同區域的電壓波形變化幅度將減小。以200 Ω 接地故障為例，如圖7 所示。圖7（a）為線路外部區域故障電壓波形，圖7（b）為線路內部故障電壓波形。按照Kong 等［11］提出的反向行波法很難通過設置閾值等方式區分逆變側端口故障或者負極短路故障，并且由于負極短路故障和雙極短路故障的電壓波形極為相近，因此反向行波法也很難識別雙極短路故障。而KNN 能夠通過對距離函數、k 值的選取使得模型對各個故障類別具有優秀的分類能力。只要確保訓練樣本的代表性，基于KNN 的故障檢測方法可以實現大電阻接地的準確檢測。

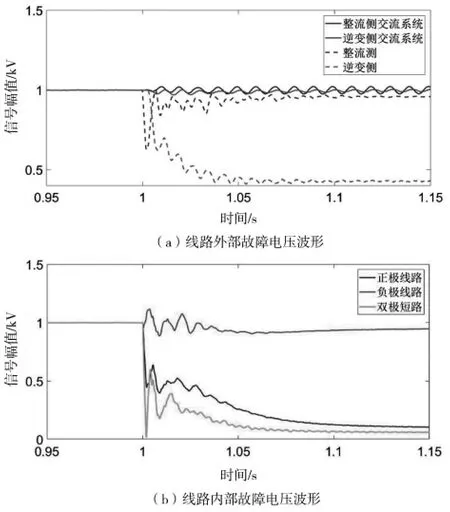
圖7 高阻故障條件下不同區域電壓波形

4 結論

本文提出的基于K-最近鄰的HVDC 單端故障檢測方法，可以準確檢測HVDC 輸電系統中的高阻故障的區域和線路，整流側采集的故障電壓用于所提出的KNN 模型的訓練數據。訓練后的KNN 模型用于檢測故障區域。還列出了基于反向行波的故障檢測方法解決上述問題。通過PSCAD/EMTDC 軟件進行仿真，驗證兩種方法的可行性。測試結果表明，相比方向行波法，基于KNN 的高壓直流輸電系統故障檢測方法可以提高故障檢測性能并實現故障電阻高達1 500 Ω 的特殊故障區域的準確檢測。