基于Recurdyn 的某無人平臺懸架系統優化設計

吳 天，任志英，劉 巖，鄭文彬

（1.福州大學機械工程學院，福建 福州 350000；2.新鄉北方車輛儀表有限公司，河南 新鄉 453000）

1 引言

無人平臺系指無人駕駛的、完全由遙控操作或者按預編程序自主運作的平臺。就目前而言，大致包括為無人作戰平臺與無人運輸平臺。因無人平臺在設計時無需考慮人的因素及其相關的設備，成本低廉，全壽命費用大為減少。無人平臺是近幾年新出現的概念，國外提出發展無人平臺都是有明確的需求背景的，如考慮到未來局部戰爭等環境十分嚴峻的戰場，各種高新技術武器裝備充斥在其中，命中精度高、機動性強、射程遠、殺傷威力大等，這對交戰雙方都構成極大的威脅。如何以最小的損失以及人員傷亡取得最大的戰果，這是各國軍事作戰部門優先關注的問題。此外，各國在發展新武器裝備時都面臨著預算日趨拮據而裝備費用日趨上漲的困境，如何謀求經濟上能負擔得起的高效費比武器裝備也成為各國優先考慮的需要。除此之外搶險救災上無人平臺也可提供強有力的支援，減少人力消耗以及事故中人員傷亡。

底盤懸架對于無人平臺是極為重要的組成部分，它具有承載、傳力（矩）、緩沖、衰振、散能以及調節平臺高度等主要功能，對保護平臺中的精密儀器有巨大作用。而懸架空間結構復雜，傳統設計分析方法難度大，效率低，通過改變懸架設計硬點參數是一種優化懸架特性的有效方法，但是如果考慮多個定位參數之間的相互影響，通過大量設計參數相互權衡得到理想的特性十分困難，因此懸架的設計是一個復雜的多目標優化問題[1]。Recurdyn/AutoDesign 模塊是一個集DOE、元模型（MetaModel）技術和數值優化技術為一體的自動化設計優化工具，幾乎采用最小的采樣點構建初始元模型，在優化過程中，通過自動地提高元模型的保真度，克服了由于數據不足而引起的數值奇異，從而避免了優化過程的分析失敗[2]。基于Recurdyn 對雙橫臂式懸掛系統進行建模和仿真，分析評價其性能，再對懸架定位參數進行優化，對于懸架設計具有一定指導作用。

2 無人平臺以及懸架模型

此次選擇的是一噸級6×6 多功能無人平臺，采用全電動底盤，六電機分布式驅動，具備全地形通過、多模式人機交互、高可靠通信等性能，可實現目標潛伏偵察、陣地全景觀測、物資自主運輸等。其中平臺質量800kg，載重質量400kg，最大速度30km/h，無人平臺實物，如圖1 所示。

無人平臺在執行特殊任務時所搭載的任務單元需要減振緩沖，且通過性能要好，因此平臺對于懸架有較高的要求。綜上考慮多方面因素，選擇雙橫臂式懸架，雙橫臂式獨立懸架擁有橫向剛度大、抗側傾性能優異、抓地性能好等特性。按上下橫臂是否等長，可分為等長雙橫臂式和不等長雙橫臂式兩種懸架。等長雙橫臂式懸架在車輪上下跳動時，能保持主銷傾角不變，但輪距變化大，造成輪胎磨損嚴重，現已很少用。對于不等長雙橫臂式懸架，只要適當選擇、優化上下橫臂的長度，并通過合理的布置、就可以使輪距及前輪定位參數變化均在可接受的限定范圍內，保證平臺具有良好的運動穩定性，從而保護所搭載的任務單元。典型的雙橫臂懸架系統由5 個部分組成：上擺臂、下擺臂、拉桿、轉向節、阻尼減震器和輪胎。上下擺臂為非等長結構，通過轉動副與車架相連接，轉向節通過球鉸與上下擺臂以及轉向橫拉桿連接，轉向橫拉桿再與車架通過球鉸連接[3]，如圖2 所示。

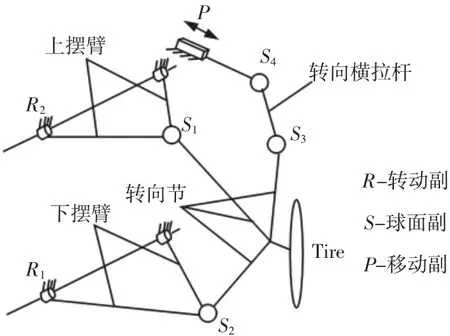
圖2 雙橫臂懸架簡圖Fig.2 Sketch of Double Wishbone Suspension

雙橫臂懸架系統模型的自由度F=5×6－4×3－2×5－1×6=2，即車輪繞主銷的旋轉和車輪垂直跳動兩個自由度。硬點的空間位置坐標是建立運動模型的關鍵，首先在Solidworks 中使用測量工具測量關鍵硬點的參數，而后在Recurdyn 中建立參數點、設計變量，參數點位置，如圖3 所示。A、B、C點分別為下擺臂前、后、外支點；E、F、D分別為上擺臂前、后、外支點，G、H分別為轉向橫拉桿外、內支點。懸架實物，如圖4 所示。

圖3 Recurdyn 后懸架仿真模型Fig.3 Rear Suspension Simulation Model in Recurdyn

圖4 懸架Fig.4 Suspension

3 設計優化

3.1 設計變量選擇

表1 設計變量參數Tab.1 Parameters of Design Variables

綜上所知，所選硬點共8 個，以各個硬點的X、Y、Z三個坐標作為設計變量，共得到24 個設計變量，如表1 所示。表1 所提供的坐標數據已坐標變換，下擺臂AB中點為坐標原點[4]。

3.2 目標函數設計

目標函數是為了找出滿足其功能性或其他要求的可接受的設計，滿足整個設計約束的可接受設計稱為可行性設計，優化中會有多個可接受設計，為了找出最優方案，必須通過一個準則進行判別優劣，該準則一般表示為設計變量的函數[5]。此次優化為多目標優化，因為選擇的無人平臺屬于低速平臺，轉向方式為差速中心轉向，且各點變化范圍很小，對主銷內傾角與主銷后傾角影響不會太大，故暫不考慮主銷內傾角與主銷后傾角，只考慮前束角與輪胎外傾角。我們目的是減小前束角和外傾角振動范圍。Recurdyn 不能直接提供這些值，因此要通過使用表達式（Expression）和變量方程（Variable Equation）來進行計算，為此，可以先得到前束角和外傾角的最小值和最大值。這樣，最大值與最小值之間的差值就是其振動范圍，則優化問題就是要減小前束角（AR1）和外傾角（AR2）在輪胎跳動時的振動幅值。

3.3 設計指標制定

確定目標函數后，設置約束條件，范圍要小于優化前的值，默認權重比為1，如圖5 所示。設計問題定義為MinF1和MinF2，約束條件為R1≤C1，R2≤C2，因為目標優化的質量取決于初始樣本的數量，而這里的問題有24 個設計變量，這需要非常多的采樣點，但這兩個不等式約束可以避免未成熟收斂。則設計指標的計算方法為：

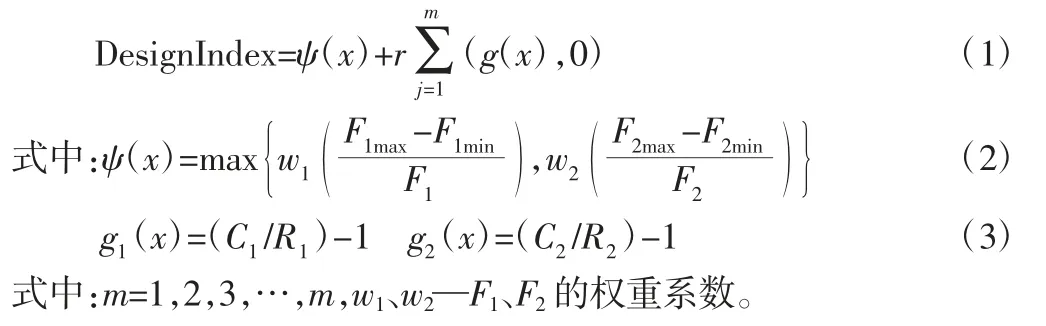
圖5 目標函數約束設置Fig.5 Setting of Objective Function Constraint

3.4 DOE 分析

設計研究的主要目的是分析各個設計變量的變化對系統性能的影響、設計變量的最佳取值以及系統性能對設計變量變化的敏感程度。DOE 是安排試驗和分析試驗數據的數理統計方法，主要是進行合理的安排試驗，用很小的試驗規模、較短的周期以及較低的試驗成本，通過試驗設計，能夠考慮再多個設計變量同時發生變化時，各個變量對系統目標性能的影響[6]。基于Recurdyn軟件環境的設計研究包含了靈敏度分析及設計變量篩選，提供多種試驗設計方法，如三水平正交設計等[7]。由于選擇變量的個數是24，如果選擇3-Level Orthogonal Array 需要進行52 次試驗，為減少試驗次數，選擇2-Level Orthogonal Array，只需要32 次試驗，且優化結果相差較小。各個變量分別對目標函數1（前束角變化）與目標函數2（外傾角變化）的敏感程度，如圖6 所示。

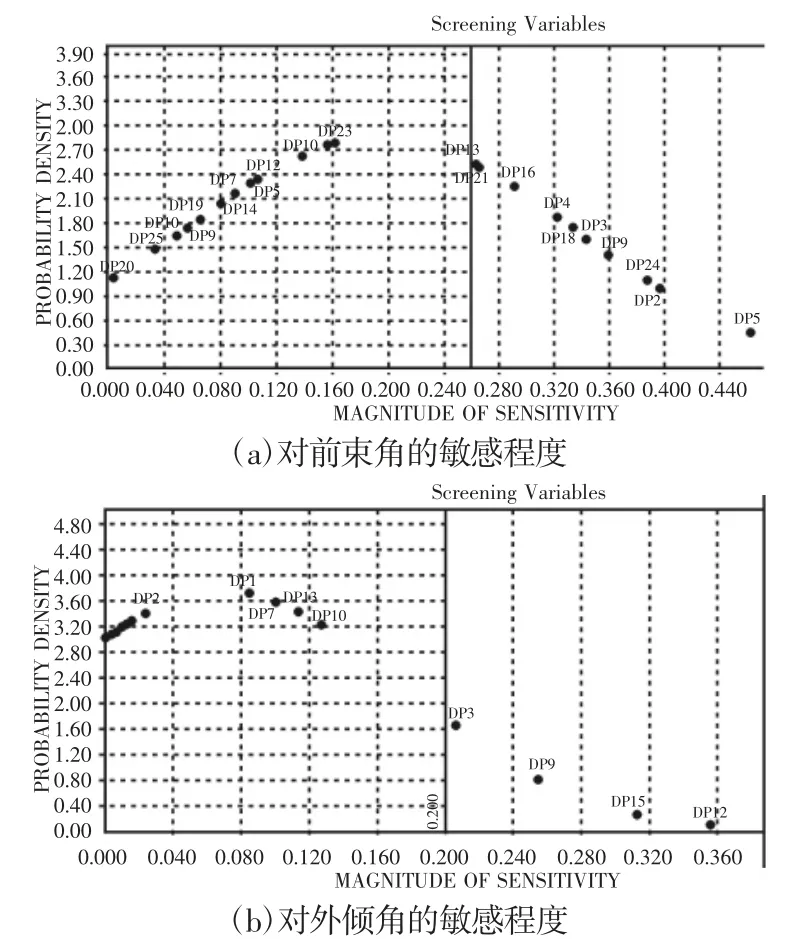
圖6 設計變量DOE 分析圖Fig.6 DOE Diagram of Design Variables

由圖可知，右邊位置的點比左邊的點更加敏感，對于目標函數1 設置的截止值（Cutoff Value）是0.26，目標函數2 設置為0.2，最后篩選出的設計變量共12 個，如圖7 所示。大多數的有效設計參數是Z軸的值。在Recurdyn 中用于元模型的DOE 方法有FC中心復合設計（CCD）、經典二次響應面模型法（BBD）等5 種，元模型的初始DOE 選擇方法，如圖8 所示。當前設計在中心位置的50%范圍內，建議使用ISCD-1 或ISCD-2，并且此方法還能縮小取樣數，其中，ISCD-2 一般用于設計優化，ISCD-1 用于DFSS/穩健設計優化。由此可得此次設計選擇的初始DOE 法為ISCD-2（Incomplete Small Composite Design-ll），如圖9 所示。

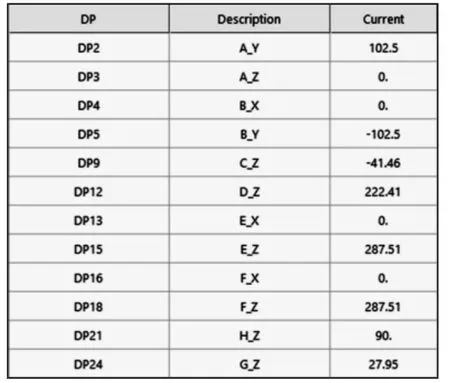
圖7 篩選出的設計變量Fig.7 Screened Design Variables

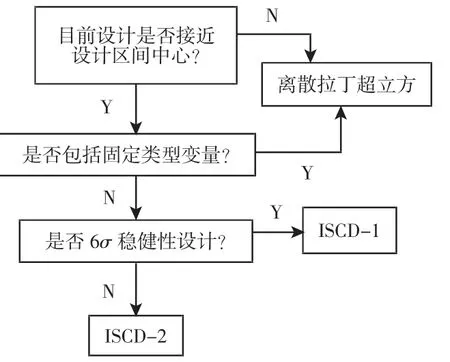
圖8 DOE 選擇方法Fig.8 The Selection of DOE Method

圖9 ISCD-2Fig.9 Incomplete Small Composite Design-ll

3.5 元模型（Meta-Model）方法選擇

Recurdyn 的元模型方法包括了協同克拉格法、徑向基函數法、保守響應面法以及多項式函數法，選擇方法，如圖10 所示。綜上可得，元模型方法選擇MQ 徑向基函數法。徑向基函數（RBF）是用于插值目的的一類函數，其處理多元函數逼近問題具有效率高，運算簡單，不依賴于網格，求解精度高等優點。它們的值只取決于一般點和特定函數中心之間的距離[8]。RBF 法利用徑向基函數Bi（x）和多項式基函數Xj（x）構造了逼近所有采樣點的近似函數y（x）[9]。近似函數y（x）的描述如下：

由于距離是標量值，矩陣B是對稱矩陣，因此，如果矩陣B的逆存在，則保證了唯一解[10]。

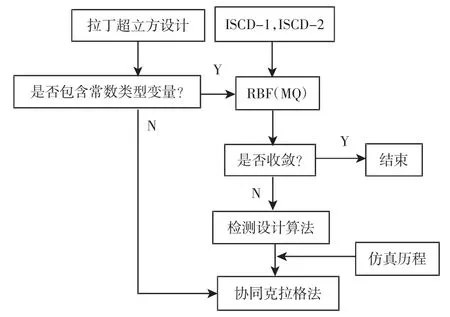
圖10 元模型的選擇方法Fig.10 The Selection of Meta-Model Method

4 優化結果分析

4.1 優化結果

優化結束后，可得到收斂歷程以及優化結果，如圖11 所示。優化過程僅在第16 個迭代步便收斂。整個優化過程共32 次計算，包括17 次初始采樣點分析。優化后各點取值，如表2 所示。兩個響應目標AR1 和AR2 在最優解時取值分別為0.14、0.52，如表3 所示。

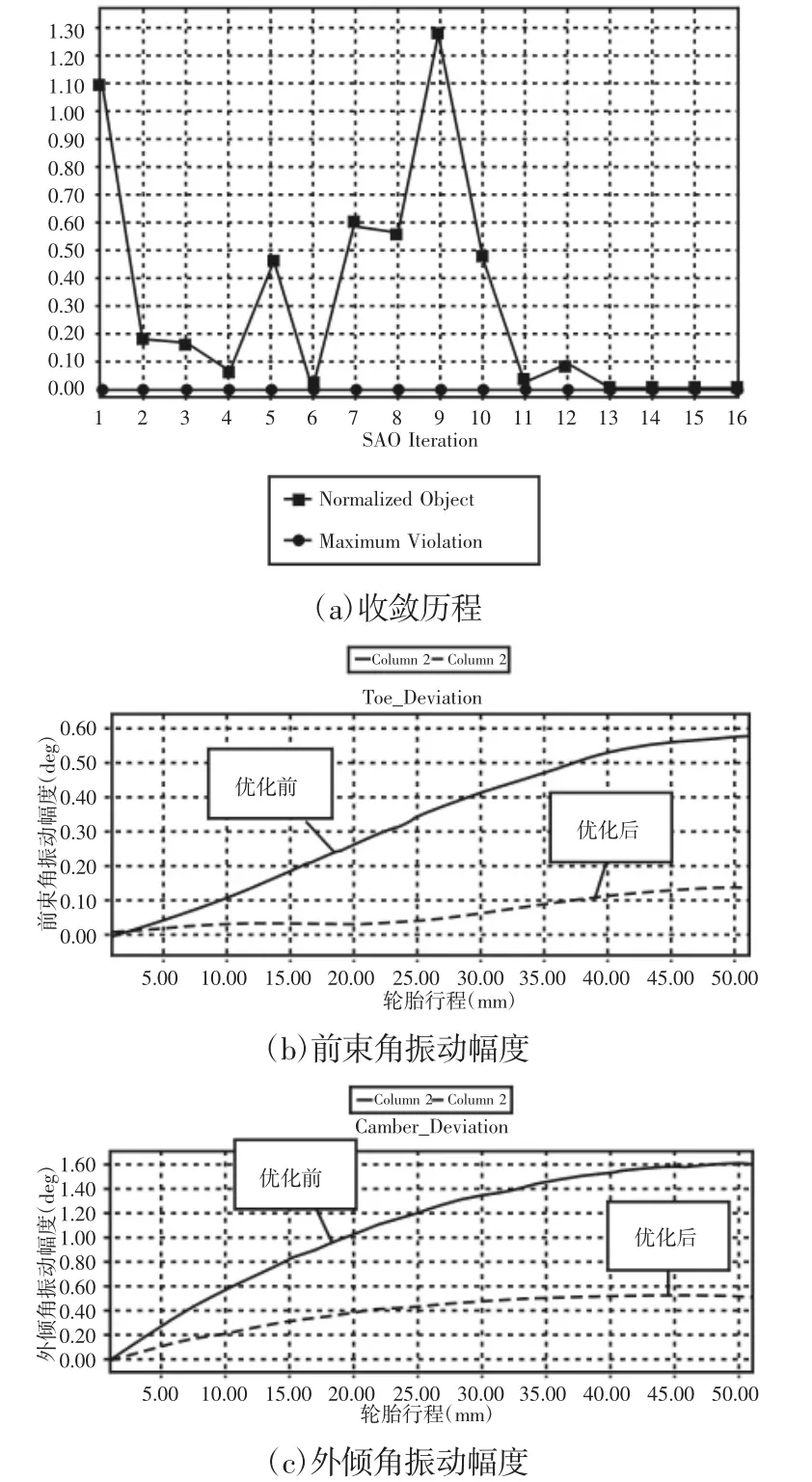
圖11 優化結果Fig.11 Optimization Results

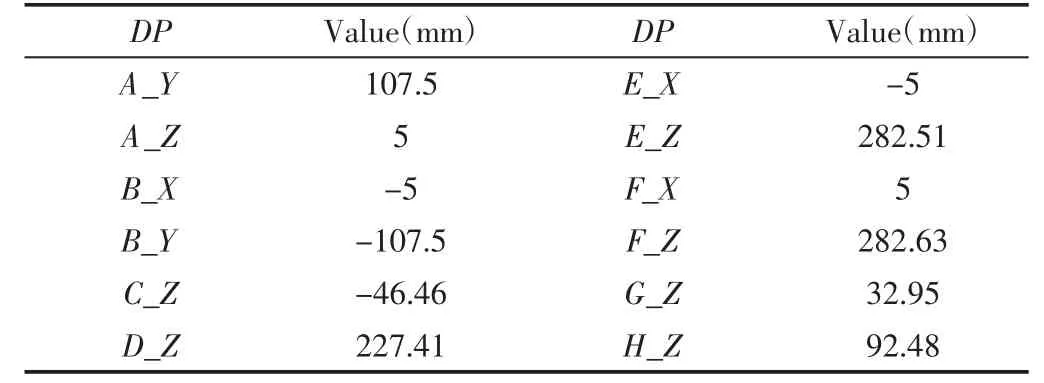
表2 優化后定位參數取值Tab.2 Values of Parameters After Optimization

表3 定位參數優化結果Tab.3 Parameter Optimization Results

4.2 結果分析

由以上結果可知，優化后的數據與優化前的0.58、1.60 相比減少很多，表明在優化后各個車輪在垂直跳動時前束角與外傾角變化數值更小，運動也更加平穩。變化范圍，如表4 所示。在車輪的整個跳動范圍內。優化后的無人平臺過0.1m 起伏路面時車體垂向加速度，如圖12 所示。綜上所述，優化結果較好地滿足了懸架的設計要求，適用于雙橫臂式懸架系統的結構優化。

表4 定位參數變化范圍Tab.4 The Variation Range of the Parameters

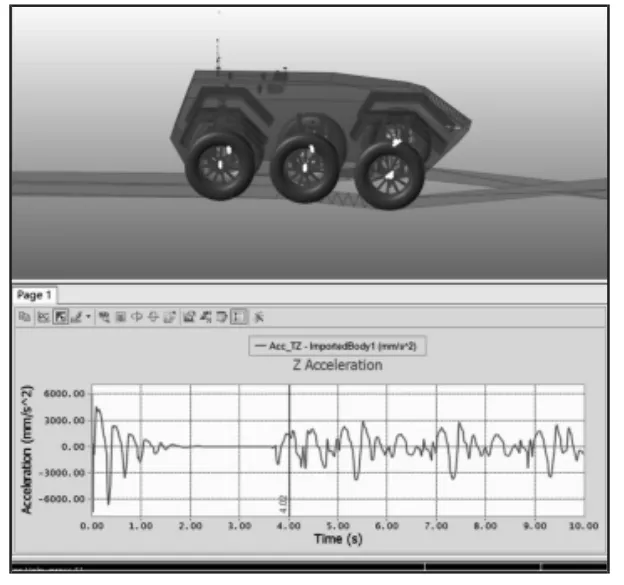
圖12 過起伏路面時車體垂向加速度Fig.12 Vertical Acceleration of Vehicle Body over Polyline Road

5 結論

經過優化設計使得平臺懸架穩定性能與減震緩沖性能有明顯的提升，進而也提高了其自主控制過程中的路徑跟蹤精度與規劃能力。應用Recurdyn 仿真軟件可以使懸架系統的研發變的更加高效、便捷，大量縮短開發周期，減少研發成本，通過選擇適當的優化方法可較好地實現懸架性能的優化。除此之外，提出的方法經過適當改進可用于其他類型的懸架系統優化設計。