一類三平移3-RRC 并聯機構的運動學

羅建國，邱杰清，趙韻秋

（1.華北科技學院機電工程學院，北京101601；2.華北科技學院研究生院，北京101601）

1 引言

并聯機構具有剛度較大、結構穩定、誤差小、精度高、易于實現高速運動、結構簡單等優點，使其在某些領域得到廣泛的應用[1]。三平移并聯機構是僅有一個位姿的特殊并聯機構，廣泛應用于精密加工、醫學、微電子、精密測量等精密工程等領域。許多學者對三平移并聯機構進行過研究，并提出了很多不同類型的三平移并聯機構[2-5]。3-RRC 并聯機構是一種結構簡單的并聯機構，在一定結構下可實現三維平移。文獻[6]對一種各支鏈3 運動副軸線平行且對稱的3-RRC 進行了速度和加速度分析，文獻[7-9]分別對一種各支鏈3 運動副軸線平行且3 支鏈相互位置一定的3-RRC 進行了位置分析、特殊位形分析、工作空間分析。

對一類各支鏈3 運動副軸線平行的3-RRC 并聯機構進行了自由度分析、正逆解求解、工作空間求解、奇異位形分析，并給出了簡潔又快速的計算分析方法。

2 結構及坐標系建立

3-RRC 并聯機器人，如圖1 所示。它由三條結構相同的分支及動（上）平臺和靜（下）平臺組成，各支鏈3 運動副軸線平行，并且各支鏈的第一個轉動副和圓柱副分別固定在靜平臺和動平臺上。在靜平臺和動平臺內心處固聯固定坐標系O-XYZ、動坐標系P-xyz，如圖1 所示。使Y軸與轉動副A1的軸線垂直，y軸與圓柱副C1的軸線垂直，Z軸與z軸垂直于靜平臺豎直向上，X軸與x軸由右手迪卡爾坐標系確定方向。設θi為AiBi繞轉動副Ai的軸線逆時針旋轉至與OXY平面平行的轉角，φi為BiCi繞轉動副Bi的軸線逆時針旋轉至與OXY平面平行轉角，OA2、OA3與OA1的夾角分別為δ2、δ3，轉動副Ai和Bi軸線之間的距離為ai，轉動副Bi和Ci軸線之間的距離為bi，動平臺內接圓半徑為r，靜平臺內接圓半徑為R，其中θi、φi由機構的位形決定，ai、bi、r、R、δ2、δ3由機構的結構確定，（i=1、2、3）下同。

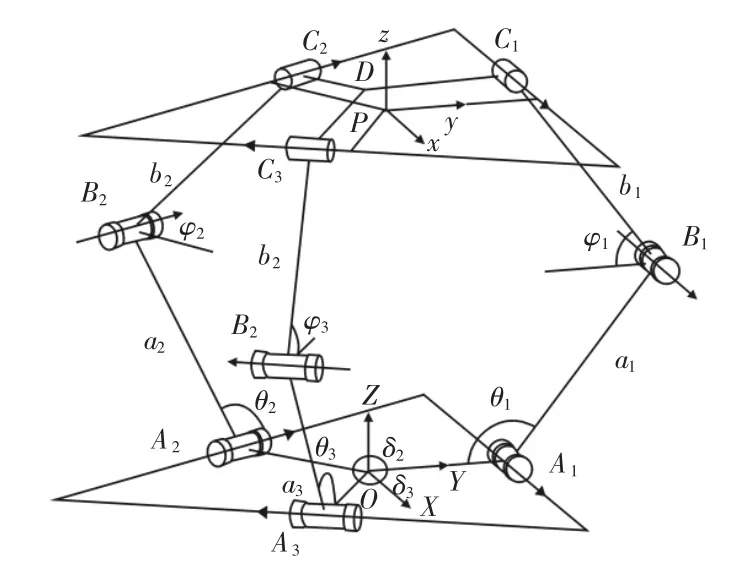
圖1 三平移3-RRC 并聯機構Fig.1 3-DOF Translational 3-RRC Parallel Mechanisms

3 自由度分析

基于螺旋理論（反螺旋）的自由度分析原理和修正的Kutzbach-Grübler 公式求解機構的自由度[10]，該方法不僅可以計算機構的自由度數目還可以通過動平臺約束螺旋系的反螺旋得到動平臺的自由度性質。這里討論的3-RRC 并聯機構在任一位形下，圓柱副C1、C2、C3的軸線都平行于靜平臺，即動平臺與靜平臺平行，在此前提下分別分析各支鏈。在支鏈i的Ai上建立坐標系Ai-xiyizi，如圖2 所示。

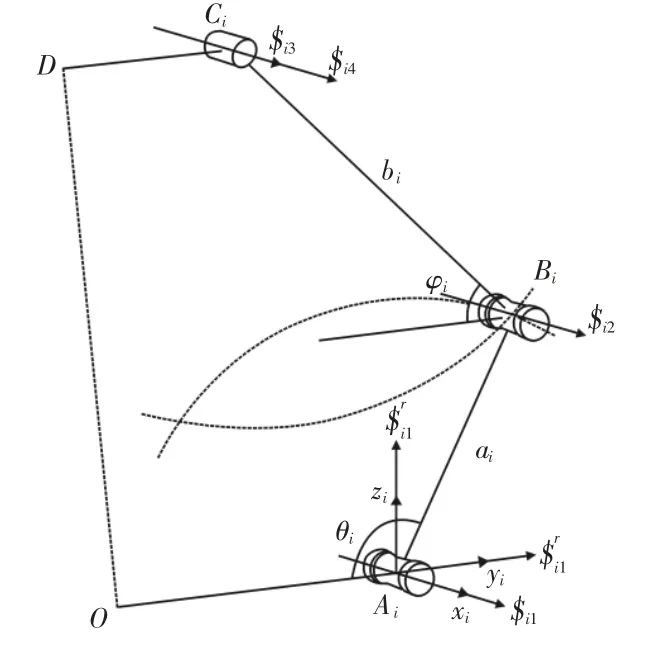
圖2 支鏈結構Fig.2 One RRC Limb

支鏈i對動平臺有2 個約束分別為垂直于動平臺的約束力偶和平行于動平臺的約束力偶。

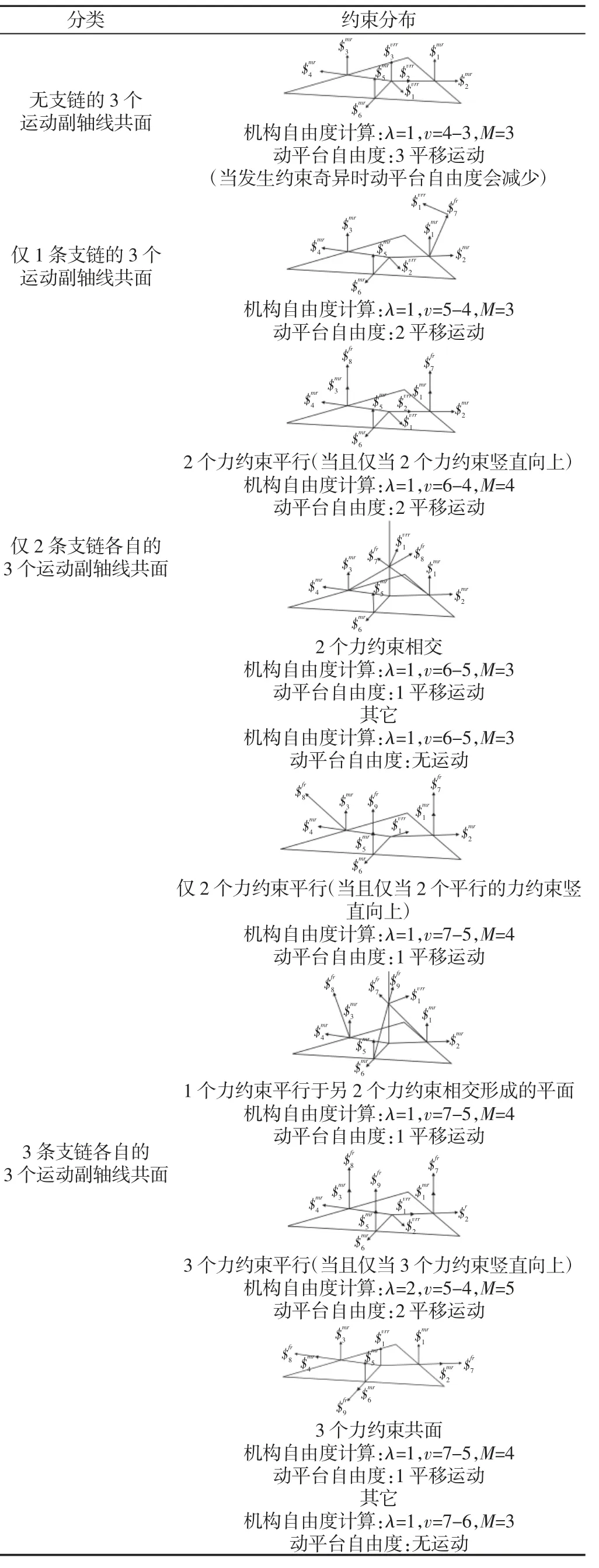
表1 3-RRC 在非約束奇異位形下的自由度Tab.1 DOF of 3-RRC in Unconstrained Singular Configuration

綜上可知，當3 個支鏈各自的3 個運動副軸線都不共面時，3 個支鏈對動平臺有6 個力約束如表1 的第一種情況，其中3 個支鏈都施加了豎直向上的力約束，即公共約束λ=1，去除多余的公共約束后3 個支鏈對動平臺只有3 個獨立的約束，即冗余約束v=4-3=1。再對運動平臺的約束螺旋系求反螺旋得到3 個獨立的移動運動螺旋從而斷定動平臺具有3 平移運動。該機構的自由度可由修正的Kutzbach-Grübler 公式計算，考慮公共約束λ=1 和冗余約束v=1，有：

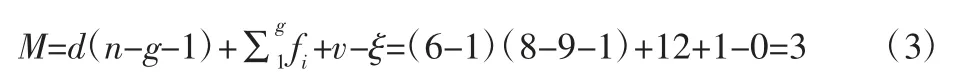
式中：M—機構的自由度；d—機構的“階”由公共約束λ 確定，d=

6-λ；n—包括機架的構件數目；g—運動副的數目；fi—第i個運動副的自由度；v并聯冗余約束；ξ—機構中存在的局部自由度。

假設支鏈i的3 個運動副軸線共面，同理可得到其約束反螺旋系有3 個螺旋為：

對比可知，3 個運動副軸線共面將對動平臺多產生一個過AiBiCi的力約束，從而改變機構自由度和動平臺自由度。分4 種情況分析，如表1 所示。

綜上可知對于并聯機構，當運動到特定位形時，有一條或幾條支鏈上原來獨立的運動螺旋變得線性相關則會在動平臺上引入一個或幾個新的約束螺旋，在新約束螺旋和舊約束螺旋組成的螺旋組中獨立的新約束螺旋數和非獨立的新約束螺旋數分別與動平臺自由度減少數和機構自由度增加數相等。對于這里的3-RRC 并聯機構，當且僅當至少有1 條支鏈的3 個運動副軸線共面時，有支鏈的運動螺旋線性相關必引入獨立的新約束使得動平臺自由度減少，機構處于運動奇異。

4 位置求解

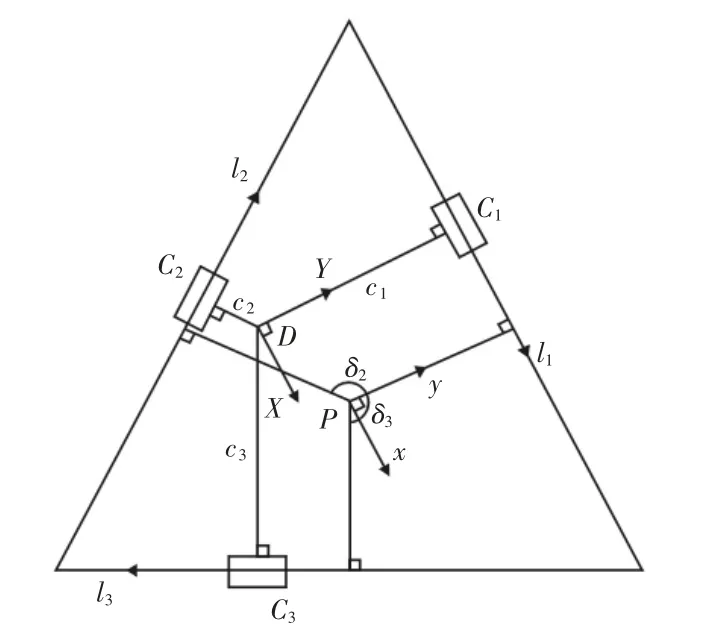
圖3 動平臺俯視圖Fig.3 Top View of Mobile Platform

設動平臺上點P在固定坐標系的位置為（XP，YP，ZP）T，并用Z-Y-X型歐拉角（α，β，γ）T表示動平臺相對于靜平臺的姿態。由于機構處于任一位形下都有圓柱副C1、C2、C3的軸線分別平行于轉動副A1、A2、A3的軸線，從而恒有α=0、β=0、γ=0。動平臺俯視圖，如圖3 所示。DXY為靜平臺OXY在動平臺上的投影，直線l1、l2、l3分別與圓柱副C1、C2、C3的軸線重合，c1、c2、c3分別為D點至C1、C2、C3的位移。在坐標系Oxy中，l1、l2、l3的直線方程及C1、C2、C3的坐標不難得到，再由點到直線的距離公式可求得c1、c2、c3如下：

4.1 位置逆解

位置逆解是當結構參數和動平臺的位姿（XP，YP，ZP，α，β，γ）T給定時，求各支鏈作為輸入的轉動副的轉角或移動副的位移。根據主動副確定準則，以每個支鏈的第一個轉動副作為輸入，即（θ1，θ2，θ3）T。由上面的分析可知這里的3-RRC機構僅有一個姿態，即（α，β，γ）T=（0，0，0）T，所以對于給定的位姿（XP，YP，ZP，α，β，γ）T≠（XP，YP，ZP，0，0，0）T時無解。下面對（XP，YP，ZP，α，β，γ）T=（XP，YP，ZP，0，0，0）T的情景進行求位置逆解。

取支鏈i求解，當XP、YP、ZP給定時可由式（5）可求出ci。在圖2 中Ai-xiyizi坐標系下Ai、Ci坐標分別為Ai（0，0，0）、Ci（0，ci-R，ZP），則Bi為以Ai為圓心ai為半徑的圓Ai與以Ci為圓心bi為半徑的圓Ci的交點，Bi存在即逆解存在，其必要條件為：

二元二次方程組最多可有2 組解，如式（7）所示。每組解可確定唯一θi，可由下式解得：

綜上可知對于這里的3-RRC并聯機構當給定位姿（XP，YP，ZP，α，β，γ）T時，每條支鏈最多可有2 組解，3 條支鏈最多8 組解，即8 種位形。

4.2 位置正解

位置正解是已知結構參數和機構輸入（θ1，θ2，θ3）T時，求動平臺的位姿（XP，YP，ZP，α，β，γ）T。由于討論的3-RRC并聯機構僅有一個姿態，即（α，β，γ）T=（0，0，0）T，所以對于任意輸入（θ1，θ2，θ3）T，動平臺的位姿（XP，YP，ZP，α，β，γ）T=（XP，YP，ZP，0，0，0）T。

當給定（θ1，θ2，θ3）T時，在Ai-xiyizi坐標系下可得Bi（0，-ai Cθi，aiSθi）、Ci（0，ci-R，ZP），Bi、Ci兩點間距離即為bi，可列出如下關系式：

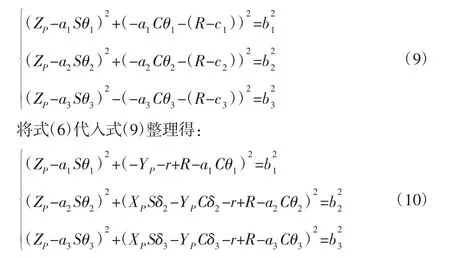
三元二次方程組，最多可有8 組解，如式（10）所示。并且從式（10）可以看出正解為3 個圓柱面的交點，其軸線與半徑分別如下：

（1）軸線方程：Z=a1Sθ1，-Y-r+R-a1Cθ1=0；半徑為b1。

（2）軸線方程：Z=a2Sθ2，XSδ2-YCδ2-r+R-a2Cθ2=0；半徑為b2。

（3）軸線方程：Z=a3Sθ3，XSδ3+YCδ3+r-R+a3Cθ3=0；半徑為b3。

可以用CAD 軟件繪制出對應的3 個圓柱體并求交得到相交體，頂點坐標即為正解。

5 工作空間求解

綜合位置逆解中對3 條支鏈的分析，可知對于給定的動平臺位置（XP，YP，ZP）T有位置逆解的充分必要條件為：當i=1、2、3時，XP、YP、ZP都滿足式（6）。

所有有逆解的（XP，YP，ZP）T構成了這里3-RRC 并聯機構的可達工作空間，其方程如下：

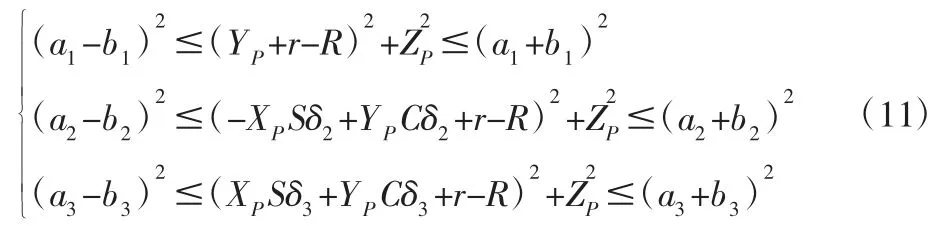
當（XP，YP，ZP）T位于可達工作空間表面時，式（11）至少有1個等號成立，即至少有1 條支鏈的3 個運動副軸線共面，機構剛好處于運動奇異。當至少有1 條支鏈的3 個運動副軸線共面時，式（11）至少有1 個等號成立，（XP，YP，ZP）T剛好位于可達工作空間外表面。所以處于運動奇異的所有位形與（XP，YP，ZP）T位于可達工作空間表面的所有位形一致。

式（12）的解為3 個空心圓柱的交。利用CAD 軟件繪制對應的3 個空心圓柱并求交得到工作空間。

5.1 實例驗證

給出結構參數a1=a2=a3=b1=b2=b3=200mm、r=25mm、R=50mm、δ2=δ3=120°。

將結構參數代入（11）得：

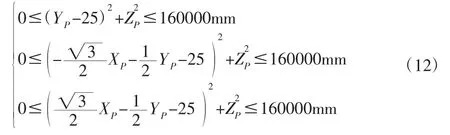
使用Autodesk 公司的AutoCAD 軟件繪制了如圖4（a）的3個圓柱體，并求交得如圖4（b）的對稱實體，即可達工作空間。利用AutoCAD 的查詢功能可得到工作空間實體對象的一些信息，其中體積為290429255.0425mm3，頂點坐標也可得到，如圖4 所示。

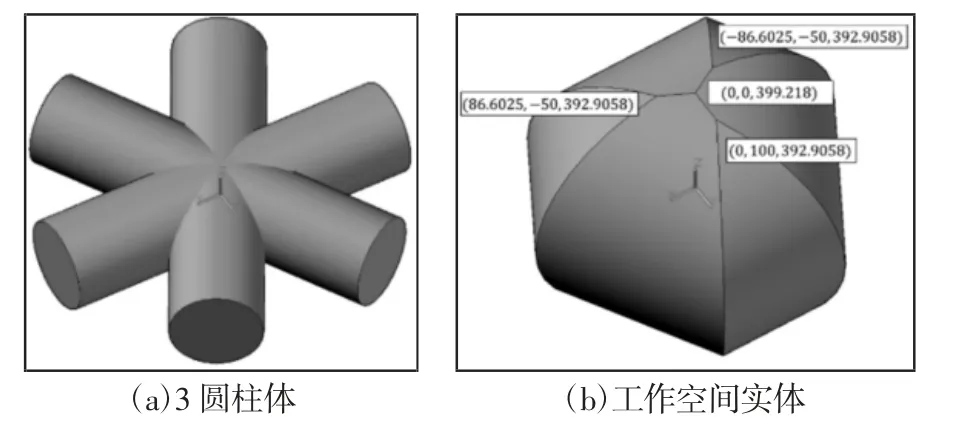
圖4 工作空間求解Fig.4 Workspace Solution

下面對所得工作空間中的點求逆解再求反解以驗證結果的正確性。

取圖4（b）中工作空間的4 個頂點為動平臺P點位置求逆解。已知結構參數，并分別取（XP，YP，ZP）T=（0，0，399.218mm）T、（-86.6025mm，-50mm，392.9058mm）T、（0，100mm，392.9058mm）T、（86.6025mm，-50mm，392.9058mm）T可得逆解，如表2 所示。由于選取了極限位移點逆解僅有一組。

正解計算：

取逆解計算中得到的4 組（θ1，θ2，θ3）T作為正解的輸入。已知結構參數，并分別取（θ1，θ2，θ3）T=（86.4167°，86.4167°，86.4167°）T、（79.1931°，100.1931°，79.1931°）T、（100.1931°，79.1931°，79.1931°）T、（79.1931°，79.1931°，100.1931°）T可得正解，如表2 所示。

可以看出正逆解的計算值非常吻合，并且求得的所有正解仍滿足式（12），驗證了所求工作空間的正確性。

表2 實例位置正逆解 長度單位：mmTab.2 Inverse and Forward Position Solution of the Instance

6 奇異位形分析

按形成原因分奇異可分成2 類[11]：運動奇異、約束奇異。

對于分析的3-RRC 并聯機構的運動奇異已經在自由度分析中給出了產生的條件，即至少有1 條支鏈的3 個運動副軸線共面，并在工作空間分析中給出了處于運動奇異的所有位形。下面分析約束奇異。

鎖住該3-RRC所有的主動件，則獲得一類各支鏈3 運動副軸線平行的3-RC并聯機構，如表3 所示。做出其動平臺約束分布圖并進行自由度分析。

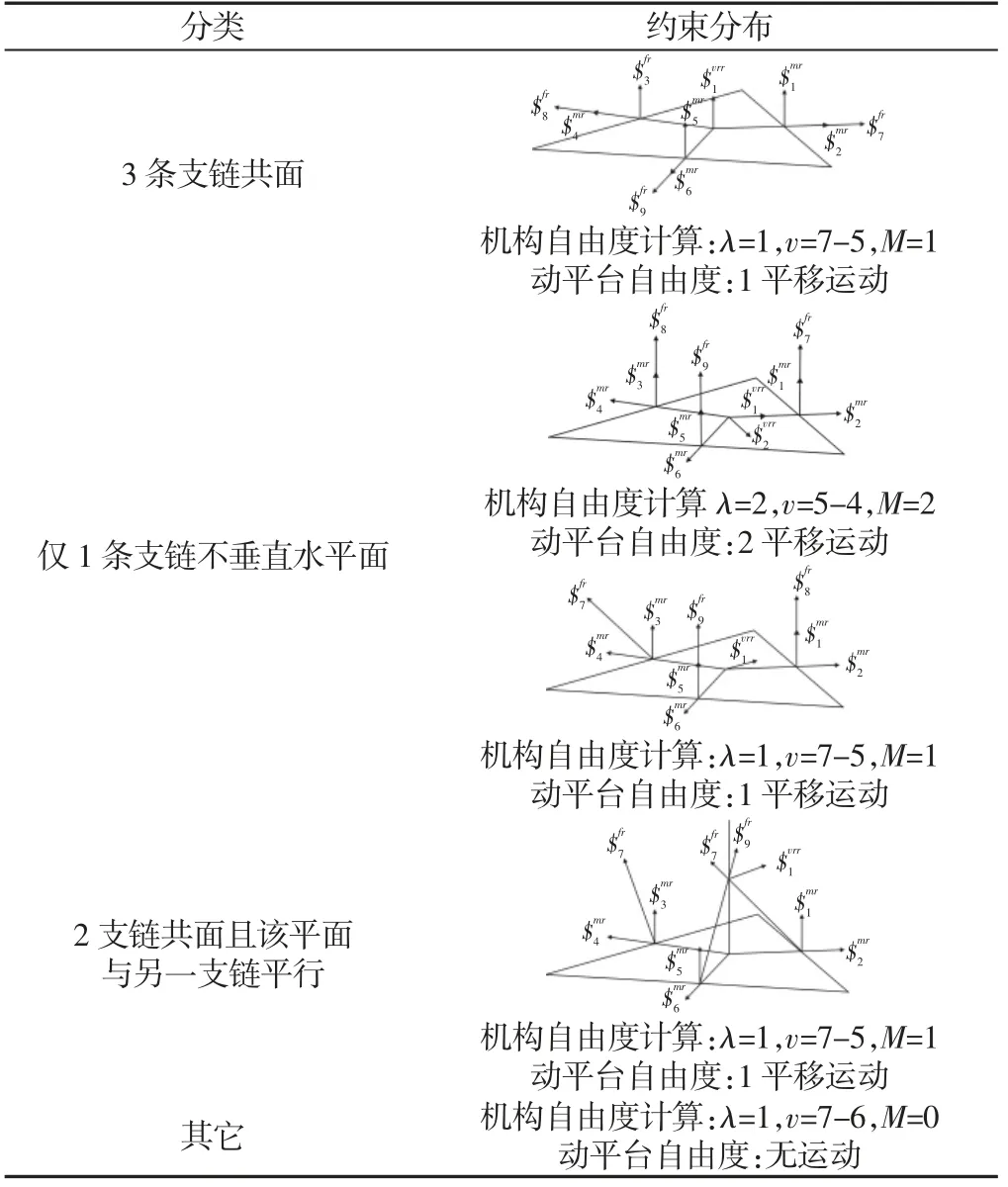
表3 3-RC 在不同位形下的自由度Tab.3 DOF of 3-RC in Different Configurations

當鎖住所有的主動件所獲得的3-RC并聯機構具有表3 中的3 種特征，則此時3-RRC并聯機構處于約束奇異。對比表1 和表3 可以發現存在3 種奇異分別為運動奇異、約束奇異、即為運動奇異又為約束奇異。結合表1 和表3 則得到了合理3-RRC并聯機構機構任一位形下的自由度。

7 結論

（1）利用基于螺旋理論（反螺旋）的自由度分析原理結合動平臺約束分布給出了機構在任一位形下的自由度，當3 個支鏈的3 個運動副軸線都不共面時，機構自由度為3、動平臺有3 個平移運動。

（2）給出了正解、逆解，正解為3 個圓柱面的交點最多有8組解，逆解也可以通過求3 組兩圓的交間接得到最多有8 組解。

（3）給出了工作空間的表達式，發現工作空間為3 個空心圓柱的交可直接用三維制圖軟件繪出工作空間，并發現動平臺位置位于工作空間表面時的所有位形與所有運動奇異位形一致。

（4）在自由度分析的基礎上給出了機構發生運動奇異與約束奇異的幾何條件。

（5）給出的計算分析方法即簡潔又快速，可編制軟件將該機構的自由度、位置正逆解、工作空間、奇異位形計算分析過程程序化，減少大量的重復工作將使得該類機構的設計及優化變得非常簡便。