不確定性雙臂空間機器人自適應模糊優化控制

陳花衛

（銅仁學院大數據學院，貴州 銅仁 554300）

1 引言

自由漂浮雙臂空間機器人（Dual-ArmFreeFloatingSpaceRobot，DFFSR），是由一個本體基座及搭載其上的雙機械臂組成，在太空中忽略微弱重力環境且不受外力控制而處于自由漂浮狀態的機器人系統，因其無需消耗多余燃料、且多機械臂系統具備更好的穩定性，在代替宇航員完成目標抓取、衛星修復、空間站建設等在軌服務任務，較姿態或位置受控、單臂空間機器人系統，具有獨特的優勢，得到了更為廣泛的關注和研究[1-4]。

DFFSR 由于處于失重狀態，其機械臂的運動與基座的運動相互影響，即存在強動力學耦合關系，使得可用于一般機械臂系統的控制方法失效，研究其運動控制問題也因此具有十分重要的意義。文獻[5-7]分別采用傳統非線性反饋控制、變結構滑模控制以及PID 控制方法，實現對DFFSR 關節空間的軌跡跟蹤控制，但均需獲得系統精準慣性參數，然而空間環境往往存在燃料消耗、外界擾動等諸多不確定因素，會對控制精度產生影響。文獻[8]針對不確定性問題，提出了一種基于遺傳算法的補償學習控制方法，實現了機械臂關節空間的軌跡跟蹤控制；文獻[9]基于增廣法提出了一種改進魯棒控制方法，能夠有效解決不確定性DFFSR 的關節運動控制問題；文獻[10]考慮DFFSR 系統關節執行器故障的不確定性因素，設計了一種分散容錯控制器，實現了關節角高精度運動跟蹤控制，但上述文獻均未考慮到系統關節力矩輸出能量優化問題。

針對上述不足，基于系統動量守恒關系及Lagrange 方法，建立DFFSR 系統關節空間的動力學方程；而后，考慮系統慣性參數未知導致慣性矩陣無法求解問題，利用模糊控制理論的萬能逼近特性，通過在線參數辨識建立系統自適應模糊模型；基于此，同時考慮系統存在外界擾動以及輸出力矩的優化問題，利用SDRE 優化控制理論，設計一種自適應模糊優化控制方法，實現了DFFSR系統關節空間的軌跡跟蹤。

2 DFFSR 系統建模

2.1 DFFSR 系統動力學方程

以做平面運動的二連桿DFFSR 系統為研究對象，如圖1 所示。

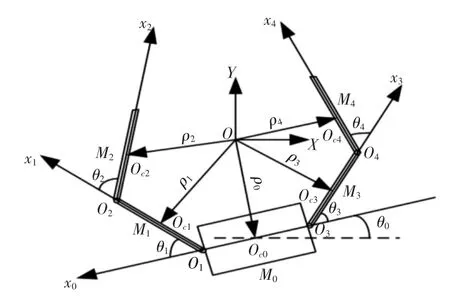
圖1 DFFSR 系統Fig.1 Dual-Arm Free Floating Space Robot Syste m

其由一個基座M0及四個機械臂M1、M2、M3、M4組成，忽略太空環境中的微弱重力梯度，根據動力守恒定理和Lagrange 第二類方程，可推出姿態受控雙臂空間機器人動力學模型、運動學模型以及姿態角與關節角的雅克比關系分別為[11]：

考慮系統自由漂浮狀態下基座位置和姿態均不受控情況，對雙臂空間機器人動力學、運動學模型結構進行分解可得：

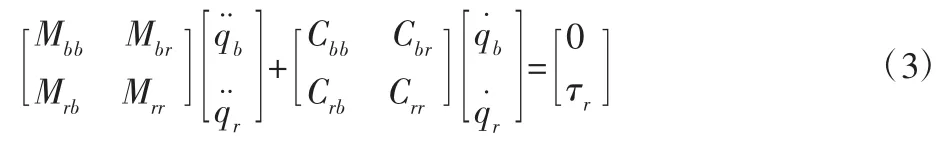
根據式（3），同時考慮存在外界擾動，可進一步推導出DFFSR系統動力學方程為：

2.2 DFFSR 系統模糊建模

定義模糊系統輸出函數形式如下[12]：

3 控制器設計

3.1 SDRE 優化控制理論

考慮仿射非線性系統：

3.2 自適應模糊優化控制器設計

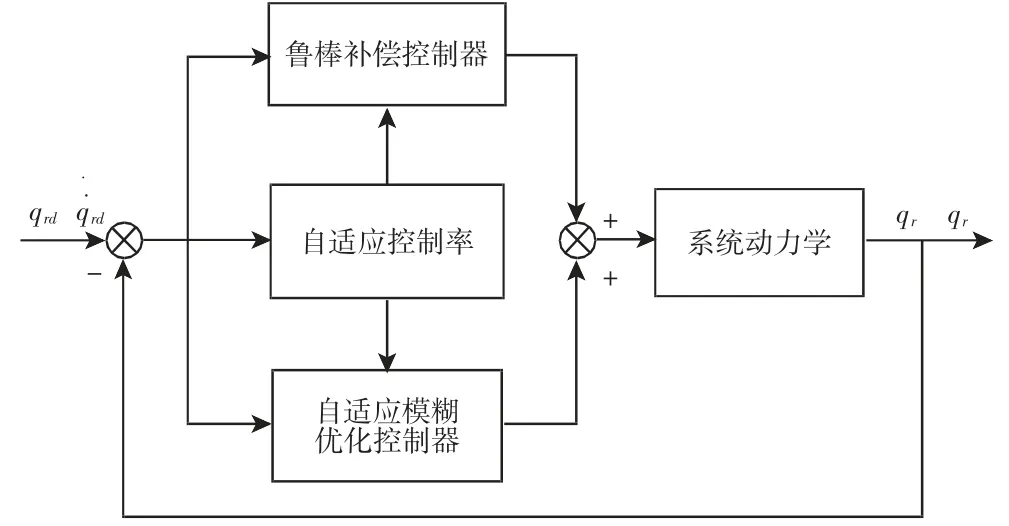
圖2 自適應模糊優化控制系統Fig.2 Adaptive Fuzzy Optimal Control System

DFFSR 系統關節空間控制系統框圖，如圖2 所示。所設計控制器包括優化控制器和魯棒補償控制器兩個部分組成：

4 仿真實例

表1 系統模型參數Tab.1 Model Parameters of System

以圖1 所示的平面二連桿DFFSR 系統為仿真對象，其系統參數，如表1 所示。系統初始運動參數為：

仿真算例一：

考慮系統存在慣性參數未知以及外部擾動等不確定性，使用自適應模糊優化控制律式（17）控制DFFSR 系統關節運動，仿真時間t=15.0s，得到左右兩臂各關節運動軌跡跟蹤情況，如圖3所示。以及各關節輸出力矩，如圖4 所示。

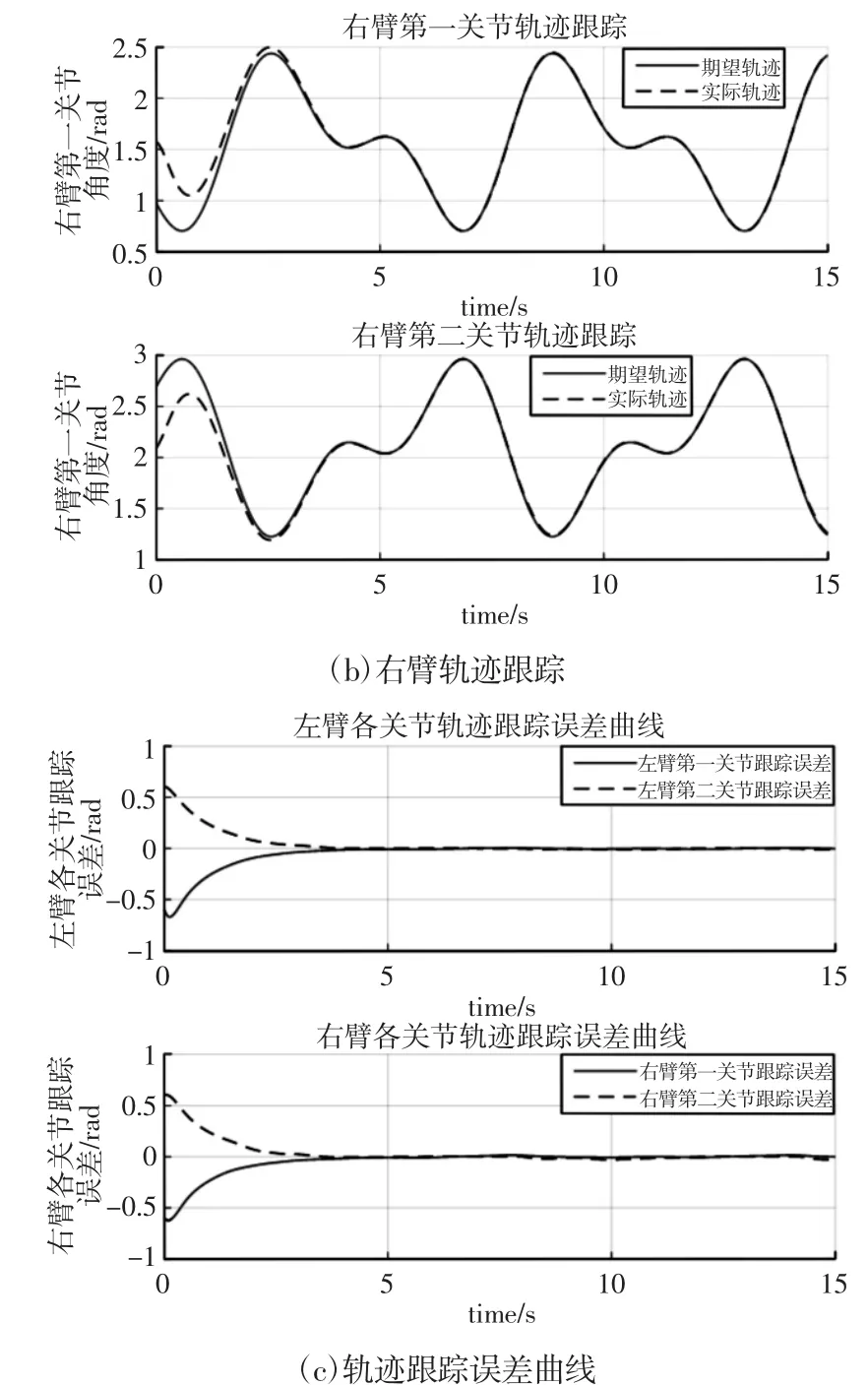
圖3 DFFSR 關節角運動控制Fig.3 Trajectory Tracking of DFFSR in Joint Space

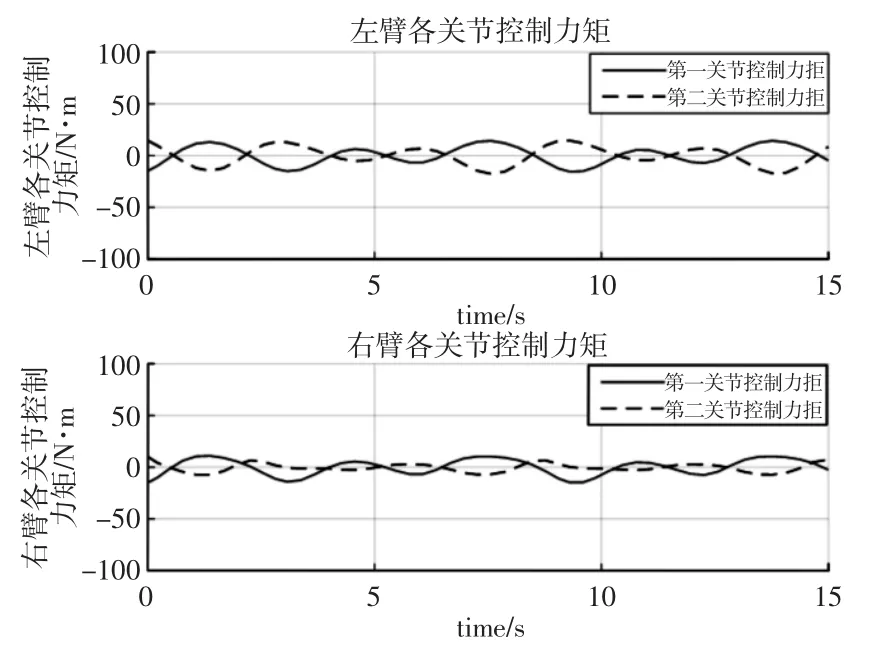
圖4 DFFSR 系統輸出力矩Fig.4 Control Torque of DFFSR System

仿真算例二：

為進一步證明所設計控制器的有效性和優越性，考慮在獲得系統精確參數模型前提下，使用常用PD 控制律式（31）進行仿真實驗，仿真時間t=15.0s，得到左右兩臂各關節運動軌跡跟蹤情況，如圖5 所示。以及各關節輸出力矩，如圖6 所示。

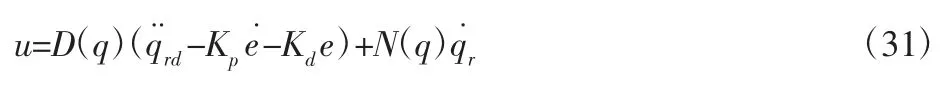
綜合分析以上仿真結果，對比圖3 和圖5，證明了所設計控制器較一般控制器在跟蹤精度以及抗干擾能力上具有明顯優勢；對比圖4 和圖6，可以看出，所設計控制器考慮了力矩優化問題，整體輸出力矩均保持在較小合理范圍內。

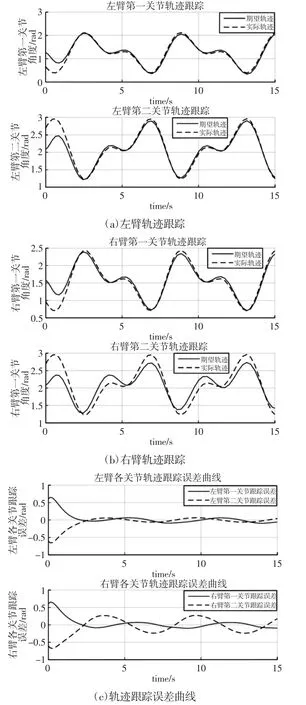
圖5 DFFSR 關節角運動控制Fig.5 Trajectory Tracking of DFFSR in Joint Space

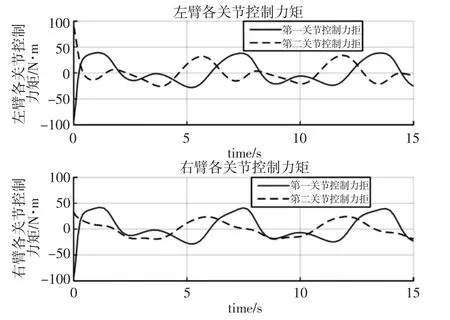
圖6 DFFSR 系統輸出力矩Fig.6 Control Torque of DFFSR System

5 結論

考慮空間環境存在慣性參數未知及外部擾動等不確定性因素，針對DFFSR 系統關節角運動控制問題，提出了一種自適應模糊優化控制方法，一組對比仿真驗證了所提控制方法的主要優點有：（1）無需精確知道系統慣性參數等先驗信息；（2）系統具有較好的抗干擾特性；（3）實現了輸出力矩的優化。