具有微織構形貌的結合面法向接觸剛度分形模型的研究

朱春霞，方 超，劉曦宏，胡成柱

（沈陽建筑大學機械工程學院，遼寧 沈陽 110168）

1 引言

在機械系統中，由于零件的存在，使得零件與零件之間產生大量的機械結合面。這些結合面的接觸屬性在整個機械系統的屬性中占很大一部分，接觸剛度就是其中一個非常重要的特征參數，研究表明，在機械系統總剛度中，機械結合面的接觸剛度約占（60～80）%。由此可見，對于整個機械系統的性能來說，機床結合面的接觸剛度具有非常重要的影響。經過相關學者的大量研究，提出了一系列經典的接觸模型，比如GW 模型和WA 模型等，就表面形貌如何對結合面間的接觸剛度產生影響進行了解釋和預測。為了使模型更加準確可靠，一些學者在GW 模型以及WA 模型的基礎上，更加深入的研究了結合面接觸的問題。如文獻[1]推導出微凸體變形的臨界變形量，在微凸體受載荷作用下變形時，其接觸載荷會連續平滑的變化，基于此提出了的一種新的粗糙結合面接觸模型（簡稱ZMC 模型）；文獻[2]在分形理論的基礎上，提出了結合面間的接觸剛度分形模型（JZZ 模型）。并驗證了所建模型的有效性；文獻[3]基于ZMC 模型，利用分形幾何理論，考慮微凸體在接觸載荷作用下的變形的連續性，建立了微凸體在各種變形狀態下的接觸剛度模型（YANG 模型）；文獻[4-5]基于分形幾何與接觸力學方法建立了法向接觸剛度的分形計算模型。各個學者在結合分形幾何以及接觸力學等相關理論的基礎上，研究粗糙表面上單個微凸體的變形過程，分析了微凸體在各種變形狀態下的接觸剛度，從而建立整個粗糙平面的接觸理論分形模型，但這些研究都是以粗糙平面為研究對象的。

近年來，表面織構技術憑借其良好的界面可控性及摩擦學性能受到了越來越多學者的關注。研究表明，表面微織構會對機械結合面的物理屬性產生影響。經過文獻[6]的研究，發現具有微織構形貌的粗糙表面的磨擦磨損性能得到明顯改善。文獻[7]發現凹坑型織構的凹坑形狀會影響表面的摩擦學性能。文獻[8]研究了不同滑動速度和壓力條件的具有微坑陣列的粗糙表面，在干摩擦的狀態時，由于表面微坑的存，會使試件表面的摩擦因數減小，并且隨著滑動距離的增加，其摩擦因數增加的速度減緩。經過學者們的研究，發現通過在平面上加工微織構可以很好的提高表面的物理屬性。但是這些研究都只研究的表面織構對于摩擦磨損的影響，而微織構對于接觸參數的影響卻并未被系統的研究過。

鑒于此，在粗糙平面接觸分形模型的基礎上，考慮微織構結合面上的表面形貌參數，根據彈塑性過渡變形機制，建立織構平面法向接觸剛度分形模型，考慮微織構界結合面上的表面形貌參數對結合面法向接觸剛度的影響，為微織構結合面的接觸研究提供理論依據，并通過數字仿真計算，研究微織構平面參數對法向接觸剛度的影響。

2 具有微織構形貌的結合面法向接觸剛度理論建模

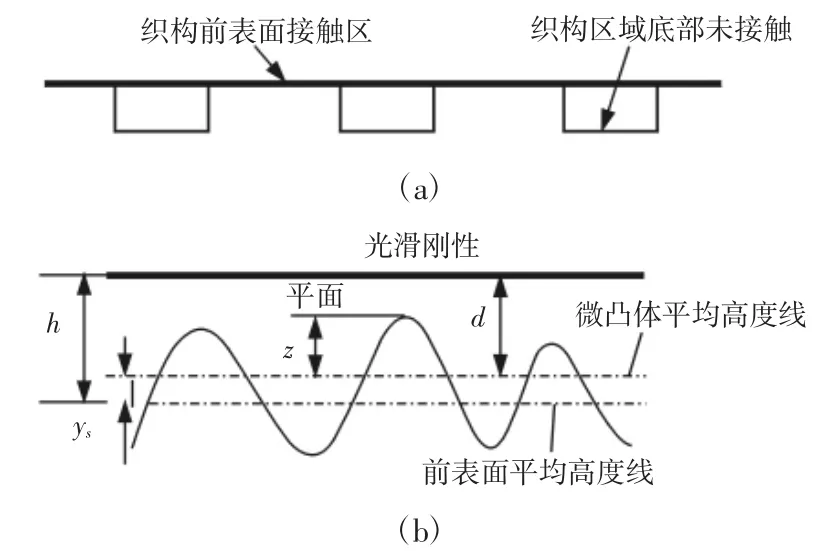
圖1 粗糙織構平面與光滑剛性平面接觸Fig.1 Contact Between Rough Texture Plane and Smooth Rigid Plane

所建模型將具有微織構形貌的結合面簡化為一個具有織構形貌的等效粗糙平面和一個光滑剛性平面的相接觸。結合面由于織構的存在，使得面與面相接觸的時候，有一部分區域未接觸，這部分區域稱為織構區域，此部分區域由于未接觸，其微觀形貌對結合面法向接觸剛度的影響忽略不計，如圖1（a）所示。而對于織構前表面的接觸區域，其接觸模型，如圖1（b）所示。可以看成是光滑剛性平面與粗糙平面相接觸。圖中：h—兩表面之間的距離；z—織構前表面上的單個微凸體的高度；d—光滑剛性平面與前表面微凸體高度平均線之間的距離；ys—織構前表面微凸體的平均高度。

2.1 單個微凸體接觸剛度

在微觀狀態下，織構前表面呈現出凸凹不平的形貌特征，根據分形理論，將織構前表面上的單個微凸體近似等效為曲率半徑為R的球體，其等效曲率半徑R和高度方差σs可由下式計算：

圖2 單個微凸體與剛性平面的接觸情況Fig.2 Contact Between a Single Nicroconvex Body and a Rigid Plane

其中，微凸體法向變行量ω=z-d。由材料力學相關理論可知，在接觸載荷很小的時候，微凸體變形量ω 較小，這時微凸體處于完全彈性變形狀態；隨著接觸載荷的增大，微凸體的變形量ω 也逐漸變大，當微凸體變形量增大到其臨界變形量時，微凸體在接觸載荷作用下的變形開始部分轉變為塑性變形，這時微凸體處于彈塑性變形狀態，臨界變形量的值由微織構表面的材料屬性決定：

分別為兩接觸表面所用材料的彈性模量，ν1、ν2分別為兩種材料的泊松比。

隨著接觸載荷的不斷增加，微凸體的變形量ω 繼續變大，當變形量ω 由ωe增大到ωp時，微凸體進入到完全塑性變形階段，研究表明[12]，ωp=100ωe。

微凸體在三個變形階段的接觸：

（1）完全彈性階段，其變形量ω＜ωe，在這個階段微凸體受到的接觸載荷為w，其表達式為：

織構前表面上的微凸起在接觸載荷的作用下產生變形，前后經歷了三種不同的變形狀態。每個微凸體由于高度不同，所以在相同的表面距離d下，每個微凸體的變形狀態也不一樣，在同一時刻，結合面上同時具有三種變形狀態的微凸體。而對于織構區域未接觸的微凸體，由于未產生變形，可以忽略不計。結合面上所有產生變形的微凸體的接觸載荷wp和法向接觸剛度kp的集合就是整個結合面的接觸載荷Wn與法向接觸剛度Kn。

2.2 具有微織構形貌的粗糙結合面法向接觸剛度的研究

假設在名義接觸面積A內，微織構結合面上的微凸體的數量為N，結合面由于具有微織構形貌，使得處于織構區域的微凸體一直處于未接觸狀態。大量研究表明，機械加工表面的微凸體高度服從高斯分布。因此，對于給定的某一表面距離d，在名義接觸面積內，收到載荷作用而產生變形的微凸體的數量的期望值為：

3 具有微織構形貌的結合面法向接觸剛度分形模型的數值仿真

由上述理論可以看出，當接觸載荷增加時，兩表面之間的距離變小，微凸體前后經歷三種變形狀態。在G-W模型中，為了衡量微凸體在給定接觸狀態下是彈性接觸還是塑性接觸，提出了塑性指數的概念。該參數將材料自身的物理性質與接觸表面的微觀形貌特征相結合。其值反應了粗糙表面上的微凸體從彈性變形狀態轉變為塑性變形狀態的難易程度，值的大小由粗糙表面的物理屬性和微觀形貌特征決定。通過典型的工程表面試驗，可以測得參數β 和σ/R的值，其大小決定了粗糙表面的微觀形貌特征。塑性指數的計算表達式如下：

以45 鋼材料表面的接觸為仿真對象，材料的屬性參數為：E1=E2=207GPa，H=1.96GPa，泊松比v1=v2=0.29。其塑性指數ψ 與β、σ/R參數之間的對應關系，如表1[3]所示。

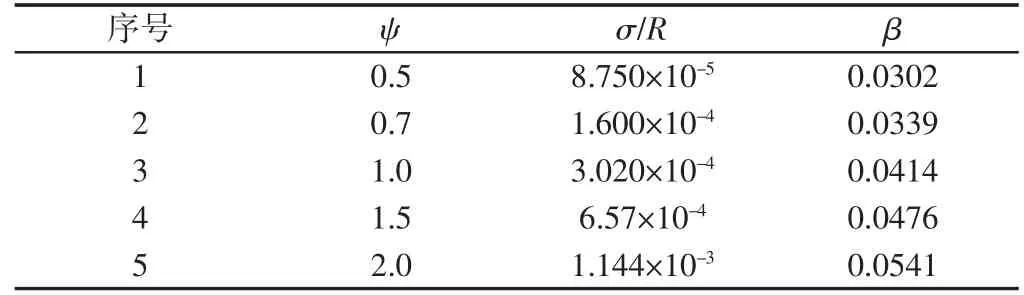
表1 表面工程參數與塑性指數Tab.1 Surface Engineering Parameters and Plastic Index

根據式（16）和式（17），結合表1 中的數據，利用仿真分析研究塑性指數和織構密度對于無量綱法向接觸載荷與無量綱法向接觸剛度之間關系的影響。

當塑性指數與織構密度分別取不同的值的時候，無量綱法向接觸載荷與無量綱法向接觸剛度之間關系，如圖3、圖4所示。從兩張圖中曲線可以看出，當微織構結合面之間的接觸載荷不斷增加時，在不同的塑性指數與織構密度下，結合面的無量綱法向接觸剛度都呈現單調上升趨勢。這是因為隨著接觸載荷的增大，結合面之間的距離變小，產生變形的微凸體的數量也越來越多，并且進入塑性變形狀態的微凸體的數量也越來越多，從而增大結合面的接觸剛度。

當取織構密度為ζ=10%，塑性指數取不同的值時，如圖3 所示。塑性指數的變大，使得微織構結合面之間的接觸剛度增加，并且法向載荷越大，法向接觸剛度的差距越明顯。這是因為塑性指數越小，在相同的接觸載荷下，織構前表面上處于彈性變形狀態的微凸體的數量就越多。由圖中曲線能夠看出，在較小的塑性指數下，兩者的關系曲線近似呈現出線性關系，當塑性指數增大到一定程度的時候，曲線呈現出一定的非線性關系，并且越來越強烈，這是因為越大的塑性指數，會使得在相同的接觸載荷下，進入塑性變形狀態的微凸體的數量大大增加。

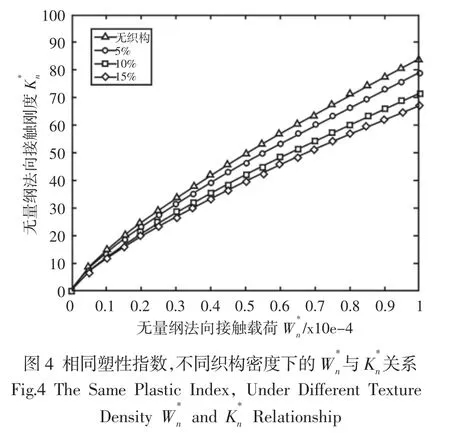
同樣設定塑性指數ψ=1.5，織構密度取不同的值時，如圖4所示。織構密度的增加會使得微織構結合面的接觸剛度變小，這是因為結合面上織構形貌的存在，使得兩個面相接觸時發生形變的微凸體數量減少，從而減小結合面的接觸剛度。并且隨著織構密度的增大，法向接觸剛度增加的速度減慢。所以結合面上織構形貌的存在，會減小結合面上的接觸剛度，并且隨著接觸載荷的增大，織構形貌的這種影響會越來越明顯。

4 結論

在粗糙平面接觸分形理論和接觸分形模型的基礎上，建立微織構平面法向接觸剛度分形計算模型。研究在具有微織構形貌的結合面上由于微凸體變形而產生的法向接觸剛度與接觸載荷的關系。根據微織構結合面的微觀形貌特征，將微織構表面分為織構前表面和織構區域兩部分。用塑性指數表示織構前表面的特征，將材料自身的物理屬性與織構前表面的微觀形貌特征結合；用織構密度表示織構區域參數，將織構區域底部為產生接觸變性的微凸體忽略不計。分析結果表明：塑性指數和織構密度都會對微織構結合面的法向接觸剛度產生影響。在不同的塑性指數與織構密度下，兩表面之間載荷的增加，會減小兩表面之間的距離，使得轉變為塑性變形狀態的微凸體的數量更多，從而使微織構結合面的接觸剛度變大，但會因為塑性指數和織構密度的不同，形成不同程度的上升趨勢。塑性指數的增大，會使得在相同的接觸載荷下，織構前表面上處于塑性變形階段的微凸體的數量變多，從而增加微織構結合面的接觸剛度，并且當塑性指數增加到一定程度時，兩表面之間接觸載荷和法向接觸剛度關系曲線的曲率變大，從而表面出強烈的非線性關系。而微織構結合面織構密度的增大，會使結合面上更多的微凸體在面與面相接觸時，未產生變形，從而減小結合面的剛度，微凸體由于載荷的增大向塑性變形狀態轉化時，這種效果會變得更加明顯。