基于ASRCKF 算法的鋰電池SOC 估算

朱 浩，段 洋

（湖南大學機械與運載工程學院，湖南 長沙 410082）

1 引言

鋰離子電池因為其能量密度高、安全性好、自放電率低和循環壽命長等優點被廣泛用于電動汽車和混合動力汽車。電池荷電狀態（SOC）指電池內部存儲的剩余能量，準確的估算SOC 可以防止過充電或者過放電的發生，同時可以延長電池的使用壽命。但是由于SOC無法直接測量獲得，并且SOC 與放電倍率、環境溫度和循環次數等因素有關，所以要獲得準確的SOC 值是非常困難的。為了準確估計SOC 的值，國內外研究人員提出了很多計算方法，例如，安時積分法[1]、開路電壓法[2-4]、人工神經網絡法和卡爾曼濾波算法[5-8]。卡爾曼濾波算法因其具有閉環和實時的優點成為了鋰電池SOC 估算的研究熱點，其衍生算法：擴展卡爾曼濾波、無跡卡爾曼濾波、容積卡爾曼濾波近年來被廣泛應用于SOC 估算。針對平方根容積卡爾曼濾波估算SOC 時需要準確獲得系統狀態及測量噪聲協方差這一缺陷，將基于電池模型輸出電壓殘差序列的協方差匹配思想引入平方根容積卡爾曼濾波，提出自適應平方根容積卡爾曼濾波算法（ASRCKF）。

2 電池模型參數辨識

卡爾曼濾波算法建立在目標系統的狀態空間方程之上，并且算法的濾波效果好壞很大程度上取決于系統模型的精度。因此，對用于SOC 估算的電池模型有兩點要求。首先要能較為完整的反應鋰離子電池的動態特性。其次，要能從模型較為容易的推導出空間狀態方程。在滿足這兩點要求的情況下最為廣泛使用的是戴維南等效電路模型[9]，如圖1 所示。

圖1 戴維南等效電路模型Fig.1 Thevenin Equivalent Circuit Model

在對戴維南等效電路模型的參數進行辨識之前，需要推導出本文采用的如圖1 所示的戴維南等效電路模型的數學形式，根據基爾霍夫定律，從圖1 所示的電池模型中可以得到式（1）～式（2）。

3 自適應平方根容積卡爾曼濾波

通常非線性離散系統的狀態方程和測量方程可表示為：

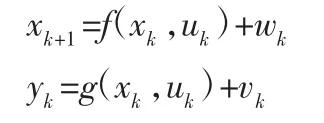
式中：xk—k時刻系統的狀態量；uk—k時刻系統的輸入量；yk—k時刻系統輸出量；f（xk，uk）—非線性狀態傳遞函數；g（xk，uk—非線性測量函數；wk—隨機過程噪聲；νk—影響系統輸出測量值的傳感器噪聲[10]。基于自適應平方根容積卡爾曼濾波估算鋰電池SOC 的步驟如下：

（1）初始化狀態量x^0=［SOC；Up］，誤差協方差P0，過程噪聲和測量噪聲Q，R。

（2）計算容積點

在傳統的SRCKF 算法中，系統噪聲和測量噪聲都被認為是恒定的。然而，系統噪聲和測量噪聲與傳感器的測量精度息息相關，由于傳感器漂移引起的隨機干擾以及由鋰離子電池的時變特性引起的參數不確定導致實際電池系統使用環境中系統噪聲以及測量噪聲是不斷變化的。通常，系統和測量噪聲的初值通過經驗獲取，并且需要花費一定時間去調節參數以獲得最優的濾波效果。另一方面，固定的噪聲值會導致算法對系統狀態量的估算出現偏差，甚至失效。因此，為了在算法迭代過程中實時獲得準確的系統及測量噪聲協方差，提高算法的性能，將基于電池模型輸出電壓殘差序列的協方差匹配思想引入SRCKF，提出基于殘差序列的自適應平方根容積卡爾曼濾波算法，噪聲自適應方程見下式[11]。

4 實驗及結果分析

選擇18650 型鋰離子電池作為實驗對象，該電池額定容量為2.2Ah，額定電壓為3.7V，采用單體充放電機對電池進行充放電測試，并對電池電壓進行實時檢測，母線電流及電量則通過單體充放電機內部的高精度電流傳感器檢測和計算，所有數據都會被記錄在上位機中，實驗環境，如圖2 所示。為了驗證算法在實際道路工況下的精度，對電池進行了UDDS 工況測試。UDDS 工況包含車輛在城市道路環境下可能遇到的各種情況，比如怠速、勻速、加速和減速。因此，UDDS 工況已成為整車性能測試的非常重要工況之一。由于實驗條件限制，首先通過advisor2002 對UDDS工況進行軟件模擬，然后將模擬得到的電流數據根據電池容量等比例縮小即可得到本實驗充放電電流數據，如圖3 所示。相應的電池電壓變化數據，如圖4 所示。電池數據的采樣頻率為1Hz，放電為負，充電為正。設置算法初值x^0=［1；0］；P0=［0.1，0；0，0.1］；Q=［5e-5，0；0，5e-5］；R=1，在Matlab2014b 環境下對算法進行仿真，結果，如圖5 所示。從圖5 中可以看出，SRCKF 算法和ASRCKF算法都可以很好的估算鋰電池SOC，不過ASRCKF 算法的估算曲線更接近真實SOC 曲線。SOC 誤差的對比圖，如圖6 所示。從圖6 可以更明顯的看出ASRCKF 算法的優越性，在仿真初期，由于系統狀態及測量噪聲的初始值不準確，導致SRCKF 算法產生的誤差突增，然后在算法的修正下緩慢下降，在仿真中期達到理想值；而ASRCKF 算法在每次迭代過程中都會自適應更新狀態和測量噪聲，因此，不準確的噪聲初值對算法的估算效果影響不大，在仿真初期誤差即達到了理想值。這兩種算法的誤差分析結果，ASRCKF 算法較傳統SRCKF 算法精度有明顯提高，傳統SRCKF 算法估算SOC 的均方根誤差為3.41%，而這里提出的ASRCKF 算法估算誤差不到1%，僅為0.97%，如表1 所示。更重要的是，ASRCKF 在噪聲初值不準確的情況下表現出的穩定性和適應能力更強。

圖2 電池實驗環境Fig.2 Battery Experiment Environment

圖3 DST 電流樣本數據Fig.3 Current Sample Data Under DST

圖4 DST 電壓樣本數據Fig.4 Voltage Sample Data Under DST

圖5 SOC 算法仿真對比Fig.5 Comparison of SOC Algorithm Simulation

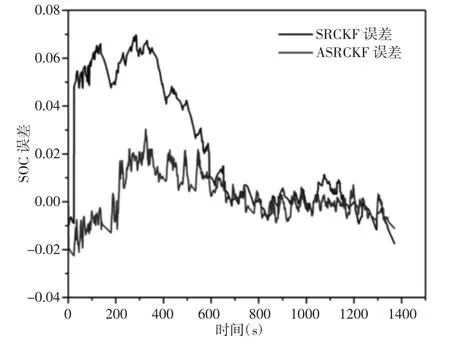
圖6 SOC 估算誤差對比Fig.6 Comparison of SOC Estimation Error

表1 SOC 估算誤差對比Tab.1 1Comparison of SOC Estimation Error

5 結論

（1）當系統狀態及測量噪聲初值不準確時，傳統SRCKF 算法在UDDS 工況下估算SOC 的均方根誤差為3.41%，最大誤差達到了6.97%；而這里提出的ASRCKF 算法產生的均方根誤差僅為0.97%，最大誤差為3.08%。（2）為了將不準確噪聲初值帶來的SOC 估算誤差修正至1%以內，傳統SRCKF 算法需要接近600 個步長，而ASRCKF 算法僅需要100 個步長。（3）通過對算法在精度以及收斂速度方面的定量分析，這里提出的自適應平方根容積卡爾曼濾波算法對不準確的噪聲初值具有更好的適應能力，同時具有更高的估算精度，考慮到電動汽車復雜的運行環境，ASRCKF 算法具有很好的應用前景。