軍用工程機械急造軍路機群優化配置研究

杜毛強，何曉暉，王 強，朱曉基，魏文海

（1.陸軍工程大學野戰工程學院，南京 210007；2.解放軍32228 部隊23 分隊，福建 廈門 361100）

0 引言

急造軍路是軍用工程機械遂行機動工程保障任務之一。根據急造軍路的任務性質，通常可將其分為清除塌方、填塞彈坑和壕溝、修復崩塌路基等3種具體任務，且往往需要在不同地域同時開展。每個任務均涉及到推土機、挖掘機、裝載機等多種類型軍用工程機械協同作業。因此，軍用工程機械遂行急造軍路任務是一個多型裝備、多種任務、多點同時展開的機群作業問題。研究機群的優化配置既有重要的現實意義，又有重要的理論研究價值，是該領域的研究熱點。Manuel Parente［1］等人整合了啟發式算法和數據挖掘技術的優點，以搜索工程機械的最佳配置；馮柯［2］等人以充分發揮現有工程機械作業效能為目標，運用線性規劃的方法建立了工程機械機群優化配置的數學模型；曹豪榮［3］等人采用隨機過程排隊論方法得到基于快速施工的最優機械配置方案；Faridaddin Vahdatikhaki［4］等人提出了一種多智能體系統，有效改善施工機群的協調問題；鄭雨茜［5］等人運用極差最大化組合賦權法改進了現有的機群配置模型。但上述研究僅限于單任務、單點展開作業的情況，對多型裝備、多任務、多點同時展開作業的機群配置問題考慮較少。本文針對軍用工程機械遂行急造軍路的機群配置的現實需求，以完成任務時間最短為優化目標，基于整數線性規劃理論建立了機群優化配置模型，為軍用工程機械機群優化配置提供了決策支持。

1 優化配置模型構建

軍用工程機械機群的配置需要根據任務類型、工程量以及機械的作業能力確定，因此，必須對機群配置問題進行建模分析，以制定最優的機群配置方案。

1.1 任務描述

急造軍路可分為3 種具體任務：清除塌方、填塞彈坑和壕溝、修復崩塌路基。在遂行任務時，3 種任務往往同時開展，且都需要推土機、挖掘機、裝載機協同完成。將軍用工程機械機群中的每一臺工程機械看作一個單位，單位集：

其中，T 表示推土機，W 表示挖掘機，Z 表示裝載機。各種機械數量分別表示為：推土機n1，挖掘機n2，裝載機n3。

假設共有推土機a 臺，挖掘機b 臺，裝載機c臺，任務數量為e。機群配置的任務—單位分配關系表示為：

挖掘機：

裝載機：

1.2 問題建模

考慮每個任務如何配置機群，能夠使總任務完成的時間最少。由于總任務完成的時間等于各任務完成時間tj的最大值。軍用工程機械機群優化配置模型的目標函數為：

需要滿足的約束條件有：

1）機械數量約束。

各任務機械數量不得超過該類機械現有數量：

2）任務完成時間約束。

各任務必須在要求時間限制內完成：

其中，Ci為任務i 的工程量，Qj為單位j 的作業率。

3）各任務要盡可能地同時完工，避免出現某段任務完工過早或過晚的現象，以保證機群資源更加均衡合理分配使用。

4）每個任務必須都有3 種不同類型的機械，且數量為整數。

通過對問題的描述和約束條件分析，可建立如下數學模型：

2 模型求解

機群的配置模型求解是一個離散組合優化問題，而啟發式搜索算法是解決此類問題的有效方法。結合本研究問題的特殊性，在對離散粒子群算法［6］、隱枚舉法［7］、遺傳算法［8］等方法進行比較的基礎上，本文選用粒子群算法求解優化配置模型。該算法具有收斂速度快、全局優化性好的特點，其應用領域已從連續空間優化問題擴展到離散組合優化問題［9］，在解決機群優化配置問題上優勢尤為明顯。

2.1 算法流程

離散粒子群優化算法（BPSO）隨機初始化一群粒子，每個粒子代表多為空間中的一個點，它使待優化函數最值的一個潛在解，隨著算法運行，粒子不斷逼近函數的最值。在每次進化過程中，粒子通過跟蹤兩個“極值”來更新自己所在的位置。第1 個極值為粒子自身找到的最優位置，相對應的適應值叫pBest；另一個極值是整個種群當前找到的最優位置，相對于的適應值稱為全局極值gBest。其流程圖如圖1 所示。

圖1 算法流程圖

2.2 粒子編碼的設計

對于機群優化配置問題，每個粒子位置對應一個配置方案，這樣就將每一種配置方案映射成一個粒子，粒子的飛行表示從一個配置方案到另一個配置方案的選擇。隨著算法的收斂，粒子逐漸逼近最優配置方案。遂行急造軍路任務的機群配置矩陣為：

式中，Tij，Wij，Zij∈｛0，1｝。可進一步將其分解為子矩陣：分別表示推土機、挖掘機、裝載機在各任務的配置情況。

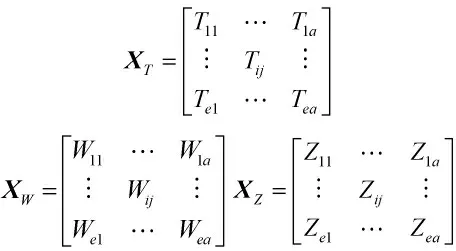
設種群中粒子位置的集合為：

式中，PO P 為種群大小。

種群中粒子位置如圖2 所示。

圖2 粒子種群位置

例如，任務1、任務2、任務3 分配推土機、挖掘機、裝載機各1 臺的矩陣粒子編碼可表示為

這樣的編碼方式可以直觀地將各任務的機群配置情況表示出來。

2.3 粒子速度與位置更新方式

由于每個單位只能被分到一個任務，每個任務至少分配一個單位，所以位置矩陣每列的和恒等于1，每行的和大于等于1。傳統的BPSO 在處理粒子位置的更新時，粒子中1 的個數可能發生改變，出現一列都為0 或一行都為0 的情況，故需對BPSO 進行改進。文獻［10］提出了一種速度位置更新公式：

按照本文的編碼方式，機群的配置方案由粒子位置矩陣各行1 的數量決定，所以各行0、1 的順序沒有實際意義。例如以下兩個矩陣：

均表示在任務1、任務2、任務3 分配推土機、挖掘機、裝載機各1 臺。所以在粒子位置矩陣按照式（9）迭代時，可對算法進一步改進。若子矩陣各行的和沒有改變，則不計算適應值，返回重新迭代，這樣可以加快收斂速度。改進的BPSO 速度與位置更新方式如圖3 所示。

3 案例分析

本文以文獻［2］中的構筑急造軍路任務為例。該急造軍路共有3 條道路的構筑任務，各道路的偵查情況為：道路1 大面積塌方，道路2 有連續彈坑，道路3 路基崩塌，據此將任務區分為：任務1 清除塌方，任務2 克服連續彈坑，任務3 修復崩塌路基，各任務工程量如表1 所示。現有推土機10 臺，挖掘機7 臺，裝載機6 臺，各類機械在理想條件下（即機械技術狀況良好、中等土壤、白天、無雨雪等），對各任務的作業率如表2 所示。文獻［2］利用線性規劃方法得到的優化配置方案完成總任務時間為4.02 h。

表1 各任務工程量（m 3）

表2 各任務工程機械作業率（m 3/h）

根據本文建立的數學模型，以最小化總任務完成時間為優化目標，用改進的BPSO 求解，并利用Matlab R2015b 進行編程計算。模型求解的優化過程如下頁圖4 所示。

可見，目標函數適應值在算法迭代40 次左右達到收斂，總任務完成時間最小值為3.931 9 h，優于文獻［2］利用線性規劃方法求得的任務完成時間4.02 h。算法在仿真20 次以后趨于穩定，說明算法在解決機群優化配置問題上具有快速的尋優能力。最優結果的機群配置矩陣為：

圖3 粒子速度與位置更新方式示意圖

圖4 模型求解優化過程

得到軍用工程機械機群的最優配置方案如表3所示。

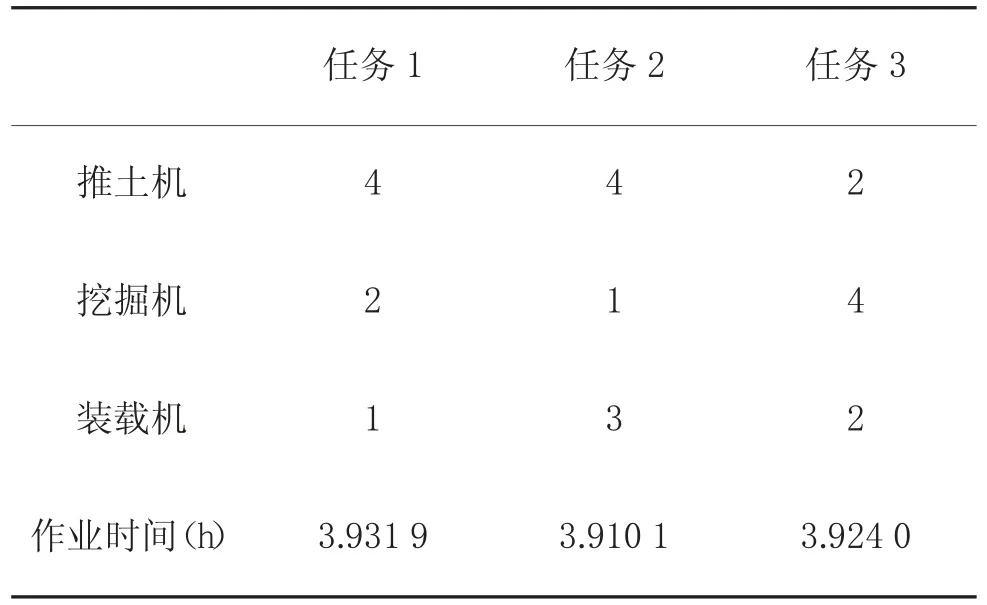
表3 最優機群配置方案

4 結論

本文對軍用工程機械遂行構筑急造軍路任務面臨的多型裝備、多種任務、多點同時作業的機群優化配置問題進行分析，提出了基于整數線性規劃理論建立機群優化配置模型，并運用改進的離散粒子群算法求解模型的機群優化配置方法。通過案例分析表明，該方法能有效解決機群的優化配置問題，提高軍用工程機械的保障能力。