三維水翼梢渦氣核運動特性的數值模擬

郭春雨， 薛嶸， 胡健， 王戀舟

(1.哈爾濱工程大學 船舶工程學院，黑龍江 哈爾濱 150001； 2.西南交通大學 力學與工程學院，四川 成都 611756)

梢渦在有限展長的翼型繞流現象中普遍存在。當流動流過有攻角的有限長水翼的端部，水翼上下表面的壓力差會驅使流動從下表面的高壓側流向上表面的低壓側，從而形成三維的旋渦，我們把它稱為梢渦[1]。梢渦具有強烈的旋轉效應，使得渦核中心的壓力值顯著降低。在水動力學領域，梢渦引起的壓降會驅使水中的氣核卷入渦核內部，產生空化。梢渦空化會降低水翼結構的水動力性能，并會伴隨出現強烈的噪聲。為了避免梢渦空化帶來的危害，需要對它的形成機理進行分析。

學者們進行了大量的試驗來研究梢渦的細微結構。Giuni等[2-3]通過煙跡試驗，得出梢渦是由起始于壓力面的主渦和2個分別起始于吸力面和壓力面的次級渦演化形成的。徐良浩等[4]使用2D-PIV和3D-PIV對梢渦的二維和三維速度場進行了測量，獲得了不同工況下的渦核位置、尺寸及速度分布，得出了渦核在三維空間內的擺動特性。Maine等[5]通過對3種不同翼型剖面的實驗觀測，研究了水翼的縱傾和側斜對梢渦形成的影響。梢渦試驗往往伴隨著空化初生現象。Arndt等[6]通過LDV試驗指出，梢渦空化發生的必要條件是分布在水中的氣核進入渦核中心并發展為足夠大的氣泡。在這個基礎上，Arndt等[7]進一步研究了壓力變化和水中含氣量對梢渦空化的影響。他們得出在含氣量多的水中，梢渦空化多發生于水翼梢部；而在含氣量較少的水中，梢渦空化的起始位置在梢部流動后端。

隨著計算機運算能力的逐步發展，采用各種湍流模型來模擬梢渦逐步成為可能。相比各種試驗手段，數值模擬可以觀察到更加細微的渦結構，從而更好地去觀察梢渦的演化，進而了解梢渦空化初生的規律[8]。盡管如此，由于梢渦尺寸很小，壓力梯度很大，模擬梢渦是一件具有挑戰性的工作[9]。Decaix等[10]采用RANS模型對截面形狀為NACA 0009的水翼梢渦進行了數值模擬，數值結果表明RANS方法可以準確模擬出梢渦的渦核位置、平均速度場等的時均特性。蒲汲君等[11]使用k-w、DES和LES模型分別對水翼的梢渦流場進行了數值模擬，并使用氣泡靜力平衡方程計算了空化初生現象。結果表明LES模型可以很好地模擬梢渦處流場，此外應用氣泡靜力方程可以準確計算初始梢渦空泡數。當涉及空化初生問題時，可以耦合球形空泡模型來模擬氣泡運動[12]。Rayleigh[13]建立了球形氣泡模型，用于描述球形氣泡在變化的壓力場中的半徑變化。許多研究致力于分析氣泡及顆粒在水中的運動，Maxey等[14]給出了一種描述剛性球體的運動方程，可以很好地描述球形空泡的運動規律。Park等[15]利用他的計算方程，計算了氣泡在水翼梢部的運動。

本文以剖面為NACA 0015的三維水翼為研究對象，采用大渦模擬(large eddy simulation, LES)方法來模擬水翼梢渦。將計算結果與試驗值[16]進行對比，滿足精度要求之后，在這個基礎上開展基于離散元 (discrete element method, DEM)模型的氣核在水中運動研究，分析氣核在梢渦作用下的演化規律。整個計算工作在數值模擬軟件STAR-CCM+下完成。

1 幾何模型與數值模型及網格劃分

1.1 幾何模型

幾何模型與文獻[17]中試驗所用翼型保持一致。如圖1所示，翼型截面形狀為NACA 0015，弦長C=0.15 m，展弦比6.6，攻角12°，端部裝有圓形導流罩。計算域布置以及邊界條件如圖2所示。為了節省計算資源，將水翼的展長選為3.3倍弦長，遠離梢部的一端貼近壁面，并將壁面設置為對稱邊界條件，從而節省一半的網格數量。由此，該計算域的寬為4.5C，高為4.5C，水翼前端距速度入口距離為3.3C，后端距壓力出口距離9C，其余壁面均設置為無滑移壁面條件。計算環境為25 ℃的水，此時密度998 kg/m3，動力粘度0.000 889 9 kg/(m·s)，流速10 m/s，從而雷諾數Re=1.5×106。

1.2 湍流模型

本研究采用大渦模擬(large eddy simulation, LES)求解流體域中任何位置的空間湍流結構。網格尺寸超出選用尺寸的大尺度旋渦進行直接求解，小于選用網格尺寸的細微旋渦結構采用亞格子進行模擬。從而在復雜的流動模擬中得到細微旋渦結構的流動圖像。

圖1 水翼模型及導流罩Fig.1 Hydrofoil model with round end cap

圖2 計算域布置條件Fig.2 Compute region conditions

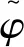
(1)

式中φ表示速度分量、壓力、能量或組分濃度。

將分解的求解變量插入納維-斯托克斯方程可得到已濾波物理量的方程。濾波后的質量和動量的傳輸方程可以寫為：

(2)

(3)

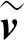
湍流應力張量現在表示為亞網格尺度應力。這些應力產生自較大的已求解渦流與較小的未解析渦流之間的相互作用，使用Boussinesq近似進行建模，為：

(4)

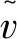
(5)

亞網格尺度湍流粘度μt必須由能夠解釋小渦流對已求解流體的作用的亞網格尺度模型來描述。采用WALE亞網格尺度模型，使用混合長度假設來對亞網格尺度應力建模：

μt=ρΔ2Sw

(6)

式中：Δ為長度尺度或網格濾波器寬度，使用網格單元體積定義如下：

Δ=min(κd,CwV1/3)

(7)

式中：Cw為模型系數，典型值介于0.5(對于均勻各向同性衰變湍流)～0.325(對于通道流)之間;κ為馮卡門常數；Sw的定義見文獻[17]。

1.3 DEM模型

本研究采用DEM模型對氣核的運動特性進行模擬。離散元方法(DEM)是一種基于拉格朗日方法的數值方法，通常用來模擬大量相互作用的離散對象(通常是顆粒)如何運動。根據格雷斯等[18]的研究，氣核直徑通常在30～300 μm，在這一尺度下，氣核在運動過程中可以維持較為穩定的球形外形，從而在本研究中，將氣核簡化為不可形變的球形顆粒，應用DEM方法對氣核進行建模。

DEM方法以牛頓第二定律作為控制方程：

(8)

(9)

式中：mi、vi和ωi分別表示顆粒i的質量、速度和角速度；Ii為顆粒i的轉動慣量，對于球形粒子，Ii=2miRi2/5，Ri為顆粒i的半徑；Fg=mig為顆粒i的重力；,Ffluid為流體對顆粒i的作用力(包括阻力、升力、附加質量力和浮力等)；Fij為顆粒i與顆粒j或墻壁之間的碰撞力以及其他作用在粒子上的非接觸力；Tij為接觸力矩，表示除顆粒重力以外的接觸力在粒子上產生的扭矩。

STAR-CCM+中的DEM模型在拉格朗日架構內實現，并使用拉格朗日相模型對粒子進行定義。本文使用DEM方法對氣核進行模擬，并與CFD結合使用，從而求解由顆粒組成的離散相的氣核在流體介質中的運動。其中，流場的求解由大渦模擬完成；氣核的運動基于拉格朗日方法,由式(8)、(9)進行求解。STAR-CCM+將對DEM粒子和流體之間的相互作用進行建模，并將LES計算得到的流場中各網格處的力代入到式(8)、(9)中，對氣核的運動進行求解。

1.4 網格劃分

采用Star-CCM+對水翼模型進行面網格重構，形成表面三角化良好的高質量面網格，以面網格為基礎生成帶有邊界層和切割體網格的非結構體網格。邊界層共劃分12層棱柱層網格，并將y+值控制在1以下，從而滿足LES模擬的計算要求。對水翼表面和梢渦區域的體網格進行加密處理，最終確認計算域網格總數約為780萬，網格細節如圖3所示。

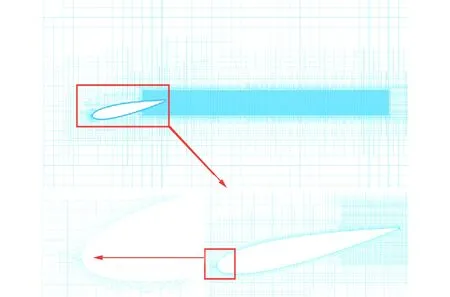
圖3 全局網格、加密區和邊界層Fig.3 Overall mesh condition, refining region and boundary layer mesh

2 計算結果分析

2.1 數值驗證

為驗證所采用的數值模型是否滿足計算要求，以數值模擬結果與文獻[16]中的相關試驗工況的結果進行對比，來驗證模擬結果的準確性。監測水翼表面受到的力在x和y方向上的分解值，即阻力和升力，并將升力換算為力系數并與試驗值進行對比。可以得出本次數值模擬得到的升力系數為1.18，對比文獻[16]中對應的試驗結果的升力系數為1.24，相對誤差在4.8%以內，可以認為本文的計算結果與文獻中的結果較為吻合，從而本文采用的數值模型是可靠的。

圖4為梢渦附近流場無因次垂向速度沿弦長方向分布結果與試驗結果的對比。在水翼隨邊后端0.2倍弦長距離的位置布置一排監測點，用于監測梢渦附近的垂向速度值，如圖5所示。本研究采用的大渦模擬方法是一種瞬態的模擬方法，因此各監測點需要將監測一段時間后的速度值進行平均化，再將平均化后的垂向速度值UZ除以來流速度U∞進行無因次化，由于梢渦軌跡近似于X軸方向，從而認為UZ/U∞的值作為梢渦的無因次切向速度。從圖5中可以看出，數值模擬對渦核位置附近的切向速度值捕捉與試驗值較為相符，除了在峰值和谷值處有一定的偏差。這是因為無量綱化速度的極值位于梢渦渦核位置，由于渦核高強度的旋轉帶來了切向速度的極值。試驗中使用的渦量計布置位置為一系列等間距點，在峰值附近，布置點較少而漏掉了極值；而模擬中在渦核位置附近布置了更多的監測點，從而監測到渦核的極值。通過對數值模擬中速度場的驗證，可以認為本研究對于流場的模擬具有較高的精確度。

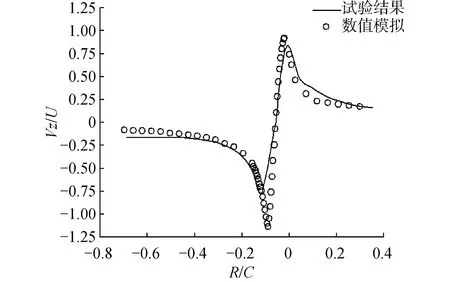
圖4 水翼后端0.2倍弦長處梢渦附近垂向速度對比Fig.4 Comparison of vertical velocity across the tip vortex at r=0.2C

圖5 水翼后端0.2倍弦長處垂向速度監測位置Fig.5 The location of vertical velocity monitoring at r=0.2C

2.2 結果分析

2.2.1 流場結構

本節從梢渦結構方面來分析梢渦流場數值模擬的結果。使用Q判據來可視化渦結構，Q判據的計算公式為：

(10)

式中:Ω為渦張量;S為應變率張量。

圖6為Q=10 000 s-2的瞬時梢渦等值面，并采用渦量幅值進行著色。為了展現整個梢渦位置渦量場的細節，分別從水翼側面和后方視角展示了渦量場的整體與局部。由圖6(a)展現的整體渦結構可知，本文采用的LES模型結合水翼后端位置網格加密，可以捕捉到精細的梢渦結構，且梢渦主渦的強度值在1 600 s-1附近可以保持在5倍弦長之上的距離，這同Bailey等[19]的試驗結果相符。從等值面渦量場可得，本研究對于梢渦區域的網格細化程度滿足分析要求。

圖6(b)展示了近梢部端渦量場的渦結構。從圖中可以看出，梢部渦系由2部分組成，序號為1的渦來源于水翼壓力面梢部的位置邊界層發生分離，進而產生渦強很高的梢渦；序號為2的渦來源于水翼吸力面靠近梢部的位置，這部分的流動在從水翼隨邊分離后，在梢渦的強旋轉效應下形成了包裹在梢渦外邊的渦系。

圖7為不同截面上的渦量云圖，截面的選取參考圖8，選取水翼隨邊為起始位置，每隔0.5倍弦長距離共作6個截面，形成圖7的截面。從渦量云圖可以觀察到，梢渦位置具有多重渦結構組成的渦系。壓力面形成一個主渦和一個二次渦，在向下游遷移到1.5倍弦長附近發生融合；吸力面發生流動分離并形成多個較弱的渦心，在向下游發展的過程中渦量逐漸耗散。

圖6 Q=10 000 s-2等值面的渦量場及細節展示Fig.6 Vortex field and detail display of iso-surface with Q=10 000 s-2

2.2.2 氣核運動特性分析

本節在得到穩定發展的渦量場的基礎上，向流場中加入DEM粒子所表示的氣核，來研究水翼梢部氣核的空間演化過程。

拉格朗日相的DEM粒子需要通過噴射器加入到歐拉相的流場中進行求解。如圖9為DEM粒子的噴射點位置，在水翼的端部，沿弦長方向每隔1/10弦長設置一排噴射點，這些噴射點沿圓形導流罩長度方向間距為1 mm。隨后在拉格朗日相下設置氣核的物理屬性，在本研究中，氣核的半徑為100 μm，密度為氣體密度。如此設置后在流場中噴射點的位置各出現1個氣核，隨后氣核將在DEM方程的控制下，基于受到流場中的各種力隨梢渦向水翼后端遷移。

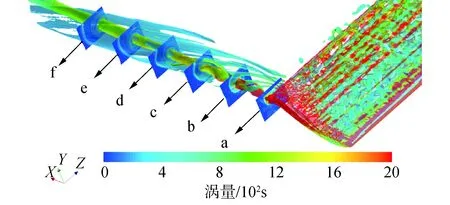
圖7 水翼隨邊后端渦量云圖截面分布Fig.7 The distribution of vorticity contour section behind hydrofoil′s trailing edge

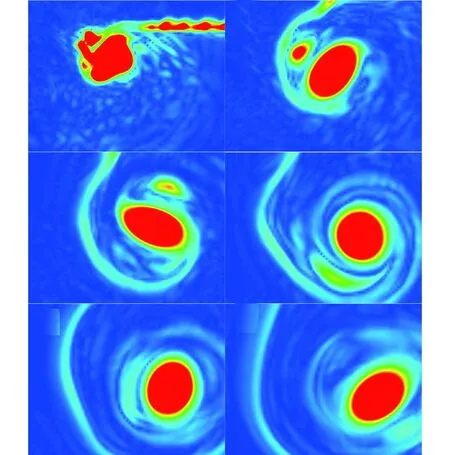
圖8 不同截面上渦量云圖Fig.8 Vorticity contour in typical sections

圖9 DEM粒子噴射點位置Fig.9 DEM injector positions distribution

如圖10所示，選取噴射點位于端部中軸線并距端部垂直距離為1 mm處的氣核流跡進行分析。圖中用速度場對氣核流跡進行著色，深色線條為和氣核初始位置相同的流線。從流線軌跡可知，初始流動位置越靠近水翼前緣，在向下游遷移的過程中會出現遠離梢渦核心的趨勢；而初始位置接近水翼后緣的流動會被梢渦捕獲。對比經過各氣核初始位置的流線，可以對這一現象進行解釋。由于梢渦在水翼壓力面后端開始產生，因此水翼端部后半端的流動受旋渦影響較大，從而這些位置的流線緊緊跟隨梢渦運動；水翼端部前半段產生的流線表明，經過這部分的流動會沿水翼展向遷移，在隨邊與水翼分離后，受到圖6(b)中渦系2的影響，隨著包裹在渦核外部的渦系旋轉運動。氣核具有一定的流線跟隨性，從而伴隨著2種不同的流線運動狀態，氣核也具有2種不同的運動狀態。

圖10 初始位置距端部1 mm處氣核流跡及流線對比Fig.10 Comparison between nuclei track and streamline with initial location from round end=1 mm

氣核的流跡雖然表現出一定的流線跟隨性，但是與流線還是有一些區別。從圖6(b)細節可以看出，氣核的遷移軌跡極易受到渦強的影響。在水翼壓力面梢渦的主渦剛形成的位置產生的氣核，會迅速遷移到旋渦中心，跟隨渦核向下流旋轉運動；在水翼前端部產生的氣核，在隨流線遷移到與水翼分離后，遷移軌跡位于梢渦外部包裹的渦系內。可以得出，氣核先隨流線向后遷移，當軌跡附近出現強渦量區域后，氣核會向渦強較強的位置進行遷移，從而不再跟隨流線。

接下來選取部分氣核，對它們流跡的特征進行分析。如圖11分別為1、2、5、7、9號的噴射器發射的氣核流跡，在向下游發展的過程中垂向速度的變化曲線。對遷移距離除以弦長得到L/C，垂向速度除以來流速度得到V/U進行無量綱化處理。由于水平長度7C以后的網格位于梢渦加密區外，因此不再取之后的速度進行分析。從曲線中可以看出，為1號和2號的氣核由于流跡位于旋渦核心外部，在遷移的過程中速度振蕩頻率較小。而其余氣核流跡位于渦核內部，可以按照振蕩特性將軌跡分為3個階段。如圖11(c)所示，第1階段是從氣核剛進入流場到遷移到水翼尾端位置，這一階段氣核開始進入剛形成的梢渦內部，垂向速度的變化表現出較大的隨機性。這是由于這一階段旋渦剛開始形成，而氣核不再跟隨流線運動并開始進入渦核內部，造成了無規律的垂向速度變化。第2階段是氣核從到水翼尾端位置遷移到距尾端水平距離為4倍弦長處。這一階段渦核具有相對較大的渦強，氣核隨渦核向下游段遷移過程中具有較為穩定的振蕩頻率和幅值。第3階段位于水平距離4倍弦長之后，在這一階段，渦核的強度逐步下降，而氣核的垂向速度變化頻率也隨之變緩慢。

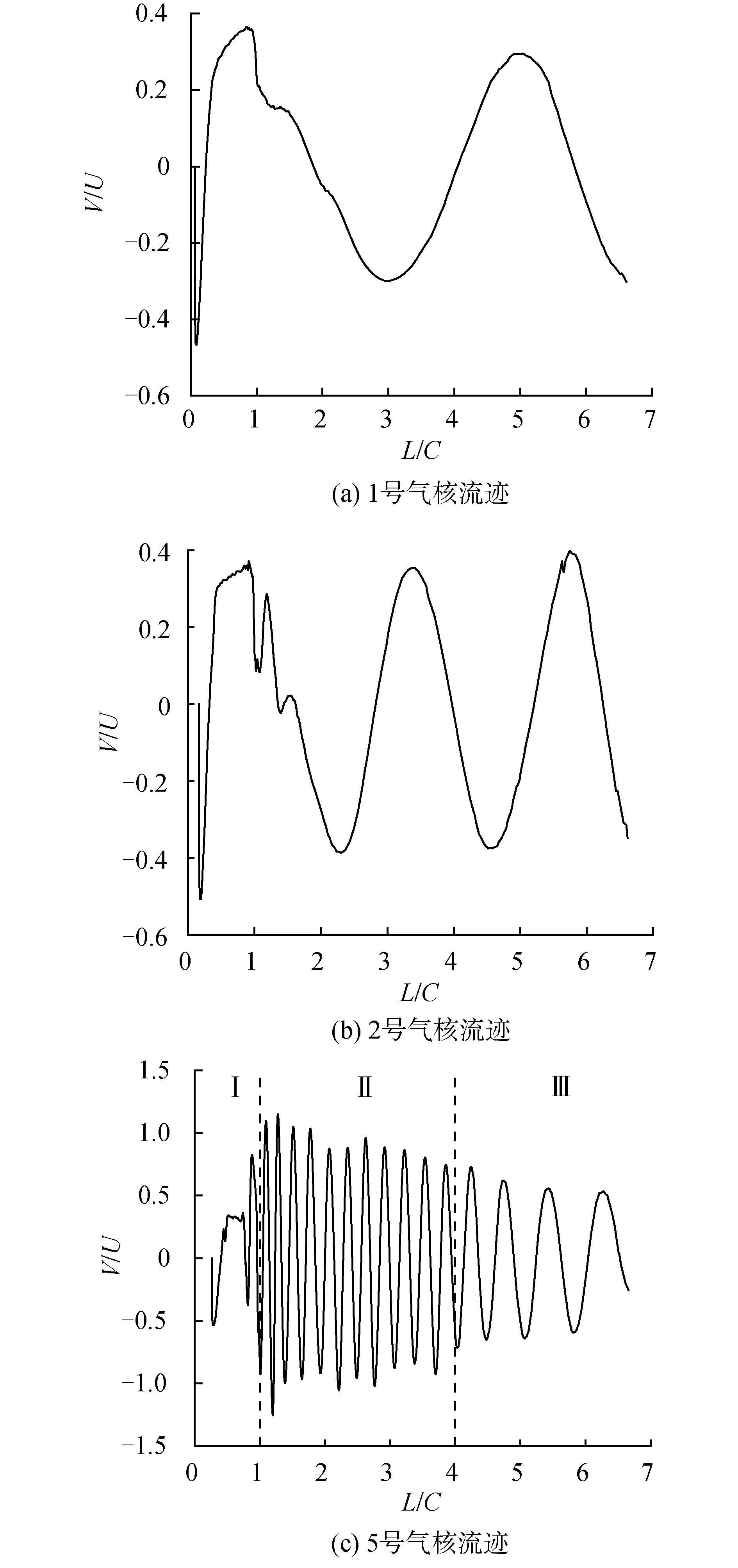
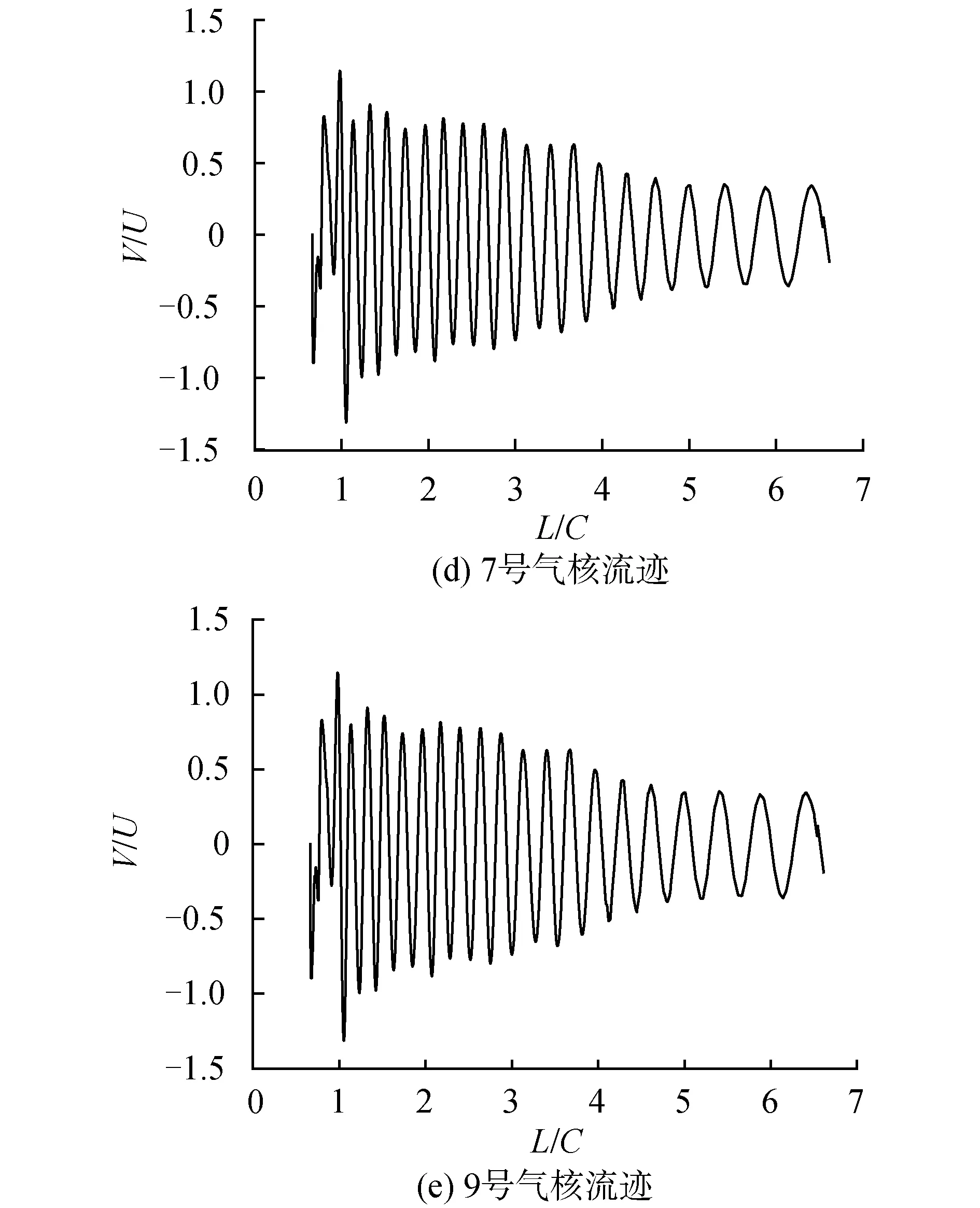
圖11 部分氣核流跡上的垂向速度分布Fig.11 Vertical velocity distribution in typical nuclei track

圖12中，(a)～(e)分別為1、2、5、7、9號的噴射器發射出的氣核運動過程中相對壓力的變化曲線。對遷移距離除以弦長得到L/C，對計算得到的相對壓力轉化為相對壓力系數Cp，完成無量綱化處理。壓力變化曲線與速度變化曲線有一定的相似之處，位于梢渦核心位置處和梢渦核心以外區域的流跡在壓力變化上具有2種明顯不同的趨勢。1號和2號的氣核在遷移過程中，壓力首先經歷了一段明顯的上升，在遷移到水翼后端1倍弦長的位置處相對壓力達到峰值；隨后下降到-0.3左右。而5、7和9號的氣核在遷移到水翼后端1倍弦長的位置處壓力先急劇下降，隨后再急劇上升，最后平穩上升。從氣核的遷移軌跡來看，1號和2號的氣核在剛開始遷移的過程中隨流線向展長的方向進行遷移，因而經歷了一次壓力上升；隨后被梢渦外端渦系捕獲后，壓力再次下降并穩定。而5、7、9號的氣核剛開始遷移時被渦核所捕獲，故而壓力急劇下降；隨后在隨渦核向后遷移的過程中，隨著渦強降低，壓力也隨之上升；而在渦強下降到一定程度后，下降趨勢逐步變慢，此時壓力上升趨勢也開始放緩。

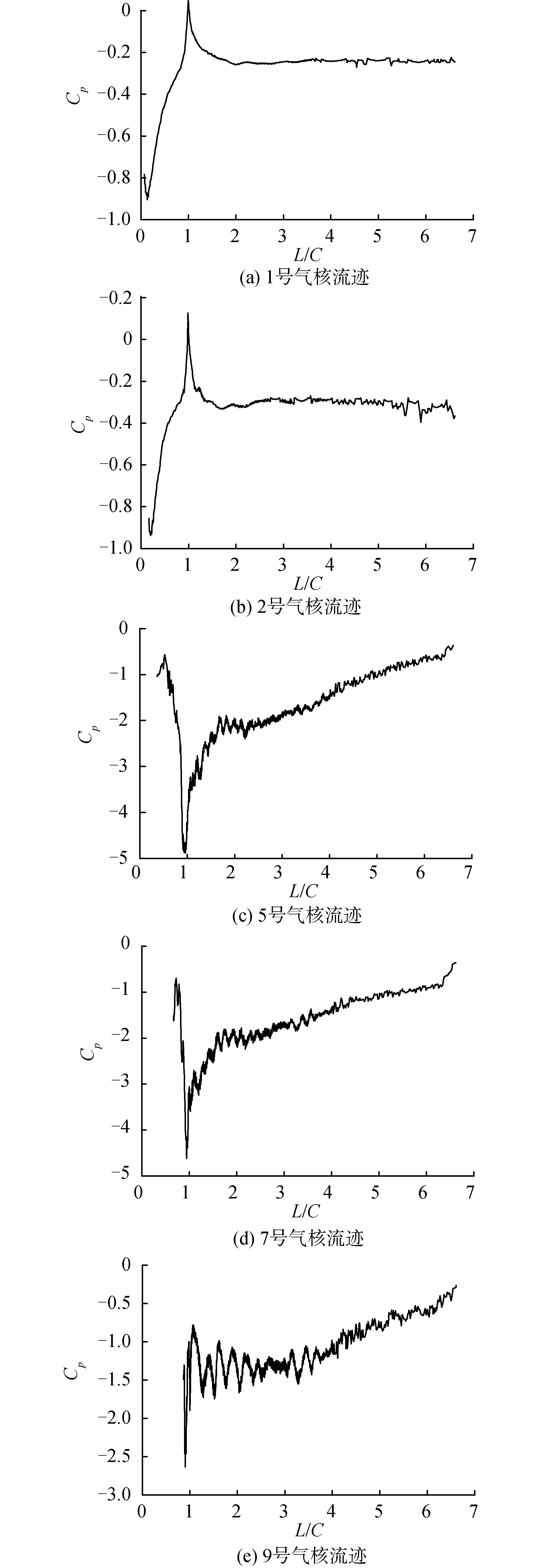
圖12 部分氣核流跡上的相對壓力分布Fig.12 Relative pressure distribution in typical nuclei track

3 結論

1)采用LES模型對帶導流罩的三維水翼受到的升阻力、無因次速度分布進行計算，與文獻中數據符合較好，計算結果具有良好的可信度。

2)帶導流罩的圓形導邊水翼的梢渦流場有著獨特的結構。在壓力面出現主渦和二次渦，在吸力面出現一系列小渦。主渦和二次渦在發展的過程中合并，形成梢渦核心，而吸力面形成的渦系在向后遷移的過程中，包裹在核心外部，形成總體的渦系。

3)氣核在遷移過程中，在水翼首部出現的氣核的遷移軌跡位于梢渦核心外，而水翼首部后端的氣核遷移軌跡位于梢渦核心內。此外，渦核會對氣核的遷移產生很大的影響，使其偏離流線的方向；氣核被渦核捕獲后，垂向速度會有較大的振蕩值，受到的壓力也會產生顯著的變化。