灌漿套筒連接裝配式梁柱節點精細有限元模型

羅小勇， 龍昊， 曹琨鵬

(1.中南大學 土木工程學院,湖南 長沙 410075； 2. 中南大學 湖南省裝配式建筑工程技術研究中心,湖南 長沙 410075)

鋼筋套筒連接裝配式混凝土結構因其結構簡單、施工方便，在裝配式結構構件的連接中運用得越來越廣泛。灌漿套筒連接混凝土結構由于存在先后澆混凝土結合面、構件連接處鋼筋用灌漿套筒替代的特征，抗震性能與傳統的現澆混凝土結構不同，國內外學者對其進行了大量的試驗和研究[1-8]。目前在對灌漿套筒連接裝配式結構進行數值模擬的試驗中，對于鋼筋套筒的模擬通常有2種方法：1)套筒全部采用實體單元建模方式[9-11]，該方法優點在于能較好地模擬套筒的實際受力情況，但需要定義各種材料和接觸面的類型，存在計算過程復雜且不容易收斂等缺點；2)默認套筒在連接部位的強度是可靠的[12]，僅把灌漿套筒部位模擬成鋼筋，該方法優點是易于操作，缺點是在建模過程中不僅忽略了套筒的實際受力，還忽略了套筒連接部位對整個裝配式構件受力時所產生的影響，所以模擬結果與試驗結果相差較大。除灌漿套筒有限元模擬之外，二次澆注混凝土不可避免地出現于后澆裝配式結構中，目前對后澆裝配式結構的數值模擬往往忽略了后澆混凝土結合面，后澆混凝土界面的力學性能對結構整體影響不容忽視。

本文通過對灌漿套筒連接鋼筋拉拔試驗結果進行了多因素線性統計分析，構建了在單軸拉伸下的本構關系，將此本構關系應用于灌漿套筒連接裝配式梁柱節點有限元模型中，并且考慮先后澆混凝土界面對節點模型的影響。結果表明數值模擬與試驗吻合良好，采用等效灌漿套筒本構關系建立的精細化有限元模型能較好地表征節點模型的抗震性能。

1 灌漿套筒鋼筋單向拉伸試驗及等效本構關系

1.1 單向拉伸試驗結果及分析

劉全威等[13]對26個套筒灌漿連接試件進行了拉拔試驗，選取了部分灌漿套筒應力應變曲線如圖1所示。灌漿套筒鋼筋連接試件在拉伸試驗中與鋼筋的拉伸試驗結果類似，都經歷了等效應力-應變呈線性增長、達到屈服階段和達到極限強度破壞的過程。表1為試驗中套筒灌漿連接件的性能參數，本文分析了試驗中可能對灌漿套筒連接本構關系的影響因素，考慮的試驗參數有鋼筋直徑d、套筒的長度L1、灌漿段的長度L2，套筒的外徑D1，套筒的內徑D2，鋼筋的屈服強度及鋼筋的極限強度，以該試驗結果為基礎提出灌漿套筒連接類似鋼筋的等效本構關系。

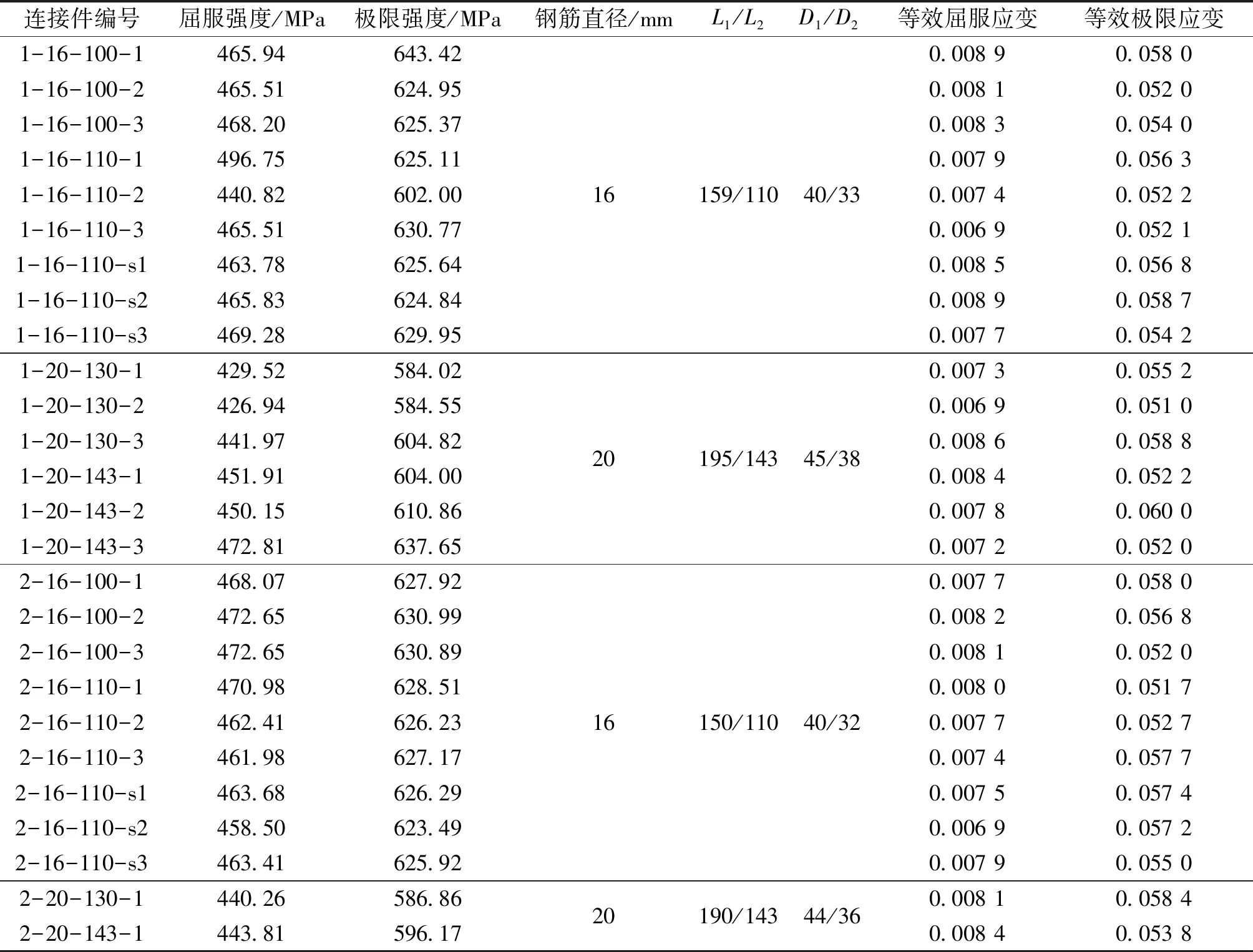
表1 套筒灌漿連接件的性能參數處理結果Table 1 The performance parameter processing results of grouted sleeve

圖1 灌漿套筒應力應變曲線Fig.1 The stress-strain curves of grouted sleeve

1.2 灌漿套筒鋼筋連接等效本構關系

基于灌漿套筒應力應變曲線所得的規律，灌漿套筒連接試件表現出與鋼筋類似的特性，故可選取類似鋼筋連接三折線本構模型模擬單向拉伸下灌漿套筒鋼筋連接本構關系，將試驗所得到的等效屈服點、等效屈服平臺結束點、等效極限荷載點統計于圖2中，其中A點與C點分別對應于灌漿套筒的等效屈服點與極限荷載點，AB段為灌漿套筒的屈服平臺。

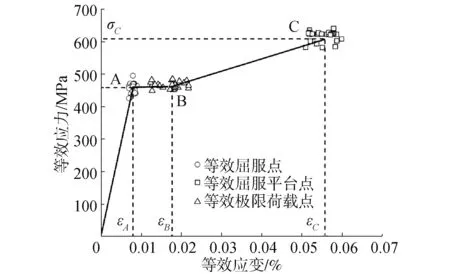
圖2 灌漿套筒連接三折線本構模型Fig.2 The trilinear constitutive model of grouted sleeve

1.3 特征點參數的取值

本文主要考察鋼筋錨固長度、屈服應變、鋼筋直徑、套筒總長度、鋼筋錨固長度、套筒外徑、套筒內徑、鋼筋直徑對灌漿套筒連接三折線本構模型的影響，使用統計學軟件SPSS對選用的本構模型特征點的應力應變各影響因素進行顯著性分析，分析結果如表2、表3所示。t值為回歸系數檢驗統計量，sig.為相伴概率值，特征點應力顯著性僅有鋼筋的屈服強度fy，并且特征點應力為鋼筋屈服強度的增函數。選擇鋼筋的屈服強度作為自變量進行多元回歸，所得結果如表4所示。擬合優度平方(R方)為0.668，統計量F=19.338，相伴概率值sig.=0.00，回歸比較顯著，得到擬合結果為：

σA=σB=-0.813fy+834.52

(1)

表5為各特征點應變的擬合結果，同理可得其余特征點的擬合結果為：

σC=0.367fy+396

(2)

εA=-0.369εy+6.983E-8L2+0.006

(3)

εB=-0.79εy+1.073E-5L2+0.04

(4)

εC=0.0369εy+0.38E-6L2+0.067

(5)

表2特征點的應力顯著性分析

Table2Thecharacteristicpointssignificanceanalysisofstress

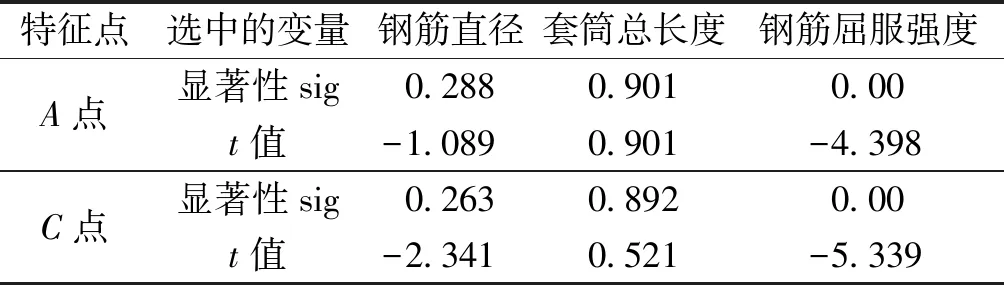
特征點選中的變量鋼筋直徑套筒總長度鋼筋屈服強度A點C點顯著性sig0.2880.9010.00t值-1.0890.901-4.398顯著性sig0.2630.8920.00t值-2.3410.521-5.339

注：顯著性sig與t值均為無量綱量。

表3特征點的應變顯著性分析

Table3Thecharacteristicpointssignificanceanalysisofstrain

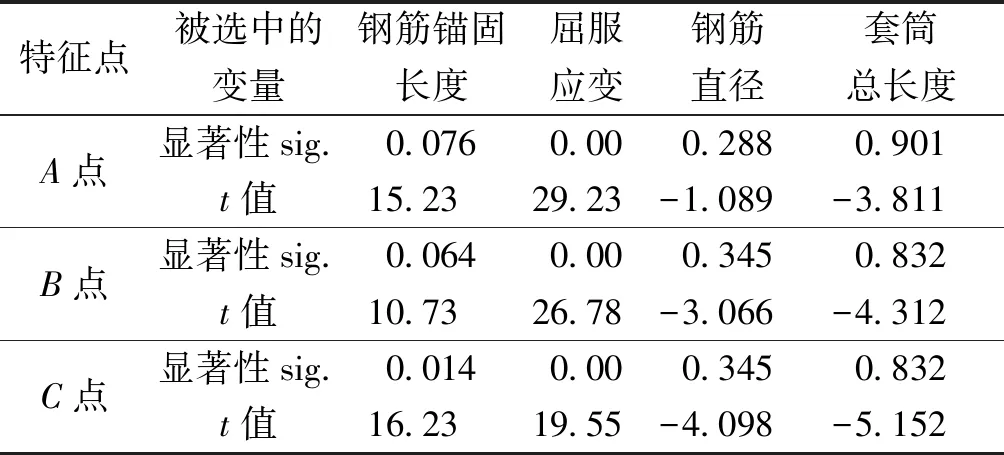
特征點被選中的變量鋼筋錨固長度屈服應變鋼筋直徑套筒總長度A點B點C點顯著性sig.0.0760.000.2880.901t值15.2329.23-1.089-3.811顯著性sig.0.0640.000.3450.832t值10.7326.78-3.066-4.312顯著性sig.0.0140.000.3450.832t值16.2319.55-4.098-5.152

注：顯著性sig與t值均為無量綱量。

表4 特征點應力的擬合結果Table 4 The stress fitting results of the characteristic points

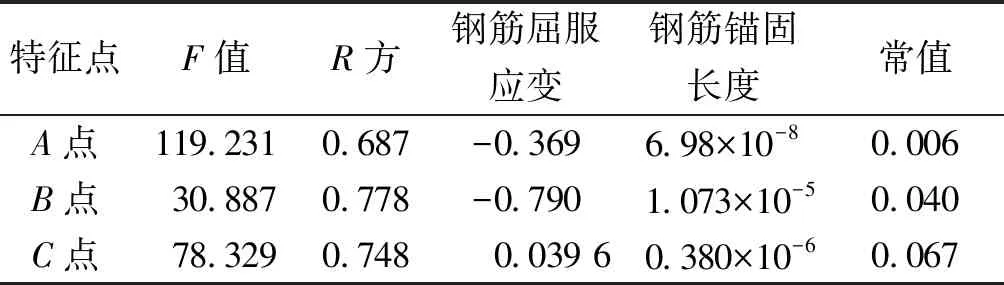
表5 特征點應變的擬合結果Table 5 The strain fitting results of the characteristic points

2 灌漿套筒連接裝配式梁柱節點有限元模型驗證

2.1 試驗概述

以文獻[14]中的灌漿套筒連接試件為驗證模型建立精細有限元模型進行對比，預制梁和柱端鋼筋均通過灌漿套筒進行連接，后澆混凝土形成整體，試件尺寸及配筋如圖3所示。設計軸壓比為0.3，預制構件混凝土設計強度等級為C30，后澆區混凝土設計強度等級為C40，梁柱縱向鋼筋均為HRB335，箍筋均為HPB300，具體力學性能參數如表6，試驗加載裝置如圖4所示，試件底部和頂部通過定向鉸連接，采用力和位移控制加載，在試件兩側的鋼筋混凝土梁端施加豎向往復荷載。試件屈服前，采用荷載控制進行加載，當試件達到屈服荷載時，采用位移控制循環加載。分析套筒灌漿后澆混凝土梁柱節點的破壞形態、變形能力、耗能能力、延性等指標。

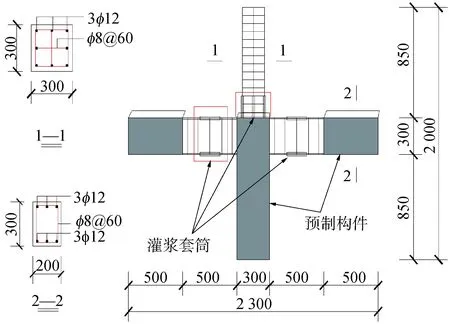
圖3 試件幾何尺寸及配筋Fig.3 The physical dimension and reinforcement of test pieces

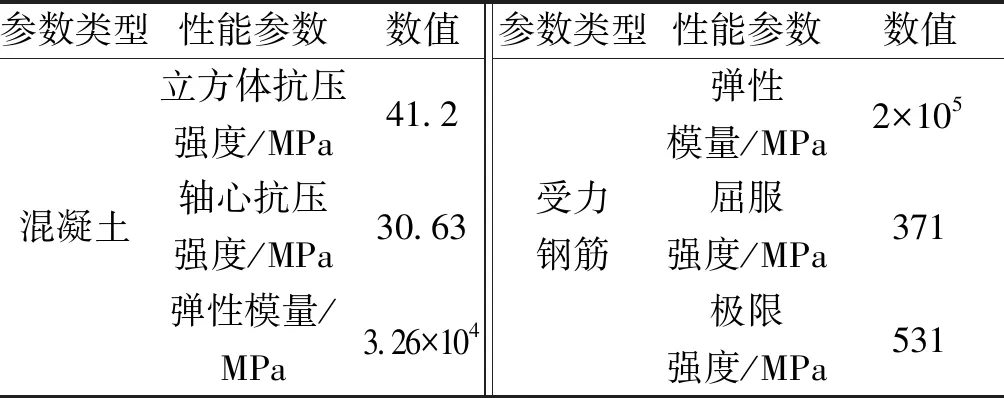
表6 材料力學性能指標Table 6 The mechanical properties

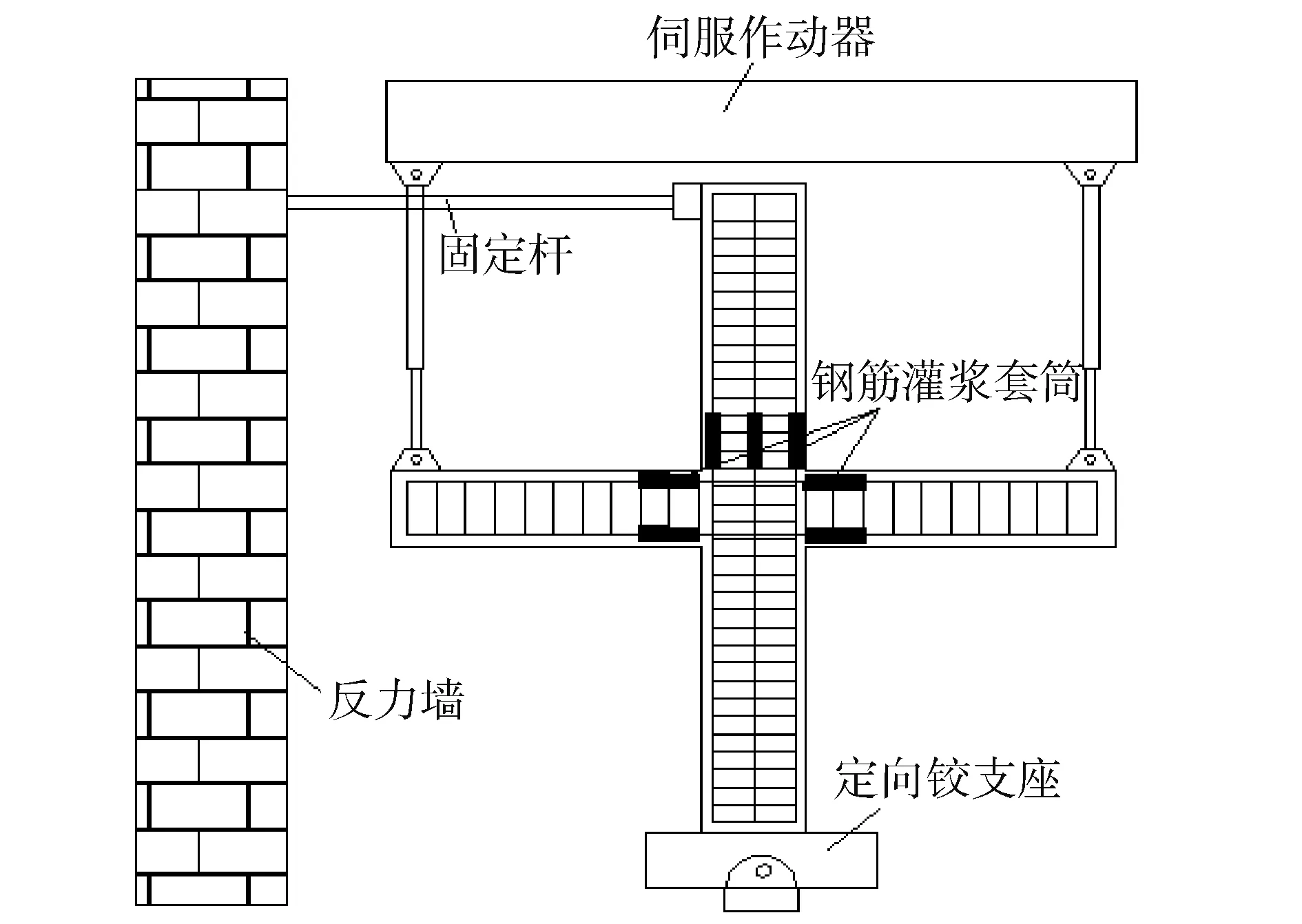
圖4 試驗加載裝置Fig.4 The loading device of test pieces

2.2 精細有限元建模

2.2.1 材料本構模型

混凝土本構采用ABAQUS自帶的混凝土損傷塑性模型。鋼筋本構選用雙折線模型，由彈性斜率段和塑性斜率段組成彈性斜率段的斜率為鋼材的彈性模量Es，塑性段斜率的斜率為0.01Es，采用材料試驗得出的屈服強度和極限強度。灌漿套筒本構模型采用前文提出的等效本構模型,如式(1)～(5)所示。

2.2.2 鋼筋混凝土粘結滑移

選擇Eligehausen模型[15]作為鋼筋混凝土粘結滑移本構，在ABAQUS中采用彈簧單元模擬鋼筋與混凝土之間的粘結滑移，沿鋼筋軸向的彈簧剛度依據Eligehausen模型中粘結應力-滑移曲線確定。鋼筋徑向的彈簧單元主要模擬消栓作用以及約束鋼筋單元節點與箍筋內部混凝土單元節點的豎直位移，對鋼筋混凝土之間的粘結滑移影響不大，沿鋼筋徑向彈簧剛度可以取鋼筋和混凝土彈性模量的極大值，本文每隔50 mm設置一組彈簧單元。

2.2.3 先后澆混凝土結合面模擬

劉健[16]研究表明先后澆混凝土界面的極限抗拉強度取混凝土極限抗拉強度的80%，達到極限抗拉強度80%后，承載力迅速下降到零，張銳[17]也對其進行了驗證。假設界面受壓為理想彈塑性，極限抗壓強度為混凝土的抗壓強度，達到極限強度后承載力能力保持不變。節點彈簧的法向力-位移關系如圖5所示。

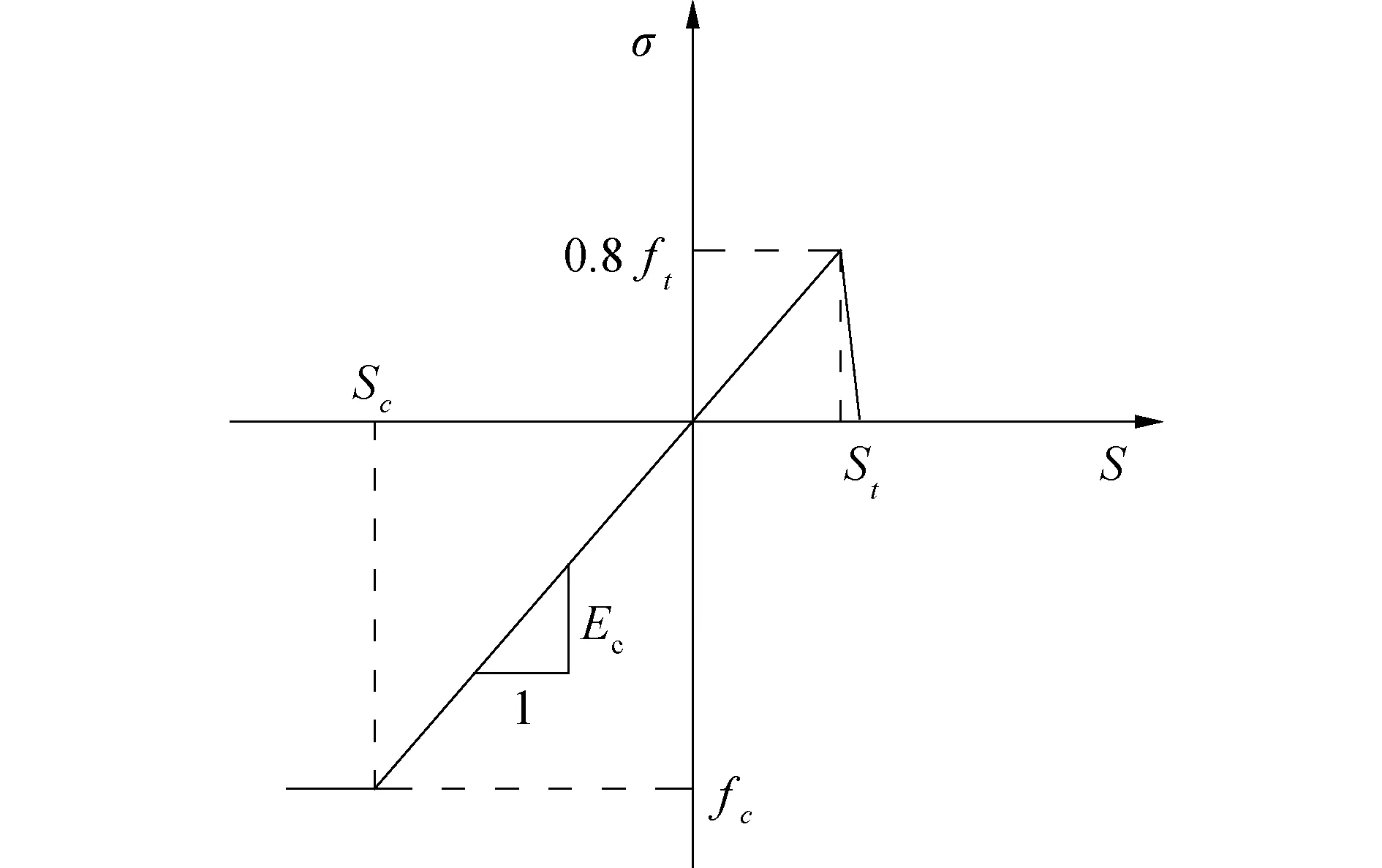
圖5 非線性彈簧法向力-位移關系Fig.5 The normal force-displacement of nonlinear spring

已有文獻對無側限先后澆混凝土界面抗剪強度進行了大量的試驗研究，先后澆混凝土界面剪切抗力主要由界面混凝土內部粘結力、由側限和界面凹凸產生的摩擦力、鋼筋的抗剪力3部分組成。范亮[18]綜合考慮影響界面抗剪強度的多個因素，建立了先后澆混凝土界面抗剪強度的計算公式，如式(6)表示，并且對大量試驗數據進行了回歸分析確定了其中的計算參數。通過式(6)代入試驗相關參數可得出節點彈簧的切向力-位移關系。在ABAQUS中通過定義界面彈簧模型的法向切向本構關系可以對先后澆混凝土結合面進行模擬。

(6)

2.2.4 單元選擇

本文中混凝土采用C3D8R實體單元，鋼筋采用T3D2桁架單元，套筒灌漿連接件用非線性彈簧Spring A模擬，通過非線性彈簧單元分別模擬界面的切向、法向受力情況，精細有限元模型如圖6所示。非線性關系通過各自的力-位(F-D)曲線來體現。F-D曲線通過先后澆混凝土界面的法向本構和切向本構計算。

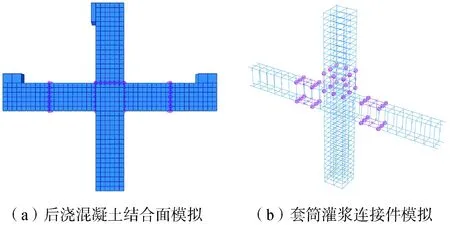
圖6 后澆混凝土結合面和套筒灌漿連接件模型Fig.6 Finite element model of concrete interface and grouted sleeve

2.3 套筒灌漿連接模擬驗證

2.3.1 破壞形態及裂縫發展

在低周反復荷載作用下的試件，加載初期梁柱節點核心區的受力符合拉壓桿模型，如圖7(a)，混凝土壓碎最早出現在核心區附近的梁端部，如圖7(b)，加載至開裂荷載時，由于梁端剛度分布不均勻，在套筒灌漿端部和梁柱交界面處出現豎向裂縫。壓碎后混凝土梁所分擔的外力急劇下降，結構受力主要由鋼筋骨架和混凝土柱承擔，梁柱節點核心區的受力不再是拉壓桿模型。繼續加載，裂縫逐漸向梁中擴展，當加載至30 kN時，梁端裂縫貫通，同時在核心區出現斜向裂縫。最后裂縫主要分布在梁柱相交界面位置，套筒灌漿兩端以及距離柱端500 mm截面位置。加載后期，在梁端混凝土屈服后，核心區箍筋受力急劇增加，開始屈服，如圖7(d)，最后峰值位移加載時，核心區箍筋基本都屈服，而梁的受力鋼筋應力較小，結構處于破壞階段，梁端混凝土發生壓潰破壞。有限元模擬可以很好地模擬出裂紋發展情況，與試驗所述破壞特征相同[14]，如圖8所示。

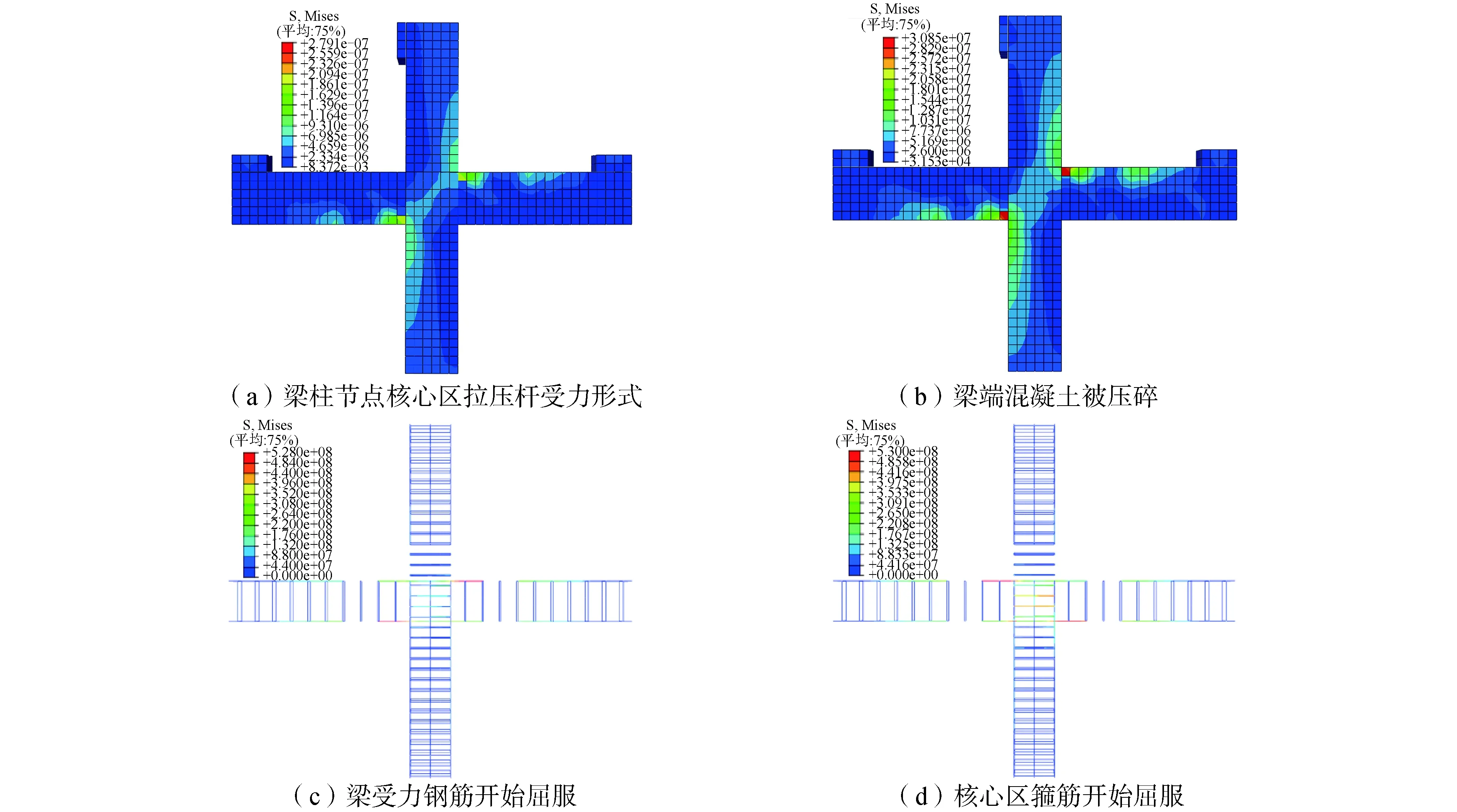
圖7 有限元模擬應力云圖Fig.7 Mises stress nephogram of the finite element simulation

2.3.2 承載力與延性

套筒灌漿連接裝配式混凝土結構梁柱節點試驗和有限元模擬的骨架曲線對比如圖9所示，骨架曲線上升段數值模擬結果與試驗結果吻合良好，數值模擬的初始剛度與峰值荷載與試驗結果接近，但在骨架曲線的下降段由于未考慮灌漿套筒的塑性損傷，數值模擬的承載力偏小。數值模擬的灌漿套筒連接后澆梁柱節點試驗與模擬的屈服荷載、屈服位移、峰值荷載、峰值位移、極限荷載、極限位移見表7，試件的位移延性系數根據極限位移Δu和屈服位移Δy之比計算，即μ=Δu/Δy。試件的有限元模擬結果和試驗結果的誤差在8%以內，結構的承載力可以有效模擬，其屈服荷載、峰值荷載、極限荷載模擬誤差分別是：7.11%、3.76%、4.72%，位移延性系數的誤差為7.84%，具有較好的參考意義，證明了所建立有限元模型的正確性。

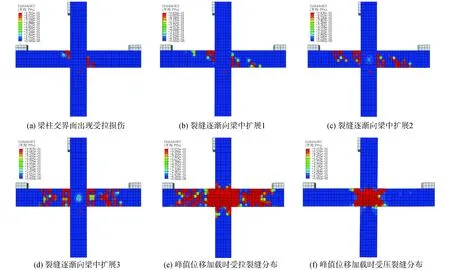
圖8 套筒灌漿連接后澆整體式梁柱節點有限元模擬裂紋發展結果Fig.8 The crackle developing of assembled reinforced concrete beam-column joints with grouted sleeves by finite element simulation

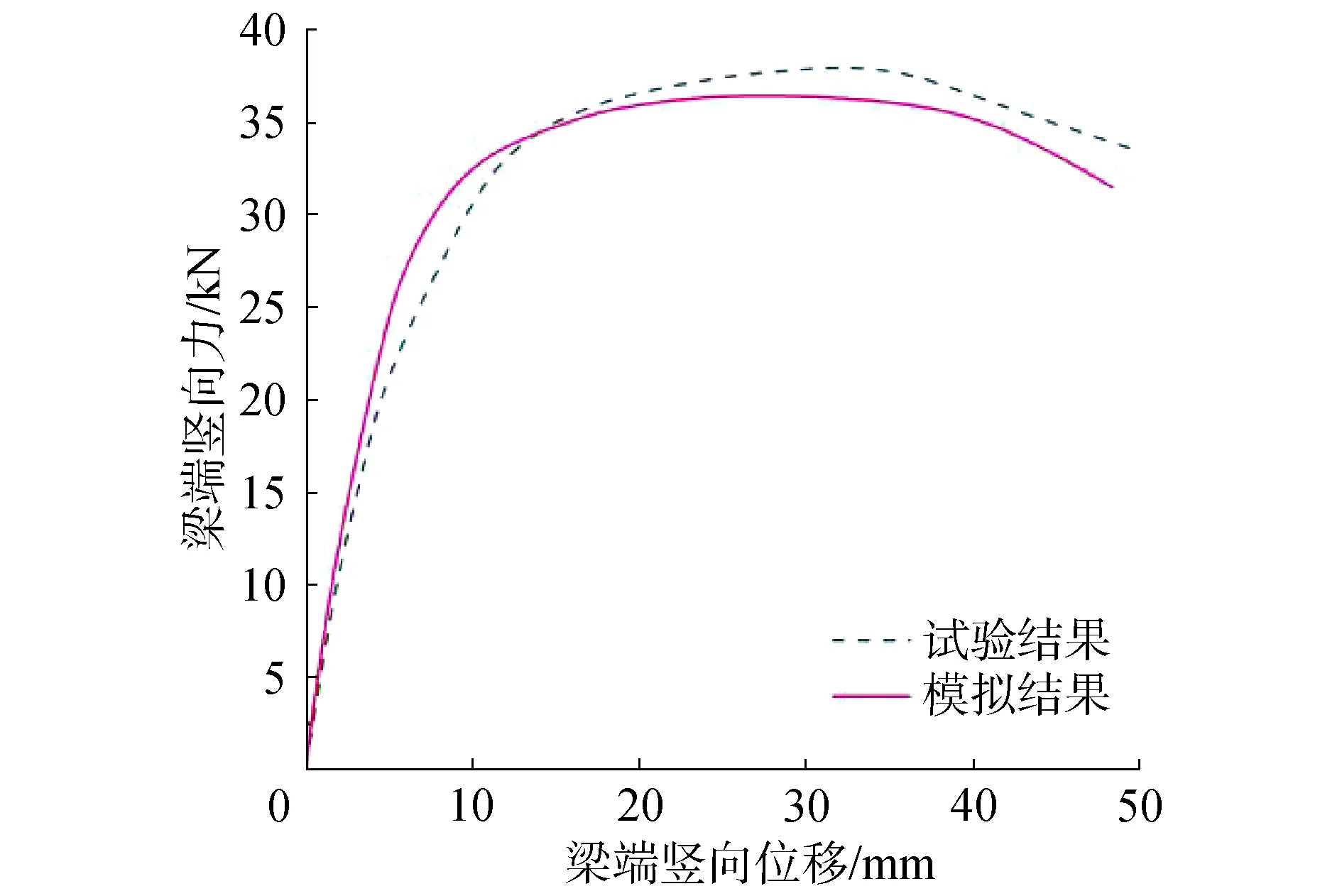
圖9 套筒灌漿連接后澆整體式梁柱節點的有限元分析骨架曲線Fig.9 The skeleton curve of assembled reinforced concrete beam-column joints with grouted sleeves by finite element simulation

2.3.3 荷載-位移滯回曲線

套筒灌漿連接混凝土結構后澆整體式梁柱節點試驗和有限元模型的滯回曲線對比如圖10所示，結果見表8，有限元模擬結果與試驗滯回曲線結果較為接近，均比較飽滿，說明灌漿套筒連接裝配式梁柱節點具有良好的耗能能力。

由于模擬套筒的彈簧單元和鋼筋桁架單元在ABAQUS中無法定義循環荷載下的本構關系，正向加載時，有限元模擬結果比試驗結果最大承載力小3.76%，反向加載時的滯回曲線所包圍的面積較小，有限元模擬結果比試驗結果最大承載力小13.23%,正向加載時的誤差小于負向加載。加載后期，有限元模型因為考慮了粘結滑移效應，滯回環和試驗試件相似，趨向于弓形，由表8滯回環面積比值可以看出在臨近破壞時構件耗能能力的誤差較小。

表7套筒灌漿連接后澆整體式梁柱節點的試驗結果和模擬結果對比

Table7Theresultcomparisonbetweenthesimulationandexperiment

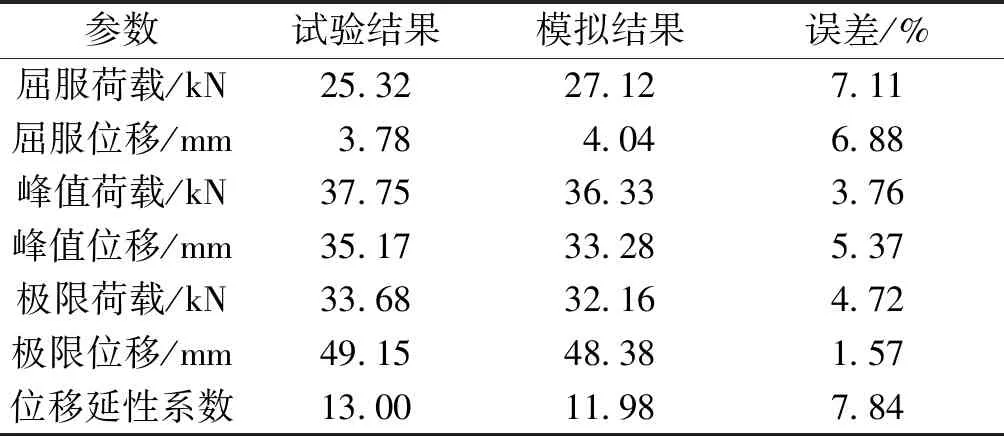
參數試驗結果模擬結果誤差/%屈服荷載/kN25.3227.127.11屈服位移/mm3.784.046.88峰值荷載/kN37.7536.333.76峰值位移/mm35.1733.285.37極限荷載/kN33.6832.164.72極限位移/mm49.1548.381.57位移延性系數13.0011.987.84

注：因為骨架曲線未下降至最大承載力的85%，本文取承載力下降至最大承載力的90%時所對應的位移作為極限位移。

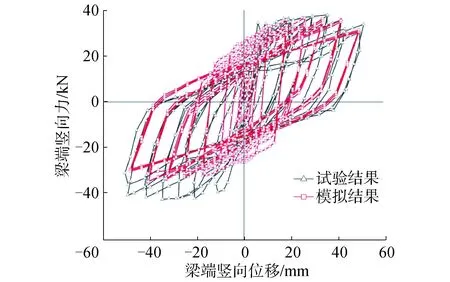
圖10 套筒灌漿連接后澆整體式梁柱節點試驗和有限元模擬的滯回曲線對比Fig.10 The hysteretic curve comparis between the simulation and experiment

表8套筒灌漿連接后澆整體式梁柱節點試驗和有限元的耗能能力對比

Table8Theenergydissipationcapacitybetweenthesimulationandexperiment

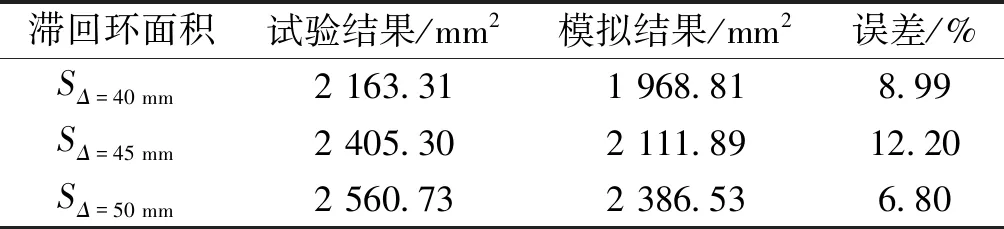
滯回環面積試驗結果/mm2模擬結果/mm2誤差/%SΔ=40 mm2 163.311 968.818.99SΔ=45 mm2 405.302 111.8912.20SΔ=50 mm2 560.732 386.536.80

注：SΔ=40 mm、SΔ=45 mm、SΔ=50 mm分別表示表示第一次位移加載到40 mm、45 mm、50 mm時滯回環的面積，表征耗能能力。

2.3.4 灌漿套筒接頭處的應變

圖11為灌漿套筒接頭受拉狀態時，循環荷載最大時的應變值，圖中δ為加載的位移，δy為屈服位移。

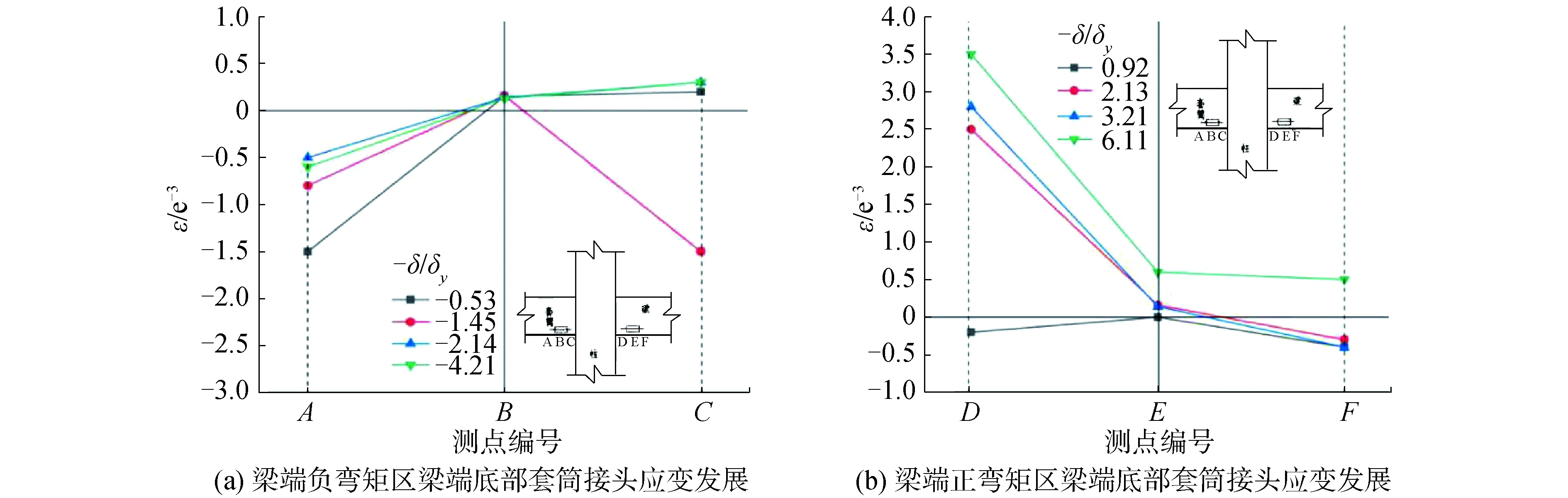
圖11 梁端灌漿套筒接頭應變值Fig.11 Rebar strain of grouting coupler

在加載初期，灌漿套筒軸向應變及灌漿套筒兩端的鋼筋應變基本相同。由于灌漿套筒截面的剛度較大，荷載從梁端經過灌漿套筒截面傳遞給鋼筋，灌漿套筒接頭兩端的鋼筋發生屈服，隨著加載時間增長，靠近節點核心區的應變(測點C和測點D)灌漿套筒兩端應變明顯增加，導致梁端彎矩較大截面處應變增大，而灌漿套筒始終處于彈性階段，灌漿套筒的受力情況也與試驗所得結論相同。

3 結論

1)通過灌漿套筒連接試件單調拉伸試驗所得的數據進行歸類、分析，構建了其在單向拉伸情況下的等效本構模型，用統計分析軟件得出了影響該本構模型的影響因素，灌漿套筒應力與鋼筋的屈服強度顯著相關，應變與鋼筋的屈服應變以及鋼筋的錨固長度顯著相關，并給定了相關影響因素的參數取值；

2)有限元模型裂縫開展形態、開展歷程、試件破壞模式、灌漿套筒在加載過程中的受力情況與試驗結論大致相同，驗證了套筒灌漿連接件等效本構的正確性以及模擬方法的科學性；

3)有限元模型與試驗模型加載過程中的屈服荷載、峰值荷載、極限荷載模擬誤差很小，分別是7.11%、3.76%、4.72%，且結構臨近破壞時骨架曲線開始出現下降段，和試驗現象一致；

4)有限元模擬滯回曲線和試驗試件相似，趨向于弓形，體現耗能能力的滯回環的包絡面積誤差也在13%以內，在加載后期，由于無法定義套筒的塑性損傷，導致存在一定的誤差；

5)本文提出的利用非線性彈簧單元定義提出的等效本構方法進行有限元模擬不僅極大地簡化了計算時間，同時還有效地規避了較為繁瑣的套筒建模及產生的不收斂情況，具有一定的適用性。