基于虛擬陣元信號重構的嵌套陣穩健波束形成

盧 建, 楊 劍, 侯 博, 余志勇, 劉光斌

(火箭軍工程大學導彈工程學院, 陜西 西安 710025)

0 引 言

自適應波束形成技術通過空域濾波處理能夠大幅提高陣列天線的輸出信干噪比(signal to interference plus noise ratio, SINR),廣泛應用于雷達、聲吶、無線通信、射電天文學等眾多領域,發揮著日益重要的作用[1-2]。通常情況下,自適應波束形成技術的研究都是針對陣元間距在半波長以內的均勻陣列,由于陣列天線的自由度和空間分辨率要求更多的天線陣元和更大的陣列孔徑,但是硬件成本約束和計算復雜度限制了陣元數目的進一步增加[3-4]。因此,在陣元數量有限的約束條件下,為有效擴展陣列天線孔徑,以互質陣和嵌套陣為代表的非均勻陣列的研究正引起廣泛的興趣。

目前,對于互質陣和嵌套陣的研究主要是通過對采樣協方差矩陣的向量化操作得到高維度的陣列接收信號,用于波達方向(direction of arrival, DOA)估計,通過引入虛擬陣元能夠有效提高陣列的自由度和空間分辨率[5]。對于互質陣的自適應波束形成技術研究已經取得部分成果[3,6-8],但是基于嵌套陣的波束形成技術研究成果很少,且技術路線相對單一。文獻[9]通過建立差分合成陣利用稀疏表示方法進行DOA估計,然后重構陣列接收信號的干擾加噪聲協方差矩陣(interference plus noise covariance matrix, INCM)獲取波束形成的權矢量。然而,該方法需要大量的采樣快拍數才能達到較好的干擾抑制能力。文獻[10]提出向前向后空間平滑的數據協方差矩陣重構方法用于嵌套陣的波束形成。文獻[11]首先向量化采樣協方差矩陣,然后通過空間平滑構建高維的均勻陣列的協方差矩陣,從而獲取波束形成權矢量。文獻[12]首先向量化采樣協方差矩陣,然后構建Toeplitz矩陣代替采樣協方差矩陣計算波束形成的權矢量。然而,以上算法均沒有考慮消除采樣信號協方差矩陣中包含的期望信號成分對波束形成器性能的影響,在高信噪比(signal to noise ratio, SNR)條件下將引起期望信號的“自消”現象。文獻[13]對向量化采樣協方差矩陣和空間平滑構建的高維協方差矩陣進行特征分解,提取主要特征向量用于獲取向量化的INCM,一定程度上消除了期望信號的影響。但是,在高SNR條件下,該算法重構的INCM精度降低,仍然可能導致期望信號的“自消”。文獻[4]首先通過Capon空間譜計算嵌套陣列的INCM,然后向量化處理再構建Toeplitz矩陣,并且增加了對期望信號的DOA估計,使得波束形成器性能有進一步提升。綜上所述,目前對于嵌套陣的波束形成技術研究主要是通過向量化采樣協方差矩陣以不同的方式構建高維度的協方差矩陣來實現的,但是這類方法的收斂速度慢,需要大量的采樣快拍數才能達到良好的抗干擾性能,并且對同一場景中不同強度的干擾信號抑制能力差。因此,需要進一步研究嵌套陣的波束形成技術,實現收斂速度快、綜合抗干擾能力強的目標要求。

基于以上分析,本文在信號DOA估計的基礎上,通過重構虛擬陣元接收的干擾信號和估計信號功率,構建高維度的虛擬均勻陣列的INCM和接收數據,獲取的權矢量可直接應用于虛擬陣列的波束形成處理。

1 信號模型

圖1 嵌套陣結構圖

那么,在k時刻嵌套陣的接收信號可表示為

x(k)=As(k)+n(k)

(1)

(2)

式中,K表示采樣信號快拍數。那么,自適應波束形成器的輸出可表示為

y(k)=wHx(k)

(3)

式中,w=[w0,w1,…,wN+M-1]T表示波束形成器的權矢量。為了得到最優的波束形成器權矢量,可使輸出SINR最大,即

(4)

(5)

2 算法描述

通常情況下,干擾信號強度是遠大于噪聲的,因此利用空間譜估計方法精確地估計其來波方向是可以實現的。本文擬通過對干擾信號的DOA估計,重構外部均勻陣列2中“空洞”處虛擬陣元接收的干擾信號,從而構建一個虛擬的稠密均勻陣列,如圖2所示,其中虛線空心圓圈表示將要重構的虛擬陣元。然后,通過估計信號功率,重構虛擬的均勻陣列的INCM,從而可得到波束形成器的權矢量。

圖2 虛擬的稠密陣列結構圖

2.1 信號DOA估計

x3(k)=[x0(k),x1(k),…,xN(k)]T

(6)

相應地,接收信號的導向矢量可表示為

a3(θq)=[e-j2πp1dw-1sin θq,e-j2πNdw-1sin θq]T

(7)

則均勻子陣3的采樣數據協方差矩陣可表示為

(8)

(9)

由于期望信號SNR的動態變化范圍較大,在極低SNR條件下,由于干擾信號的影響,通過MUSIC方法可能無法在角度區間Θ范圍內搜索到有效的峰值。因此,可單獨采用Capon空間譜估計期望信號來波方向,即

(10)

2.2 重構虛擬陣元接收的干擾信號

由圖2所示的陣列結構可知,要使整個陣列構成一個虛擬的均勻線陣,需要重構外部均勻線陣2中虛擬陣元的接收信號,其位置矢量可表示為dpv=d[N+1,N+2,…,M(N+1)-2]T,因此各虛擬陣元接收的干擾信號可分別表示為

(11)

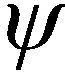
(12)

那么,信號矢量s(k)的估計值[16-17]可通過下式計算得到:

(13)

(14)

根據式(12)～式(14)可得,該方法可通過矩陣運算估計多個連續快拍數的虛擬陣元接收信號,因此算法具有較高的計算效率。

2.3 虛擬均勻陣列的自適應波束形成

(15)

(16)

(17)

(18)

(19)

(20)

因此,根據式(3),可得虛擬均勻陣列的波束形成輸出表示為

(21)

2.4 算法流程

本文所提算法的主要步驟可歸納如下:

步驟3利用式(17),可估計信號功率,通過式(18)重構虛擬均勻陣列的INCM;

步驟6根據式(21)可得到波束形成器輸出結果。

3 仿真分析

為了驗證所提算法的有效性,在仿真過程中,設定嵌套陣中內部子陣1和外部子陣2的陣元數分別為N=5和M=5,噪聲建模為一個均值為0方差為1的圓對稱復高斯隨機過程。假設期望信號的入射角度為θ0=10°,兩個干擾信號的來波方向分別為θ1=-30°和θ2=45°。當比較輸出SINR隨輸入SNR變化時,采樣快拍數設置為K=70;當比較輸出SINR隨采樣快拍數變化時,期望信號的SNR設置為10 dB,并且以上兩種情況下的INR均設置為INR=35 dB。對以下每個場景的仿真,都是以200次獨立的蒙特卡羅試驗的平均值作為結果輸出。

在仿真過程中,將所提算法與多個自適應波束形成算法進行了性能對比,包括,文獻[4]提出的使用嵌套子陣的穩健高效自適應波束形成(nested subarray-robust and efficient adaptive beamforming，NS-REAB), 文獻[10]提出的向前向后空間平滑波束形成(forward backward spatial smoothing, FBSM),文獻[12]提出的基于擴張協方差矩陣的波束形成(augmented covariance matrix for digital beamforming, ACM-DBF),文獻[11]提出的基于空間平滑的最小方差無失真響應算法(spatial smoothing method for minimum variance distortionless response, SSM-MVDR),文獻[20]提出的最差性能最優法(worst-case performance optimization, WCPO),文獻[21]提出的基于INCM重構和導向矢量估計的波束形成算法(interference covariance matrix reconstruction and steering vector estimation, ICMR-SVE)。在WCPO算法中,參數設置為ε=0.3,所提算法中譜峰搜索間隔和ICMR-SVE算法中的Capon積分間隔均設置為0.1°。所有參與測試波束形成算法中涉及的期望信號角度區間設置為Θ=[θ0-3°,θ0+3°]。

3.1 DOA估計誤差的影響

在第1個實驗中,考慮信號的DOA估計誤差對所提波束形成算法性能的影響。假設兩個干擾信號的來波方向θ1和θ2分別在[-35°,-25°]和[40°,50°]范圍內隨機變化,期望信號來波方向θ0=10°且保持不變。采用均方根誤差(root mean square error, RMSE)作為DOA估計性能的量化指標,具體定義為

(22)

圖3 DOA估計誤差對性能的影響

為了分析DOA估計誤差對所提波束形成算法性能的影響,分別獨立地仿真波束形成器輸出SINR在一定期望信號和干擾信號DOA估計誤差條件下的性能變化曲線。在仿真過程中,設定期望信號的DOA估計RMSE分別為0.6°,1.2°，1.8°;干擾信號的DOA估計RMSE分別為0.05°,0.1°，0.15°。注意,每個干擾信號的DOA估計誤差隨機分布,且每次仿真實驗中僅存在一種信號的誤差。如圖3(b)所示,給出了在特定DOA估計誤差條件下,與最佳輸出SINR的偏差隨輸入SNR的變化曲線。從仿真結果可知,所提算法性能受干擾信號DOA估計誤差影響較大,但是由于干擾信號強度通常遠大于噪聲,當INR大于20 dB時,DOA估計的RMSE小于等于0.05°,造成輸出SINR損失小于1.2 dB, 并且隨著采樣快拍數的增加,其影響將進一步減小。

3.2 干擾信號DOA誤差

在第2個實驗中,主要考察干擾信號的DOA誤差對波束形成器輸出SINR的影響。假定期望信號來波方向θ0=10°已知且保持不變,仿真過程中干擾信號誤差服從[-5°,+5°]范圍內的均勻分布,但在每次實驗中的采樣快拍之間保持不變,而在各次實驗之間隨機變化。

如圖4(a)和圖4(b)所示,分別展示了波束形成器輸出SINR對應輸入SNR和采樣快拍數的變化曲線。從仿真結果可知,所提方法與ICMR-SVE算法性能相似,都非常接近最優輸出SINR,且性能明顯優于其他測試算法。

圖4 干擾信號方向誤差影響

3.3 所有信號DOA誤差

在第3個實驗中,主要研究期望信號和干擾信號同時存在的DOA誤差對波束形成器性能的影響。通常期望信號的來波方向具備一定的先驗知識,可合理假定期望信號的方向誤差服從[-2.5°,+2.5°]范圍內的均勻分布,而干擾信號的方向誤差服從[-5°,+5°]范圍內的均勻分布,所有信號來波方向在每次仿真采樣快拍之間保持不變,在各次仿真實驗之間隨機變化。

仿真結果如圖5(a)和圖5(b)所示,當期望信號DOA存在誤差時,所提出的波束形成算法在輸入SNR低于0 dB時,由于期望信號DOA估計誤差的影響,其性能與ICMR-SVE算法相近,而優于其他參與測試的算法;隨著輸入SNR的升高,所提算法的輸出SINR幾乎等于最優值。同時圖5(b)表明,當采樣快拍數超過70時,所提算法的輸出SINR與最優波束形成器相近,其收斂速度明顯優于其他方法。

圖5 信號方向誤差影響

3.4 不同強度干擾信號

在第4個實驗中,主要考察波束形成器同時處理不同強度干擾信號的能力。假設期望信號的來波方向為θ0=10°,其輸入SNR設置為10 dB,3個不同強度的干擾信號來波方向分別為θ1=-30°,θ2=45°和θ3=30°,其INR分別設置為30 dB,20 dB和35 dB。仿真過程中,所有信號方向保持不變且未知。

圖6(a)和圖6(b)分別是波束形成器輸出SINR隨著輸入SNR和采樣快拍數的變化曲線。由圖6(a)可知,所提算法性能與最優波束形成器相似,且明顯優于參與測試的其他算法。圖6(b)表明,所提算法能夠以最快的速度收斂,當采樣快拍數超過60時,即可達到最優性能。相比其他算法,由于采用向量化采樣協方差矩陣的方式,算法收斂速度慢,當采樣快拍數較少時,波束形成器輸出SINR的增幅較小。

圖6 不同強度干擾信號影響

3.5 抗主瓣相近干擾性能

在第5個實驗中,主要驗證主瓣相近干擾條件下(即干擾信號與期望信號來波方向相近)波束形成器的抗干擾性能。假設添加一個靠近主瓣的干擾信號,其信號來波方向為θ3=6.5°,輸入INR為35 dB,其他信號相應參數保持不變,所有信號的來波方向未知。注意,該仿真實驗的采樣快拍數設置為K=150。

仿真結果如圖7(a)和圖7(b)所示,隨著輸入SNR和采樣快拍數的變化,所提算法的性能始終保持最優,甚至優于最優波束形成器。這主要是因為嵌套陣屬于稀疏陣列,其最優波束形成器的主瓣展寬,旁瓣升高,當干擾信號與期望信號來波方向相近時,將引起波束指向偏移,導致其抑制主瓣相近干擾性能明顯不足。而所提算法通過虛擬陣元構建了一個連續的均勻陣列,使得波束形成器的自由度大幅提高,波束主瓣變窄,旁瓣降低,零陷加深,能夠在一定角度范圍內有效抑制稀疏陣列靠近主瓣的干擾信號,且干擾抑制能力更強。

圖7 主瓣干擾影響

3.6 非相干局部散射

在第6個實驗中,主要考察非相干局部散射對波束形成器輸出SINR性能的影響。假設期望信號擁有一個時變的導向矢量,具體表示為

(23)

(24)

式(24)取最大值時的權矢量可通過下式計算[21-22]:

(25)

式中,P{·} 表示取矩陣的最大特征值所對應的特征向量。

如圖8(a)和圖8(b)所示,分別是波束形成器輸出SINR對應輸入SNR和采樣快拍數的變化曲線圖。從以上仿真結果可知,通過虛擬擴展,波束形成器的自由度得到大幅增加,抗干擾能力明顯增強,所提算法抗干擾性能優于所有參與測試的其他方法,并且隨著采樣快拍數的增加,輸出SINR與最優波束形成器性能相近。

圖8 信號非相干局部散射影響

4 結 論

本文提出了一種基于虛擬陣元信號重構的嵌套陣穩健波束形成算法,通過估計信號來波方向,對虛擬陣元接收的干擾信號進行重構,從而構建一個虛擬的稠密均勻陣列。在估計信號功率的基礎上,重構虛擬稠密均勻陣列的INCM,從而得到波束形成器的權矢量,并且給出了應用波束形成權矢量處理虛擬陣列接收信號的實現方法。仿真實驗表明,所提算法能夠有效克服信號DOA誤差和不同強度干擾信號的影響,且收斂速度快。通過構建虛擬的稠密均勻陣列,所提波束形成算法的自由度得到大幅增加,使得波束主瓣寬度變窄,旁瓣降低,零陷加深,柵瓣得到有效抑制,能夠在一定角度范圍內抑制嵌套陣列靠近主瓣的干擾,且對信號的非相干局部散射保持良好的穩健性。