基于偏置比例導引的落角約束滑模制導律

王曉海, 孟秀云, 周 峰, 邱文杰

(1. 北京理工大學宇航學院, 北京 100081; 2. 北京航天自動控制研究所, 北京 100039)

0 引 言

精確制導武器在現代戰爭中占據著不可替代的位置。隨著科學技術的發展,裝甲車輛、艦船等目標的防御能力相較于以往有了顯著的提高。為獲得更好的打擊效果,要求飛行器以某種角度命中目標[1]。1969年,帶終端落角約束的制導理論在阿波羅計劃首次登月時得到了應用[2]。Kim等[3]在機動彈頭制導問題中首次考慮落角約束問題。文獻[4]提出了一種制導律,根據終端落角要求計算幾何圓弧彈道,之后給出控制指令使導彈跟蹤計算出的圓弧彈道。文獻[5]基于非奇異快速終端滑模和二階滑模控制理論,提出了一種帶落角約束的有限時間滑模制導律。文獻[6]以攻角作為控制指令,運用滑模變結構理論推導了滿足終端攻擊角度約束和攻角約束的制導律。文獻[7]提出了一種偽機動比例導引律,并設計了自適應參數,降低了初始過載。文獻[8]推導了一種帶落角約束的無奇點快速終端滑模制導律,并設計了非線性擾動觀測器對擾動進行動態補償。文獻[9]提出了一種考慮加速度飽和的落角約束制導律,并將目標加速度信息作為擾動進行觀測補償。文獻[10]提出了一種基于落角約束的偏置比例導引律,并設計了盲區控制方案,減小了命中點處的法向過載。文獻[11]基于飛行力學原理和最優控制理論提出了一種落角約束最優制導律。文獻[12]基于二階滑模理論提出了一種有限時間收斂的落角約束制導律,并引入二階觀測器來對目標運動進行估計。文獻[13]基于李雅普諾夫穩定性理論提出了一種兩階段落角約束導引律。文獻[14]設計了一種落角約束滑模制導律,并應用模糊控制理論與徑向基函數(radical basis function, RBF)神經網絡理論,對導引律系數進行自適應調節。文獻[15]基于反饋線性化與有限時間控制理論推導了針對固定目標的落角約束制導律。文獻[16]考慮視場角約束的限制,基于追蹤法與比例導引法設計了滿足攻擊角約束的制導律。文獻[17]從實際物理意義的角度對帶落角約束的最優制導律進行了分析,并推導了一種新形式的最優制導指令。文獻[18]基于自適應反步法推導了針對運動目標的含攻擊角約束的制導律,并提出了一種平滑二階滑模微分器,對虛擬控制率的微分進行估計。文獻[19]基于滑模控制理論和反步法,并考慮自駕儀動力學,設計了一種帶攻擊約束的魯棒制導律,并設計了自適應二階滑模觀測器對目標機動信息進行估計。文獻[20]基于雙曲正切函數設計了有界虛擬制導律,之后引入映射,控制垂直于彈目視線的相對速度,對虛擬制導律進行跟蹤,得到了帶攻擊角約束的制導律。文獻[21]提出了一種新型的非奇異終端滑模制導律。文獻[22]設計了一種自適應快速固定時間滑模制導律,可以從任何初始角度以期望的攻擊角擊中目標。文獻[23]提出了一種由觀測階段和攻擊階段組成的兩階段最優制導律,并將最優制導律與切換項結合,使之能夠滿足攻擊角約束和視場角約束。文獻[24]基于二階滑模設計了一種考慮駕駛儀動力學的攻擊角約束制導律,并使用反步法設計滑模面,有效消除了抖振。文獻[25]基于非均勻快速終端滑模面理論和二階滑模控制理論,設計了滿足攻擊角約束的具有耦合項的非奇異快速終端三維二階滑模導引律。文獻[26]考慮執行機構飽和問題,并基于制導控制一體化設計了一種滿足攻擊角約束的制導律。文獻[27]針對運動目標提出一種攻擊角約束的制導律,該制導律分為兩個階段,第一個階段采用非奇異終端滑模制導律使導彈在有限時間內以期望的攻擊角攻擊虛擬目標,第二個階段使用比例導引法,使導彈以恒定的航跡角攻擊目標。文獻[28]重點考慮剩余飛行時間估計問題,并針對基于終端滑模控制的攻擊角約束制導律,提出了一種剩余飛行時間估計方法。文獻[29]基于非奇異終端滑模控制理論提出了一種滿足攻擊角度和攻擊時間的制導律,并基于預測攔截點設計了剩余飛行時間估計方法。

本文針對導彈以一定落角攻擊裝甲車輛等地面移動目標問題,推導了彈目相對運動模型,在偏置比例導引律的基礎上,結合滑模變結構理論,推導出基于偏置比例導引的落角約束滑模制導律,基于李雅普諾夫穩定性理論設計了參數自適應的冪次趨近律,并結合實際工程應用對趨近律參數進行了進一步設計,減小了導引律在命中點附近的法向過載,進一步提高了導引律的實際工程應用價值,之后,考慮目標機動信息無法準確測量的問題,引入擴張狀態觀測器(extended states observer, ESO),將目標機動造成的彈目視線角速率分量看作擾動量進行觀測,從而對目標速度進行估計,最后對本文提出的制導律的性能進行了仿真分析。

1 彈目相對運動模型

假設目標沿水平面運動,導彈從空中對目標進行打擊,如圖1所示,M為導彈,T為目標,q為彈目視線角,水平基準線沿逆時針方向旋轉到彈幕視線上時為正,θM為導彈的彈道傾角,r為彈目距離,VM為導彈飛行速度,VT為目標運動速度,目標向ox軸正向運動時為正。

圖1 彈目相對運動模型

由圖1可推導出彈目相對運動模型為

(1)

2 基于偏置比例導引的落角約束滑模制導律設計

2.1 滑模面設計

以法向過載ay為控制指令,偏置比例導引律的形式為

(2)

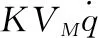
(3)

對式(3)的兩邊從t1到t2進行積分,得

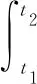
(4)

式中,θM2、q2分別為t2時刻導彈的彈道傾角和彈目視線角；θM1、q1分別為t1時刻導彈的彈道傾角和彈目視線角。將式(4)進行數學變換,得

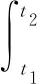
(5)

將當前時刻t和終端時刻tf的各個變量的值代入式(5),得

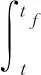
(6)

式中,θMf為命中點處導彈的彈道傾角,通常將落角定義為命中點處導彈的俯仰角,在攻角較小時,俯仰角與彈道傾角近似相等,故本文將θMf作為期望的終端落角;qf為終端彈目視線角。為滿足終端落角約束,在命中點處,希望彈道傾角滿足(θM-θMf)→0,同時,希望彈目視線角滿足(q-qf)→0。當滿足這兩個條件時,有

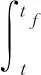
(7)

故將滑模面取為

s=VM(θMf-θM)-KVM(qf-q)

(8)

由式(7)可知,當s趨近于0時,導彈將以期望的彈道傾角θMf擊中目標。

2.2 趨近律設計

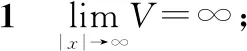
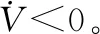
則系統在平衡點x0附近大范圍漸進穩定。將條件2拓展為

(9)

式中,β>0;0<λ<1。對式(9)兩邊從0到系統穩定時刻ts積分,得

(10)

(11)

系統在該平衡點上是全局有限時間收斂的,且收斂時間ts≤V1-λ(0)/(β(1-λ))。

冪次趨近律的基本形式為

(12)

式中,k為趨近速率系數,k>0,

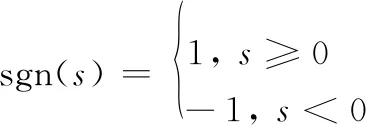
(13)

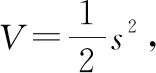
(14)

將式(13)代入式(14),得

(15)

為使系統在有限時間內收斂,將式(9)與式(15)聯立,得

(16)

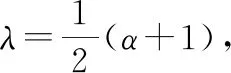
(17)

對于式(11),將ts取為剩余飛行時間tgo, 可以得到

(18)

tgo的估算方法如圖2所示。

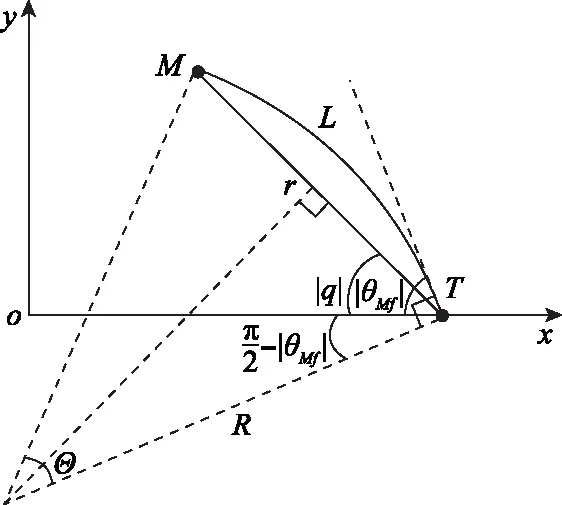
圖2 tgo的估算方法

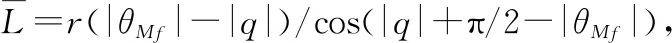
(19)

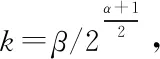
(20)

將式(20)進行數學變換,得

(21)

將式(12)代入式(21),即可得到基于偏置比例導引的落角約束滑模制導律為

(22)

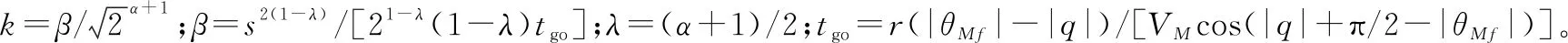
(23)

α是一個可調參數,當α取值較大時,系統會更快地趨近于滑模面,導彈的彈道傾角會更快地趨近于期望落角,在命中點附近的過載指令會更小,但同時最大法向過載指令也會相應地增大;當α取值較小時,系統趨近于滑模面的速度會更慢,同時最大法向過載指令較小,但命中點附近的過載指令會變得較大。

在實際工程應用中,若在命中點附近導彈的法向過載較大,則會導致導彈的攻角較大,容易使導彈在命中目標時發生跳彈,進而影響導彈對目標的毀傷效果[10],故往往希望命中點附近的過載指令趨近于0。同時,為降低導彈設計與制造成本,往往希望導彈的需用過載在滿足導彈戰術技術要求的前提下盡可能小,即希望導彈在飛行過程中的過載指令較小。故本文將α設計為隨時間逐漸變化的時變變量,在初期α取值較小,以減小過載指令,在末期α取值較大,以減小導彈在命中點附近的過載。α的具體變化規律為

(24)

式中,tgo0為根據末制導段初始時刻的彈目信息計算的剩余飛行時間。

3 基于ESO的目標速度估計

本文推導的制導律中需要用到目標速度VT,而在實際工程應用中,往往很難準確地對目標的運動信息進行量測,故需要對目標速度進行估計。本文將目標機動對彈目視線角速率造成的影響看作附加在系統中的擾動,引入擴張狀態觀測器對其進行估計,從而達到對目標速度VT進行估計的目的。

將式(1)的第二式改寫為

(25)

式(25)中等式右邊的第二項與目標速度有關,令[VTsin(-q)]/r=Δf,則有

(26)

設z1=q,z2為擴展的新狀態變量,z2=Δf,設計線性ESO為

(27)

式中，

目標速度的估計值為

(28)

根據文獻[30]所述,ESO中的參數β1、β2可選為

(29)

在實際應用ESO對目標速度進行估計時,隨著導彈接近目標,彈目距離越來越小,由目標機動所引起的擾動會變得越來越大,且由于在命中點附近彈目距離r接近于0,由式(28)計算得到的目標速度估計值與真實值會有較大偏差,故當彈目距離小于一較小值rn時,不再對目標速度進行觀測,認為目標在停止觀測后的時間Δt內的運動速度變化值為小量,并對觀測器的觀測帶寬ωo進行處理,使之隨彈目距離變化而變化,變化規律如下:

(30)

式中,ωo1和ωo2的取值應與實際系統相匹配。本文中取ωo1=10,ωo2=100。

4 仿真分析

為驗證本文所設計的制導律的性能,選取幾種制導律與本文所推導的制導律進行對比仿真分析。

(1) 制導律1(簡稱為BPNG)

文獻[10]提出的基于落角約束的偏置比例導引律:

(2) 制導律2(簡稱為OPNG)

文獻[11]提出的落角約束最優制導律:

為表述方便,將本文推導的制導律簡稱為SM-BPNG。取偏置比例導引系數K=4。在4種場景下對3種制導律進行對比仿真分析。4種場景的仿真初始條件分別如下。

(1) 場景1:導彈飛行速度為270 m/s,初始彈道傾角為0°,期望的終端落角θMf=-60°,導彈的初始位置為(0 m,1 000 m);目標靜止,位置為(3 000 m,0 m)。

(2) 場景2:導彈飛行速度為270 m/s,初始彈道傾角為0°,期望終端落角θMf=-60°。導彈初始位置為(0 m,1 000 m);目標朝x軸正向運動,速度為50 m/s,初始位置為(3 000 m,0 m)。

(3) 場景3:導彈飛行速度為270 m/s,初始彈道傾角為0°,期望的終端落角θMf=-70°。導彈的初始位置為(0 m,1 000 m);目標朝x軸正方向做勻加速運動,加速度大小為3 m/s2,初始速度大小為0 m/s,初始位置為(2 000 m,0 m)。

(4) 場景4:導彈飛行速度為270 m/s,初始彈道傾角為0°,期望的終端落角θMf=-60°。導彈的初始位置為(0 m,1 000 m);目標朝x軸正方向做變加速運動,初始速度為-20 m/s,加速度為[10sin(0.5t)] m/s2,初始位置為(3 000 m,0 m)。

圖3～圖5分別為上述4種場景下,3種導引律的彈道曲線、法向過載曲線和彈目視線角速率曲線。

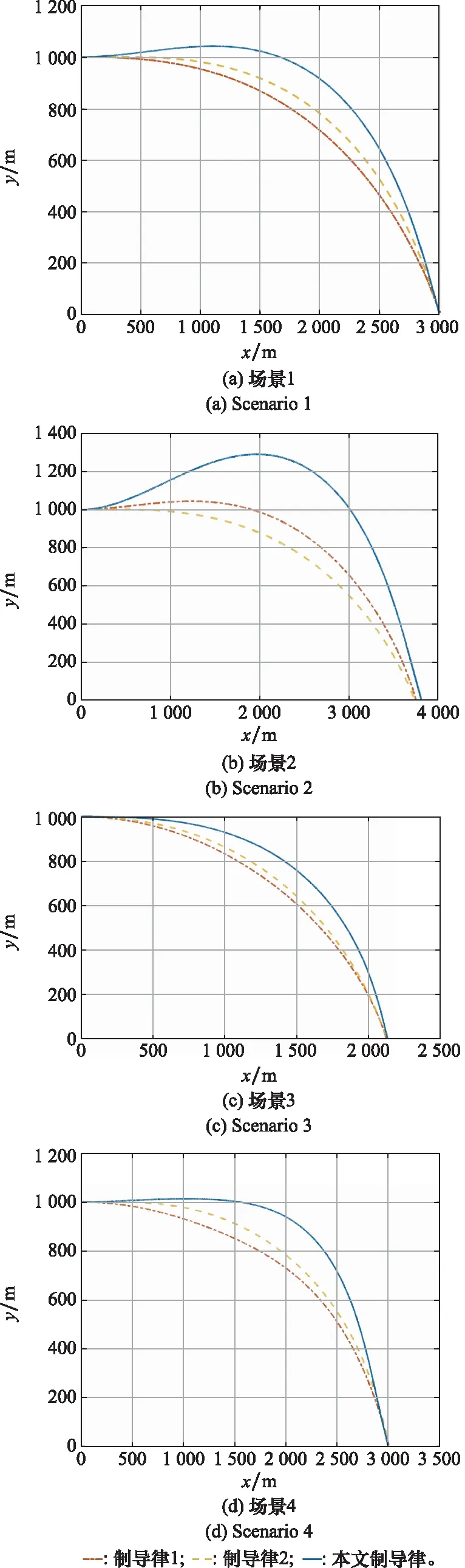
圖3 3種制導律的彈道曲線

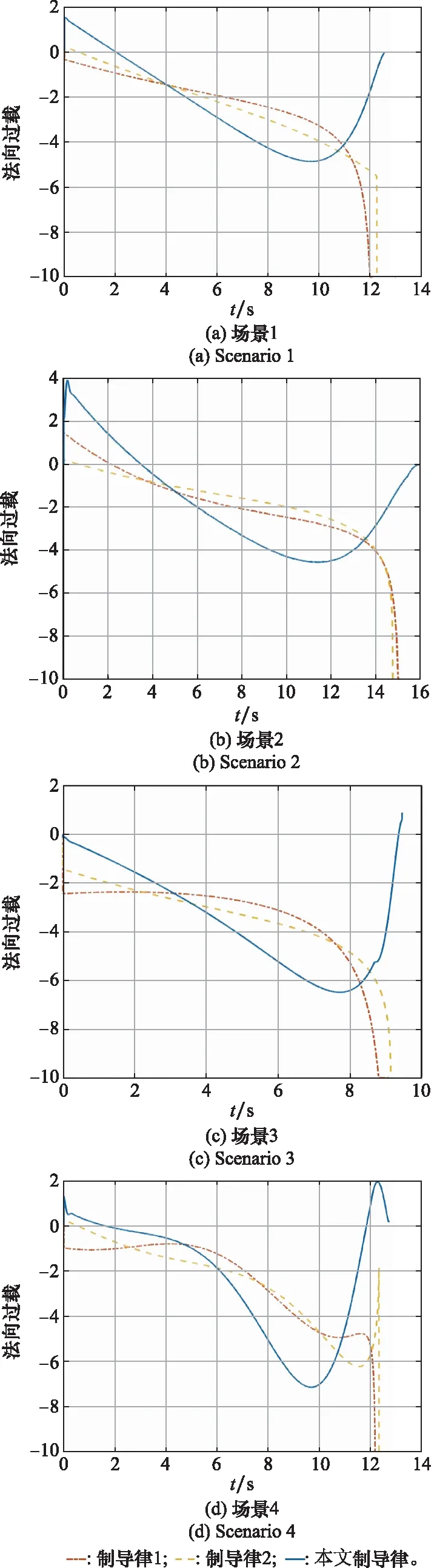
圖4 3種制導律的法向過載曲線

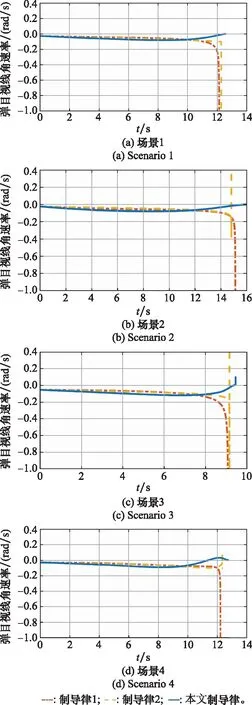
圖5 3種制導律的彈目視線角速率曲線

從圖3中可以看出,在命中點附近,SM-BPNG的彈道比另外兩種制導律的彈道更加平直,同時,SM-BPNG的彈道要更高,飛行距離更長。

從圖4中可以看出,在上述4種場景下,BPNG和OPNG的需用法向過載均較大,SM-BPNG的需用法向過載在3種導引律中是最小的;SM-BPNG在彈道前段的法向過載較其他兩種制導律而言更大,能夠充分發揮導彈的機動能力,而BPNG和OPNG的法向過載在彈道前段較小,在命中點附近均較大,達到了限幅值,較大的法向過載意味著較大的攻角,在實際工程應用中,若導彈的彈道傾角與俯仰角相差較大,則會增加發生跳彈的概率,降低對目標的打擊效果,而SM-BPNG在命中點附近的法向過載較小,在實際工程應用中能夠較好地發揮導彈對目標的毀傷效果。

從圖5中可以看出，4種場景下BPNG的視線角速率均逐漸增大,在命中點附近趨于無窮大;OPNG在命中點附近的彈目視線角速率在場景4中有收斂至0的趨勢,在其他3種場景中均逐漸增大;在4種場景下,SM-BPNG在命中點附近的視線角速率都是3種制導律中最小的。這說明在彈道后段,SM-BPNG的彈道較為平直,能夠使導彈在彈道后段具有較為充裕的機動能力。

圖6為上述4種場景下,SM-BPNG中的ESO對目標速度的估計值與實際目標速度,其中,z1的初值取為初始彈目視線角,z2的初值取0,參數a取0.5,δ取0.05。

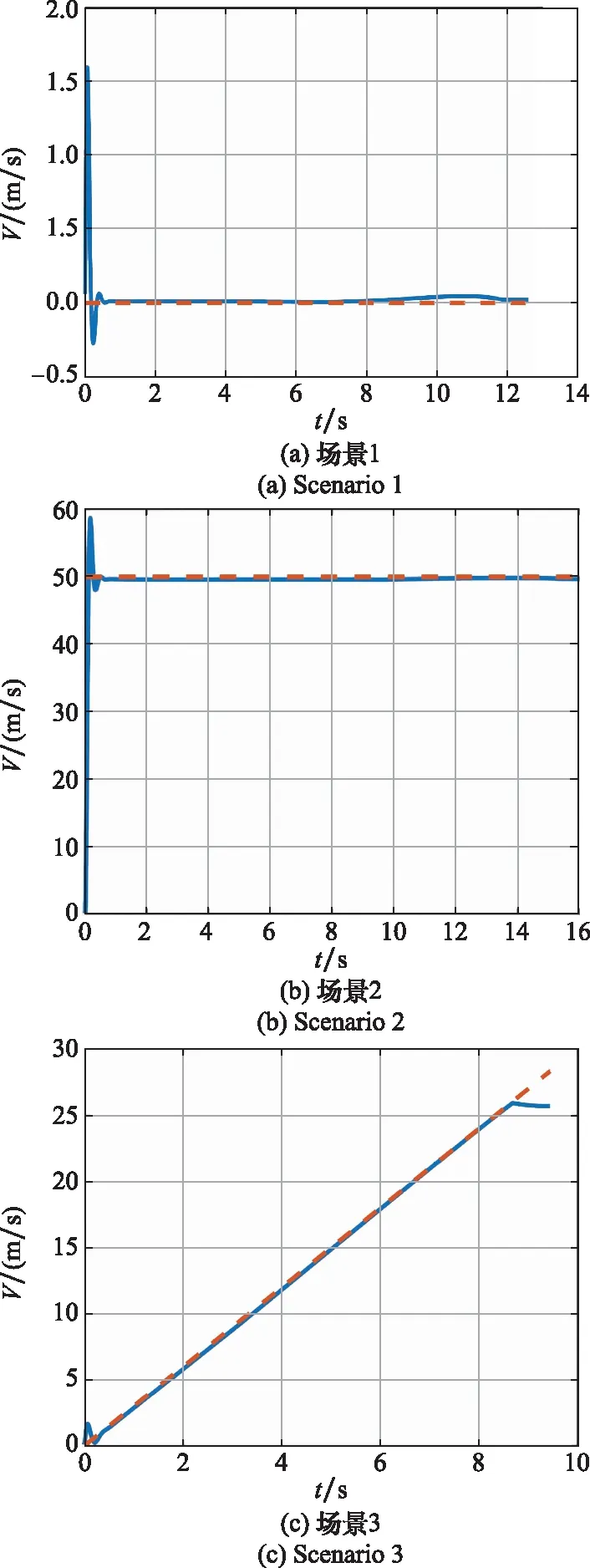
圖6 目標速度的ESO估計值與真實值

從圖6中可以看出,在目標靜止、勻速運動、勻加速運動和變加速運動時,對目標速度的估計值均能夠快速地收斂到目標速度的真實值附近,本文所設計的擴張狀態觀測器能夠對目標速度進行較為準確的估計。

表1與表2列出了4種場景下3種導引律的落角與脫靶量。

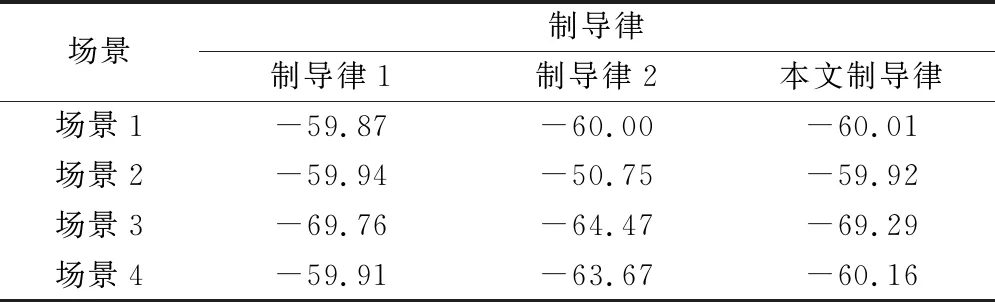
表1 3種制導律的落角

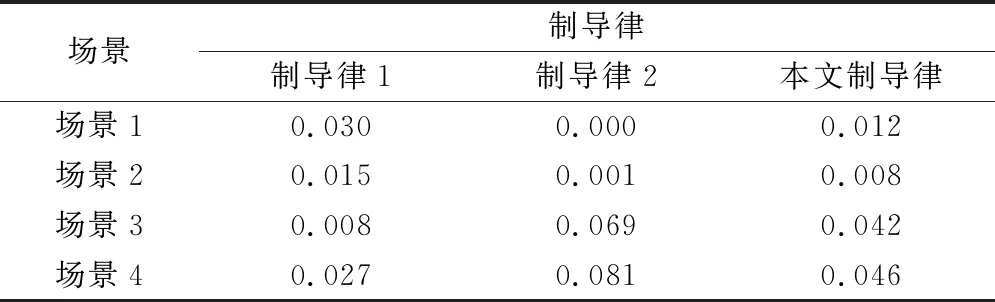
表2 3種制導律的脫靶量

從表1和表2中可以看出,在4種場景下,3種導引律的脫靶量均較小;在目標靜止或做勻加速運動時,3種導引律的終端落角與期望落角的偏差均較小,但當目標進行勻加速運動或變加速運動時,OPNG的終端落角與期望落角的偏差較大,無法較好地滿足落角要求。

相比較而言,BPNG和SM-BPNG的終端落角都能較好地滿足期望落角要求,但BPNG需要準確地測量目標的運動速度,而在實際工程應用中,目標的運動信息往往無法準確知曉,這大大增加了BPNG在實際工程應用中的局限性;SM-BPNG和OPNG都不需要用到目標的速度信息,但OPNG在目標進行勻加速運動和變加速運動時無法較好地滿足落角要求;除此之外,SM-BPNG的需用過載在3種制導律中最小,可以降低導彈的設計和制造難度,并且SM-BPNG在命中點附近的法向過載最小,在實戰中可以較好地發揮導彈的穿甲與毀傷能力。另外,SM-BPNG的彈道前段中較彎曲,能充分發揮導彈的機動能力,彈道后段比較平直,彈目視線角速率較小,能夠使導彈具有較為充裕的機動能力。綜合而言,本文提出的基于偏置比例導引的落角約束滑模制導律能夠在需要用到相對較少的測量信息的同時保證較好的導引性能。

5 結 論

本文針對導彈攻擊裝甲車輛等地面移動目標問題,首先建立了彈目相對運動模型,在偏置比例導引律的基礎上,應用滑模變結構控制理論,推導出了基于偏置比例導引的落角約束滑模制導律。之后,基于李雅普諾夫穩定性理論設計了參數自適應的冪次趨近律,并分析了趨近律中的參數對彈道特性的影響,從實際工程應用的角度出發,對趨近律參數進行了設計。然后,考慮目標信息無法準確測量的問題,引入ESO將目標機動引起的彈目視線角速率分量當做擾動量進行觀測,從而實現對目標運動速度的估計。最后,在4種不同的場景下,將本文提出的制導律與現有的幾種制導律進行了對比分析。仿真結果表明,本文設計的基于偏置比例導引的落角約束滑模制導律能夠以期望的落角和較小的脫靶量打擊靜止目標與機動目標。