可重復使用運載器多約束魯棒預測校正制導
都延麗, 劉 武, 唐明明, 王玉惠
(1. 南京航空航天大學航天學院, 江蘇 南京 211106;2. 南京航空航天大學自動化學院, 江蘇 南京 211106)
0 引 言
可重復使用運載器(reusable launch vehicle, RLV)能夠多次往返于天地之間運輸載荷,在軍事及民用航天領域越來越受到關注,其制導與控制技術代表了未來空天運輸系統的發展方向[1]。然而,RLV再入過程中存在諸多復雜約束,如制導終端約束,熱流密度、動壓、過載等過程約束,禁飛區、航路點等地理約束,傾側角約束,同時還須考慮再入參數不確定性,這些問題對RLV的再入制導系統設計提出了嚴峻的挑戰。
針對過程約束等常規約束,通常采用預先設置約束走廊對阻力加速度或傾側角進行限制的方式[2-4],以使飛行器不突破再入約束,保證再入過程的安全性。例如文獻[2]將過程約束轉化為阻力-能量走廊,通過設計標稱阻力加速度剖面,并利用其二階導數得到傾側角幅值。Lu[3]提出統一適用的再入預測校正制導方法,較好解決了軌跡高度震蕩和過程約束問題。標稱軌跡與優化算法的結合也被用來解決此類問題,如凸優化算法[5-6]等方法被應用于再入軌跡的在線規劃與跟蹤,但是優化算法的引入同時也增加了系統調參的復雜性。
對于地理約束問題,如航路點、禁飛區等,快速生成滿足該約束的再入軌跡并對其進行跟蹤是研究思路之一[7-9]。高斯偽譜法[10-11]作為再入制導的熱門方法被廣泛研究,其與預測校正法結合的混合制導也成為解決此類問題的一種思路[12]。人工勢場法[13-14]、虛擬觸角探測[15-16]等機器人避障領域的算法被應用于再入制導實現禁飛區的規避。Wang等[17]將禁飛區和航路點轉化為一系列參考點,采用模糊邏輯在參考點間尋找合適的傾側角翻轉位置。文獻[18]通過定義航路點的航跡方位角可達域和控制集,給出滿足航路點約束的傾側角翻轉策略,并進一步將其應用于末端方位角約束[19]。雖然上述方法在解決地理約束問題上較為有效,但是再入環境復雜多變,當存在一定程度的參數不確定時,飛行器的機動能力會受到很大影響,可能無法滿足地理約束,甚至影響再入任務的完成。
關于參數不確定性的魯棒制導問題,基于標稱軌跡的跟蹤優化方法多采用神經網絡[20]、干擾觀測器[21-22]等方法來在線估計不確定性。而預測校正制導方法對初始誤差不敏感以及較高的制導精度等優越性令其在魯棒制導研究領域具有廣闊前景。根據測量到的升阻力對氣動參數進行修正是增強系統魯棒性的一種方法[3,23-24]。文獻[25]通過漸消記憶最小二乘法建立環境參數預測模型,對其進行在線估計和修正,基于在線環境參數模型進行落點預測,以克服擾動對制導精度的影響,增強了系統的魯棒性。但是,盡管在可以修正氣動參數的情況下,飛行器實際升阻比的改變仍導致其縱程和橫程能力都受到影響,因此還需要進一步對制導指令進行調整。
同時,考慮控制系統的執行能力,有必要對傾側角的翻轉速率進行約束,但一般方法僅對制導系統輸出的傾側角幅值指令施加限制[4],并未將速率約束轉化到預測校正過程之中。另外,從制導的驗證模型來看,大多數文獻采用體積小、質量輕、側向機動能力強的CAV-H模型[7],但是RLV作為運載工具,其體積和質量較大,側向機動能力偏弱,橫向制導難度較大,因此有必要針對中大型RLV模型來驗證復雜多約束條件下的再入魯棒制導算法的有效性。
基于以上分析,本文選擇具備完整橫側向氣動參數數據的HORUS-2B[26]作為驗證模型。以預測校正制導方法為基礎,利用改進準平衡滑翔條件將常規約束轉化為傾側角幅值約束,并進行了如下創新工作。
(1) 提出了一種基于二分法快速迭代搜索滿足航路點約束的傾側角翻轉策略,在此過程中將傾側角最大翻轉速率約束轉化為關于能量變化的速率約束,參與預測校正的計算過程;
(2) 為了進一步增強制導系統的魯棒性,在考慮再入參數不確定的情況下,提出了基于標稱升阻比和剩余能量剖面自適應調整迎角和橫程誤差走廊的魯棒制導策略;
(3) 通過充分的仿真驗證了所提出方法在中大型RLV模型上的可行性和實用性。
1 問題描述
考慮地球自轉的影響,建立RLV的三自由度無量綱化制導方程[3]如下:
(1)
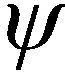
(2)
式中,ρ表示大氣密度;Sref是機翼表面積;m為飛行器質量;g0=9.8 m/s2是地球重力加速度;CL和CD分別代表升力系數和阻力系數,其值與迎角α(再入制導的另一控制量)和馬赫數相關。
在此基礎上,參考文獻[3]引入能量變量e(e=1/R-V2/2),e對無量綱時間τ的導數為
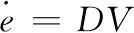
(3)
同時引入待飛航程s關于能量的導數:
(4)
式中,s表示飛行器當前星下點位置(θ,φ)到目標點星下點位置(θf,φf)之間的大圓弧長度。進一步將式(1)轉化成關于能量e的無量綱方程[3]為
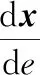
(5)
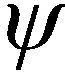
2 再入約束及其轉化
2.1 過程約束及其轉化
再入過程中RLV主要受到熱流密度、過載、動壓的過程約束以及平衡滑翔條件的限制。過程約束[3]具體形式如下:
(6)
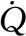
常規的平衡滑翔條件對于再入問題來說要求過于嚴苛,有可能造成RLV熱流約束段軌跡有比較嚴重的震蕩。為抑制震蕩,采用改進的平衡滑翔條件[27](modified quasi-equilibrium glide condition, MQEGC),具體形式為
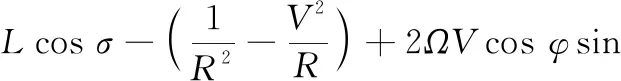
(7)
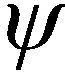
(8)
式中,Rcrd=R0+hcrd;hcrd和Lcrd分別為當前速度V對應的再入走廊下邊界高度和升力加速度。
2.2 航路點約束、終端約束和傾側角速率約束
航路點約束可以描述為再入過程中RLV需要通過的某些特定的經緯度點,以進行載荷釋放、對地監測、技術驗證等特殊任務,即
φ=φ1|θ=θ1
(9)
式中,(θ1,φ1) 代表預先設置的航路點經緯度。
終端約束包括高度、速度與末端目標點經緯度約束,其中前兩者可以轉化成末端能量約束。終端約束以及傾側角速率約束的表達式如下:
(10)
(11)
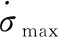
3 初始下降段制導
初始下降段的高度較高,空氣稀薄,無法滿足平衡滑翔條件,一般采用常值傾側角飛行,不對制導系統進行指令校正。同時在此階段,為使RLV快速通過熱流密度段,通常以大迎角再入,從而使飛行器高度快速下降,減小總吸熱量,為熱防護系統減小壓力。該段制導過程中會一直判斷RLV是否滿足平衡滑翔條件,滿足此切換條件后,立刻切換至滑翔段制導,即
(12)
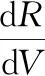
4 滑翔段多約束魯棒制導
4.1 航路點約束的任務評估
由于航路點是預先設定的任務點,而飛行環境復雜多變,對于飛行器是否有足夠的側向機動能力完成此任務,應該給出一種簡便可行的在線評估方法,因此本文將航路點任務轉化為判斷不等式是否成立的問題。假設存在航路點任務(θ1,φ1),當前狀態點經緯度為(θ0,φ0),那么,飛行器在θ0到θ1中間某處θr傾側角發生一次翻轉后到達經度θ1處的緯度可以表示為關于翻轉位置θr的函數φ(θr)。在不同的θr處發生翻轉后,到達θ1處的緯度φ(θr)不同。通過對式(5)進行積分可以預測在不同翻轉位置θr處發生翻轉后RLV到達航路點處的緯度φ(θr),則航路點任務預測得到的緯度誤差可以表示為
E(θr)=φ(θr)-φ1
(13)
在飛行器的側向機動能力能夠滿足航路點任務需求的情況下,必然滿足:
E(θr=θ0)E(θr=θ1)<0
(14)
如果此不等式成立,那么必定存在一個位于θ0到θ1之間的θr,使得在θr處發生傾側角翻轉時,E(θr)=0,具體分析如圖1所示。
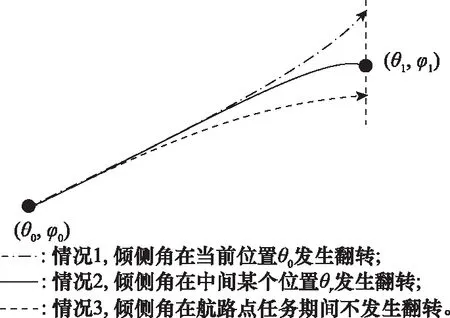
圖1 不同翻轉位置對航路點任務的影響
4.2 航路點側向制導
航路點側向制導的任務首先是確定傾側角的翻轉位置,在保證末端航向角或橫程誤差滿足要求的同時準確通過預先設定的航路點。基于第4.1節的評估方法,可以將航路點約束轉化成尋根問題。本文通過改進快速二分法迭代尋找滿足要求的θr,即假設傾側角在θ0到θ1中間的θr處翻轉,那么以此側向邏輯進行制導,當飛行器到達航路點,將使緯度誤差滿足
|E(θr)|≤μ
(15)
式中,μ為允許誤差常數,此式即為二分法迭代終止條件,滿足此條件的θr即為所求翻轉點。
進一步給出迭代流程如下。
步驟 1首次確定航路點任務的傾側角翻轉位置θr,二分法迭代初始點選為當前點經度θ0和航路點經度θ1,迭代求得滿足精度要求的θr。
步驟 2當需要再次校正傾側角翻轉位置時,不再直接以當前狀態點作為二分法的初始點進行迭代,而是首先計算3個翻轉位置θ0,θ1和θr到達航路點的緯度誤差E(θ0),E(θ1)和E(θr),通過選擇與E(θr)符號相反的另一個翻轉點作為二分法的起始點,重新校正θr,由此可以大大減小迭代積分次數,加快系統指令的解算。
步驟 3通過判斷飛行器實時經度是否到達步驟2迭代得到的翻轉點θr,若到達,則進行一次傾側角翻轉,并在保證到達航路點之前,傾側角符號不變,若未到達,則繼續重復步驟2。
步驟 4判斷航路點任務是否全部完成,若已完成,則進行常規末端制導,若未完成,則轉向步驟1。
航路點側向制導的下一步是確定傾側角的符號。以再入過程的經度θ單調遞增為例,在上述迭代過程下,給出傾側角符號的確定策略為
(16)
式中,sgnz(σ)為開始執行航路點任務時的傾側角符號;f(Z)表示橫程誤差走廊Z的策略函數。
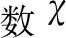
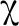
(17)
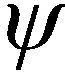
s=arccos(sinφsinφf+cosφcosφfcos(θf-θ))
(18)
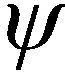
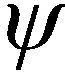
(19)
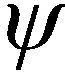
(20)
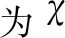
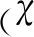
(21)
然后,對于Z采用收斂的橫程誤差走廊:
Z=k1s
(22)
式中,k1為橫程誤差走廊的斜率。進一步,如果簡單判斷每一時刻的橫程超過走廊邊界就立刻進行傾側角符號翻轉,則會發生如圖2所示的錯誤情況,橫程在上一次傾側角翻轉后正在向走廊內偏轉時,又進行傾側角符號判斷,導致其符號發生混亂。
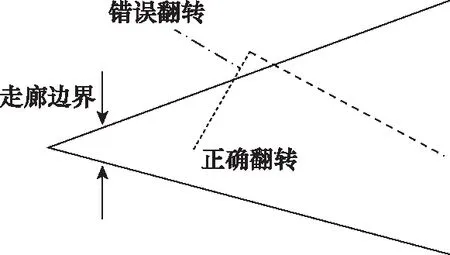
圖2 傾側角錯誤翻轉示意圖
針對此情況,本文給出翻轉邏輯:

(23)
式中,pre_sgn(σ)表示前一時刻的傾側角符號。由于在執行航路點任務期間不依靠橫程誤差走廊對橫程進行約束,因此一般執行完航路點任務后飛行器的橫程是超過走廊邊界的,采用此翻轉邏輯同樣可以保證后續傾側角符號不發生紊亂。
4.3 縱向制導
側向制導已經確定了傾側角的翻轉位置和符號,縱向制導的任務則是確定并不斷積分校正傾側角的幅值。以末端待飛航程的偏差為校正準則,當再入能量e=ef時,記末端待飛航程為
f(σ)=s(ef)
(24)
只要在每一個制導周期內給定傾側角初值σi,就可以不斷對式(5)積分,積分步長為Δe,并采用割線法進行迭代,快速尋找滿足精度要求的傾側角幅值,具體迭代策略為
(25)
由于常規的線性傾側角模型在制導周期較長時會出現傾側角指令不連續的情況,導致控制系統的壓力變大,進而影響制導精度,因此本文的傾側角幅值模型采用文獻[27]提出的二次函數模型,并使其滿足式(8),可得
(26)
通過迭代尋找滿足末端待飛航程精度要求的c值,則a,b的值可以由下式得到:
(27)
式中,e0和σ0為當前狀態的能量和傾側角;σf為末端傾側角值,取值在60°~70°。在積分過程中,若航路點任務的傾側角還未翻轉,則傾側角的符號由航路點任務的側向制導方法確定,反之,則由式(22)的橫程誤差走廊確定。本文設計的考慮航路點約束在內的再入預測校正制導確定傾側角的整體流程圖如圖3所示。
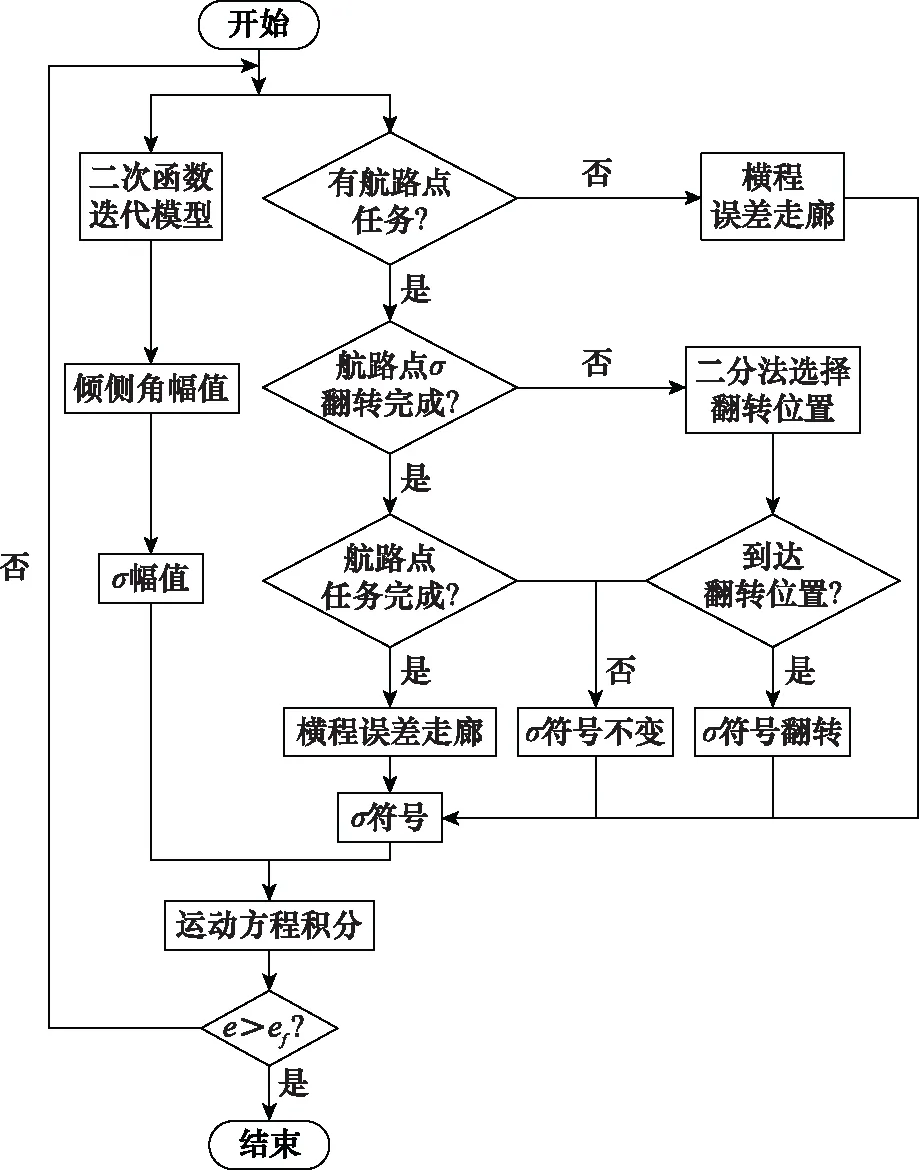
圖3 航路點制導確定傾側角流程圖
4.4 傾側角速率約束轉化
在實際應用中,由于控制系統的執行能力有限,不能立刻在迭代得到的傾側角翻轉點進行翻轉,即翻轉速率有一定約束限制,如式(11)所示。此約束對航路點任務的執行精度有一定影響,而且速率限制越小,導致航路點任務的精度越差。但是若不限制翻轉速率,實際姿態控制系統將很難準確跟蹤制導指令。因此,本文對該約束進行了一定處理,引入到預測校正制導律當中。
預測校正制導算法通常對關于能量e的方程進行積分,故需要對式(11)進行轉化。假設無量綱時間τ對時間t的轉換關系為
(28)
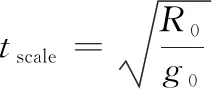
根據式(3)和式(28)可將式(11)變換為
(29)
當需要做σ翻轉機動時,其值可由式(30)確定,表示為
(30)
式中,σpre表示前一時刻的傾側角幅值;σ(e)是用于預測校正過程中傾側角翻轉機動的數值;Δe代表預測校正的積分步長;σ(t)是實際過程中的傾側角翻轉機動值;Δt為實際的積分步長;sgn(σcmd)表示翻轉機動的目標傾側角符號。
通過以上轉化,此約束可以直接應用于預測校正的過程當中。在進行步驟1~步驟4迭代時,直接考慮帶有傾側角關于能量變化的速率約束后,能夠使迭代得到的翻轉點更加準確,進一步提高了制導精度。另外,此轉化方法不限于航路點制導,同樣適用于常規預測校正制導。
4.5 再入魯棒制導
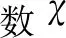
(31)
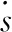
(32)
(33)
式中,k1為走廊的斜率常數;(L/D)和(L/D)c代表實際升阻比和標稱升阻比。根據不同升阻比差異調整橫程誤差走廊的寬度,從而保證傾側角不會過多(或過少)地翻轉,提高末端制導精度。
當升阻比減小時,飛行器的橫程和縱程能力都會下降。那么在執行航路點任務時,根據上文提出的任務評估方法,可能在當前經度點θ0到航路點經度θ1之間并不存在滿足航路點精度要求的翻轉點θr,即式(14)不成立,則會直接導致航路點甚至再入任務的失敗。通常,再入迎角的變化對升阻比有影響。本文根據HORUS-2B的氣動參數模型給出了不同馬赫數(Mach)下升阻力系數之比隨迎角的變化關系如圖4所示。
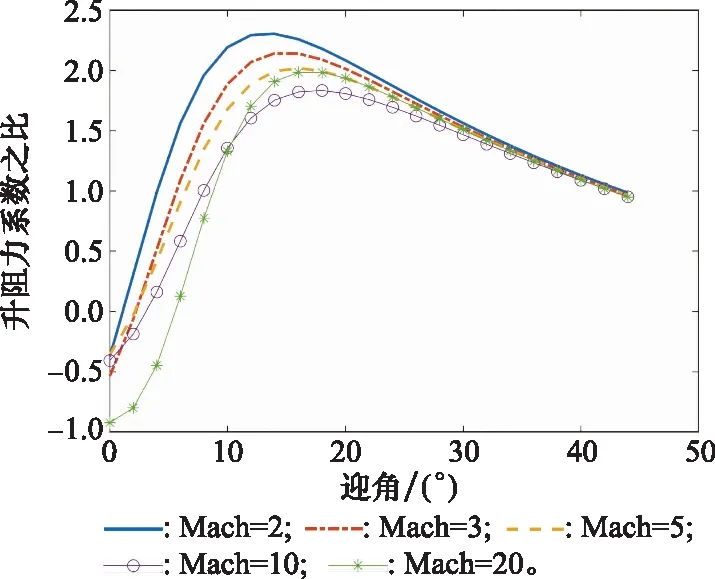
圖4 升阻比隨迎角的變化情況
從圖4可以看出,升阻比隨著迎角的減小先增大后減小,其臨界點為最大升阻比迎角。為增強航路點制導系統的魯棒性能,考慮自適應調整迎角剖面。本文首先參考文獻[29]設計了基于能量的標稱迎角剖面,由于再入過程中馬赫數和剩余能量均為單調遞減的變量,故為了描述標稱迎角剖面和最大升阻比迎角的關系,將其轉換在馬赫數-迎角坐標系下進行對比,如圖5所示。
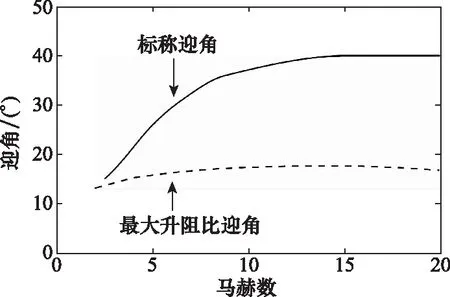
圖5 迎角剖面情況
如果直接依據升阻比差值,當升阻比小于標稱升阻比時減小迎角,那么再入后期當標稱剖面與最大升阻比迎角邊界比較接近時,一旦調整后的迎角值小于最大升阻比迎角,則可能導致飛行器的升阻比快速降低,飛行器橫程和縱程飛行能力急劇下降,反而因減小迎角造成相反的效果。
進一步地,單獨以升阻比差值作為調整基準,會造成飛行器迎角的調整值過于固定,末端制導精度不高。因此,本文在此基礎上引入剩余能量Se,由于能量在再入過程中為一個單調遞增的量,故Se的具體形式如下:
Se=ef-e
(34)
式中,ef代表末端能量。
整個再入過程實際為一個能量耗散的過程,當迎角大于當前馬赫數下最大升阻比迎角時,迎角越大,能量耗散越快,反之,能量耗散越慢。而一旦迎角小于最大升阻比迎角,則能量耗散速率的變化與上述邏輯相反。當升力減小,阻力增大時,飛行器會因為剩余能量不足,不能完成航路點任務;升力增大,阻力減小,飛行器剩余能量過多,飛行器的橫程和縱程能力均增強,若不對其進行處理,則會導致飛行器飛過末端點,使得落點精度變差。基于以上分析,為了減小控制系統的壓力,僅在飛行器升阻比減小(即橫程縱程能力變差)的情況下對標稱迎角進行調整,而對升阻比增大的情況,通過式(33)增大橫程誤差走廊斜率就可以消耗掉多余的能量。
根據標稱升阻比和剩余能量剖面,本文提出如下迎角調整策略:
(35)
式中,Δα為迎角調整量;k2和k3是調整增益;(L/D)c和Sec為標稱情況下的升阻比和剩余能量剖面。須注意的是,當調整量使調整后的迎角小于圖4的最大升阻比迎角邊界時,則以最大升阻比迎角飛行,不再繼續減小迎角,即實際α為
(36)
式中,αc表示預先設計的標稱迎角剖面;amax(L/D)表示最大升阻比迎角。
總體來看,第4部分設計了針對航路點約束的改進預測校正制導算法,同時將傾側角翻轉速率約束轉化為關于能量的約束,并提出自適應調整迎角及橫程誤差走廊的方法以增強了預測校正制導方法的魯棒性能。
5 仿真結果與分析
本文以HORUS-2B飛行器為研究對象[26],其初始和終端狀態的設置如表1所示。

表1 初始狀態和終端狀態約束
5.1 傾側角翻轉速率約束下的航路點制導仿真
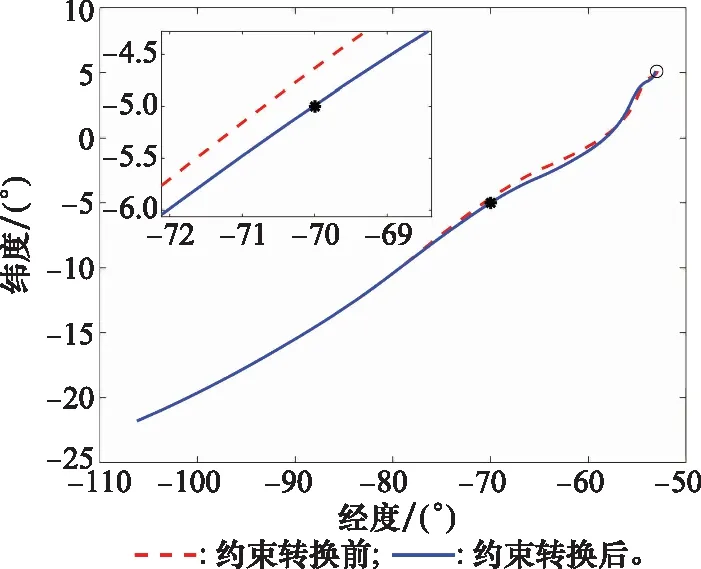
圖6 傾側角翻轉速率約束下的軌跡對比
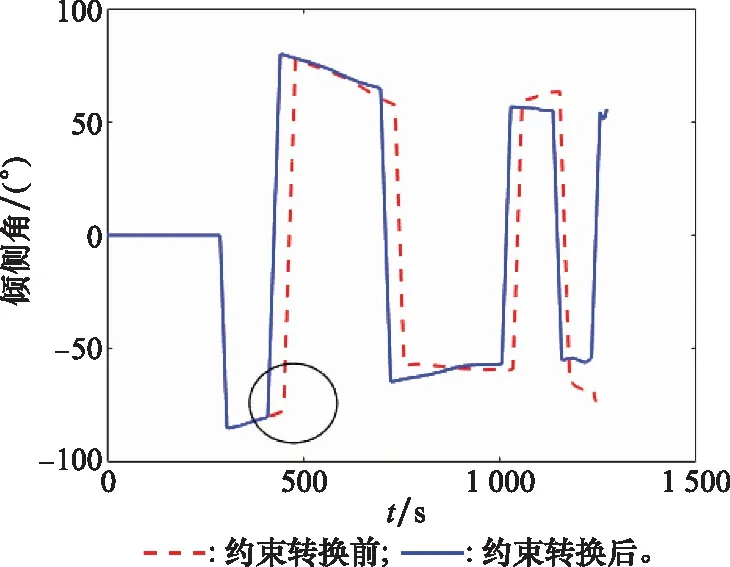
圖7 傾側角翻轉速率約束下的傾側角對比
從圖6可以看出,傾側角翻轉速率約束對航路點的精度有一定影響。由于實際情況下傾側角不能立即翻轉,因此理論計算得到的傾側角翻轉位置在實際情況中已經滯后,通過應用本文提出的約束轉化方法,可以在預測過程中考慮傾側角翻轉速率,將理論計算的翻轉位置提前,如圖7中圓圈所示。提出的方法依然保證了很好的航路點任務精度,同時也為后續控制系統的指令跟蹤減小了負擔,具有一定的工程實用性。
5.2 標稱情況下的航路點魯棒制導仿真
對兩種極限情況下(情況1:CD+15%,CL-15%;情況2:CD-15%,CL+15%)的航路點任務進行仿真。方法1采用文獻[3]中的預測校正方法,僅將其傾側角符號確定邏輯更換為式(22)的橫程走廊。由于提出的傾側角翻轉速率約束轉化方法已在第5.1節驗證過其有效性,因此為了單純驗證本文所提出方法的魯棒性,對文獻[3]的方法進行了改進,將傾側角翻轉速率約束的轉化方法也應用于方法1。方法2即本文提出的方法。首先在飛行器橫程和縱程能力最差的情況(情況1)下,對兩種方法的航路點任務完成與標稱情況作對比結果如圖8和圖9所示。從圖8中可以看出,當升阻比減小導致飛行器縱程和橫程能力下降時,在方法1作用下,飛行器雖然能夠完成航路點1的任務,但是剩余能量已經不足以完成接下來的航路點2和末端制導任務。通過本文的調節方法,在方法2下飛行器能夠較為精確地完成兩個航路點任務和最后的末端制導任務。
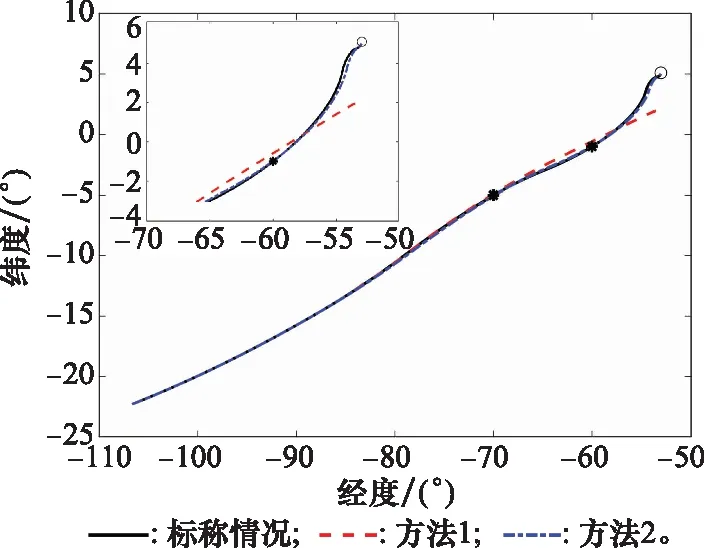
圖8 再入軌跡對比情況(情況1)

圖9 剩余能量對比情況(情況1)
通過本文的方法調整,從圖9(情況1)可以看出剩余能量足夠完成再入制導任務,并且在末端點趨近于0,滿足再入任務的要求。只要飛行器橫程和縱程的最短極限情況下能夠有足夠的剩余能量完成再入任務,那么其余情況下不會出現剩余能量不足的情況。
在情況2下,相應對應結果如圖10和圖11所示。
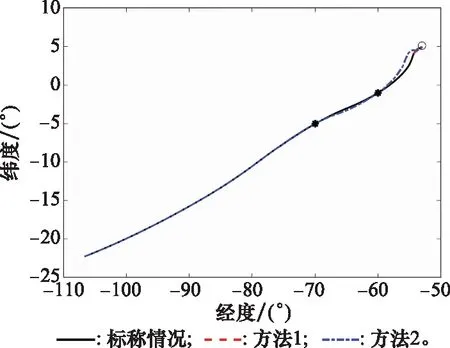
圖10 再入軌跡對比情況(情況2)
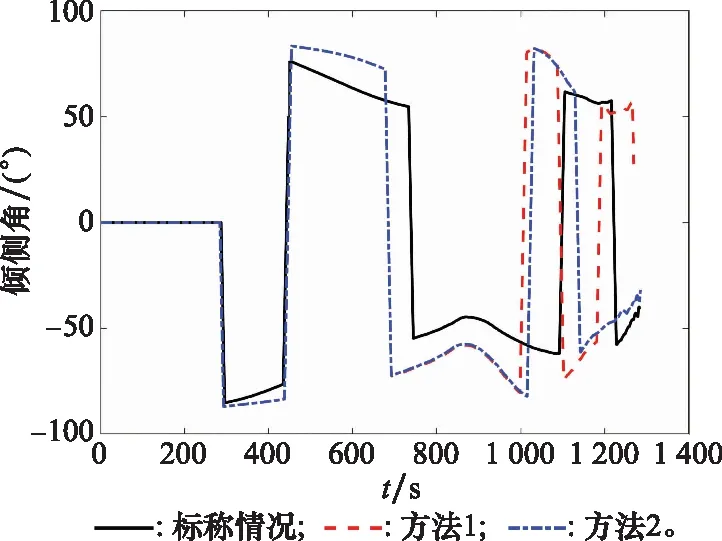
圖11 傾側角對比情況(情況2)
從圖10所示的再入軌跡情況來看,在情況2下,兩種方法的飛行器都能夠完成再入任務。當升阻比變大時,飛行器的升力增大,橫程變化率加快,飛行器的剩余能量變多。如果依然采用標稱的橫程誤差走廊,雖然航路點任務能夠較好完成,但是飛行器必然需要通過更多的傾側角翻轉去消耗剩余的能量(方法1),而通過增大誤差走廊的斜率,可以在航路點任務完成的末端制導階段,通過增加橫程的方式消耗能量,從而減少傾側角翻轉,減小控制系統的壓力。如圖11所示,在本文的調整方法下(方法2),末端傾側角的翻轉次數相比于未調整之前減少一次,但是并不影響整個制導過程的精度。
5.3 擾動情況下的蒙特卡羅仿真
為了充分模擬再入過程的隨機干擾和不確定性,本文在標稱情況下對一些不確定量施加符合高斯分布(3σ)的隨機干擾,如表2所示。
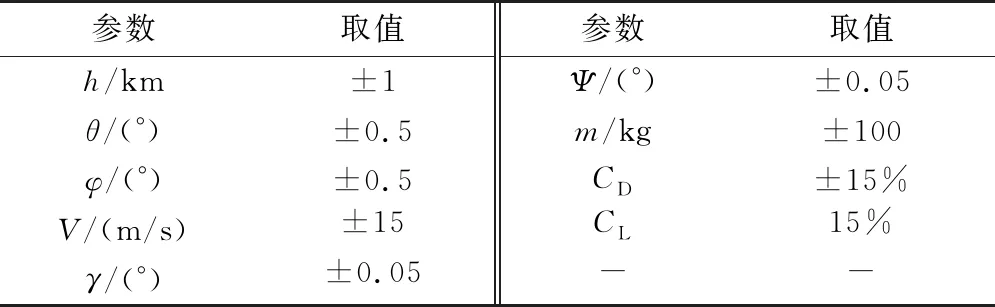
表2 蒙特卡羅仿真的高斯擾動
由于大氣密度是高度的函數,故式(6)能夠轉化成速度與高度相減(h=R-R0)的函數,根據此函數可確定RLV在V-h空間內的再入走廊下邊界,如圖12所示。
大氣密度模型采用US-76標準大氣模型,擾動模型采用文獻[30]提出的大氣密度擾動模型。在此條件下對本文制導算法進行了300次的蒙特卡羅仿真實驗,具體結果如圖12~圖16所示。圖12和圖13給出了再入過程的高度-速度以及經緯度軌跡。從圖上可以看出,在多種擾動條件下,飛行器能夠精確完成兩個航路點任務,到達預定末端目標區域,并滿足預先設置的再入走廊約束。圖14進一步給出兩個航路點的緯度誤差分布,其誤差不超過±0.1°。
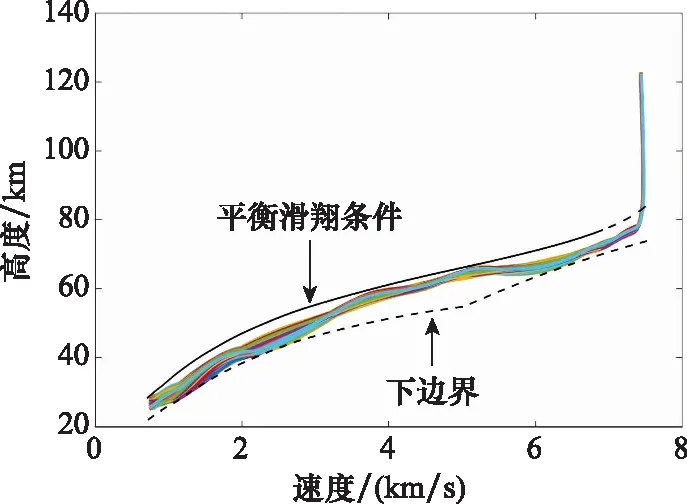
圖12 速度-高度剖面情況
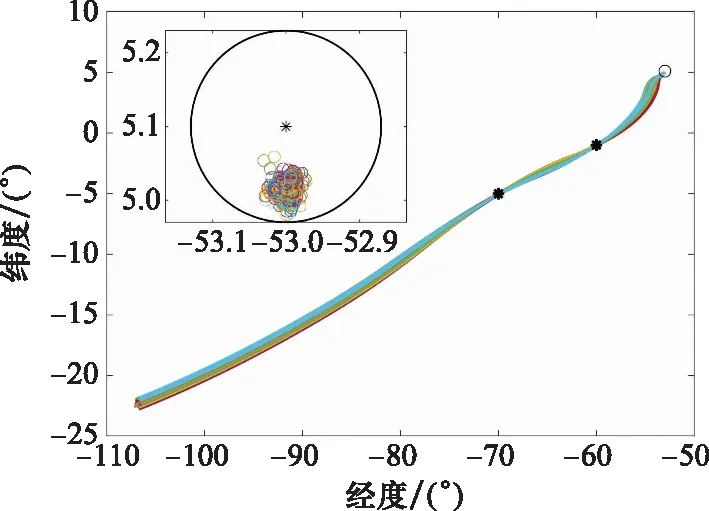
圖13 軌跡情況
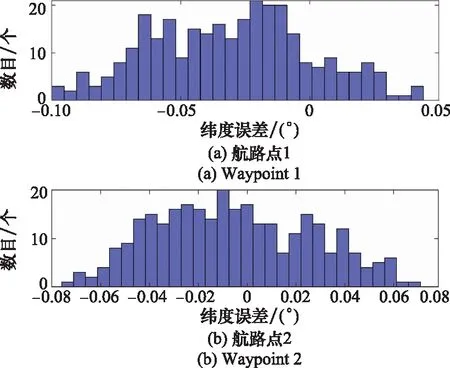
圖14 航路點誤差分布情況
從圖15來看,再入過程約束也未突破,保證了制導的安全性。圖16的大多數傾側角翻轉次數為5次,其中第1次為初始下降段與平衡滑翔段切換的傾側角翻轉,第2次和第3次分別為執行航路點任務的傾側角翻轉,在末端制導過程中,傾側角翻轉次數基本控制在2次以內,并且不影響落點精度。綜上所述,本文提出的方法對再入過程中的不確定性具有較好的魯棒性。
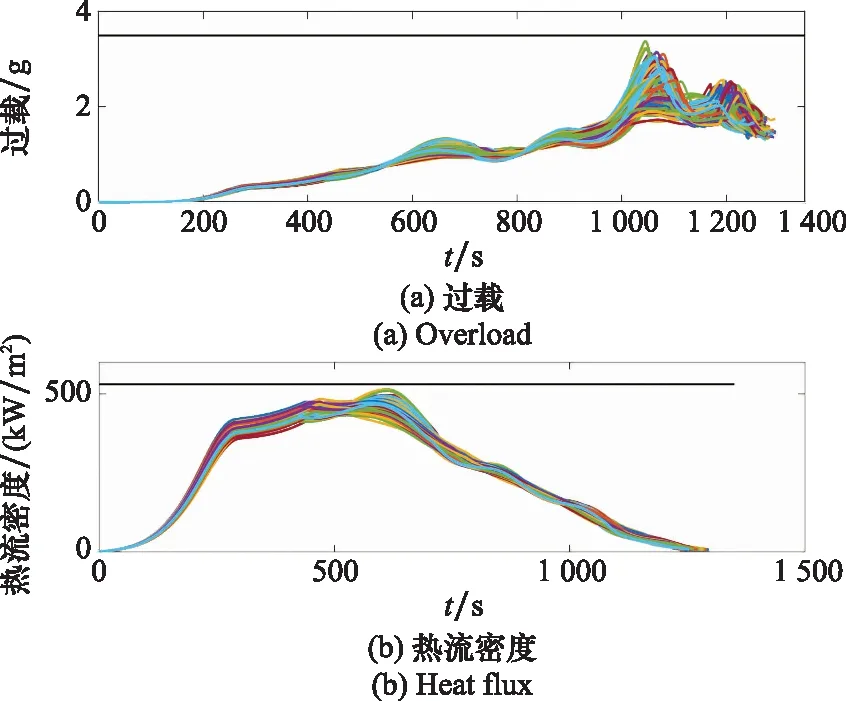
圖15 約束變化情況
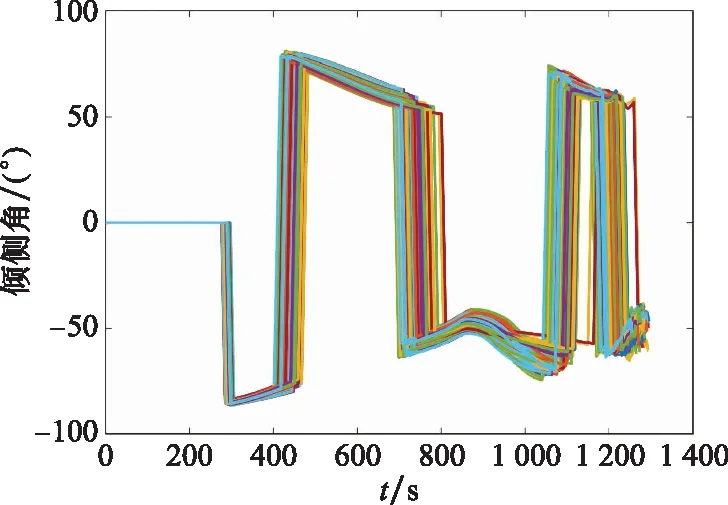
圖16 傾側角
6 結 論
本文針對RLV再入過程中存在參數不確定的航路點飛行任務,提出了一種多約束魯棒預測校正制導方法,主要的結論如下:
(1) 針對航路點約束,提出一種航路點任務評估方法,能夠將任務轉化為不等式問題,通過判斷不等式是否成立來對航路點任務進行評估;
(2) 基于評估方法,將航路點約束轉化成尋根問題,通過改進二分法快速迭代尋找滿足要求的傾側角翻轉位置,并將傾側角翻轉速率約束轉化為關于能量的速率約束,在預測校正過程中進行計算,有效提高了航路點任務的精度;
(3) 考慮再入參數的不確定性問題,提出一種根據標稱升阻比和剩余能量對迎角和橫程誤差走廊進行在線調整的方案,增強了多約束預測校正制導系統的魯棒性能;
(4) 對提出的方法進行了充分的蒙特卡羅仿真實驗,驗證了方法的有效性和魯棒性。

