對稱分布的矩刻畫

廖俊俊， 劉繼成， 吳 娟

(華中科技大學 數學與統計學院， 武漢430074)

1 引 言

定義設隨機變量X的概率密度為f(x)，若存在某點c，使得對任意的x有f(c+x)=f(c-x)， 則稱X的分布關于c對稱.

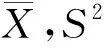
證記E(X)=μ，D(X)=σ2.

必要性 由β=0， 有

μ3=E[X-E(X)]3=Cov(X，X2)-2E(X)D(X)=0，

即

E(X3)-μ3-3μσ2=0，

μ3=E[X-E(X)]3=E(X3)-μ3-3μσ2=0，β=0.

例1說明對稱分布的偏度(若存在)是0. 然而，隨機變量的偏度只能度量分布的偏斜方向和程度，描述概率密度在左右尾部的相對拉長趨勢. 偏度為0，并不足以推出概率分布是對稱的. 下面的兩個例子說明存在偏度為0的非對稱分布.

例2設隨機變量X的概率密度函數為

X的偏度β為0，且X的分布非對稱.

證易知E(X)=E(X3)=0，所以X的偏度是0. 由f(-x)≠f(x)知X的分布非對稱.

通過隨機抽樣方法得到樣本的偏度為0，而總體的分布可能是對稱的，也可能是非對稱的.

例3設總體X服從混合高斯分布，概率密度函數為

f(x)=ωf1(x)+(1-ω)f2(x)，

(ii) 令ω=0.9，μ1=-μ2=-3，σ1=20，σ2=0.1，產生隨機數10000個，計算得到樣本的偏度接近于0，由圖1右圖可以看到，X的分布是非對稱的. 因此，僅憑偏度并不能判定概率分布是否對稱.

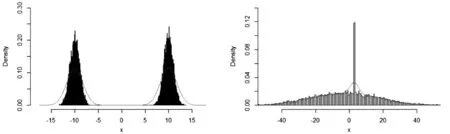
ω=0.9，μ1=-μ2=-3， σ1=20，σ2=0.1圖1 混合高斯分布的樣本

既然偏度不足以保證分布的對稱性，那么給出一個分布關于0對稱的判別是必要的. 本文嘗試基于傅里葉變換的思想，從矩的角度討論對稱分布的充要條件.

2 主要結論

顯然，隨機變量X的分布關于c對稱等價于X-c的分布關于0對稱. 因此，只需討論概率密度f(x)關于0對稱的情形，即f(x)是偶函數. 李賢平[1]證明了隨機變量的分布關于0對稱的充要條件是特征函數是實的偶函數. 下面定理從隨機變量原點矩的角度給出X的分布關于0對稱的充要條件.

定理設隨機變量X的概率密度函數f(x)在上連續，對任意正整數k，積分x2k+1f(x)dx絕對收斂，且f(x)在[-a，a]之外取零，則X的分布關于0對稱的充要條件是

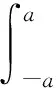
證必要性顯然成立. 下證充分性.

由題設，?M>0，使得|f(x)|≤M，?x∈(-∞，+∞)，且f∈L1(-∞，+∞). 知道

易知有估計

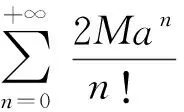
若不要求f(x)有界，則上述定理是X的分布關于0對稱的充分條件. Shiryaev[3]給出隨機變量X的特征函數φ(t)能展成冪級數的必要條件是：若對任意的n≥1，有E|X|n<∞，且

則

但是結論中t的取值范圍是有限區間.

例2(續)雖然X的偏度是0. 但是，E(X5)=64/14553≠0. 由定理，從矩的角度可以判定X的分布是非對稱的.

3 結 論

一般情形下，隨機變量的矩不能完全確定概率分布. 特別地，偏度為0不能得到對稱分布. 本文從隨機變量矩的角度，給出了分布對稱的充分必要條件.

致謝作者非常感謝相關文獻對本文的啟發以及審稿專家提出的寶貴意見.