無窮積分余項與其被積函數比值的收斂階

王鳳瓊

(成都信息工程大學 應用數學學院，成都610225)

1 引 言

以例子形式給出兩個簡單情形的對應比值結束本節.

2 主要結果

對q>0，Gamma函數的余項

有如下結論[5]

Γ(q，x)～xq-1e-x(x→+∞).

(1)

命題1對于c>0，α>0和β>-1， 設

證令u=ctα，則由式(1)，得

因此當x→ +∞時，有

但一般情形， 有

(2)

注2 由洛必達法則， 有

記Fα(x)=Fα，0(x)， 下面考慮它在區間[0，+∞)上的單調性， 依據文[3]定理1和2 的思路可以得到如下結果:

命題2當0<α<1 時Fα(x)在[0，+∞)上嚴格單增， 當α>1時Fα(x)在[0，+∞)上嚴格單減.

證記φα(x)=φα，0(x). 計算得到

F′α(x)=αcxα-1Fα(x)-1=αcxα-1e-cxαfα(x)，

(3)

進而， 有

因此對x∈(0，+∞)， 當0<α<1時有fα(x)>0， 當α>1時有fα(x)<0. 故由式(3)得到Fα(x)在區間[0，+∞)上的單調性.

將命題1的結論應用到Mittag-Leffler函數[6]， 這個函數與分數階微積分以及分數階微分方程有著緊密關系.

對于Mittag-Leffler函數

文[6]得到

于是當x→ +∞時， 有

(4)

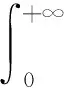
(5)

下面令

(6)

為繼續下去， 需要如下引理([4]， 第三章第10節，P63-64).

于是由式(4)-(6)和引理1， 當x→ +∞時有

其中最后一個等價由式(1)得到. 可見， 仍然與β無關.

3 級數情形

引理2[7](Stolz定理) 設兩個實數列{xn}，{yn}滿足:

(ii) {yn}嚴格遞減；

證當x→0時有(1+x)θ-1～θx， 其中θ為一個常數. 由引理2， 有

(7)

從而

所以

所以

故

4 結 論

致謝本文得到高等學校大學數學教學研究與發展中心2019年項目和成都信息工程大學教改項目的支持， 文獻[3，4，6]給予本文很大的啟示， 審稿人的意見改進了本文， 在此一并表示感謝!