一道數(shù)學考研試題的探討

戴立輝， 黃建吾， 黃 鋒

(閩江學院 數(shù)學與數(shù)據(jù)科學學院，福州350108)

1 引 言

2013年全國碩士研究生入學考試數(shù)學一、二中均有如下試題.

試題設奇函數(shù)f(x)在[-1，1]上具有二階導數(shù)，且f(1)=1，證明：

(i)存在ξ∈(0，1)，使得f′(ξ)=1；

(1)

(ii)存在η∈(-1，1)，使得f″(η)+f′(η)=1.

(2)

此試題的解答可參考文獻[1].受文獻[2]的啟發(fā)，本文將從試題結(jié)論的推廣、相關(guān)新的結(jié)論等方面對該試題進行探討.

2 推 廣

由上述試題知，f(x)在[-1，1]上為奇函數(shù)，故由f(1)=1知f(0)=0，f(-1)=-1.但反之，若f(x)滿足：f(0)=0，f(1)=1，f(-1)=-1，則f(x)未必一定是奇函數(shù).以下將在此相對較弱的條件下對試題進行探討.

首先給出試題的推廣.

試題推廣設函數(shù)f(x)在[-1，1]上具有二階導數(shù)，且f(0)=0，f(1)=1，f(-1)=-1，若n≥0為自然數(shù)，λ為任意實數(shù)，則

(i) 存在ξ∈(0，1)，使得

f′(ξ)=1-λ+λ(2n+1)ξ2n；

(3)

(ii) 存在η∈(-1，1)，使得

f″(η)+f′(η)=λ(2n+1)η2n-1(η+2n).

(4)

證令φ(x)=f(x)-λx2n+1，-1≤x≤1，則φ(x)在[0，1]上可導，故由Lagrange中值定理知，存在ξ∈(0，1)，使得

φ(1)-φ(0)=φ′(ξ)，

而φ(0)=0，φ(1)=1-λ，φ′(x)=f′(x)-λ(2n+1)x2n，故可得

f′(ξ)=1-λ+λ(2n+1)ξ2n.

(3)

同理，由φ(0)=0，φ(-1)=-(1-λ)及Lagrange中值定理知，存在ξ0∈(-1，0)，使得

φ(0)-φ(-1)=φ′(ξ0)，

即

(5)

由式(3)，(5)知

(6)

再令ψ(x)=[f′(x)-λ(2n+1)x2n]ex，-1≤x≤1，則由式(6)知ψ(ξ)=ψ(ξ0)=0，又ψ(x)在[-1，1]上可導，故由Rolle定理知，存在η∈(-1，1)，使得ψ′(η)=0，而

ψ′(x)=[f″(x)-2λn(2n+1)x2n-1]ex+[f′(x)-λ(2n+1)x2n]ex，

且ex>0，故有

f″(η)+f′(η)=λ(2n+1)η2n-1(η+2n).

(4)

特別地，在式(3)，(4)中取λ=1，n=0即可得到式(1)，(2)，因此式(3)，(4)是式(1)，(2)的推廣.

3 若干新的結(jié)論

結(jié)論1設函數(shù)f(x)在[-1，1]上具有二階導數(shù)，且f(0)=0，f(1)=1，f(-1)=-1，若n≥0為自然數(shù)，λ為任意實數(shù)，則存在μ∈(-1，1)，使得

f″(μ)=2λn(2n+1)μ2n-1.

(7)

證由前面的式(6)知

(6)

其中0<ξ<1，-1<ξ0<0.

由于f(x)在[-1，1]上二階可導，故對函數(shù)h(x)=f′(x)-λ(2n+1)x2n在[ξ0，ξ]上運用Rolle定理知，存在μ∈(ξ0，ξ)?(-1，1)，使得h′(μ)=0，即

f″(μ)=2λn(2n+1)μ2n-1.

(7)

注 由于n≥0為自然數(shù)，λ為任意實數(shù)，因此由式(7)可得出許多關(guān)于f(x)的結(jié)論.

例如，取λ=0，則由式(7)知，存在μ∈(-1，1)，使得

f″(μ)=0.

(8)

由于μ∈(-1，1)，故|μ|≤1，從而由式(7)知，存在μ∈(-1，1)，使得

|f″(μ)|≤2n(2n+1)|λ|.

(9)

由λ的任意性，令2n(2n+1)|λ|=|λ0|，則由式(9)可知，對任意實數(shù)λ0，存在μ∈(-1，1)，使得

|f″(μ)|≤|λ0|.

(10)

當然，由式(10)也可知式(8)成立，或式(10)是式(8)的推廣.

結(jié)論2設函數(shù)f(x)在[-1，1]上具有二階導數(shù)，且f(0)=0，f(1)=1，f(-1)=-1，則在(-1，1)內(nèi)存在不同的兩點μ1，μ2，使得

f′(μ1)=f′(μ2).

(11)

證由Lagrange中值定理知，存在μ1∈(-1，0)，μ2∈(0，1)，使得

1=f(0)-f(-1)=f′(μ1)， 1=f(1)-f(0)=f′(μ2).

故由以上兩式知f′(μ1)=f′(μ2)，即式(11)成立.

注 由式(11)及Rolle定理又可得到式(8).

結(jié)論3設函數(shù)f(x)在[-1，1]上具有二階導數(shù)，且f(0)=0，f(1)=1，f(-1)=-1，則

(i) 在(-1，1)內(nèi)存在兩個不同的點ξ1，ξ2，使得

f(ξ1)+f(ξ2)=-ξ1-ξ2；

(12)

(ii)在(-1，1)內(nèi)存在四個不同的點η1，η2，η3，η4，使得

f′(η1)f′(η2)=f′(η3)f′(η4).

(13)

證令u(x)=f(x)+x+1，-1≤x≤1，則u(-1)=-1<0，u(0)=1>0，由連續(xù)函數(shù)的零點存在定理知，存在ξ1∈(-1，0)，使得u(ξ1)=0，即

f(ξ1)=-ξ1-1.

(14)

由Lagrange中值定理知，存在η1∈(-1，ξ1)，η2∈(ξ1，0)，使得

f(ξ1)-f(-1)=(ξ1+1)f′(η1)，f(0)-f(ξ1)=-ξ1f′(η2).

利用式(14)得

故有

f′(η1)f′(η2)=1，

(15)

其中-1<η1<η2<0.

再令v(x)=f(x)+x-1，0≤x≤1，則v(0)=-1<0，v(1)=1>0，從而存在ξ2∈(0，1)，使得v(ξ2)=0，即

f(ξ2)=1-ξ2.

(16)

由式(14)、(16)可得

f(ξ1)+f(ξ2)=-ξ1-ξ2，

(12)

其中-1<ξ1<0<ξ2<1.

再由Lagrange中值定理知，存在η3∈(0，ξ2)，η4∈(ξ2，1)，使得

f(ξ2)-f(0)=ξ2f′(η3)，f(1)-f(ξ2)=(1-ξ2)f′(η4).

利用式(16)得

故有

f′(η3)f′(η4)=1，

(17)

其中0<η3<η4<1.

由式(15)，(17)即得

f′(η1)f′(η2)=f′(η3)f′(η4)，

(13)

其中-1<η1<η2<η3<η4<1.

結(jié)論4設函數(shù)f(x)在[-1，1]上具有二階導數(shù)，且f(0)=0，f(1)=1，f(-1)=-1.

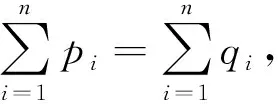
(18)

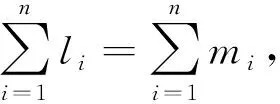
(19)

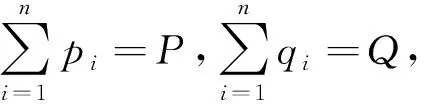
在[xi-1，xi]上對f(x)運用Lagrange中值定理知，存在ξi∈(xi-1，xi)，使得

上式對i從1到n求和，得

即

(20)

其中-1<ξ1<ξ2<…<ξn<0.

同理可得

即

(21)

其中0<η1<η2<…<ηn<1.

-1=y0

取x0=-1，xn=0，在[-1，0]上對連續(xù)函數(shù)f(x)運用介值定理知，存在x1∈(-1，0)，使得f(x1)=y1.在[x1，0]上對f(x)再運用介值定理知，存在x2∈(x1，0)，使得f(x2)=y2.依次下去，可得x3

在每個小區(qū)間[xi-1，xi]上對f(x)運用Lagrange中值定理知，存在λi∈(xi-1，xi)，使得

yi-yi-1=f(xi)-f(xi-1)=f′(λi)(xi-xi-1)，

從而

或

上式對i從1到n求和，得

(22)

其中-1<λ1<λ2<…<λn<0.

作上述類似的處理，可得

(23)

其中0<μ1<μ2<…<μn<1.

4 應 用

文中的結(jié)論有很多應用，限于篇幅，僅舉一例予以說明.

例1設函數(shù)f(x)在[-1，1]上具有二階導數(shù)，且f(0)=0，f(1)=1，f(-1)=-1，λ0為任意實數(shù)，證明方程x2f″(x)+4xf′(x)+2f(x)=λ0x3在(-1，1)內(nèi)至少有一個根.

證令g(x)=x2f(x)，則g(x)在[-1，1]上具有二階導數(shù)，且g(0)=0，g(1)=1，g(-1)=-1.

在結(jié)論1的式(7)中用g(x)代替f(x)并取n=2，由于g″(x)=x2f″(x)+4xf′(x)+2f(x)，因此存在μ∈(-1，1)，使得

μ2f″(μ)+4μf′(μ)+2f(μ)=20λμ3.

由λ的任意性，故對實數(shù)λ0，有

μ2f″(μ)+4μf′(μ)+2f(μ)=λ0μ3.

所以方程x2f″(x)+4xf′(x)+2f(x)=λ0x3在(-1，1)內(nèi)至少有一個根.

5 結(jié) 論

對已有結(jié)論的條件進行弱化處理后，討論是否仍具有原來的結(jié)論并考慮其推廣，這將會使得我們的研究更加深入透徹.

致謝作者非常感謝相關(guān)文獻對本文的啟發(fā)以及審稿專家提出的寶貴意見.