基于PCA-TrICP的多源點云無縫三維重建

劉德兒,劉 鵬,肖 健

(1.江西理工大學建筑與測繪工程學院,江西 贛州 341000;2.江西理工大學外語外貿學院,江西 贛州 341000)

1 引 言

隨著城市化建設的不斷推進,構建智慧城市已經成為提升城市競爭力的主要方法,因此對建筑物的精細化建模也提出更高的要求[1]。無人機傾斜攝影能夠獲取建筑物俯視角度及立面豐富的表面紋理信息,而后使用高效的重建算法將多視角的影像解算出空間結構信息,從而得到三維模型[2]。可如今城市建筑的密集化對建筑立面造成的遮檔和光線的削弱,使得建筑立面信息的采集不夠完整,因此模型精度也將受到影響,容易出現空洞和拉花。因此,使用跨源數據構建完整的精細化模型將是未來的發展趨勢[3-4]。

融合配準[5]是三維重建流程中的核心步驟,如今的主流方法為粗配準和精確配準算法相結合[6-7]。如劉劍等[8]人在計算快速點特征直方圖(Fast Point Feature Histograms,FPFH)的局部特征信息描述符后,與三角網相結合,使特征提取問題簡潔化,因此能夠提高特征點的粗匹配的效率；田青華等[9]人提出了將方向直方圖簽名描述子(Signature of Histograms of OrienTation,SHOT)和空間位置相結合,再采用最小方差法尋找正確的對應點對估算轉換關系；秦楠楠等[10]人利用主成分分析(Principal Component Analysis,PCA)得到點云數據的特征向量和質心,從而對點云數據進行空間變換,得到初始匹配結果；劉江[11]使用數據中心重合法的粗配準方法得到初始位置。精確配準算法應用最多的是迭代最近點(Iterative Closest Point,ICP)算法,由Besl[12]等人提出,是一個拼接效果極佳的算法。針對ICP算法的優缺點,衍生出許多改進算法。文獻[13]使用最優節點優先算法來提升K-D樹對鄰近點的搜索速度,降低計算復雜度,從而提高迭代計算的效率；Chetverikov[14]等人提出TrICP(TrimmedIterative Closest Point,TrICP)算法,計算速度快,對于重疊區域低的數據具有較高的魯棒性。以上配準方法大多是針對數據完整、重疊率高的條件下進行的,但是對于缺乏對稱性和低重疊率的數據,則不能保證其適用性。

為獲取完整的三維模型,本文將融合傾斜影像和激光點云數據用于建筑物的無縫三維重建。其中三維激光點云和航拍影像屬于異維異質數據,故先將傾斜影像幾何重構生成影像點云再與激光點云融合建模。本文提出使用PCA方法確定跨源點云的姿態方向對齊,然后利用幾何中心重合法完成數據矯正,最后運用TrICP算法進行精確配準,獲得高精度的轉換關系,最終得到數據完整的無縫三維模型。

2 實驗數據準備

本文實驗數據為江西理工大學校本部圖書館。通過圖1可以看出受高大樹木及其他建筑的遮擋,使得數據采集有著不小的難度。使用獨立的數據采集方法,會不可避免地出現數據缺失,所以此建筑的數據可以很好地驗證本文的三維重建方法。

圖1 建筑物實景

2.1 激光點云預處理

激光點云數據由Riegl公司型號VZ1000的三維激光掃描儀采集獲得,由于高大數木對建筑立面遮擋嚴重且建筑物形狀復雜,故掃描站次較多。

將建筑點云源數據進行相應的預處理[15-16],首先對數據的離群點去噪,而后拼接配準,并手動分割出圖書館點云數據。運用文獻[16]的方法去除噪聲,該方法主要運用二維的Gamma分布,將鄰域均值以及鄰域距離的變化斜率作為兩個限制條件剔除噪聲點。通過手動選取同名點粗配準和ICP精確配準。手動配準時根據兩個站點掃描場景的重疊區域挑選出至少4對同名點,隨之計算出變換矩陣,將第2站點數據轉換到第1站點坐標系中,然后使用ICP算法實現兩個站點的精確拼接,以此逐步拼接。為避免累積誤差,依次將第3,4,…,12站的數據轉換到第1站點云數據的坐標系中,即所有站點的數據都處于統一的全局坐標系中。完整的激光點云數據如圖2所示。

圖2 激光點云預處理拼接

2.2 基于尺度約束的影像點云獲取與預處理

校園的傾斜影像通過搭載五鏡頭的無人機航拍采集獲取,采集前應預先制訂好航行路線,設置相應的重疊度參數,選定空曠的起降區域。為了更好的驗證本文三維重建方法,從拍攝的海量影像中挑選出含有此建筑的影像179張,經過現場及后期檢查,獲取的影像清晰容易辨別,亮暗適中,可用于后期航片解算。

傾斜攝影有著4個傾斜角度鏡頭,因此影像的同名點數量增多,雖然計算復雜度增加,但計算精度得到提升。CotextCapture軟件具備高效的匹配算法以及區域切塊處理的技術,可以輕松地完成高計算復雜度的任務。將挑選出的影像加載進CotextCapture軟件的新建工程中,剔除不合格影像和勻光勻色處理。為了保證影像點云與激光點云的尺度一致,在進行空中三角測量計算之前加入尺度約束,從而降低尺度問題引起的配準難度。為方便后續三維重建處理,對影像點云手動分割修整去除目標建筑物以外的物體。高密度點云如圖3所示,可以看出建筑立面的數據缺失嚴重。

圖3 影像處理結果

3 多源點云數據無縫融合

3.1 基于主成分分析的粗配準

3.1.1 PCA坐標系求解

PCA作為一種經常使用的數據分析方法,是通過將高維的原始數據降成各維度線性無關的低維數據,從而有利于提取數據的特征分量,將方差較小的數據特征忽略掉,達到降維處理的目的,突出數據最主要的方面,甚至可以實現去噪的效果。本文對于點云數據進行降維分析只需找到相互垂直的三個主要特征分量,即對方差貢獻最大的三個向量,用以對應點云的分布方向以及表達點的空間位置。

(1)

(2)

(3)

對Cov(X,Y,Z)進行奇異值分解,得到特征值λi對應的特征向量wi,并對特征值λi進行降序排列得到對角矩陣∑=diag[λi,λ2,λ3],和兩組正交矩陣U(3×3)、V(3×3)。

Cov(X,Y,Z)=U∑VT

(4)

其中,正交矩陣U由∑對應的特征向量組成,表示點云PCA坐標系三個主軸的方向向量。U中三個向量分別表示點云三個主元方向,并且三個向量相互垂直,如圖4所示,其中第一個向量表示點在空間分布趨勢最大的方向。在提取出主成分后,將激光點云和影像點云轉換到同一個坐標系下,其中轉換關系就是協方差矩陣的對應關系,對兩個點云經過全局進行轉換,從而達到點云粗配準的效果。

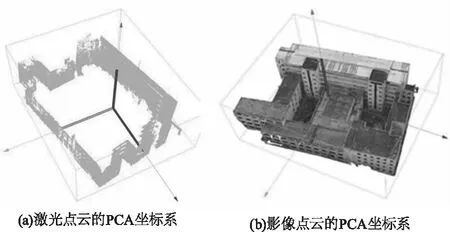
圖4 跨源點云的主元方向

3.1.2 矯正PCA坐標系

通過航空影像獲取的影像點云在建筑體表面分布均勻,密度較高,且呈現單層次分布；而三維激光掃描儀工作時受到站點視角以及障礙物遮擋等情況的影響,使得激光點云在空間中的分布并不均勻,有的區域密度很高,有的區域點云分布稀少,以及建筑物頂部數據的缺失。所以通過這兩種方式獲取的點云數據具有不一樣的特性,從而導致兩個點云數據PCA配準的結果并不是很準確。其中坐標軸的方向大致平行,但是偶爾出現反向的情況,以及數據質心的偏差。

首先通過點云的包圍盒來矯正PCA坐標系的原點。點云的外包盒一般有球形、方向包圍盒和軸向包圍盒AABB(Axis-Aligned Bounding Boxes,AABB)三種,其中AABB包圍盒是平行于坐標軸,即每一個面都有與其相互垂直的坐標軸。由于PCA配準后兩個點云的主方向大致確定,不再將其方向二次旋轉,且AABB包圍盒對方向很敏感,所以選擇AABB包圍盒進行二次匹配。

1)使用源點云A和目標點云B的包圍盒頂點的極值坐標計算包圍盒幾何中心μa和μb,其極值為點云包圍盒的頂點坐標的極大值AMax、BMax和極小值AMin、BMin。

(5)

(6)

2)得到幾何中心μa和μb后,計算它們的差值,也就是源點云的二次平移向量T′。

(7)

3)利用新計算的二次平移向量T′對源點云進行平移。

(8)

式中,A′為源點云平移后的數據點集。

對于三個軸向的正反方向情形將引起23種對應關系,本文將設定一個距離閾值d,使用K-D樹加速搜索對應點對,小于該閾值d的對應點將被標記,然后計算被標記的點云數量所占目標點云PM的重疊率γ=Ir/PM,比較這8種對應關系的重疊率γ大小,將重疊率最大的對應關系作為主軸的方向。

(9)

將兩類點云的幾何中心匹配和矯正坐標軸方向,可以減小兩類點云的歐式距離,縮小粗配準的偏差,此方法也能夠得到兩類點云更大區域的重疊,較優的粗配準效果,為精配準提供更佳的位姿狀態。

3.2 Trimmed ICP精確配準算法

經典ICP配準算法主要思想是通過源點云向目標點云尋找歐氏距離最近的點,使每一個源點都有著對應目標點,解算出變換矩陣完成轉換；然后進行第二次尋找最近點,再解算出新的變換矩陣完成轉換；如此往復迭代,直到滿足迭代終止條件。

TrICP算法則是使用重疊率Υ來自適應的匹配算法,將非匹配點去除以改進ICP算法。從算法結果來看,與原算法主要的區別在于可以通過不同的重疊率來影響配準結果；從算法原理來看,改變了MSE的統計方法,即算法的全過程都使用截斷最小二乘(The Least Trimmed Squares,LTS)計算誤差平方和。如式(10)所示,當h=n時,把所有的殘差考慮在內,等價于原始算法。

(10)

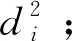
qcl(i,R,T)=argmin||q-pi(R,T)||

(11)

(12)

(13)

(14)

式中,Sumdi代表Npo個重疊點對的殘差平方和,本次迭代的MSE=Sumdi/Npo,隨之判斷是否滿足終止條件,選擇是否繼續迭代計算；

(3)通過奇異值分解計算出變換關系(R,T),使得滿足Npo點對的Sumdi最小；

(4)將源點云按照變換關系(R,T)向目標點云方向運動,重復步驟(1)。

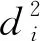
4 實驗結果分析

4.1 實驗點云數據抽稀

為了驗證本文算法對于跨源數據三維重建的有效性,將在Inteli5 CPU、Nvidia1060顯卡以及16GB內存的PC設備上進行實驗,并使用PCL(Point Cloud Library)庫編程實驗進行分析。使用經過了預處理的激光點云和傾斜影像數據,如圖3和圖4所示,并通過體素網格下采樣方法對點云數據進行抽稀,最終用于驗證本文算法的激光點云數據的數目為998545,影像點云數目為1428361。

4.2 粗配實驗及精度分析

跨源點云經過預處理后,首先進行各自的PCA分析,計算出兩類點云各自質心以及三個最大的特征向量,進行點云旋轉和平移,完成PCA變換。其中激光點云質心O1(9.9412,47.6741,6.2562),影像點云質心O2(-20.5584,-47.7046,9.5665)。通過PCA變換,如圖4,質心O1和O2將作為新坐標系的原點,并完成幾何中心的匹配。比較了另外兩種常見算法,以及相應的精度比較。由于跨源點云的差異性,配準后也難以使兩個點云完美的貼合在一起,且不一樣的精度統計方法,得到的精度結果也大不一樣。考慮到本文實驗數據重疊率低的特點,即源點云不是目標點云的子集,且各自有較大面積的非對應區域。所以本文在精度統計時,將非對應點剔除,統計對應點的距離,然后使用計算出的均方根值(RMS)作為精度表達。

對實驗數據進行多種常規的點云粗配準方法實驗后,如圖5所示,展示點云變換后的正視、側視和俯視配準效果,(a)為建筑正視圖；(b)為建筑側視圖；(c)為YOZ平面切片。其中正態分布變換(NDT)對于跨源點云的粗配準效果不佳,遠達不到精配準的初始位姿要求。基于FPFH的采樣一致性粗配算法對跨源點云具有一定的適用性,只是對于本實驗數據需要設置較大的計算參數。本文的粗配方法為經過PCA變換后矯正點云中心和軸向,使得跨源點云較為緊密的拼接在一起,從圖中觀察可知效果明顯優于另外兩種方法,并由表1可知,初始位姿誤差也遠遠低于另外兩種方法,達到了0.32 m,將其作為后續精配準工作的初始位姿。

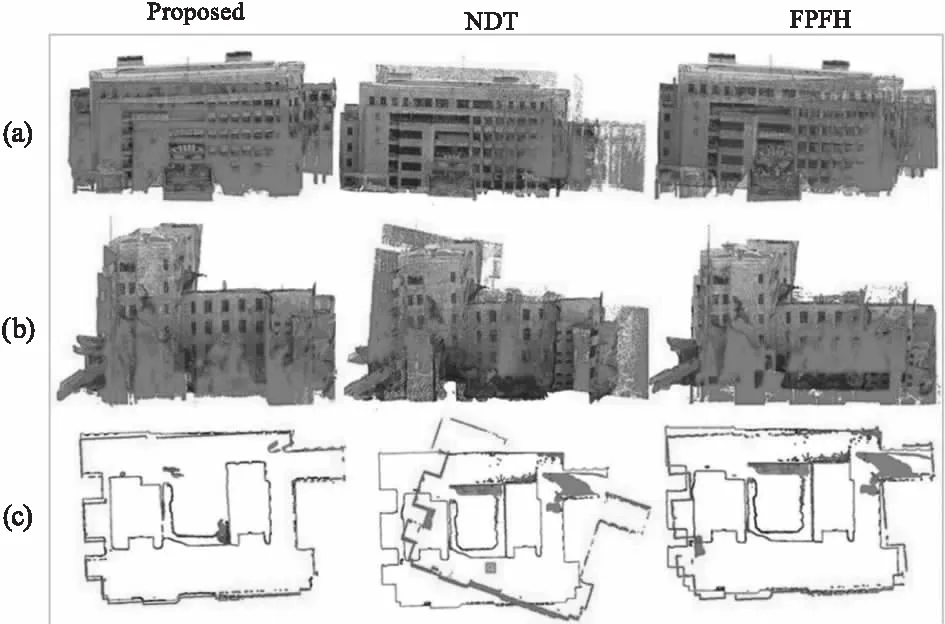
圖5 粗配準實驗結果對比

表1 初始配準精度比較

4.3 精配實驗及精度分析

在激光點云得到初始位姿后,使用參數為60 %重疊度和最大30次迭代次數的TrICP算法對其進行精確配準,并與參數為最大30次迭代次數的經典ICP算法、GICP算法和FPFH+NDT算法[17]結果進行比較。如圖6所示,在本文粗配準方法獲得的初始位姿條件下,比較了ICP、GICP和TrICP精配結果的局部差異。可發現三種算法對俯視角的配準效果基本一致,但是多個立面的頂部區域有著細微的差異,可以看出在經典ICP算法結果中,激光點云整體上移,陷入了局部最優。

在表2的誤差分析中,統計了各個立面之間的獨立誤差。其中文獻[17]使用的FPFH+NDT算法對于本文實驗效果較差,不適用于此類跨源點云的配準工作。對NDT算法分別進行粗配準和精配準的實驗可以看出,NDT算法同樣需要一個初值才能獲得更好的運行效果。在三個立面的誤差分析中,正立面和側立面的誤差,TrICP要明顯小于ICP和GICP；背立面的誤差,TrICP卻大于ICP和GICP。在整體精度中,TrICP的精度相對于傳統ICP,總體提高了53.5 %,達到了0.0811 m。

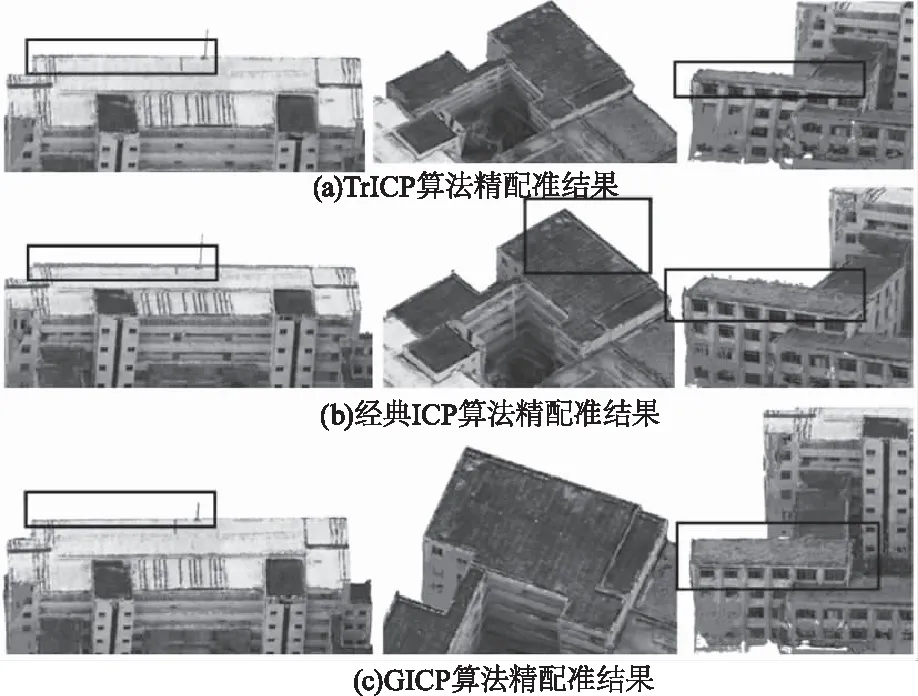
圖6 精配準的細節對比

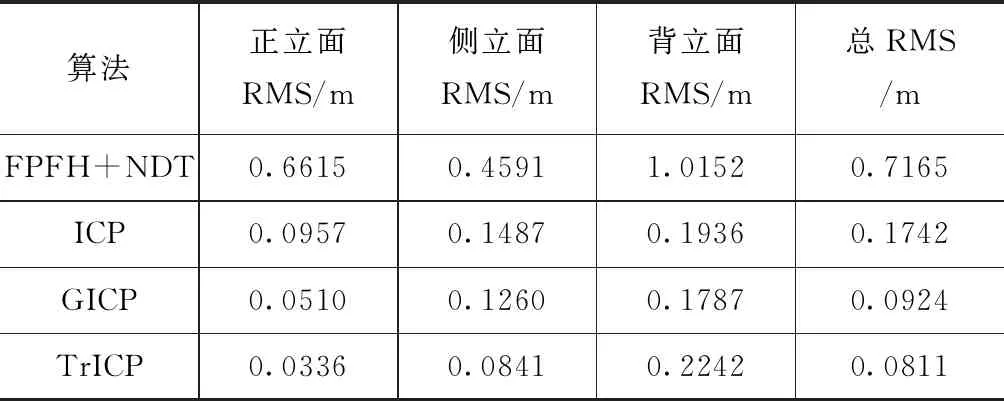
表2 精配準誤差分析(包括不同立面的單獨誤差,總誤差)

圖7所示為最終跨源點云的配準結果。配準誤差較大的部分點云主要集中在靠近地面區域,誤差偏小的點大多分布在遠離地面的建筑立面上,因此說明傾斜影像獲取立面信息的準確度不一致。影像點云的數據缺失在建筑兩側的立面區域最為嚴重,圖7中顯示激光點云能夠對其予以修補。總的來說,配準誤差由建筑立面從上往下逐漸增大。考慮到激光雷達的高精度掃描,影像點云越接近于地面時,獲取的立面信息偏差也增大,跨源點云的配準精度也隨之降低。從實驗結果看來,本文通過實驗完成了異維異質的跨源數據配準,對于這類聯合多源數據的三維重建問題具有一定的指導意義。

圖7 精配準結果

5 結 語

本文提出一種跨源數據融合配準的三維重建方法。該方法通過PCA變換后的點云,并用中心匹配來獲取一個較好的初始位姿狀態,然后使用TrICP算法完成精配準工作。針對激光點云數據獲取時受到視角的影響難以獲取建筑頂部信息,以及傾斜影像對立面信息獲取的不完整性,使用兩種數據融合完成三維重建,能夠彌補激光點云視角的限制和傾斜影像在建筑物立面的空洞、紋理扭曲等缺陷,提高建筑物的三維模型的信息完整性。如何消除建筑立面上小下大的誤差分布特點,將是后續的主要研究工作。