黏土地層淺埋盾構隧道開挖面三維穩定性上限分析
李修磊,李金鳳, 楊 超
(1. 重慶交通大學 河海學院,重慶 400074; 2. 三峽大學 三峽庫區地質災害教育部重點實驗室,湖北 宜昌 443002)
隧道開挖時引起應力釋放,開挖面周邊圍巖土體的平衡被打破,因而需要足夠支撐保證其的穩定。盾構工法在軟弱地層隧道施工中得到廣泛使用。根據盾構機的類型,可以采用壓縮空氣、土壓力或泥漿提供支撐均勻分布在掌子面上。如果提供的支撐力不足以平衡外部土壓力和水壓力,開挖面周圍土體有向隧道內部涌入的可能而變得不穩定甚至坍塌,表現為地表沉陷。合理控制開挖面的支護壓力,不僅能夠保證開挖面的穩定,還能有效降低隧道施工引起的地表變形及其對周圍建筑物的影響。
隧道掌子面的穩定性分析是保證淺埋盾構隧道安全施工的關鍵,主要內容在于確定隧道掌子面的極限支撐力[1-2]。如2002年深圳地鐵一期4號線采用土壓平衡式盾構機掘進時引發地面塌陷及鄰近建筑物輕微沉降;廣州地鐵3號線盾構施工中,由于壓力艙內壓力失控,造成地面變形。歸其原因均是由于盾構施工中開挖面支護壓力設計不合理所致, 由此引起了工程界學者對盾構開挖面穩定性的廣泛關注,目前主要的研究方法有室內模型試驗[3-6]、現場實測[7]、理論分析[8-10]及數值計算(如,有限元法[11-12]、有限差分[2,13]和離散元[14-15])等方法。國內學者進行理論分析時,依據工程經驗和室內試驗結果提出各種相應的簡化模型,采用極限分析法或極限平衡法計算開挖掌子面的極限支護壓力。Leca等[9]首次提出了淺埋隧道開挖面失穩的三維破壞機制,由一個或兩個截圓錐體組成,給出了維持盾構隧道開挖面穩定的上、下限解,并由離心機試驗結果證實了模型解答的合理性。在此基礎上,一些學者分別構建了多個剛性截圓錐的開挖面的破壞模式,擁有更多的自由度,通過優化求解開挖面極限支護壓力的上限解答[16-19]。Han等[20]采用同樣的方法考慮了隧道上方含多層土體的情況。Mollon等[10]采用空間離散化技術提出開挖面為圓形破壞形態的三維旋轉破壞機制,并基于上限定理提出了兩種破壞模式的開挖面穩定性分析方法。Kim等[11]在Mollon等[10]方法的基礎上考慮了巖土體的各向異性和非均質性。宋春霞等[21]采用截橢圓柱體構建了多塊體平動破壞模式的掌子面三維穩定性的上限分析方法,改進了破壞模式與隧道開挖面的接觸問題。梁橋等[22]基于筒倉理論和Mohr-Coulomb強度準則,提出了掌子面超前核心土對數螺旋的破壞模式,推導了隧道開挖循環進尺的計算模型。Zhao等[23]認為隧道開挖面服從截圓錐多塊體平移破壞模式,考慮了隧道長度和傾角的影響,基于極限分析上限定理,利用序列二次規劃法得到了支護壓力的最優上限解。也有學者[24-25]引入巖土體的非線性破壞準則,對隧道掌子面的穩定性進行了分析。
基于上述研究,本文認為實際工程中隧道側壁對掌子面有一定的約束作用使得其破壞區域一般不會是完整的圓形,以橢圓形態進行研究更符合實際;上述研究采用的隧道開挖面破壞模式與實際情況存在差距,一定程度上會影響結果的準確性。本文將基于離心機試驗中隧道開挖面的實際破壞形態,提出更接近于實際狀況的破壞機制,利用極限分析上限法,根據虛功原理推導掌子面三維破壞極限支護壓力的解析式,探索各因素(如,巖土體物理參數、超負荷比等)對開挖面穩定性的影響規律。研究成果可進一步完善盾構隧道開挖面的穩定性分析方法,對其設計及施工具有借鑒和參考價值。
1 隧道開挖面的破壞模式
基于相關文獻[5,26]報道的離心機模型試驗結果表明,開挖面超前核心土破壞區主要是剪切破壞所致,拱頂上部拱形的破壞區為較為復雜,可能受拉、剪應力共同作用。因此,上、下兩部分的破壞模式需分別構建。
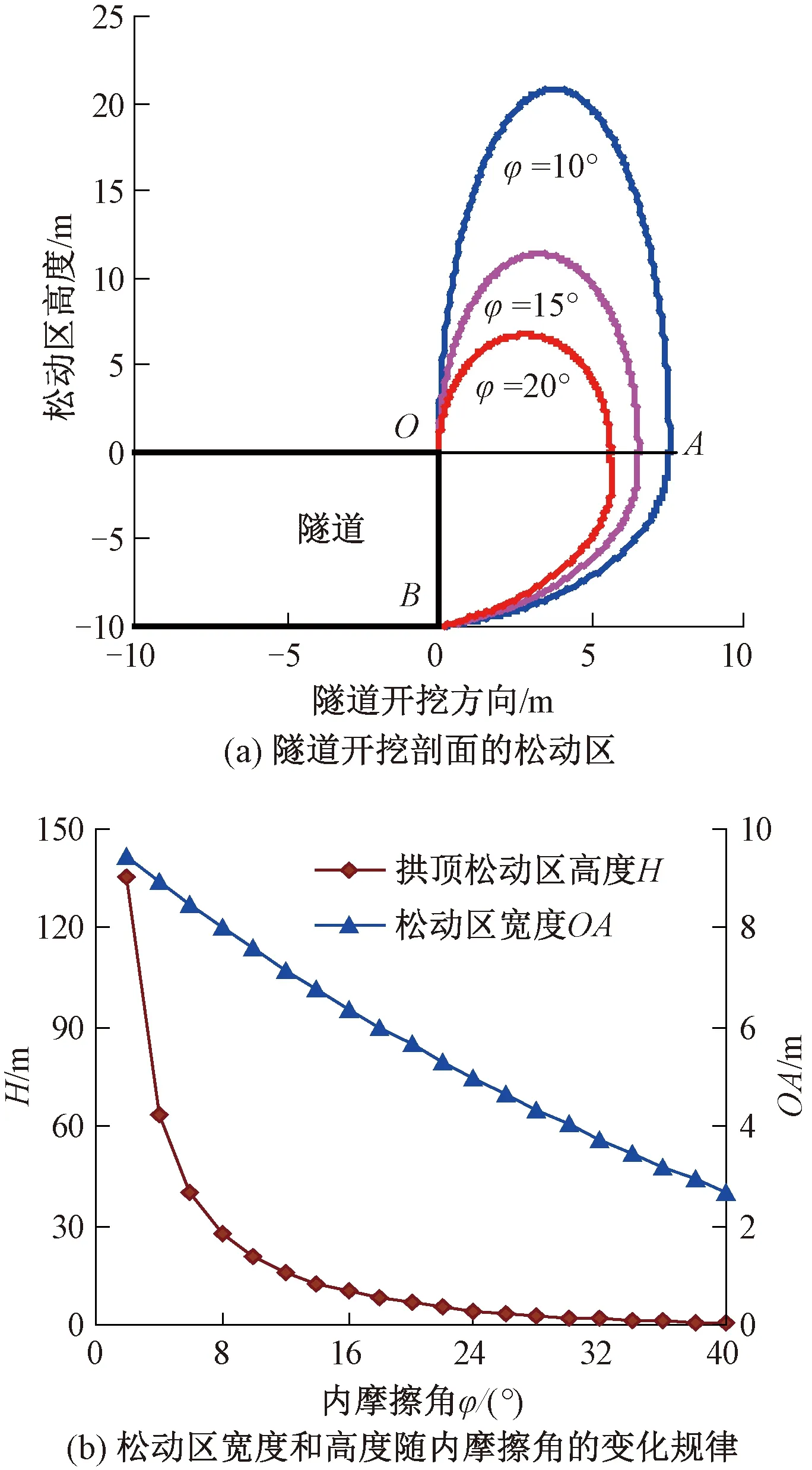
離心機模型試驗結果[5,26]還表明,隧道埋深C與其直徑D的比值一定時,隨著開挖面位移,開挖面土體前方發生變形,導致隧道拱頂區域產生豎向松動,逐漸形成拱形松動破壞區;隨著開挖面繼續位移,拱形松動區逐漸向上發展,最終貫通到地表并出現微小沉降;伴隨著松動區的發展,作用在開挖面上的荷載也在平緩增加[4];隧道埋深超過某一深度且開挖面位移一定時,由于圍巖形成的拱效應使得圍巖壓力僅為隧道周邊某一范圍內的巖體重力,而與深度無關,基于上述分析,開挖面局部失穩和整體失穩時滑裂面縱、橫向的剖面示意圖,見圖1。
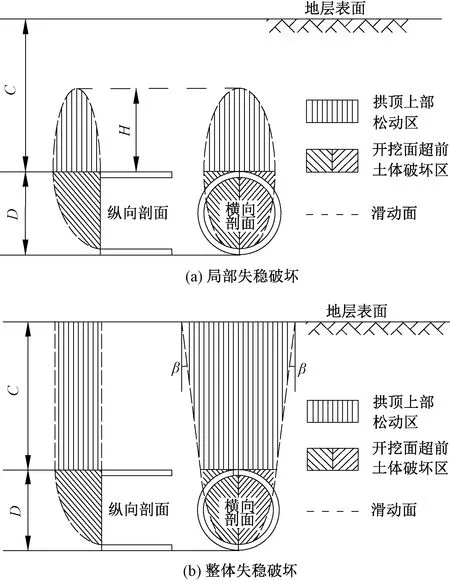
圖1 隧道開挖土體松動區縱、橫向剖面示意圖
2 隧道開挖面的破壞模式三維極限分析法
在考慮開挖面前方及隧道拱頂上部土體荷載效應的基礎上,構建新的掌子面失穩的破壞模式,見圖2。

圖2 隧道開挖面的失穩破壞機制
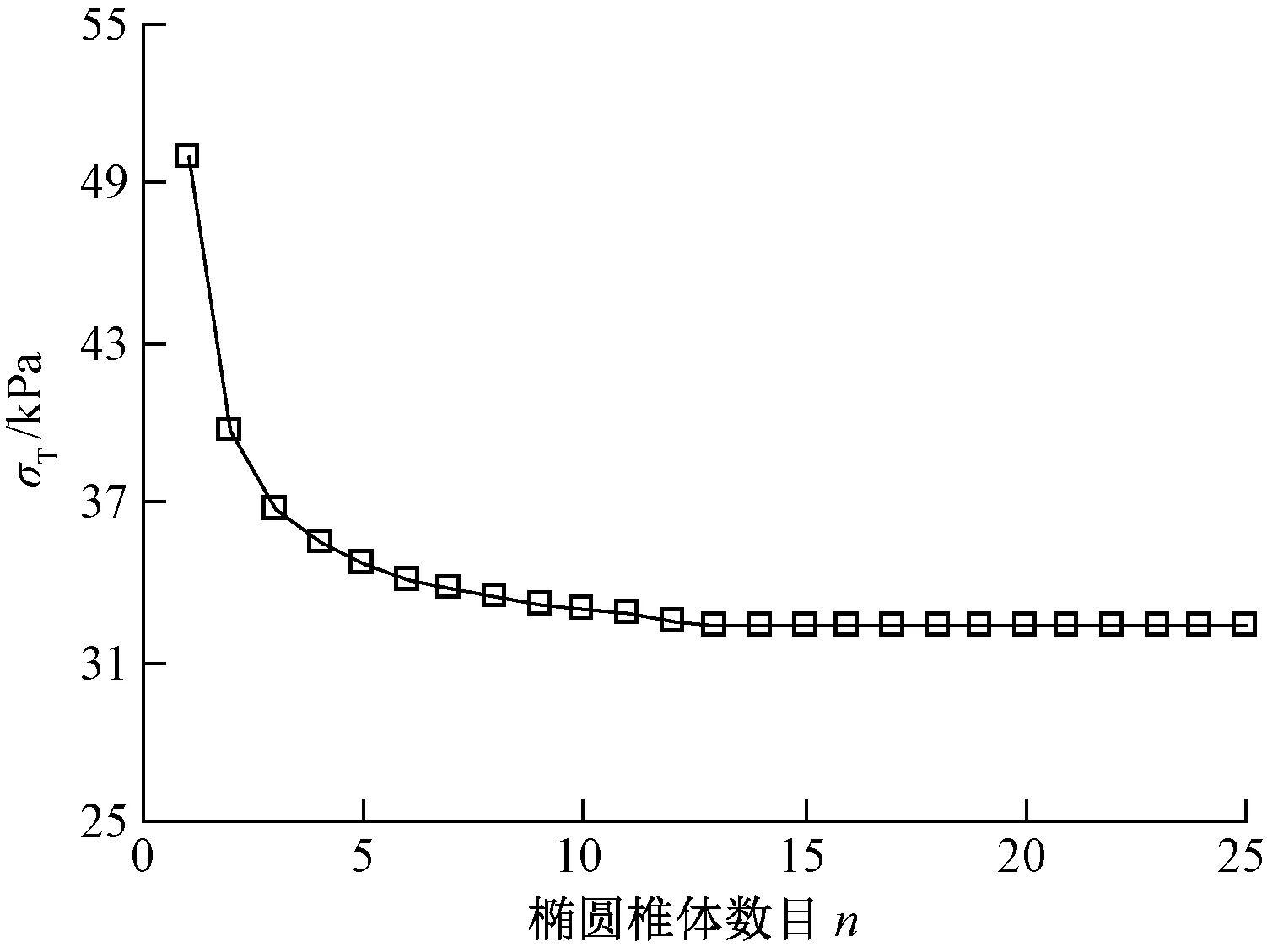
由圖2可知,隧道是一個直徑為D的剛性圓柱體,埋置深度為C,拱頂上部失穩橢圓半球體的高為H,σT為均勻分布在開挖面上的支護壓力,σ0作用在地表的附加應力。土層的黏聚力為c、內摩擦角為φ。由圖2(a)可知,隧道開挖破壞模式由拱頂上覆的半橢圓球體OAE和開挖面前方的橢圓對數螺旋體OAB組成。當上部結構作用力所做的功與橢圓半球體與對數螺旋體四周摩擦產生的能量耗散維持平衡時,開挖面保持穩定,否則開挖面失穩破壞。在三維空間模式下,將開挖面前方松動區的對數螺旋體劃分為n塊,每一塊均是由橢圓錐之間交線截成的斜截橢圓椎體,見圖2(b)。由圖2(b)可知,掌子面前方對數螺旋體破壞區域由多個錐體滑塊組成,基于極限分析上限定理中的機動容許速度場,錐體滑塊的數目一定程度上會影響計算結果的精度。一般而言,錐體滑塊數目越多,越接近實際破壞情況,精確度越高;當滑塊數目達到一定值時,計算精度提高的幅度越小,因而需要合理確定錐體數目。計算參數取自Mellon等[19]中的算例。
2.1 截橢圓錐體幾何尺寸的遞推關系
基于文獻[10,28],隧道掌子面超前核心土呈對數螺旋破壞模式,圖2中曲線AB的方程為
r=Dexp(-θ·tanφ)
(1)
將下部的對數螺旋滑動體劃分為n個截橢圓錐體,每個剛性截橢圓錐體的中心角角度為
(2)
若剛性截橢圓錐體的數目足夠多,即Δθ足夠小,則可以得到足夠光滑的隧道掌子面失穩的三維滑動破壞面。各橢圓椎體的相關特征參數αi為
αi=π/2-βi-φ0i=2,3,…,n,n+1
(3)
隧道掌子面相鄰的第一個橢圓錐與開挖面相交為橢圓形,其長半軸a1、短半軸b1的長度以及該橢圓椎體的高度h1分別為
a1=D/2
(4)
(5)
(6)
式中:每個截橢圓錐體的張開角度為2φ0;α為第一個剛性截橢圓錐體的軸線與水平線夾角,根據三角形的關系得α=0.5π-β1-φ0。由此,可得第一個截圓錐體底面的面積為
(7)
依次類推,可以得到第i個截橢圓錐體底面的長半軸ai、短半軸bi、底面面積Ai以及該橢圓椎體的高hi分別為
(8)
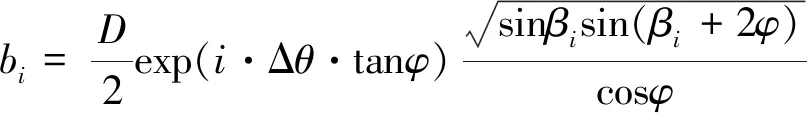
(9)
(10)
(11)
(12)
式中:i=1,2,…,n;βn+1=π/2。
第n+1個橢圓椎體底面的長半軸an+1、短半軸bn+1、底面的面積An+1,以及該橢圓錐體的高hn+1分別為
(13)
(14)
hn+1=2an+1cot2φ
(15)
(16)
2.2 各滑動塊體的幾何參數
由2.1節可知,掌子面前方各截橢圓錐體的側面積Si及其體積Vi的計算公式[9,29]為
(17)
(18)
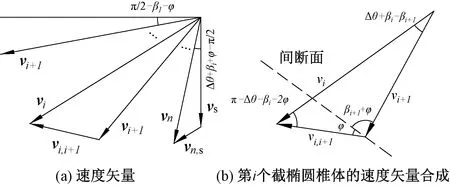
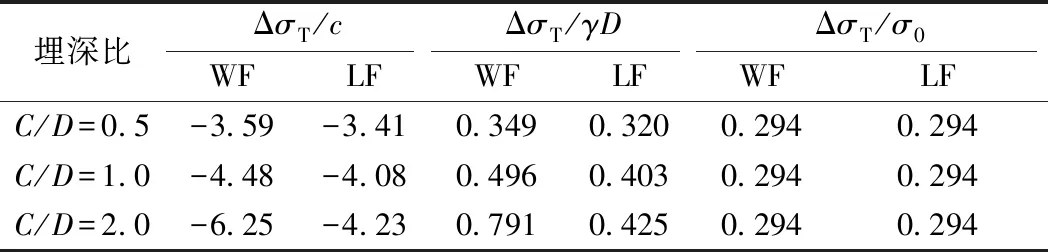
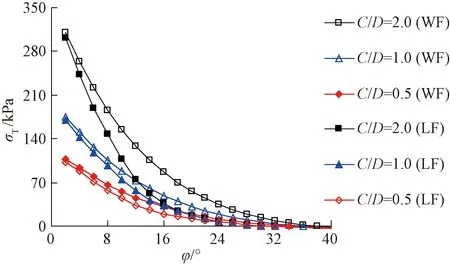
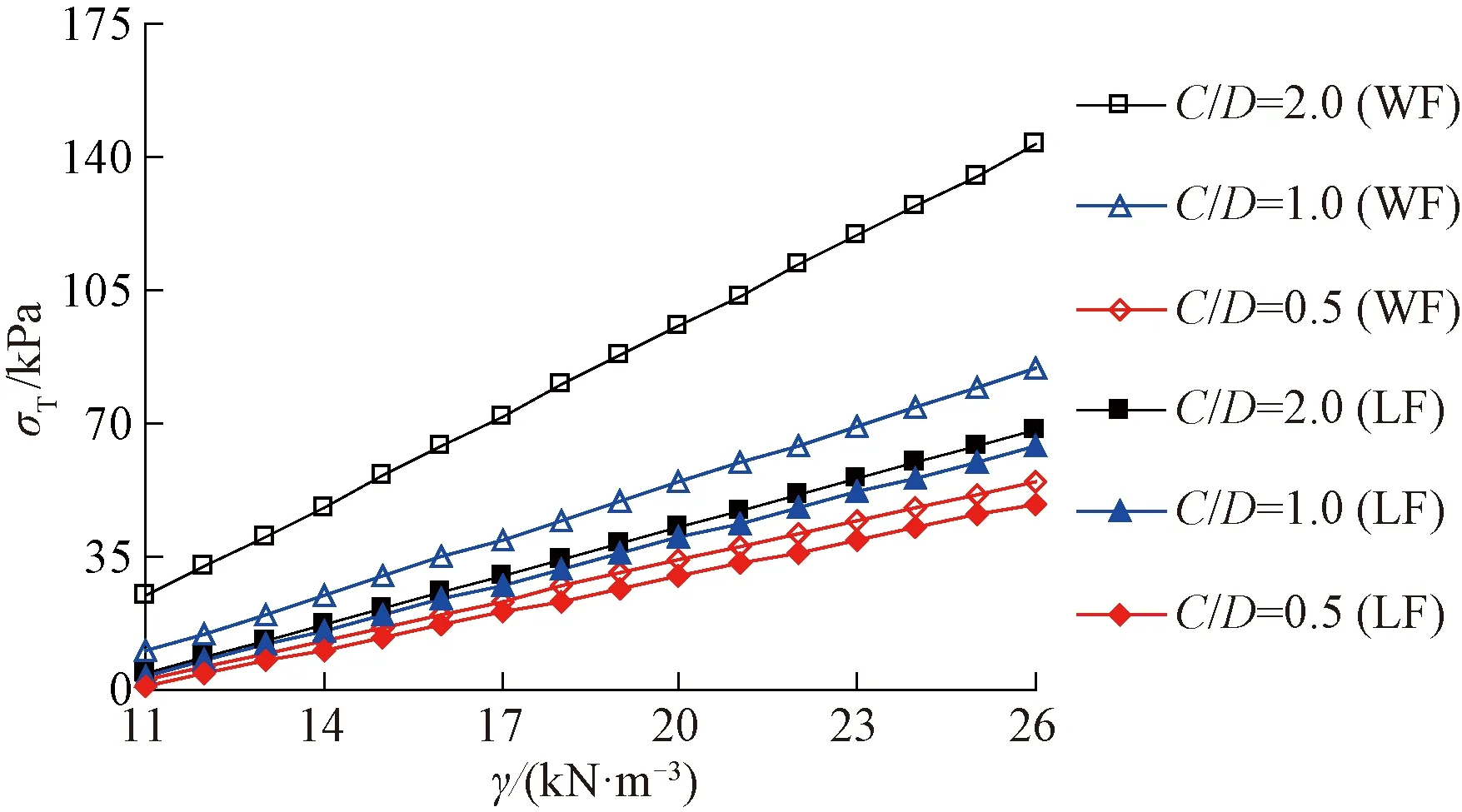
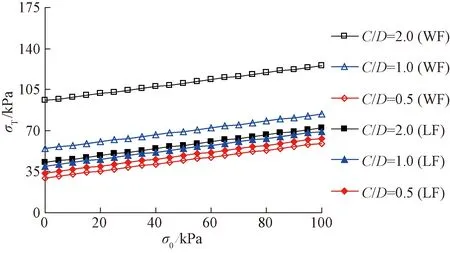
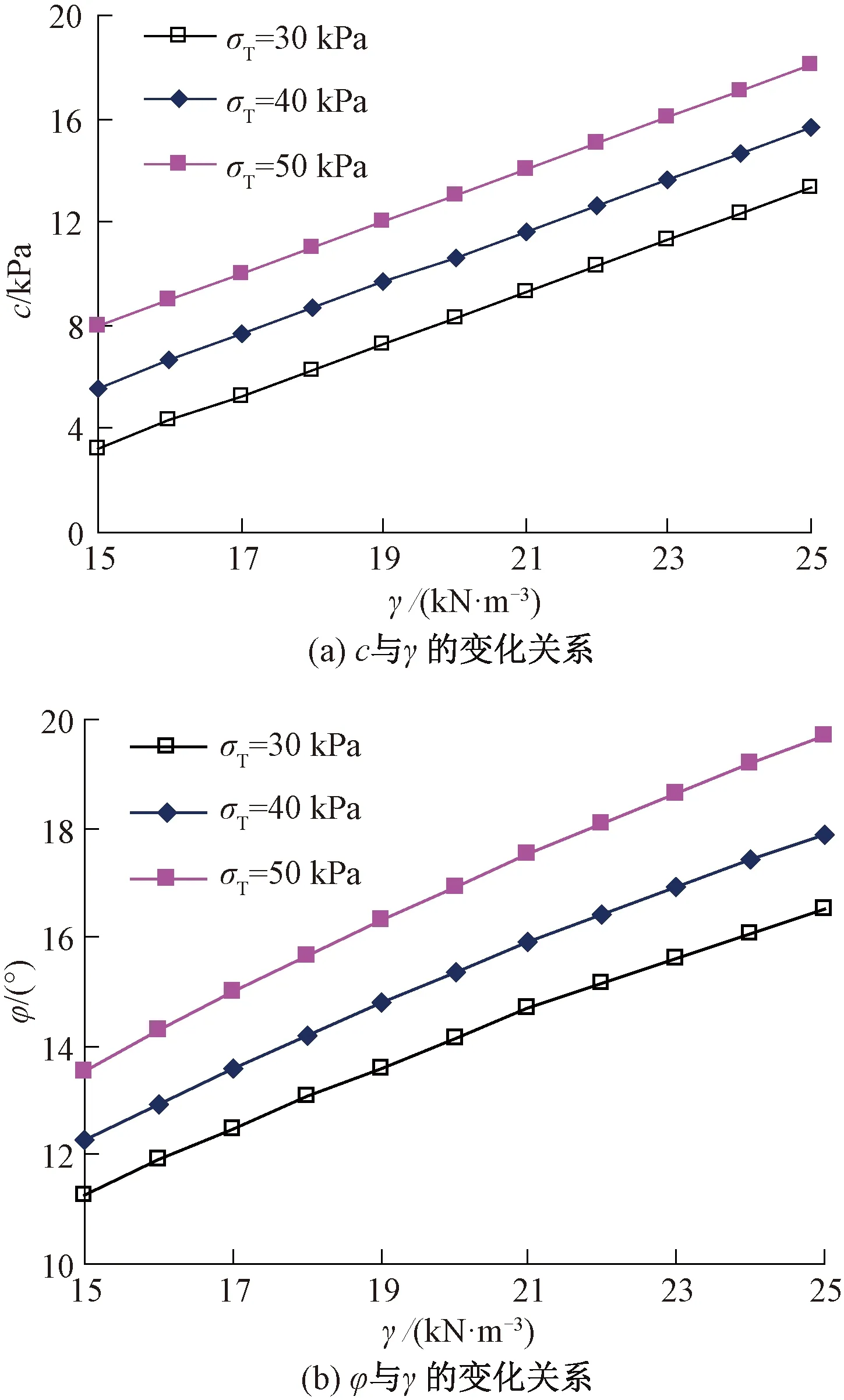
由圖2(a)可知,隧道埋深較大時,拱頂上部松動區位于上覆土體內部(即H (19) (20) 由圖2(b)可知,隧道開挖發生整體失穩,拱頂上部松動土體貫通地表。此時,拱頂上部土體松動區為橢圓柱體,其側面積和體積分別為 (21) VS=πaOA×[bOA+C·tanβ]×C (22) 各間斷面上速度之間的幾何關系見圖3。由圖3可知,各間斷面上速度之間的相對關系為 圖3 三維破壞機制的速度場 (23) (24) (25) (26) 各截橢圓錐體的下滑速度vi與豎直方向的夾角ψi為 ψ1=β1+φ (27) ψi=βi-(i-1)Δθ+φ (28) 式中:i=1,2,…,n。 重力做功WV為變形區土體總重量與速度的乘積,計算式為 (29) 式中:γ為土體的容重;ψi為vi與豎直方向的夾角;VS的作用方向為豎直方向;當隧道埋深較大時,考慮土拱效應忽略式(29)右邊第3項。作用在掌子面上支撐力所做的功WT為 WT=-σTA1v1sin(β1+φ) (30) 根據極限分析上限定理計算相容速度場的內能耗散,圖2所示破壞模式的能量耗散包括各截橢圓錐體速度間斷面上的能量耗散和拱頂上部半橢圓球體表面的能量耗散,DT計算式為 (31) 當機動許可的速度場滿足位移邊界條件時,根據外力做功與內能耗散相等的原理,即DT=WV+WT,得到隧道掌子面三維破壞極限支撐力的目標函數為 (32) 當橢圓錐體數目小于5時,錐體數目對極限支護壓力有顯著影響,當錐體數目大于10時,錐體數目的增加對極限支護壓力計算精度的提高非常有限。考慮耗時影響,本文選取錐體數目為15進行計算分析,橢圓椎體數目對極限支護壓力的影響見圖4。 圖4 橢圓椎體數目對極限支護壓力的影響 對于工況1(土層強度參數為c=7 kPa,φ=17°)和工況2(c=10 kPa,φ=25°),本文計算結果與其他文獻結果的對比情況,見圖5。由圖5可知,工況1時,本文計算結果略低于文獻[18]計算結果的4.8%,但相比文獻[23]和文獻[9]的計算結果分別增加了12.8%、36.6%;工況2時,本文方法計算結果與文獻[9]的計算結果非常接近,要小于文獻[18]和文獻[23]的計算結果。對上述兩種情況,當C/D分別大于0.8和0.3時,拱頂土體松動區位于覆蓋層內部,開挖面極限支護壓力σT為常數,屬于局部破壞,與實際情況相符。通過以上對比分析,說明本文方法的計算結果對土層強度參數變化更敏感,也證實了本文方法的正確性和有效性。 圖5 本文計算結果與其他結果的對比曲線 開挖面發生整體失穩的情況下,考慮橫向剖面拱頂上覆松動土體滑裂面擴散角β的影響時,開挖面極限支護壓力σT隨埋深比C/D的變化規律,見圖6。由圖6可知,擴散角β=0時,σT隨C/D的增加呈線性增加;當β>0時,σT隨C/D的增加呈拋物線形狀增加,且C/D相同時β越大對應的σT越大。原因在于β的增加導致了拱頂上覆土體松動區域的變大,且隨著C/D的增加,土體松動區增加的幅度逐漸增大。由于擴散角β存在不確定性且為淺埋隧道,因而基于筒倉理論以下計算均取β為0進行各參數的影響分析。在分析某一因素影響時,其他參數均保持不變。 圖6 整體失穩時開挖面極限支護壓力隨埋深比C/D的變化規律 (1)隧道埋深的影響 當內摩擦角φ=15°,土層容重γ=20 kN/m3時,土層黏聚力c和內摩擦角φ不同條件下,開挖面極限支護壓力隨埋深比C/D(隧道埋深與直徑的比值)變化關系見圖7。由圖7可知,在發生整體失穩(WF)的情況下,極限支護壓力σT隨埋深比C/D呈線性增加,且土層黏聚力c和內摩擦角φ越大增加幅度越小(即,斜率越小);當發生局部失穩(LF)時,隧道埋深比C/D較小時,σT隨C/D的增加逐漸增大,C/D較大時,σT為定值不再受隧道埋深比的影響,說明此時隧道拱頂上部松動破壞區的高度位于上覆土體內部,由于土體成拱效應使得松動破壞區不再向上延伸,因而上覆土厚度增加不會導致支護壓力的增大。 圖7 埋深比C/D對極限支護壓力σT的影響 本文針對局部破壞的計算情況,與文獻[5]試驗結果和文獻[14]數值計算結果一致。無論是整體破壞和局部破壞,極限支護壓力均隨著黏聚力c和內摩擦角φ的增加逐漸減小;相比局部失穩,整體失穩時所需的極限支護壓力明顯要大很多。 (2)土體強度參數的影響 當γ=20 kN/m3、φ=150°隧道埋深比C/D不同時,土層黏聚力c對極限支護壓力σT的影響見圖8。由圖8可知,隨著c的增加,σT呈線性減小趨勢,且C/D越大減小幅度越大(見表1)。黏聚力c一定時,埋深比C/D越大,整體破壞和局部破壞所需的極限支護壓力σT之間的差距越明顯;反之兩種破壞模式的差距越小。這是因為C/D越小,兩種破壞模式下隧道拱頂上部松動破壞區范圍的圍巖重力差距越小,反之越大。 圖8 土層黏聚力對極限支護壓力的影響 表1 c、γ和σ0對σT變化幅度的影響 當γ=20 kN/m3、C=10 kPa時,極限支護壓力σT與內摩擦角φ之間的變化關系曲線,見圖9。由圖9可知,初始階段極限支護壓力σT隨著內摩擦角φ的增加快速減小,且減小的幅度隨著內摩擦角φ增大逐漸趨于平緩,并最終減小到0;同樣,隧道埋深比C/D越大,兩種破壞模式所需σT的差距越大,反之越小。另外,隧道埋深比C/D為定值的情況下,內摩擦角φ越小或越大(即,φ<5°或φ>30°),整體失穩與局部失穩計算結果的之間差距越小;前者的原因是φ較小導致隧道拱頂上部松動破壞區很高,遠遠超過上覆土層的厚度,使得局部破壞區域和整體破壞區域差別不大;后者是因為內摩擦角φ足夠大時,兩種破壞模式均需要克服很大的能量耗散,所以導致兩種破壞模式得到的極限支護壓力均較小。 圖9 土層內摩擦角對極限支護壓力的影響 當γ=20 kN/m3、C=10 kPa時,內摩擦角不同的情況下,隧道拱頂上部土體松動區高度的變化規律,以及隧道開挖面前方和拱頂上部土體松動破壞區的變化情況,見圖10。由圖10可知,本文計算所得土體松動破壞區形態與試驗結果[5,26]非常接近;隨著內摩擦角的增大,隧道開挖對應的土體松動破壞區逐漸縮小,很好地說明了本文計算結果的合理性。另外,由式(13)、式(15)可知,拱頂上部松動區的高度只與土體的內摩擦角φ有關,不受黏聚力c變化的影響。 圖10 土層內摩擦角對土體松動區范圍的影響 (3)土層容重和地面超載的影響 當C=10 kPa、φ=15°時,隧道開挖面極限支護壓力σT隨土層容重γ的變化關系曲線,見圖11。由圖11可知,整體和局部兩種破壞模式下,極限支護壓力σT隨著γ的增加均呈現出線性增加的趨勢,且隨著埋深比C/D增加極限支護壓力σT增加斜率有所增大(見表1);當埋深比C/D相同時,整體破壞所需σT的增加幅度略大于局部破壞情況,同樣是由于兩種破壞模式下的土體松動破壞區域范圍的差異性所致。 圖11 土層容重對極限支護壓力的影響 當γ=20 kN/m3、C=10 kPa、φ=15°時,隧道開挖面極限支護壓力σT隨地面超載壓力σ0的變化關系曲線見圖12。由圖12可知,整體失穩和局部失穩兩種破壞模式下,極限支護壓力σT隨著地面超載σ0的增加均呈線性增加,且其變化幅度與埋深比C/D無關(見表1);相對土層的強度參數和容重,地表超載對隧道開挖面極限支護壓力的影響較小。隧道上覆土層厚度C越大,整體失穩與局部失穩兩種模式下的極限支護壓力σT之間的差值越大。 圖12 地面超載對極限支護壓力的影響 (4)黏聚力、內摩擦角和土層容重影響的比較分析 埋深比C/D=2.0、φ=15°、C=10 kPa時情況下,假定開挖面極限支護壓力σT分別為30、40、50 kPa時,黏聚力c和內摩擦角φ分別隨土層容重γ的變化規律,見圖13。由圖13可知,σT一定時,黏聚力c隨土層容重γ的增加均呈線性增大趨勢;內摩擦角φ同樣隨土層容重γ的增加逐漸增大,且增加的幅度隨γ的增加略有減緩。當γ由15 kN/m3增加到25 kN/m3時,σT分別保持為30、40、50 kPa情況下,c均增加了10 kPa(即,Δc/Δγ=1.0),而φ只是分別增加了5.23、5.65、6.17°(即,Δφ/Δγ=0.523、0.565、0.617)。由上述分析可知,黏聚力c和土層容重γ的變化對σT影響的敏感程度相當;而相對c和γ,內摩擦角φ的變化對σT的影響更為顯著。 圖13 σT為定值時,c、φ隨γ的變化規律 本文針對已有文獻試驗報道的隧道開挖面破壞形態,提出了新的三維破壞模式,利用極限分析上限法得到了黏土地層中隧道三維開挖穩定的極限支護壓力上限解,并與已有計算方法進行了比對,驗證了本文計算方法的合理性和正確性,分析了土體物理參數、地面超載情況等因素的影響,得到如下結論: (1)采用隧道開挖面前方為橢圓對數螺旋體和拱頂上部為半橢圓球體的組合破壞模式,并將橢圓對數螺旋體劃分為多個截橢圓錐體的滑動破壞機制,使得橢圓錐底面的長短軸以及子母線傾角的計算更為簡潔,方便得到每個橢圓錐體的幾何參數,容易推導出開挖面三維破壞極限支護壓力的目標函數,該破壞模式與試驗結果更為接近,符合隧道工程開挖實際情況。 (2)整體失穩情況下,極限支護壓力σT隨著埋深比C/D、土層容重γ、和地面超載σ0的增加均呈現出線性增加的趨勢;而σT隨著黏聚力c和內摩擦角φ增加分別呈線性減小和指數衰減的趨勢,并最終減小為0;黏聚力c和土層容重γ的變化對σT影響的敏感程度相當;而相比c和γ,內摩擦角φ的變化對σT的影響更為顯著。 (3)局部失穩情況下,隧道開挖土體的松動破壞區主要受內摩擦角φ的影響;極限支護壓力σT隨著土重度γ的增加呈線性增加,而σT隨著黏聚力c和內摩擦角φ增加同樣分別呈線性減小和指數衰減的趨勢,并最終減小為0;當埋深比C/D超過一定值時,土體松動區位于上覆土層內部,由于土拱效應,σT為定值不再受上部土層厚度的影響;當內摩擦角φ>30°或<5°時,兩種失穩模式下的極限支護壓力σT差距較小;當5°<φ<30°,兩種失穩模式下的結果差距較大,且埋深比C/D越大,兩種破壞模式下的極限支護壓力差距越大。2.3 絕對速度和相對速度的遞推關系
2.4 隧道掌子面極限支撐力計算
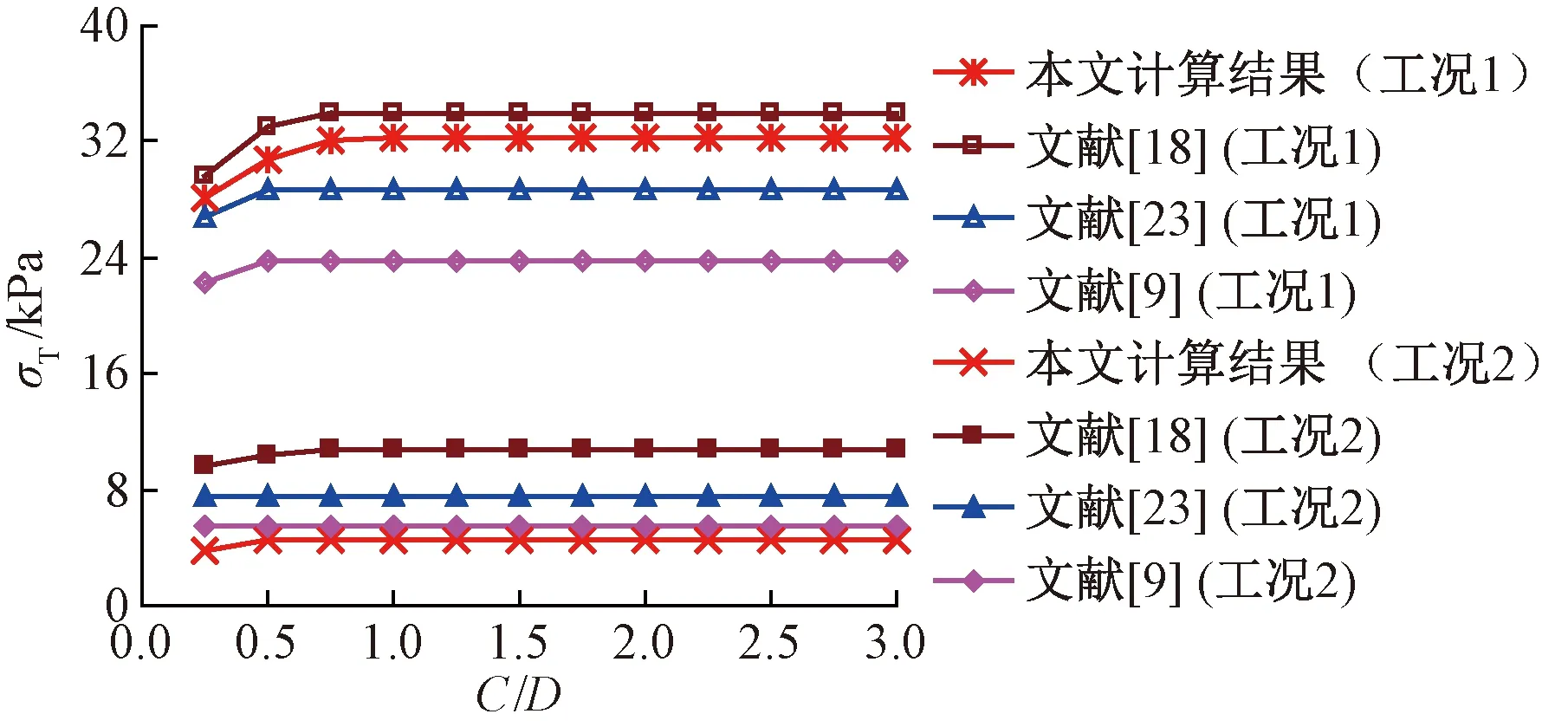
3 計算結果驗證與分析
3.1 本文計算方法驗證
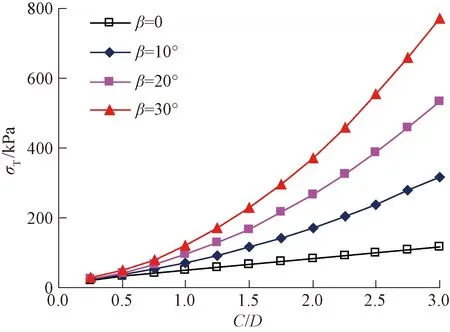
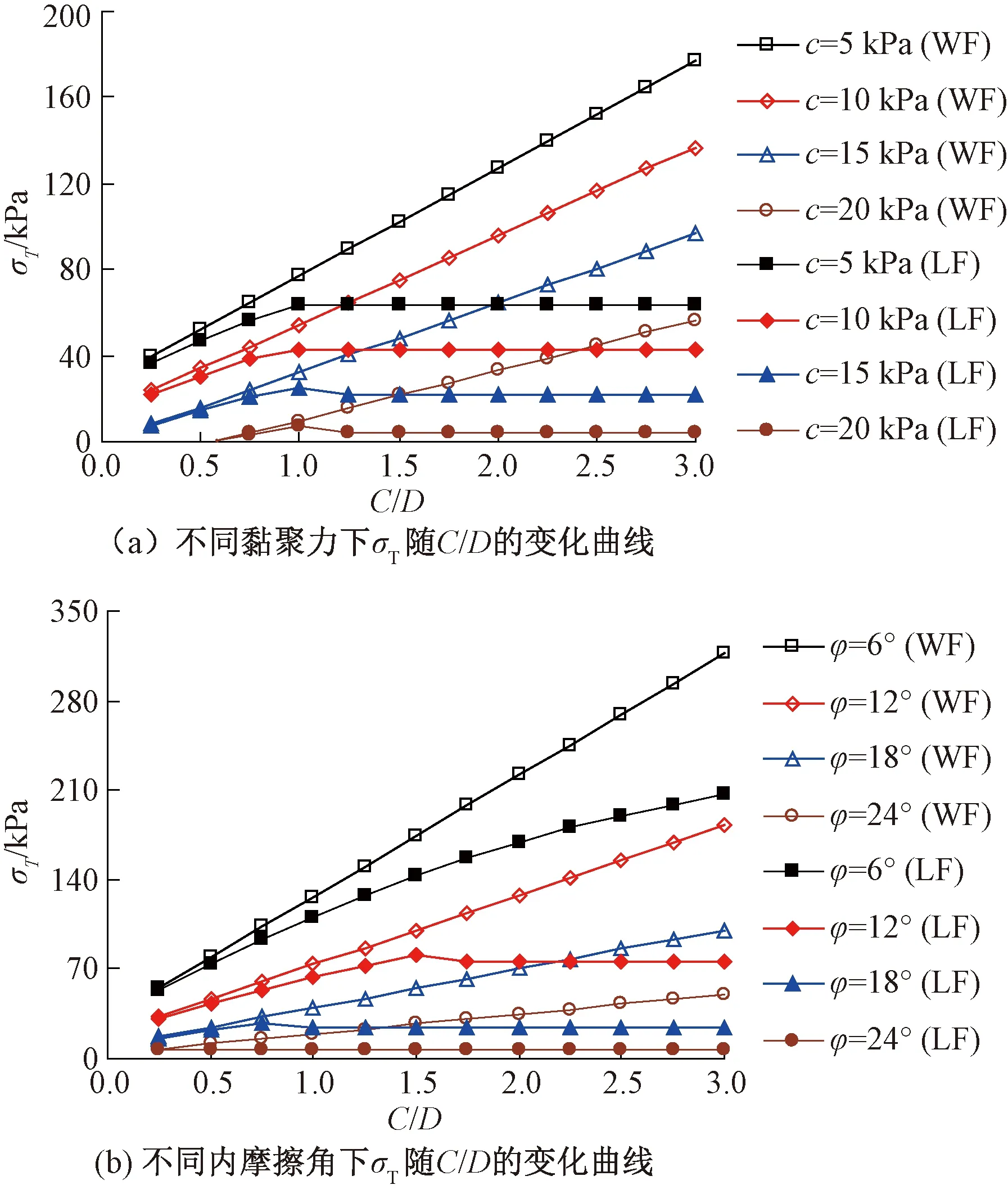
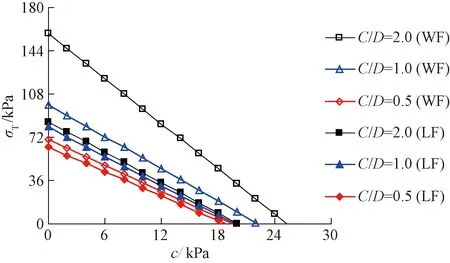
3.2 影響因素分析
4 結論

