基于棧式自編碼神經網絡的腦電信號情緒識別

劉 鵬，喬曉艷

(山西大學 物理電子工程學院，山西 太原 030006)

0 引 言

情緒無時無刻不在影響著人們的工作生活，如果能使計算機具有識別人類情感的功能，將會在醫療、 教育、 養老、 娛樂、 人機交互等多個領域產生巨大的促進作用. 目前，自動情緒識別的研究，包括離散和連續情感模型的生理和非生理信號情緒識別. 連續維度情感模型較離散情感模型而言，可以更加準確地刻畫人的情緒狀態，貼合人的真實感受，成為了各國研究人員在情緒識別方面的追求目標. Koelstra等人[1]在DEAP數據集上提取腦電(EEG)信號δ，θ，α，β節律功率譜特征，使用樸素貝葉斯(NB)分類器在效價、 喚醒度上進行分類，正確率最高分別達到57.6%和62.0%； Li等[2]在DEAP數據集上通過小波尺度變換將多導聯神經生理信號封裝成網格狀幀，結合卷積神經網絡(CNN)和遞歸神經網絡提取任務相關特征，在效價和喚醒度兩個維度上進行情緒識別，算法平均正確率分別為72.1%和74.1%； Liu等[3]在DEAP數據集上提取腦電信號特征，通過組合最大相關性最小冗余和主成分分析融合了高維特征，使用支持向量機(SVM)進行分類，在效價和喚醒度上分類正確率分別為72.4%和76.1%. 闞威等[4]在DEAP數據集上將腦電信號劃分為多個時間段后分別提取其特征，采用長短時記憶(LSTM)算法進行維度情感分類，正確率分別為73.9%和73.5%； 晁浩等[5]先在DEAP數據集中提取腦電信號表征的情感初始特征，通過深度信念網絡(DBN)將初始特征進行高層抽象表示，再利用受限制玻爾茲曼機實現情感分類，在效價和喚醒度二維情感維度上分別得到78.2%和77.1%的正確率.

目前，在腦電生理信號情緒識別中，基于維度情感模型的連續情緒識別正確率普遍不高，無法滿足實際應用需要，而且分類過程中存在情感類別標簽劃分不統一、 情緒生理特征個體差異較大、 提取的與情緒相關的生理信號特征不充分、 差異也不顯著[6]. 因此，本文針對這些問題，在維度情感數據集上，對音樂視頻誘發下的情緒腦電信號進行多角度特征提取、 歸一化腦電處理以及情感標簽分析，在此基礎上設計棧式自編碼深度學習算法實現情緒的有效分類，獲得了較好的識別正確率，為實現生理信號情緒自動分析和識別奠定堅實基礎.

1 維度情感模型

1.1 DEAP數據集

DEAP數據庫[1]是由Koelstra等研究人員開發的開源數據集，主要用于研究生理信息的情緒識別. 它記錄了32名被試觀看音樂視頻時的腦電數據和外圍生理數據，并對音樂視頻在維度空間進行情感標注. 每個被試者分別觀看40個精心挑選的時長60 s的音樂視頻(MV)，每個視頻有對應的維度情感標簽. 同時利用生理測量儀采集記錄被試者的生理數據，每次實驗還記錄了3 s自然狀態下的生理數據，以及被試者根據效價、 喚醒度、 控制度、 相似度對每個視頻的評分. 此外，對于32名被試者中的22名，記錄了觀看音樂視頻時的面部表情. 實驗以512 Hz的采樣率記錄腦電信號，并經過預處理之后降采樣為128 Hz. DEAP數據集中每名被試者的數據內容包含了40個音樂視頻誘發下的40通道生理數據和4個維度的情感標簽數據，如表1 所示.

表1 DEAP數據集內容

本文選取與情緒最相關的左右大腦半球對稱的8個導聯腦電數據進行研究，對應的導聯分別為fp1，fp2，f3，f4，p3，p4，o1，o2.

1.2 情感模型與標簽選取

本文情緒標簽生成基于數據集中測試者對MV的情緒評價. 在生成情緒標簽之前，涉及到如何對情緒進行劃分的問題以及采用何種情感模型的問題. 在DEAP數據集中，被試者對MV的評價是從4個維度來量化情緒的，分別是效價、 喚醒度、 相似度和控制度. 效價和喚醒度是目前大多數研究采用的維度情感模型，效價代表個人的正負性情緒狀態，如高興和不高興. 喚醒度表示情感的強度，如平靜和興奮. 效價、 喚醒度的情感標簽評分范圍均為1～9. 神經生理學研究表明效價和喚醒度可以很好地刻畫人的不同情緒狀態，本文正是基于這兩個維度進行情緒識別研究.

在情緒分類問題中，對情感標簽的劃分是實現情緒分類的前提，由于人不僅有正性與負性情緒，往往還會有介于兩者之間的情感狀態； 在情緒強烈程度上，除了強弱之外還會出現平靜狀態，因此情感識別要充分考慮到情緒的不同狀態. 只有準確標定情緒狀態，在機器分類中才能更準確地識別情緒. 為了探索這種模糊情緒狀態對識別結果的影響，本文對效價和喚醒度分別采用不同的情緒標簽閾值進行維度情緒狀態劃分. 第一類情況： 情緒標簽分值大于7作為高效價高喚醒度，小于3作為低效價低喚醒度； 第二類情況： 情緒標簽分值大于6作為高效價高喚醒度，小于4作為低效價低喚醒度. 通過選取不同標簽閾值，分析情緒的模糊程度對識別結果的影響. 以上兩種不同閾值情況下，DEAP數據集對應于效價和喚醒度情感標簽的樣本數量也不同，如表2 所示.

表2 數據集效價和喚醒度樣本個數

2 腦電特征提取

腦電信號特征主要由時域特征、 頻域特征、 時頻特征及非線性特征構成[7]. 由于情緒腦電信號的復雜性以及腦電個體差異性，對于每個被試者記錄時長為63 s的腦電信號，對應減去前3 s自然狀態的腦電數據，可獲得被試者情緒誘發的腦電信號，并可消除個體差異. 然后，提取情緒腦電信號時域、 頻域、 非線性特征并進行歸一化處理，并進行不同特征組合.

2.1 頻域特征提取

已有研究表明，腦電活動的θ(4 Hz～8 Hz)，α(8 Hz～13 Hz)，β(13 Hz～30 Hz)和γ(30 Hz～45 Hz)節律與人的心理和情緒狀態具有密切關系. 因此提取腦電頻域特征時，先將信號映射到對應頻段上，然后得到各個頻段上的特征量. 由于腦電信號是隨機信號，本文采用AR模型功率譜估計方法進行頻域分析和特征提取. AR模型又稱自回歸滑動平均模型，估計模型參數需要求解Y-W方程[8]. AR模型的系統函數

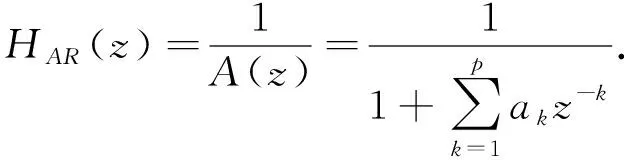
(1)

模型輸出功率譜

(2)

式中：ak是模型參數，P為階數，Burg算法可以快速實現模型參數估計.

采用AR模型方法獲得EEG信號的功率譜，進而計算腦電各個節律對應的譜能量或功率，作為腦電θ，α，β和γ節律的頻域特征.

2.2 時頻特征提取

小波包變換是一種分析非平穩過程的有效方法，提供了更為精細的信號分解，它將頻帶進行多尺度劃分，對多分辨率分析沒有細分的高頻部分以二叉樹方式分解成等頻帶寬的子空間，并根據被分析信號的特征，自適應地選擇相應頻帶，使之與信號頻譜相匹配，從而提高時頻分辨率[9].

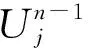
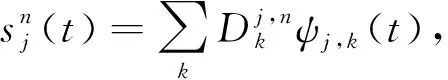
(3)

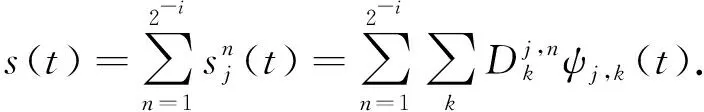
(4)

小波包節點能量可以有效表示信號能量，定義小波包節點能量

(5)

信號總能量可以表示為不同頻帶小波包節點能量之和，即

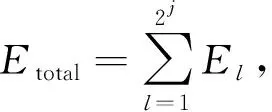
(6)

則小波包能量占比

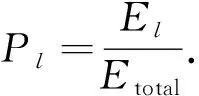
(7)

它反映了腦電各個頻帶對應的小波包能量分布情況.

本文采用db3小波對EEG信號進行了3層小波包分解，重構后提取了8個節點對應的小波包系數均值、 標準差及小波包節點能量占比等時頻特征. 圖1 所示為小波包重構后各節點的EEG信號波形.

圖1 小波包重構后各節點的EEG波形Fig.1 EEG waveform of each node after waveletpacket reconstruction

2.3 非線性特征

樣本熵反映了時間序列的復雜度，能夠衡量時間序列中產生新模式概率的大小，樣本熵值越大，產生新模式的概率越大，序列越復雜. 不同情緒狀態下，對應大腦皮層被激活的程度不同，腦電活動的復雜性也不同. 因此，樣本熵特征可以反映情緒腦電的變化. 樣本熵

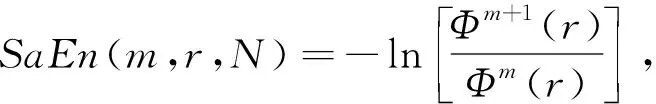
(8)

式中：N為時間序列的長度；r為選定的相似容限值；m為模式維數.Φm+1(r)迭代計算步驟如下[10]：

1) 對一個長度為N的時間序列[x(1),x(2),…,x(N)]，按順序重構m維相空間得到Y(i)=[x(i),x(i+1),…,x(i+m-1)]和Y(j)=[x(j),x(j+1),…,x(j+m-1)]，其中i,j=1,2,N-m+1；

2) 定義Y(i)與Y(j)之間的距離d[Y(i),Y(j)]為兩者對應元素中差值最大的一個，即

d[Y(i),Y(j)]=

(9)

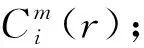
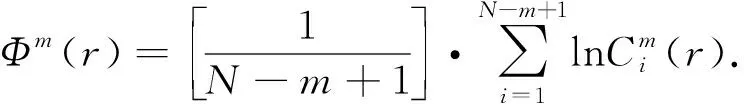
(10)

5) 設定嵌入維數m+1，重復步驟1)～4)，得到Φm+1(r)；

本文選取嵌入維數m為2，閾值距離為0.2倍的信號標準差.

小波包熵反映了隨機序列的不確定性，小波包熵值越大表明序列無序性越強[9]. 腦電信號的小波包熵與情緒狀態密切相關，在不同情緒誘發下，大腦神經元抑制/興奮狀態發生變化，導致腦電序列的無序性隨之發生變化，故可提取腦電的小波包熵進行情緒識別，小波包熵

WEP=-∑Plln[Pl],

(11)

式中：Pl為式(7)所提取的小波包能量占比.

綜上所述，本文提取情緒腦電信號頻域、 時頻域和非線性共30個特征，如表3 所示. 對這些特征進行不同組合，構成對應特征向量，可以研究多特征融合對腦電情緒識別的影響.

表3 提取的情緒腦電特征

3 棧式自編碼的維度情緒識別

棧式自編碼神經網絡算法是一種半監督的深度學習算法. 它借鑒大腦神經元興奮性機制，利用稀疏自編碼器對數據逐層預訓練，獲得網絡初始權值和閾值，然后通過多層神經網絡反向傳播調節優化整個網絡權值. 稀疏性減少了實際計算量，自編碼優化了初始權值，因此算法具有收斂速度快、 不易陷入局部極小的優點. 此外，深層的棧式自編碼算法還具有自動訓練優化特征的優點. 棧式自編碼神經網絡由稀疏自編碼器和softmax分類器構成，結構如圖2 所示.

稀疏自編碼器由輸入層、 隱層、 輸出層組成多層深度神經網絡，采用逐層貪婪訓練方法使自編碼器的輸出值無限趨近于輸入值[11]. 訓練稀疏自編碼器的代價函數為

Jsparse(W,b)=‖hw(X)-X‖2+β∑|hj|,

(12)

式中：β控制稀疏性懲罰因子的權重； 第一項為輸出值與輸入值的二范數，使輸出結果與輸入逼近； 第二項為隱藏層神經元激活輸出的一范數，作為稀疏自編碼器的稀疏性限制. 將訓練好的稀疏自編碼器連接softmax回歸模型，通過反向傳播算法從Softmax輸出層到隱層逐層對代價函數求偏導，微調各層權值向量，對整個網絡進行迭代優化，分類器計算對應標簽的概率P(j|H(2))并輸出分類結果.

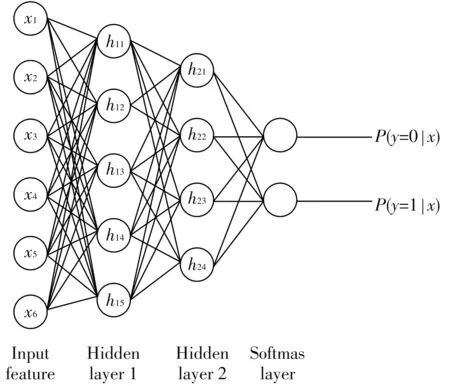
圖2 棧式自編碼算法結構圖Fig.2 Structure diagram of stack auto-encoder algorithm

本文棧式自編碼神經網絡的輸入層節點為腦電特征向量，輸出層節點數為2，即維度情緒狀態. 通過仿真試驗，選擇了兩個隱含層，第一隱層節點數為15，第二隱層節點數為7. 網絡訓練樣本和測試樣本按照4∶1分成訓練集和測試集. 圖3 為網絡訓練的單次學習曲線(鋸齒狀)和平均學習曲線(線狀). 從中可以看出，網絡訓練在開始迭代時震蕩較大，當迭代達到600次時誤差目標函數下降到0.001，網絡參數訓練達到最佳. 將訓練好的棧式自編碼網絡利用測試集樣本進行分類測試，可獲得情緒識別正確率

(13)

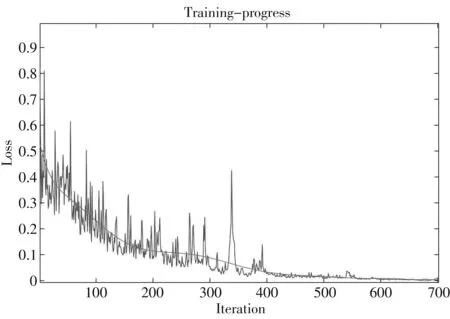
圖3 棧式自編碼算法學習曲線Fig.3 Learning curve of stack auto-encoder algorithm

此外，引入正類、 負類樣本的召回率RT,RN作為評價指標，計算公式為

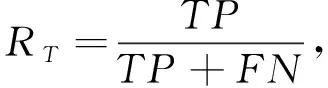
(14)

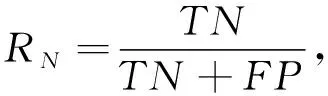
(15)

式中：TP，TN分別表示被正確分為正類或負類的樣本個數；FP，FN表示被錯誤分為正類或負類的樣本個數. 本文計算識別正確率時，將網絡輸出高效價、 高喚醒度的樣本記為正類樣本，輸出低效價、 低喚醒度的樣本記為負類樣本.

將本文提取的情緒腦電特征，應用棧式自編碼算法進行維度情緒識別，并與使用DEAP數據集的其它方法進行對比，如表4 所示. 從表4 中可以看出，無論是效價情緒維度還是喚醒度情緒維度，本文采用的棧式自編碼算法對維度情緒識別的正確率均高于其他3種方法，表明了該算法應用于腦電情緒識別的有效性.

表4 不同分類方法結果對比

4 結果與分析

本文主要從3個方面進行仿真分析： ① 樣本數據均衡對情緒識別結果的影響; ② 腦電特征對情緒分類的影響; ③ 情感標簽劃分對識別結果的影響.

4.1 樣本數據均衡對情緒識別的影響

由表2 中可以看出，無論是在效價還是喚醒度維度上，用于分類識別的數據樣本量相差較大. 為了探究這種數據不均衡對算法分類結果的影響，本文設計了兩種方式下的情緒分類，第一種方式是不對樣本數量進行處理，將所有樣本數據按照4∶1 劃分為訓練集和測試集進行訓練和測試； 第二種方式是對數據進行均衡處理，即在每個情感維度上(效價、 喚醒度)選取的樣本數據基本平衡，即維度情緒標簽數量相等. 具體做法是： 按照樣本數量少的那個，選取對應維度的樣本數量，之后再按照 4∶1 劃分為訓練集和測試集. 按照式(13)～式(15)計算正確率及兩類樣本召回率，仿真結果如表5 所示.

表5 數據均衡與數據未均衡識別結果對比

表5 結果顯示，數據樣本均衡或者不均衡，效價維度情緒的識別正確率相差不大，均在80%左右，喚醒度維度情緒識別正確率相差4.5%. 但是考察兩類樣本召回率時，可以發現數據不均衡時，低效價情緒召回率為92.2%，高效價召回率為60.3%，其結果相差很大，同樣，低喚醒度情緒召回率為84.5%，高喚醒度召回率為60.0%，這是由于數據樣本不平衡導致的. 數據均衡后，不同維度情緒狀態的識別正確率大體相同. 綜上可知，在腦電情緒識別中，有必要對樣本數量進行均衡化處理，可以提高算法的穩健性.

4.2 不同特征組合對分類結果的影響

本文從頻域、 時頻域和非線性多個維度提取了情緒腦電特征，為了驗證特征的有效性并獲得最佳化的特征，選用不同腦電特征組合，經過數據均衡化處理后，研究對分類正確率的影響，如表6 所示.

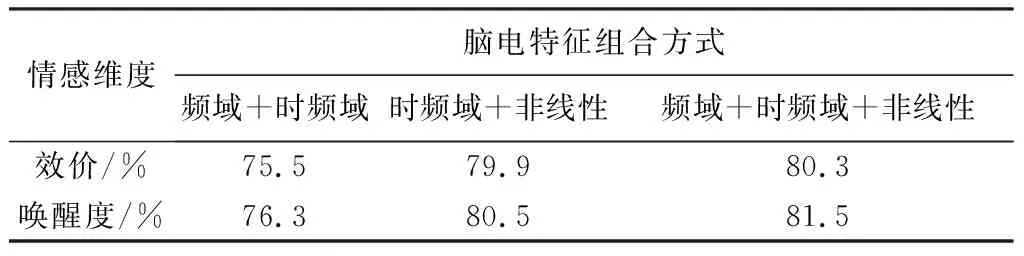
表6 不同特征組合結果對比

表6 結果顯示，在喚醒度及效價維度上，3種特征組合用來分類情緒的正確率相比頻域和時頻域特征組合平均高出6%左右，比時頻域和非線性特征組合平均高出3%左右. 由此可以得出結論： 選用頻域、 時頻域、 非線性3種特征組合可以更好地表征不同情感狀態，情緒識別正確率更高，因此盡可能提取情緒腦電多種特征，可以更充分挖掘腦電信號中蘊含的情緒信息.

4.3 情感標簽閾值對分類結果的影響

將效價和喚醒度兩個情緒維度上的數值按照不同閾值設定，劃分為兩大類. 第一類閾值設定效價值小于3為低效價，大于7為高效價； 第二類閾值設定效價值小于4為低效價，大于6為高效價. 喚醒度也采取同樣方法設定情感標簽閾值. 經過數據均衡化處理，選用3種組合特征進行情緒分類，分類正確率結果如表7 所示.

表7 不同情感標簽閾值分類正確率對比

表7 結果顯示，無論是效價還是喚醒度，第一類閾值設定的情緒識別正確率均大于第二類閾值設定. 原因在于第一類閾值的情緒狀態，無論是喚醒度還是效價，情緒表現更加強烈和明確，因而更有利于機器識別； 第二類閾值的情緒狀態更加模糊化，因而較難以識別. 由此表明，在對情緒進行維度標簽時，閾值設定合適有助于提高情緒識別正確率.

5 結束語

本文基于DEAP數據集對EEG信號進行了頻域、 時頻域和非線性特征提取，并利用棧式自編碼算法在效價及喚醒度兩個維度對情緒進行分類識別. 與其他方法相比，取得了更高的識別正確率，表明棧式自編碼深度學習算法對EEG情緒識別的有效性. 仿真結果表明： 對數據進行均衡化處理，算法更加穩健； 多維特征進行融合，情緒識別正確率更高； 情感標簽的閾值設定對情緒識別結果會產生影響. 該研究可以應用于醫療、 教育、 人機交互等領域的腦電情緒識別.