一種降低BICM-ID系統誤比特率的高階APSK星座映射方法
付 芳,焦 琦,張志才
(山西大學 物理電子工程學院,山西 太原 030006)
0 引 言
高階振幅移相鍵控(Amplitude Phase Shift Keying, APSK)調制具有速率快、 頻譜效率高和信號幅度起伏小等特點,適合應用于衛星通信領域,但存在誤比特率高的問題. 為了降低系統誤比特率,可將高階APSK調制與比特交織編碼調制迭代譯碼(Bit Interleave Coded Modulation-Iterative Decoding, BICM-ID)系統相結合,發端采用更接近香農極限的低密度奇偶校驗碼(Low Density Parity Code, LDPC)作為信道編碼方法,收端采用軟解調軟譯碼聯合迭代方法[1].
針對聯合編碼調制系統的星座映射,文獻[2]提出了一種預編碼方法,該方法以格雷映射作為中間映射,優點是不僅簡單易實現,而且能降低地板效應,缺點是誤比特率非常高; 文獻[3]提出了一種二進制交換算法,計算復雜度高不適用于高階映射; 文獻[4]提出了一種尋找最優映射的RTS方法,該方法能夠降低聯合卷積碼的BICM-ID系統在高信噪比時的錯誤平層,但是由于該方法基于計算復雜的二次分配問題,當應用于優化高階星座時,計算量龐大; 文獻[5]對衛星數字化視頻廣播第二代DVB-S2標準中的(4,12)-16APSK映射方法[6]提出了備選方法,簡單記作(6,10)-16APSK星座映射方法,其內環分布6個星座點,外環分布10個星座點,誤比特率性能略優于DVB-S2標準中的方案.
蝙蝠算法最初由文獻[7]于2010年提出,文獻[8]在2015年提出了一種新型蝙蝠算法,嵌入了自適應局部搜索策略,增強了種群的多樣性,文獻[9]在2019年基于多子種群理論對蝙蝠算法做了改進. 到目前為止,蝙蝠算法都只用于解決控制領域中的優化問題,本文首次將蝙蝠算法用于通信領域的星座映射方面,利用文獻[8]所提蝙蝠算法對高階APSK調制的星座映射進行優化設計,旨在進一步降低BICM-ID系統的誤比特率,并從理論和實驗仿真兩方面驗證它的誤比特率性能優于現有映射方法.
1 LDPC-BICM-ID系統模型
在如圖1 所示的聯合編碼調制系統模型中,隨機生成一長串二進制數作為信源發出的信號. 發射端首先采用LDPC編碼器對信源發出的信號進行編碼,編碼后信號再經過比特交織器增大碼字間的歐式距離. 對交織后信號的二進制比特信號進行高階APSK調制,每個比特信號映射到高階APSK星座圖中的一個星座點,其中M表示階數. 調制后的信號通過高斯白噪聲信道傳輸到接收端.
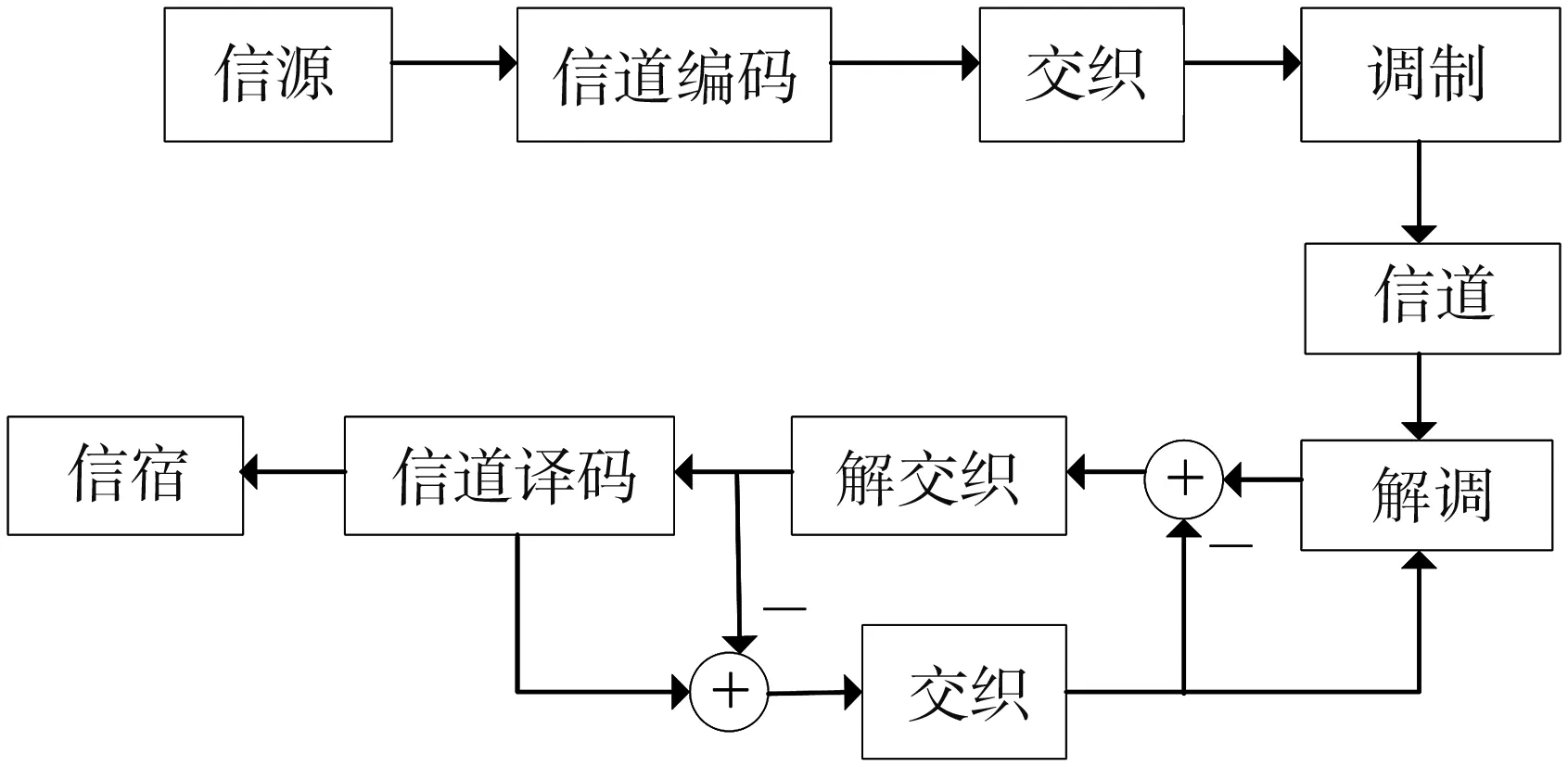
圖1 系統模型Fig.1 System model
在接收端,解調器、 解交織器、 信道譯碼和交織器組成一個軟解調軟譯碼聯合迭代模塊. 解調器的輸入有兩個: 分別是通過無線信道接收到的信號和交織器輸出的各個比特的先驗信息. 用解調器的輸出減去交織器的輸出,相減結果再經過解交織之后變成信道譯碼器的先驗信息. 用譯碼器的輸出減去它的輸入,相減結果再經過交織后作為解調器的先驗信息,如此完成一次軟解調軟譯碼聯合迭代. 最后將聯合迭代結束后的信號送到信宿[9].
2 星座映射
圖2 所示為采用不同映射方法得到的16APSK的星座圖,包括DVB-S2標準中的方法、 預編碼方法、 (6,10)-16APSK星座映射方法,以及通過蝙蝠算法對(6-10)-16APSK進行優化的方法.
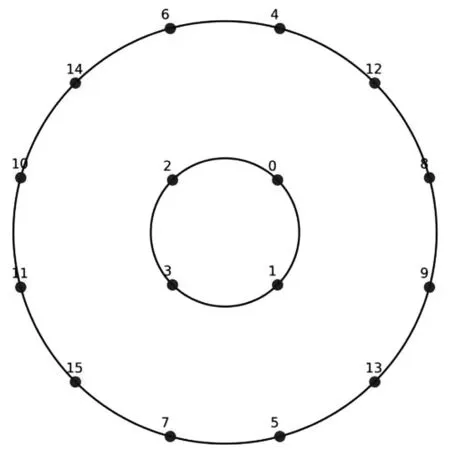
(a) DVB-S2標準中的方法 (b) 預編碼方法
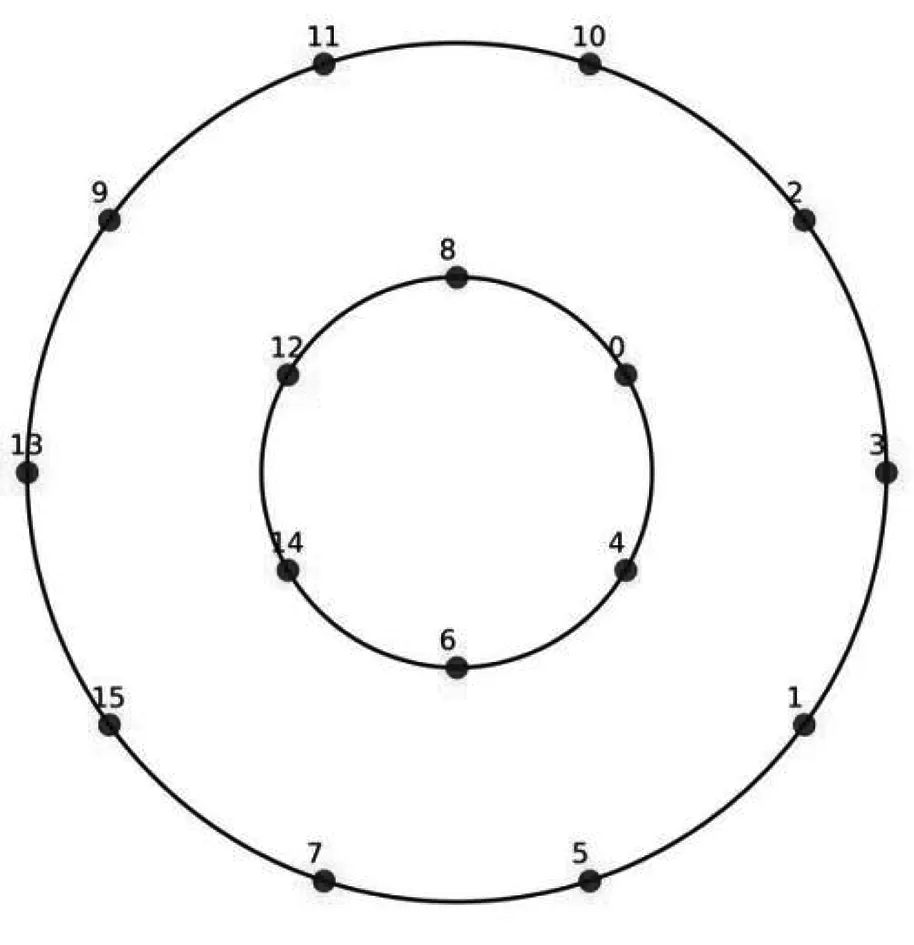
(c)(6,10)-16APSK映射方法 (d) 蝙蝠算法優化后的16APSK圖2 16APSK星座映射圖Fig.2 Constellation map of 16APSK
從圖2 可以看出,預編碼方法和DVB-S2標準中的方法都是由內環4個點和外環12個點組成,(6,10)-16APSK以及用蝙蝠算法優化后的星座圖都是由內環6個點和外環10個點組成. 圖2(d)所示內外環的星座點相位不同,可以理解為將圖2(c)星座圖中的點沿著對應的環進行順時針旋轉和相位偏移,同時改變了內外環的相對半徑比,其數值從圖2(c)的2.20到圖2(d)的 2.265 1.
參數表示星座圖中兩個相鄰星座點之間的不同比特的平均數,理論上該參數越接近1.0,誤比特率性能越好. 如表1 所示,對于16APSK和32APSK星座映射,采用本文所提的方法優化后該參數值都達到理想值1.0,優于現有的預編碼方法和DVB-S2標準中的方法,能夠有效降低聯合編碼調制系統的誤比特率.
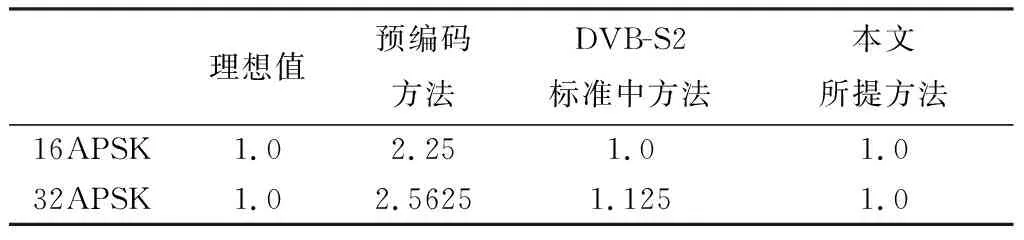
表1 星座映射的參數
蝙蝠算法的優化過程具體包括以下步驟:
步驟1: 初始化種群和參數. 隨機產生D維搜索空間的N個解,其中D是解空間的維數,N是解的個數,每一個解用xij表示,i∈[1,2,…,N],j∈[1,2,…,D],其中i是第幾個解的序號下腳標,j是解空間第幾個維數的序號下腳標,xij由相對半徑比和每個星座點的相位值組成,xij由式(1)得到
xij=xjmin+(xjmax-xjmin)*rand(0,1),
(1)
式中:rand(0,1)是服從均勻分布的隨機數;xjmax和xjmin分別表示搜索空間中第j個值的上下界,由具體的搜索目標決定,這一步驟會產生多個解.
步驟2: 將步驟1產生的多個解中的每一個解xij代入式(2),得到誤比特率
(2)
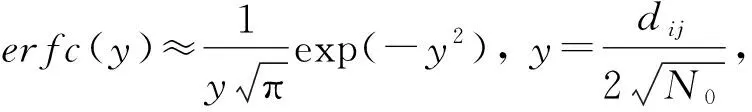
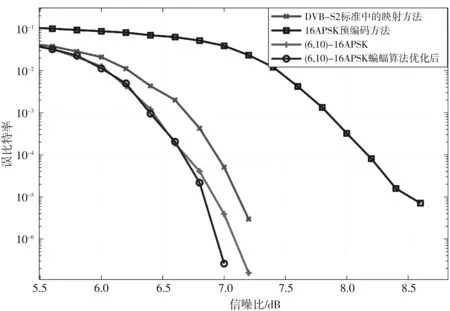
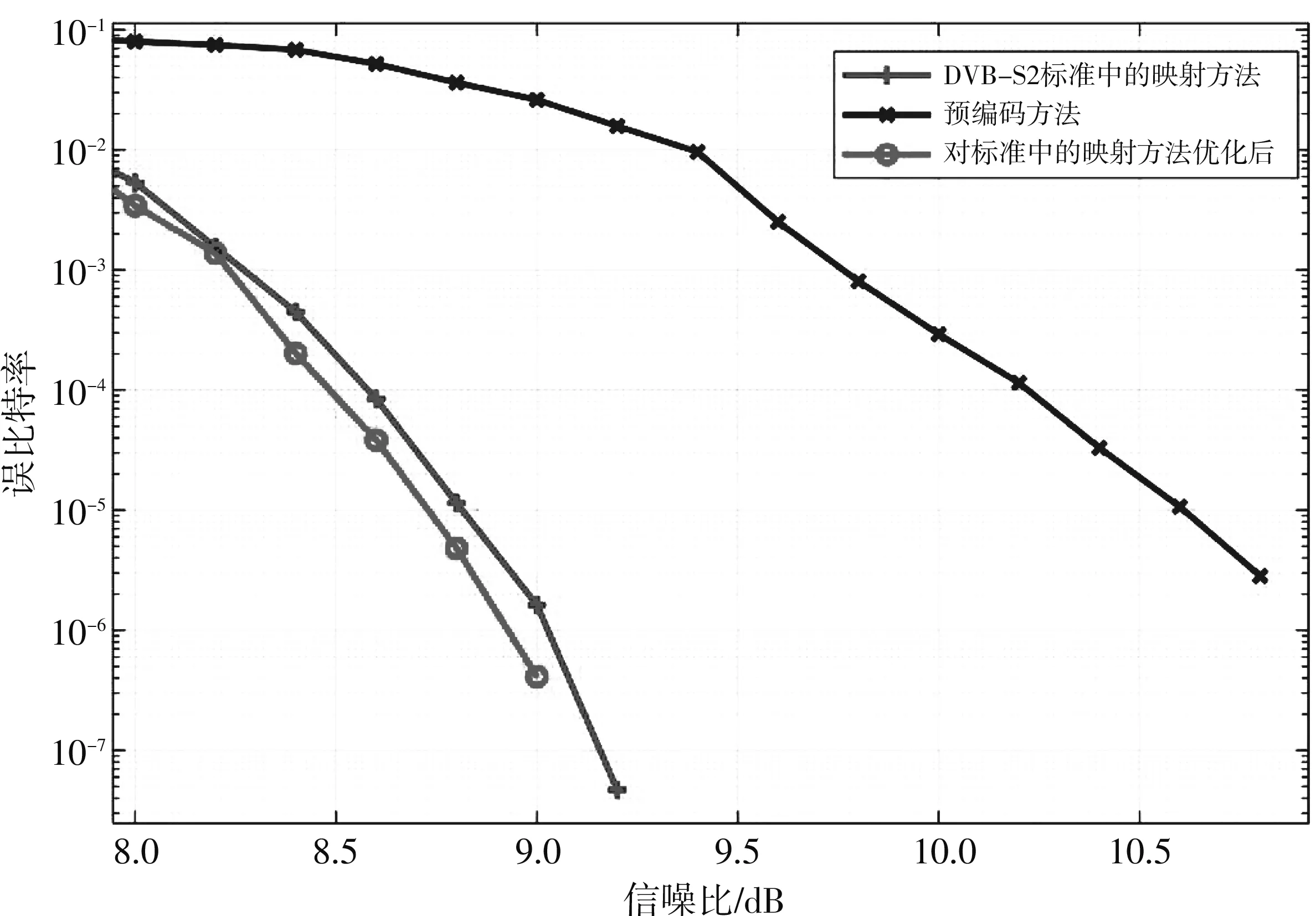
步驟3: 開始迭代,產生新解xij,隨機生成一個0到1之間的隨機數,用rand(0,1)表示,如果rand(0,1) (3) 如果rand(0,1)≥P,更新方法為 fij=fmin+(fmax-fmin)*rand(0,1), (4) (5) (6) (7) (8) (9) 更新脈沖發射率,將脈沖發射率代入式(10)進行更新 (10) 步驟7: 返回步驟3繼續迭代直到達到最大迭代次數,輸出更新后的全局最優解. 通過上述步驟可以看出,全局最優解的搜索過程簡單,嵌入自適應局部搜索策略,在全局最優解周圍利用隨機飛行產生局部新解,然后比較所有解的誤比特率值大小,選擇最小者對應的解,這樣大大降低了全局最優解的搜索時間. 此外,解的更新方法計算復雜度低,要實現解的更新只需更新響度和脈沖發射率兩個參數,不需要調整過多參數,對高階APSK星座映射這類高維度而且復雜的優化問題進行了參數和步驟的簡化. 實驗仿真具體設置為: 信道編碼使用碼長2 304,碼率5/6的LDPC碼; 交織器為隨機交織; 信道模型為高斯白噪聲信道; LDPC譯碼器為LLR-BP譯碼算法; 軟解調器為MAX-log-Map譯碼算法; 軟解調軟譯碼聯合迭代次數設置為4次; LDPC碼譯碼內部迭代次數設置為10次. 星座映射中用到的蝙蝠算法的參數設置為: 最大迭代次數設為800; 種群大小設為50; 脈沖發射率設為0~1; 頻率設為0~1.5; 響度設為1~2; 棲息地選擇概率設為0.6~0.9; 多普勒補償率設為0.1~0.9; 慣性權重設為0.5~0.9; 收縮膨脹系數設為0.5~1. 圖3 為根據圖1 所示系統模型對16APSK多種星座映射方法的誤比特率曲線對比,其中“(6,10)-16APSK蝙蝠算法優化后”為本文所提的星座映射方法. 從圖3 可以看出,當信噪比Eb/N0為7 dB時,采用本文所提方法得到的誤比特率是10-7為最佳,(6,10)-16APSK方法的結果是10-6,DVB-S2標準的結果是10-5,采用預編碼方法的結果是10-2. 圖3 不同16APSK星座映射方法的誤比特率性能對比Fig.3 The BER performance of different 16APSK constellationmapping methods 圖4 為根據圖1所示系統模型對32APSK多種星座映射方法的誤比特率曲線對比,其中“對標準中的映射方法優化后”為本文所提的星座映射方法,基于蝙蝠算法對DVB-S2標準中的32APSK星座映射方法進行了優化. 從圖4 可以看出,當系統的誤比特率為10-5時,采用本文所提方法需要的信噪比為8.73 dB,DVB-S2標準中方法需要的信噪比為8.82 dB,采用預編碼方法需要的信噪比為10.61 dB. 圖4 不同32APSK星座映射方法的誤比特率性能對比Fig.4 The BER performance of different 32APSK constellationmapping methods 本文采用蝙蝠算法對高階APSK星座映射進行優化,以最小化誤比特率作為其優化目標,本文所提方法具有以下特點: 1) 星座映射效率高,全局最優解的搜索過程簡單; 2) 誤比特率性能優于現有的預編碼方法和DVB-S2標準中的星座映射方法; 3) 該星座映射方法僅適用于16APSK和32APSK的優化,不適用于更高階的情況.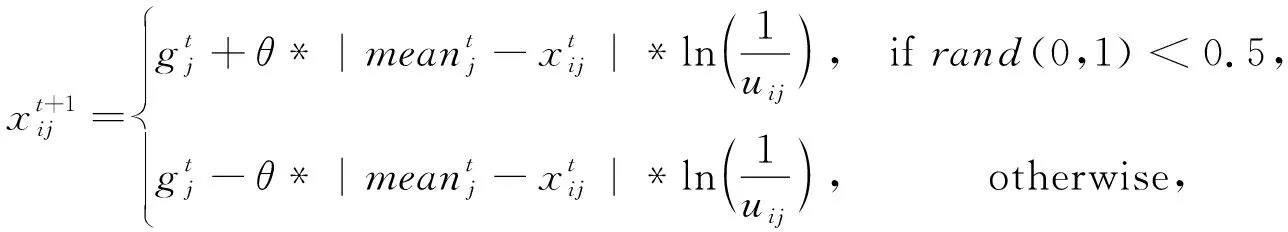
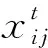
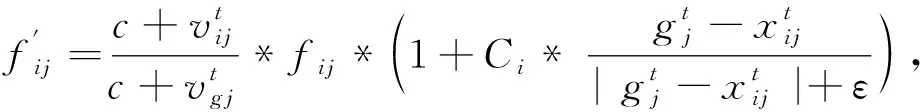
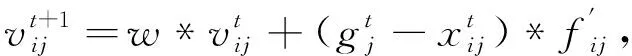
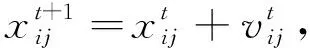
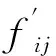
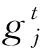
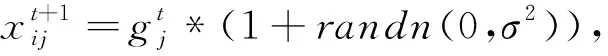
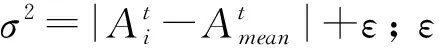
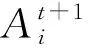
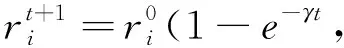
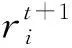
3 實驗結果分析
4 結 論

