鐵路重力式橋墩抗震計算簡化模型研究

魯錦華，陳興沖，丁明波，馬華軍，張熙胤

(蘭州交通大學 土木工程學院，蘭州 730070)

鐵路重力式橋墩因配筋率較低其破壞特征不同于普通鋼筋混凝土橋墩。鞠彥忠等[1-2]對配筋率為0.1%和0.2%的鐵路重力式橋墩進行的擬靜力試驗研究中發現橋墩破壞時混凝土壓碎不明顯，且僅在墩底產生一條或多條裂縫。蔣麗忠等[3]對高速鐵路重力式橋墩的研究中也發現橋墩破壞時墩底未形成明顯的塑性鉸區。Chen等[4-5]對鐵路重力式矩形截面橋墩的研究中發現配筋率為0.1%的橋墩破壞時僅在墩底產生一條裂縫。以上研究發現鐵路重力式橋墩破壞時墩底未形成明顯的塑性鉸區，且破壞部位主要集中在墩底，明顯區別于鋼筋混凝土橋墩的延性破壞特征。作者在前期研究中對配筋率為0.2%的鐵路重力式橋墩進行了擬靜力試驗和振動臺試驗發現僅在墩底形成一條主裂縫，且在動力作用下有明顯的搖擺現象[6]。

針對破壞部位主要集中在墩底，且未形成塑性鉸區的鐵路重力式橋墩，目前主要采用實體單元模型或者纖維單元模型進行分析。劉浩[7]采用ANSYS軟件建立了鐵路重力式橋墩的抗震分析模型，并對其抗震性能進行了分析。邵光強等[8-9]采用纖維單元模型對高速鐵路重力式橋墩進行了分析。研究發現實體單元和纖維單元可以有效模擬鐵路重力式橋墩的抗震性能，但是建模過程繁瑣，計算效率較低，時間成本較高。

依據低配筋鐵路重力式橋墩在墩底僅形成一條主裂縫，且在動力作用下有明顯的搖擺現象，發現該類橋墩具有墩底自由搖擺橋墩的特征。而目前國內外對于搖擺橋墩的抗震分析模型研究較為成熟[10-14]。夏修身[15]對于自由搖擺橋墩提出了簡化的雙彈簧模型；賈登峰[16]提出了設置限位鋼筋的基底隔離橋墩計算分析模型，在自由搖擺模型的基礎上，設置只受拉的桿單元模型纖維鋼筋；馬華軍[17]針對設置限位鋼筋的基底隔離橋墩的計算分析模型進行了簡化，將桿單元簡化為只受拉的非線性彈簧。參考現有搖擺橋墩的抗震分析計算模型，本文提出了一種適用于低配筋鐵路重力式橋墩的簡化的四彈簧模型，用于鐵路重力式橋墩的簡化抗震分析。

1 簡化的抗震分析模型

依據低配筋鐵路重力式橋墩在靜力作用下的破壞特征及在地震作用下的搖擺特征，參考自由搖擺橋墩的雙彈簧模型，考慮縱向鋼筋的約束作用，提出適用于鐵路重力式橋墩的簡化的四彈簧抗震分析模型。

自由搖擺橋墩雙彈簧模型中墩身采用彈性梁單元模擬，橋跨質量簡化為墩頂集中質量，墩底剛臂單元模擬墩身受力方向截面寬度，只受壓的彈簧模擬自由搖擺時橋墩的提離，計算模型如圖1所示。受壓彈簧的剛度k按式(1)、(2)及(3)近似計算。

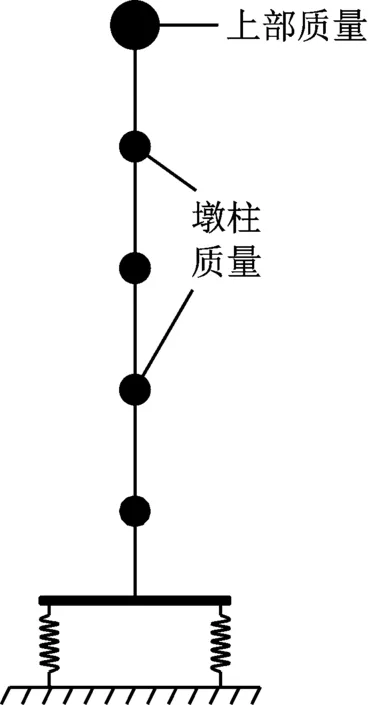
圖1 自由搖擺橋墩兩彈簧模型Fig.1 Two-spring model of free-rocking piers

(1)

(2)

(3)

式中:Kv為豎向剛度；R0為等效半徑；A0為墩底擴大基礎的截面積；G為墩底材料的剪切模量；ν為墩底材料的泊松比。

在自由搖擺橋墩雙彈簧模型的基礎上，再考慮墩身縱向鋼筋的受拉作用，采用非線性彈簧模擬只考慮受拉不考慮受壓的縱向鋼筋，受拉彈簧屈服前剛度按式(4)計算。綜上分析，得到適用于鐵路重力式橋墩的四彈簧計算模型如圖2所示。

(4)

式中:kx為鋼筋屈服前剛度；E為縱向鋼筋的彈性模量；As為參與計算的縱向鋼筋的總面積；Ld為縱向鋼筋計算長度。

圖2中，Fy為縱向鋼筋的屈服力；a點對應縱向鋼筋屈服點；Δy為屈服位移。縱向鋼筋受拉單元的滯回規則為：①→②為加載路徑，③為卸載路徑；④→⑤為再加載路徑。

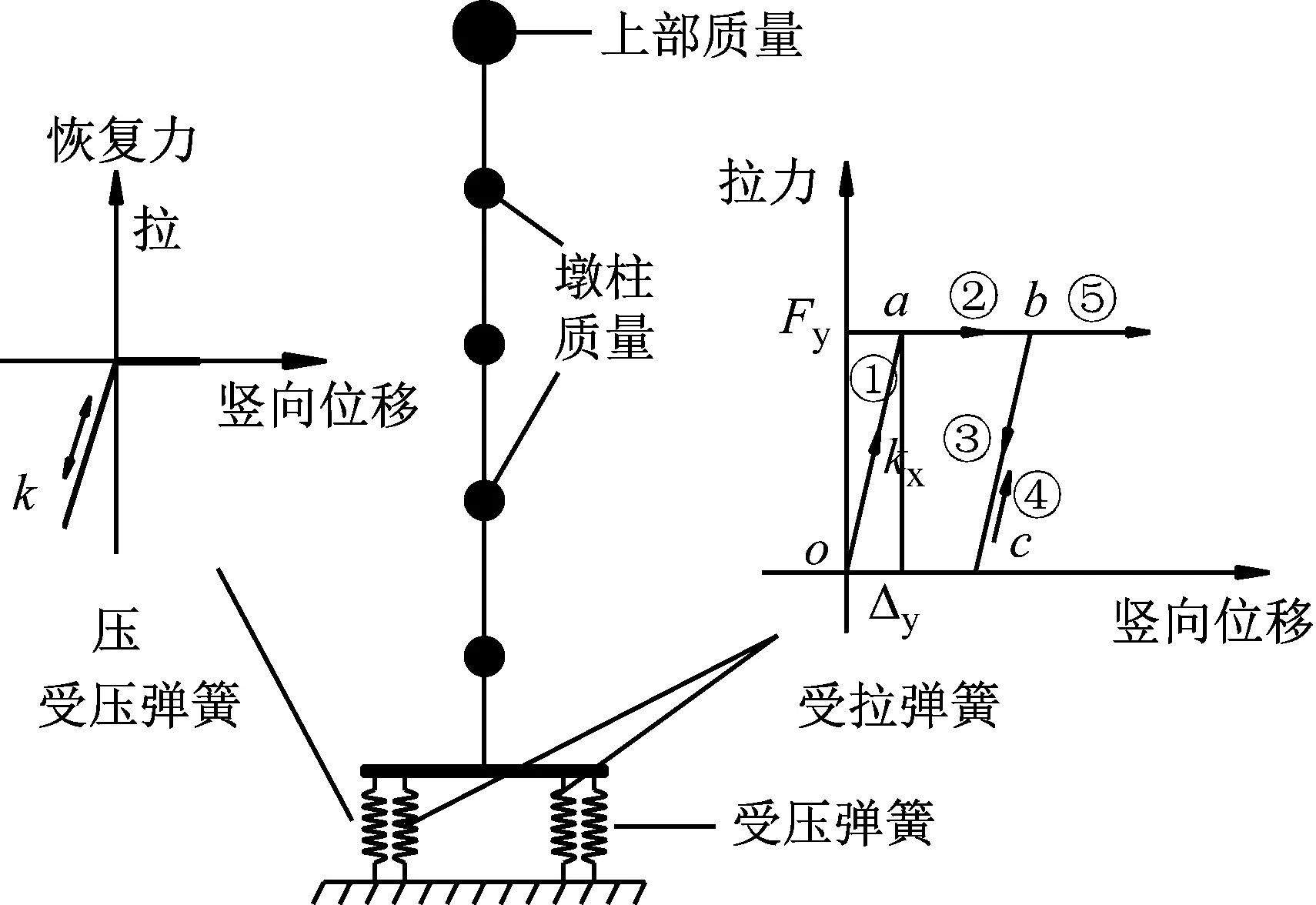
圖2 四彈簧抗震分析模型Fig.2 The four-spring seismic analysis model

文獻[17]針對墩底搖擺橋墩采用四彈簧模型分析了限位鋼筋對自由搖擺橋墩的影響，而本文主要是針對低配筋鐵路重力式橋墩進行的抗震簡化分析，二者研究對象不同，且參數取值也不同。文獻[17]中限位鋼筋僅配置單根鋼筋，且計算受拉彈簧的剛度時，鋼筋取實際鋼筋長度。本文提出的四彈簧模型，鋼筋配置在墩身四周，計算受拉彈簧鋼筋時，鋼筋面積取值為受拉區縱向鋼筋面積之和，且鋼筋計算長度依據文獻[6]中模型橋墩試驗數據進行確定，配筋率為0.2%的橋墩應變測點及鋼筋應變如圖3所示。研究發現隨著位置的增加，鋼筋的應變逐漸減小，距離墩底10 cm時，高度約為等效塑性鉸長度(15.9 cm)的2/3倍，最大應變為鋼筋為514 με，為屈服應變的1/3左右；距離墩底20 cm時，高度約為等效塑性鉸長度的5/4倍，鋼筋應變僅為139 με，遠遠小于鋼筋的屈服應變，該處的鋼筋幾乎不受力，計算時該處以上的鋼筋長度可以不予考慮。結合試驗數據，最終四彈簧抗震分析模型中鋼筋計算高度Ld可按等效塑性鉸長度取值，且物理意義明確，同時下文的計算結果與試驗值的比較也證明了鋼筋計算高度Ld按等效塑性鉸長度取值的可行性。

2 模型驗證

為了驗證簡化的四彈簧模型，采用文獻[6]中的試驗模型橋墩進行對比，墩高為125 cm，截面尺寸為36×25 cm，剪跨比為5.0，軸壓比為4%，各模型橋墩的設計參數如表1所示。

表1 模型橋墩設計參數Tab.1 Design parameters of model piers

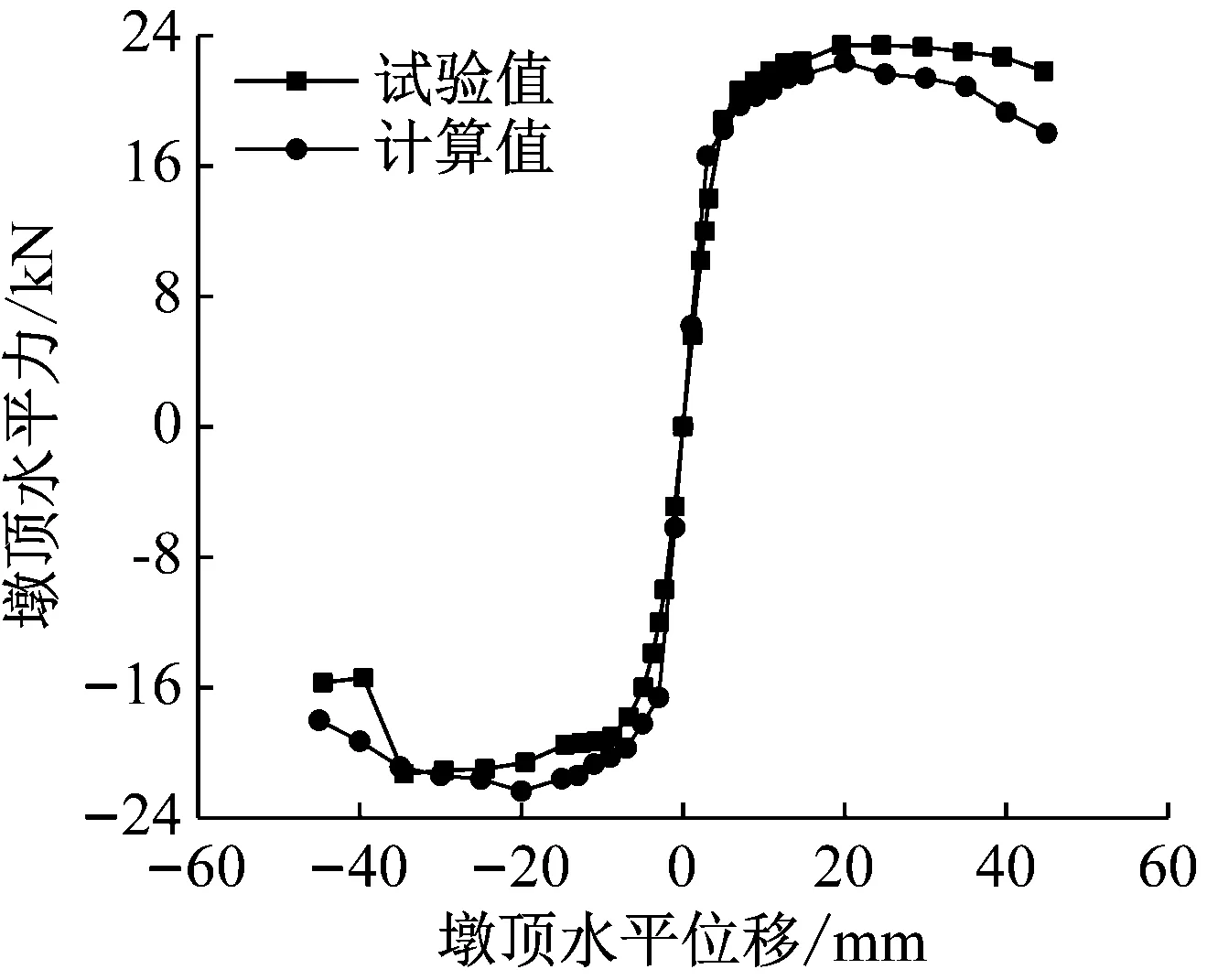
采用四彈簧抗震分析模型對橋墩進行計算分析，得到模型橋墩的滯回曲線與骨架曲線，并與試驗值進行比較，如圖4和圖5所示。

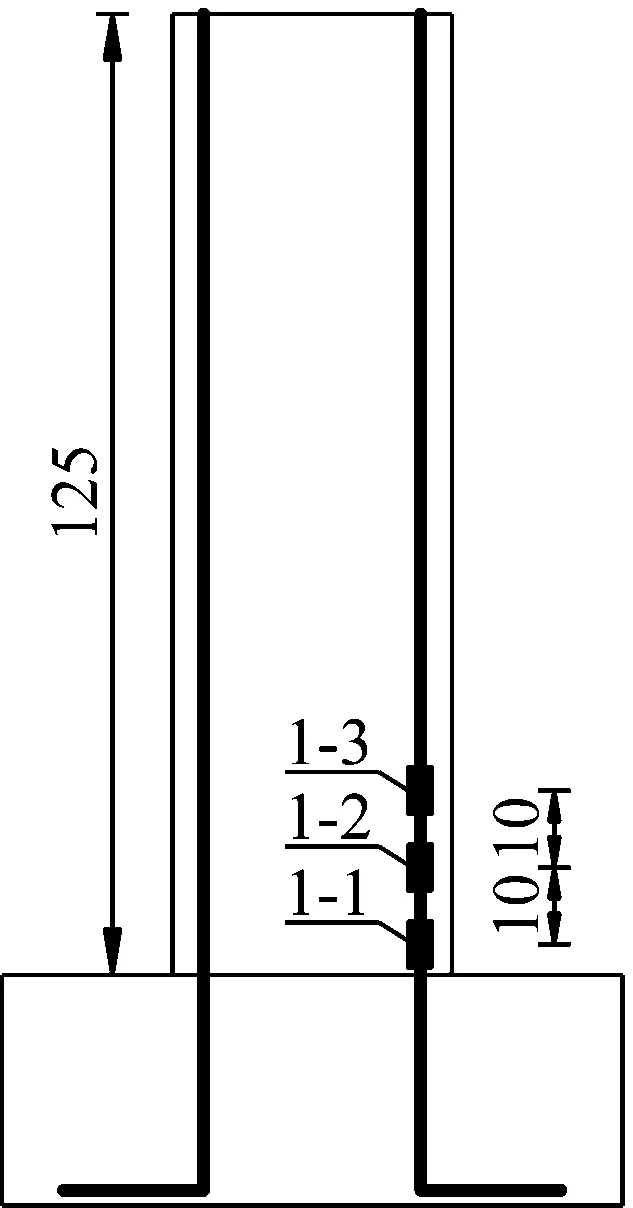
(a) 墩身應變測點

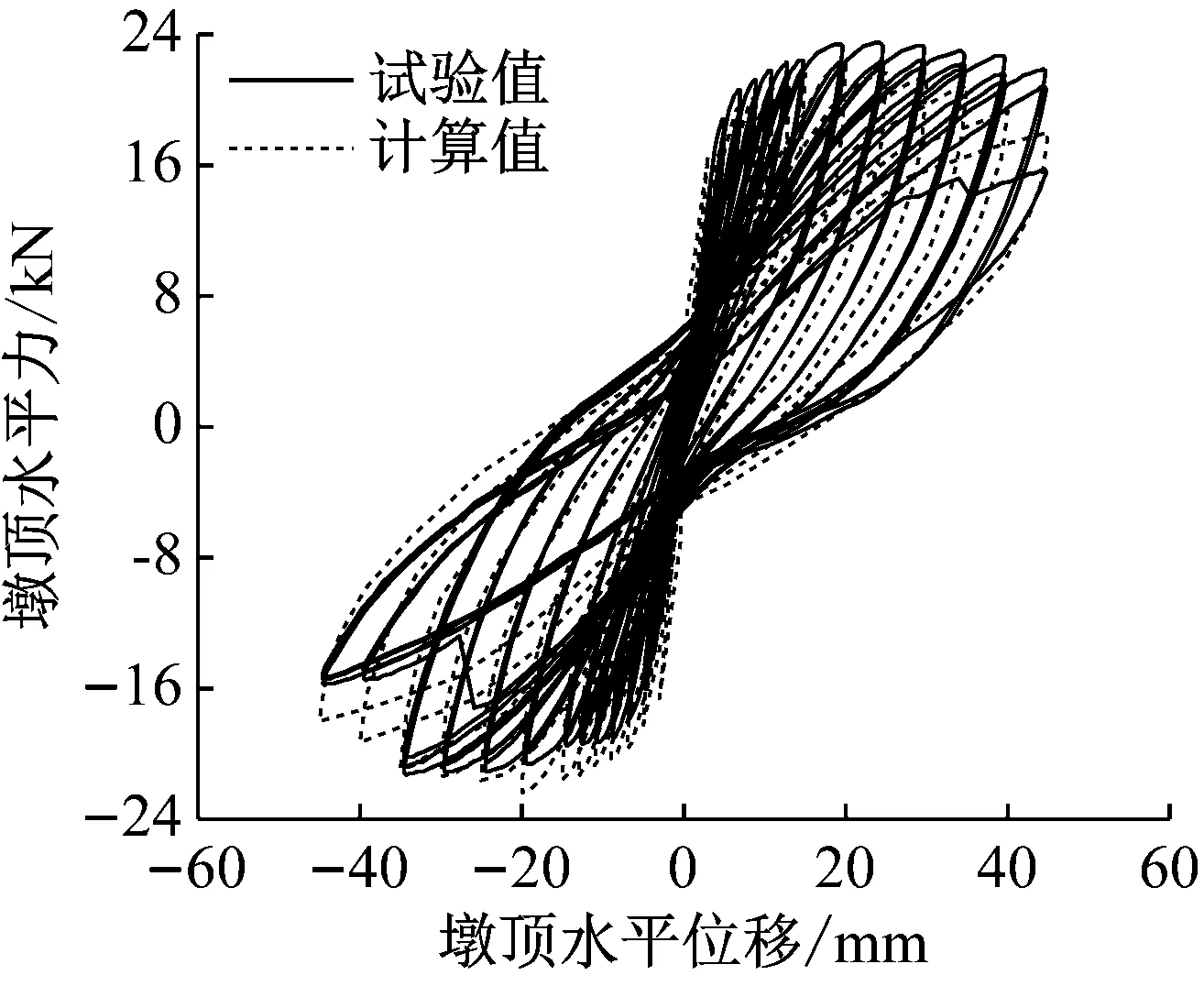
(a) S1橋墩

計算得到的滯回曲線與試驗結果對比發現，配筋率為0.2%的橋墩滯回曲線計算值與試驗結果吻合較好；隨著配筋率的增加，計算得到的滯回曲線相比于試驗結果的“捏縮”效應更為明顯。計算得到橋墩的骨架曲線與試驗結果吻合較好，通過極限承載力的對比發現(如表2所示)，配筋率較小時，計算值比試驗值偏高，而配筋率較大的橋墩，試驗值比計算值偏高，但最大誤差在8%以內。說明簡化的四彈簧模型可以預測低配筋的鐵路重力式橋墩在靜力作用下的水平承載力，能有效的模擬橋墩的受力特性，驗證了簡化四彈簧模型計算低配筋鐵路重力式橋墩抗震性能的準確性和合理性。

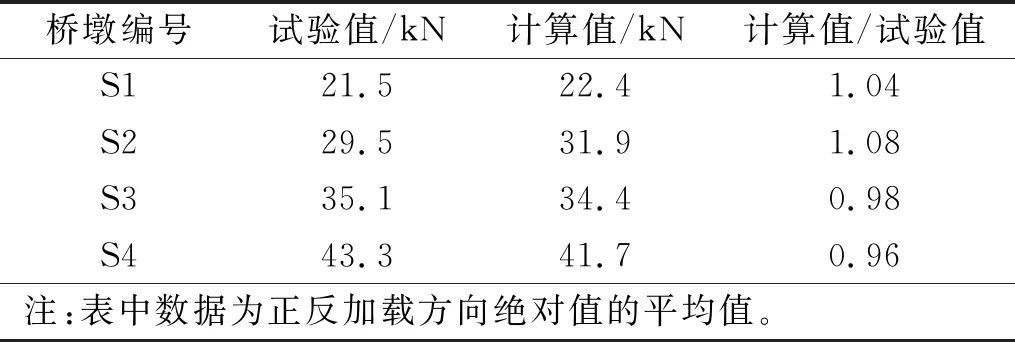
表2 極限承載力對比Tab.2 Comparisons of ultimate loads

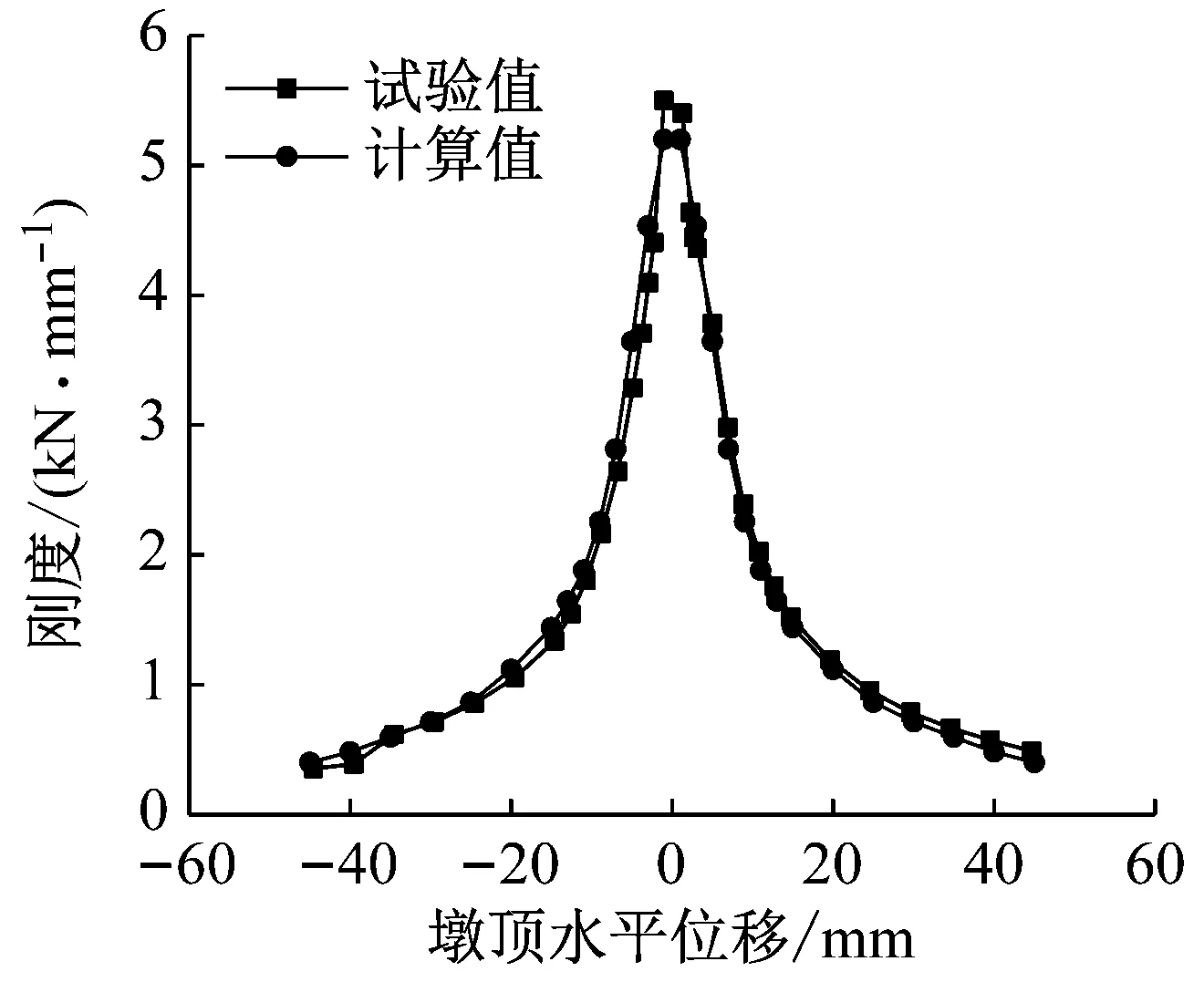
分析得到橋墩試驗值和計算值的剛度退化曲線，如圖6所示。

(a) S1橋墩

(a) S1橋墩

由圖6可以看出，計算得到橋墩的剛度退化曲線與試驗結果基本吻合。加載初期，橋墩剛度的試驗值比計算值偏高；當橋墩開裂后，且墩頂加載位移較小時，橋墩剛度的計算值比試驗值偏大；加載后期，計算值與試驗值基本吻合。橋墩剛度退化計算值與試驗值的變化趨勢基本一致，說明簡化模型可有效模擬橋墩的剛度退化特性。

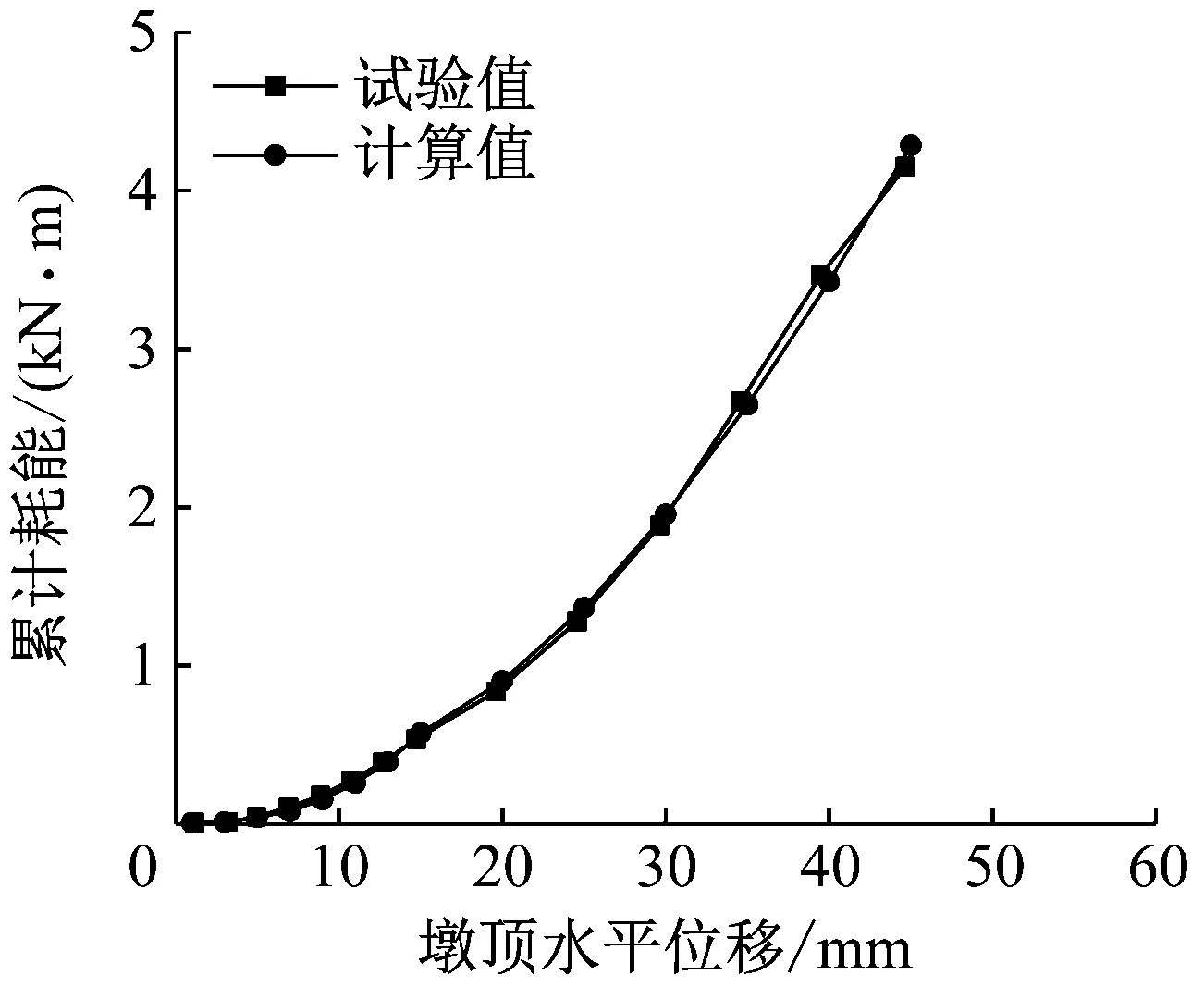
由圖7可以看出，配筋率為0.2%的橋墩，計算得到的累計耗能與試驗結果吻合較好；隨著配筋率的增大，計算結果與試驗結果誤差逐漸增大，其主要原因可能是試驗中正反加載方向無法完全對稱，骨架曲線(圖5)中可以明顯的看到，墩頂加載位移小于20 mm時，正向加載的承載力的計算值比試驗值偏大，最終導致計算結果的滯回環所包含的面積比試驗結果偏大。

(a) S1橋墩

采用四彈簧抗震分析模型對橋墩進行了動力響應分析，得到模型橋墩的墩頂相對位移和墩頂絕對加速度的響應，并與試驗值進行比較如圖8所示。在進行每個工況的試驗前對模型橋墩輸入白噪聲，測得結構的頻率，7度設計地震和8度罕遇地震前模型橋墩的頻率分別為8.9 Hz和8.3 Hz，四彈簧模型計算的頻率均為8.5 Hz。

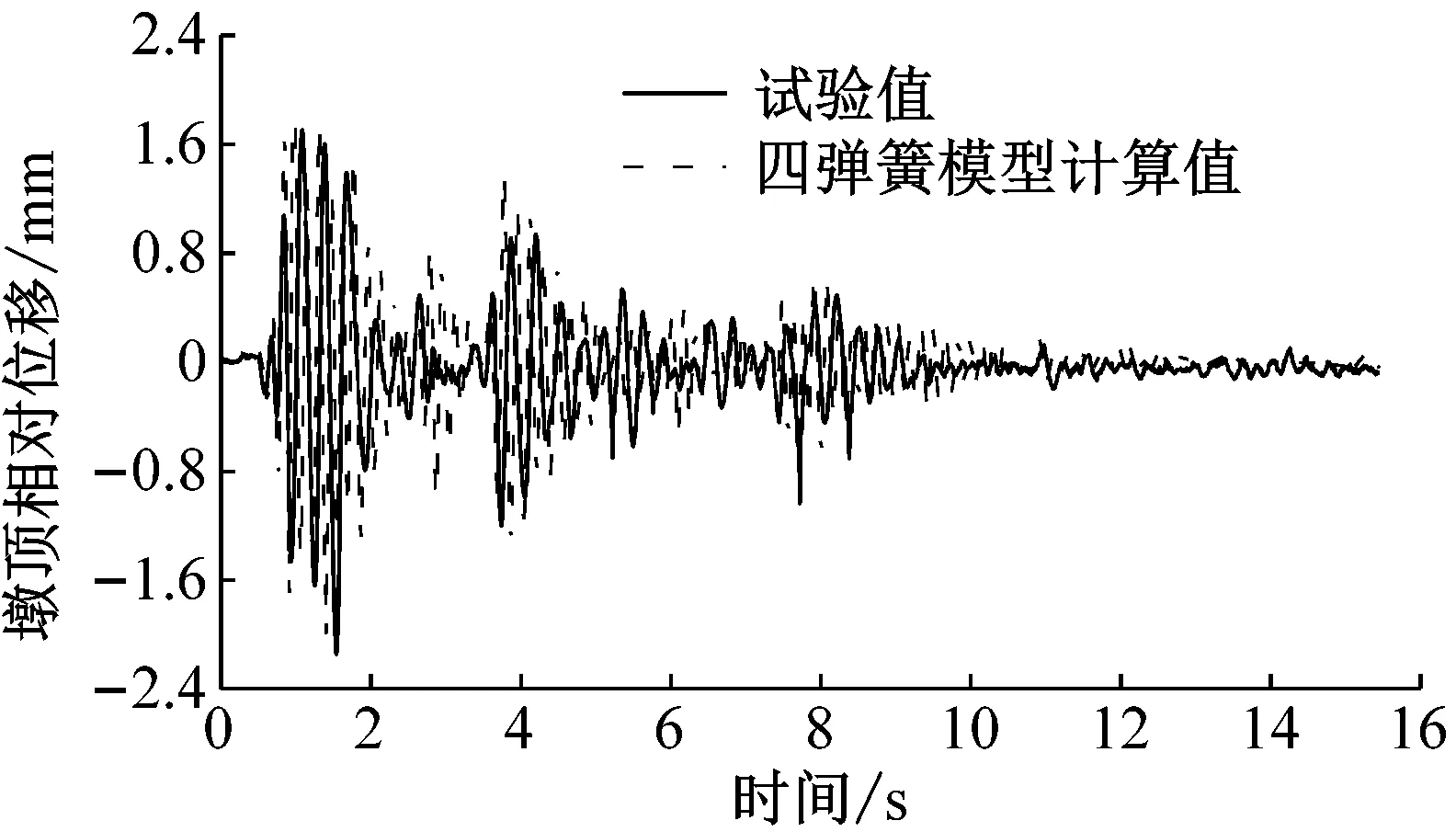
(a) 7度設計地震作用下墩頂相對位移

由圖8中可以看出，7度設計地震作用下墩頂相對位移及絕對加速度的四彈簧模型計算值與試驗值吻合較好；8度罕遇地震下墩頂相對位移四彈簧模型計算為9.13 mm，試驗值為10 mm，誤差僅為4.7%，墩頂絕對加速度四彈簧模型計算值為0.366g，試驗值為0.35g，誤差為4.6%。說明簡化的四彈簧模型可有效模擬橋墩的墩頂相對位移及墩頂絕對加速度，同時驗證了四彈簧模型計算橋墩動力響應的準確性和合理性。

3 結 論

通過鐵路重力式橋墩試驗及數值分析模型研究得到如下結論：

(1) 基于配筋率較低的鐵路重力式橋墩的破壞現象，在自由搖擺橋墩雙彈簧模型的基礎上，增加考慮鋼筋約束的非線性受拉彈簧，提出了適用于低配筋鐵路重力式橋墩的四彈簧模型抗震分析模型。

(2) 依據試驗模型結果，確定了只受拉彈簧剛度計算參數取值。鋼筋面積取受拉區縱向鋼筋面積之和，鋼筋計算高度可取等效塑性鉸長度。

(3) 靜力作用下和動力作用下，四彈簧模型計算值與試驗值均吻合加好，驗證了四彈簧抗震分析模型可用于鐵路重力式橋墩的抗震性能分析及動力響應分析。