串列多方柱氣動特性的試驗研究

楊 群，吳倩云，姜會民，陶 韜，劉小兵

(1.石家莊鐵道大學 省部共建交通工程結構力學行為與系統安全國家重點實驗室，石家莊 050043；2.河北省風工程和風能利用工程技術創新中心，石家莊 050043；3.石家莊鐵道大學 土木工程學院，石家莊 050043)

多方柱的結構布置形式在實際工程中廣泛應用，如高層建筑群、橋墩、橋塔、海上鉆井平臺的墩柱等。串列多方柱為多方柱的典型布置形式，因串列多方柱的繞流伴隨著流動的分離、再附著以及旋渦脫落等復雜的流動現象，從而使流動狀態與單方柱相比有很大差異，故引起了許多學者的關注。

Sakamoto等[1]通過試驗的方法研究了不同間距比下串列雙方柱的升阻力系數等，發現串列雙方柱在間距比(方柱中心間距與特征尺寸的比)4前后有不同的流動狀態。陳素琴等[2]通過數值計算的方法也再現了阻力系數在臨界間距時出現不連續跳躍的現象。杜曉慶等[3]通過風洞試驗的方法不僅發現串列雙方柱在臨界間距前后氣動特性會發生突變，而且發現氣動力的柱間相關性和柱內相關性與雙方柱的風壓非高斯區域均隨間距比變化較大。Kim等[4]則通過粒子圖像測速的方法研究了串列雙方柱在不同間距不同雷諾數時的速度、湍流強度和雷諾切應力等，發現流動的突然改變是由于上游方柱分離剪切層的再附著。也有一些學者[5-6]發現臨界間距隨雷諾數變化。Liu等[7]則通過試驗，研究了不同雷諾數下串列雙方柱在不同間距比時的流動特性，發現間距遞增和遞減時，所有雷諾數下均存在兩種不連續跳躍的現象。韓寧等[8]通過風洞試驗的方法，分析了串列雙方柱中施擾模型高度和位置變化時，對受擾方柱迎風面局部脈動風壓的影響。More等[9]則利用多種方法研究了上游方柱振蕩、下游方柱靜止的串列雙方柱在不同間距比時，方柱周圍流體的流動。

Sayers[10]利用風洞試驗的方法通過對串列三方柱升阻力系數和風壓分布的研究，發現小間距比時，中、下游方柱的阻力系數為負，之后變為正值但依然受上游方柱的影響。另外有一些學者將串列三方柱隨間距比的流動狀態進行了劃分。Islam等[11]通過數值計算的方法，發現串列三方柱在雷諾數為90～175，間距比在0.5～6時可以分為七種不同的流動狀態，并分析了升阻力系數等隨流動狀態的變化。鄭欽敏[12]也通過數值計算的方法研究了雷諾數為150時，串列三方柱隨間距比的流動特征，通過對速度、渦量等的分析，確定了四種不同的流動狀態和相應的方柱中心間距區間。Abbasi等[13]則利用數值模擬的方法研究了不同間距比時串列雙方柱、串列三方柱和串列四方柱在不同雷諾數時的流動狀態，發現間距比為2時，增加方柱數量每種流動狀態的雷諾數范圍減小，而間距比為5時，趨勢相反。

綜上所述，對于串列雙方柱的研究比較全面、詳細，運用試驗和數值模擬等多種方法不僅發現在臨界間距前后阻力系數會發生突變，而且發現雙方柱的速度、湍流強度和非高斯區域均存在較大的變化，并且說明了流動突然改變的原因，以及不同雷諾數時臨界間距的變化等。對于串列三方柱的研究較少，多為研究低雷諾數下串列三方柱在不同間距的流動狀態。但鮮有學者比較串列雙方柱和串列三方柱氣動特性的干擾效應，同時前人對于串列三方柱的研究雷諾數較小。本文通過剛性模型風洞試驗的方法，研究了雷諾數為3.2×104時，串列雙方柱和串列三方柱的氣動特性，以及方柱串列布置時，增加方柱數量對已有雙方柱氣動特性的影響。

1 風洞試驗概況

試驗在石家莊鐵道大學的大氣邊界層風洞實驗室的低速試驗段進行，低速試驗段寬4.38 m，高3 m，試驗段長24 m，最大風速約30 m/s，湍流度小于0.5%。

(a) 主視圖

為調節模型之間的間距，設計了如圖1所示的試驗裝置，模型通過自制剛架固定在低速試驗段，通過移動方柱的相對位置即可改變方柱的間距比。在實際工程中，大多數方柱結構頂部均存在三維繞流效應。本著由易到難的原則，本試驗僅考慮二維方柱的情況。為消除模型的端部效應，保證流場的二元性，在模型兩端布置了端板。

圖2為模型的參數定義及相對位置，模型間距比L/D(L為方柱的中心距，D為方柱的邊長)的取值分別為1.2、1.4、1.6、1.8、2.0、2.5、3.0、3.5、4.0、4.5、5.0、6.0、7.0、8.0。

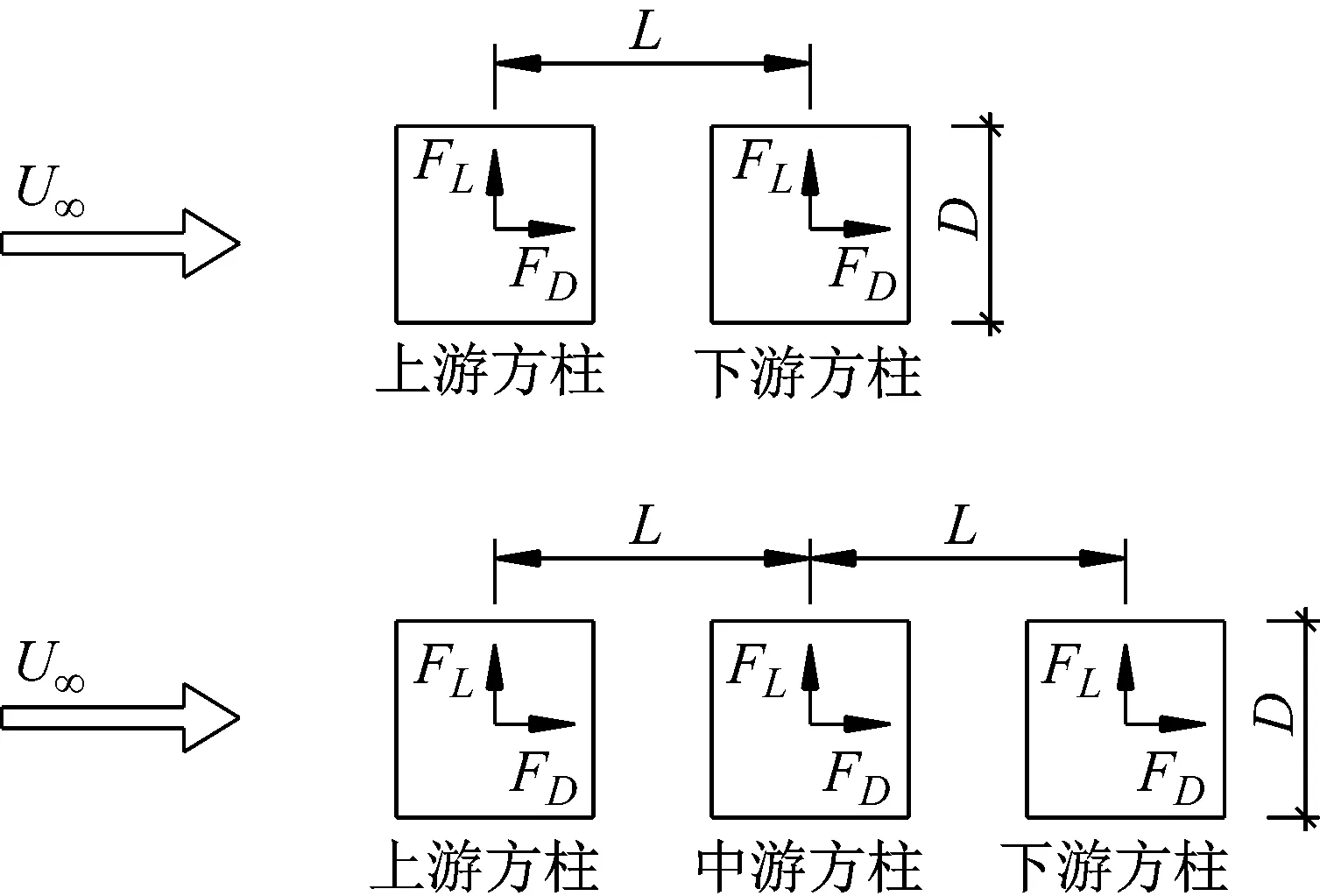
圖2 試驗模型的參數定義及相對位置Fig.2 Geometry parameters and relative location of test models

模型由ABS板制作而成，高度H=2 000 mm，橫斷面邊長D=80 mm。在模型的中央位置沿周向布置一圈測壓孔，共60個測點。考慮到流場參數在模型棱角附近變化較為劇烈，故對這些位置的測壓孔進行加密，同時為描述方便在方柱角點進行編號，測點布置如圖3所示。模型表面不同位置測壓孔的風壓通過電子壓力掃描閥測得，電子壓力掃描閥的采樣頻率為330 Hz，采樣時間為30 s。

圖3 試驗模型的測點布置(mm)Fig.3 Pressure tap arrangement of test mode(mm)

實際工程中的方柱結構均處在特定的紊流風場中。本著由淺入深，循序漸進的原則，本試驗僅在低湍流度的均勻流場中進行了研究。試驗阻塞度約為1.2%，小于5%，故不需要對試驗結果進行修正。

2 試驗結果與分析

2.1 氣動力特性

前人的研究表明串列雙方柱的氣動力會在特定的間距比下發生跳躍，此間距比稱為臨界間距比。Sakamoto等認為平均阻力系數突然變化的原因為臨界間距比前后存在兩種不同的流動狀態，小于臨界間距比時上游方柱分離的剪切層重新附著到下游方柱，并在兩柱之間形成半穩定渦區(quasi-steady vortex region)，大于臨界間距比時，雙方柱的尾流均會形成周期性的渦街。文獻[3-6]中串列雙方柱的臨界間距比在3～4.3。圖4和圖5分別為多方柱平均阻力系數和脈動升力系數隨間距比的變化曲線，由圖可看出：(1)串列雙方柱的平均阻力系數和脈動升力系數均在L/D=3～3.5時發8較大的跳躍現象，所以臨界間距比為3<(L/D)cr<3.5。臨界間距比與文獻[3]的結果吻合。(2)串列三方柱的上游方柱氣動力系數在間距比L/D=3.5～4時發生跳躍。中、下游方柱的氣動力系數在間距比L/D=2.5～3和L/D=3.5～4時均發生跳躍，所以串列三方柱存在兩個臨界間距比，分別為2.5<(L/D)cr1<3和3.5<(L/D)cr2<4。

2.1.1 平均阻力系數

不同間距比下方柱的氣動力可用無量綱參數阻力系數表示，定義為

(1)

式中：FD(i)為各測點壓力積分得到的方柱單位長度上的順風向阻力時程；ρ為空氣密度；U∞為模型遠前方來流的風速；D為模型特征尺寸。

平均阻力系數定義如下

(2)

式中,N為采樣點數。

圖4為串列雙方柱和串列三方柱平均阻力系數隨間距比的變化曲線，由圖4可以看出：

圖4 多方柱平均阻力系數隨間距比的變化Fig.4 Variation of the average drag coefficient of square cylinders at different spacing ratios

對于串列雙方柱：小于臨界間距比(L/D)cr時(L/D≤3)，上游方柱的平均阻力系數隨間距比的增大在1.75左右小幅波動，小于單方柱的值，下游方柱平均阻力系數隨間距比的增大逐漸減小且均為負值，此時雙方柱平均阻力系數的干擾效應均表現出減小效應但下游方柱的減小效應更為顯著。大于臨界間距比(L/D)cr時(L/D≥3.5)，上游方柱的平均阻力系數隨間距比的增大逐漸增大且逐漸接近單方柱的值，下游方柱的平均阻力系數隨間距比的增大逐漸減小且逐漸接近0.7。此時上游方柱平均阻力系數的干擾效應不再明顯，下游方柱平均阻力系數的減小效應減弱。

對于串列三方柱：(1)小于臨界間距比(L/D)cr1時(L/D≤2.5)，上游方柱的平均阻力系數隨間距比先略微增大后緩慢減小，且平均阻力系數的值均處于1.5附近。中游方柱的平均阻力系數隨間距比逐漸減小，下游方柱的平均阻力系數隨間距比逐漸增大，且中、下游方柱的平均阻力系數均為負值。此時，三個方柱平均阻力系數的干擾效應均表現出明顯的減小效應，且中、下游方柱的減小效應更為明顯。這與文獻[12]的變化規律相同但數值不同，這可能是由于雷諾數不同導致的。(2)間距比從2.5增大到3時，中游方柱平均阻力系數突然下降，下游方柱則相反。(3)在兩個臨界間距比之間時(3≤L/D≤3.5)，上游方柱仍受到中、下游方柱的干擾，平均阻力系數的干擾效應表現出明顯的減小效應。中游方柱的平均阻力系數仍為負值，下游方柱的平均阻力系數為正值，中、下游方柱平均阻力系數的干擾效應較上游方柱表現出更為明顯的減小效應，且中游方柱的減小效應最為顯著。(4)間距比從3.5增大到4時，中游方柱的平均阻力系數突然增加，而下游方柱的平均阻力系數突然減小。同時可以發現，在臨界間距比(L/D)cr1和(L/D)cr2前后，中、下游方柱平均阻力系數的變化趨勢相反。(5)大于臨界間距比(L/D)cr2時(L/D≥4)，三方柱的上、中游方柱平均阻力系數隨間距比的變化規律分別與雙方柱的上、下游方柱類似，三方柱的下游方柱平均阻力系數隨間距比的增大基本不變保持在0.35左右，且減小效應比中游方柱更顯著。

對比串列雙方柱和串列三方柱可以發現：雙方柱的上、下游方柱平均阻力系數隨間距比的變化分別與三方柱的上、中游方柱相似。小于臨界間距比(L/D)cr1時，三方柱的上游方柱較雙方柱的上游方柱平均阻力系數的減小效應更加顯著，但三方柱的中游方柱較雙方柱的下游方柱平均阻力系數的減小效應卻有所減弱。

2.1.2 脈動升力系數

脈動升力系數定義如下

(3)

(4)

式中,FL(i)為各測點壓力積分得到的方柱單位長度上的橫風向升力時程。

圖5為串列雙方柱和串列三方柱脈動升力系數隨間距比的變化曲線，由圖5可以看出：

圖5 多方柱脈動升力系數隨間距比的變化Fig.5 Variation of the fluctuating lift coefficient of square cylinders at different spacing ratios

對于串列雙方柱：小于臨界間距比(L/D)cr時(L/D≤3)，上游方柱的脈動升力系數隨間距比的增大逐漸減小，下游方柱的脈動升力系數隨間距比先輕微增大后緩慢減小。上、下游方柱脈動升力系數的干擾效應均表現出明顯的減小效應，且上游方柱的減小效應更顯著。大于臨界間距比(L/D)cr時(L/D≥3.5)，上游方柱的脈動升力系數隨間距比的增大逐漸減小，最后接近單方柱的值，下游方柱的脈動升力系數也隨間距比的增大逐漸減小。上游方柱脈動升力系數在間距比3.5附近表現出輕微的增大效應，其余間距比下干擾效應不明顯，下游方柱的脈動升力系數則是在間距比3.5附近干擾效應不明顯，其余間距比下表現出減小效應。本文的結果與文獻[1]的結果基本吻合。

對于串列三方柱：(1)小于臨界間距比(L/D)cr1時(L/D≤2.5)，三方的上游方柱脈動升力系數隨間距比的變化趨勢與雙方柱的上游方柱類似，三方柱的中、下游方柱脈動升力系數隨間距比的變化趨勢與雙方柱的下游方柱類似。上、中、下游方柱脈動升力系數的干擾效應均表現出明顯的減小效應，且上游方柱的減小效應最顯著，中游方柱次之，下游方柱再次之。下游方柱的脈動升力系數均大于其它方柱的值，鄭欽敏認為，這是由于此時只有下游方柱發生旋渦脫落。(2)在兩個臨界間距比之間時(3≤L/D≤3.5)，中、下游方柱脈動升力的減小效應有所減弱，上游方柱的干擾效應基本不變。這是由于上游方柱前緣分離的剪切層交替的再附到中游方柱的側面，其卷起(roll-up)發生在中游方柱的后面。(3)大于臨界間距比(L/D)cr2時(L/D≥4)，三方柱的上、中游方柱脈動升力系數隨間距比的變化規律分別與雙方柱的上、下游方柱類似。三方柱的下游方柱脈動升力系數隨間距比的增大逐漸減小。三方柱的下游方柱脈動升力系數的減小效應最為顯著，其次是中游方柱，最后為上游方柱。這與在臨界間距(L/D)cr1之前時正好相反。

對比串列雙方柱和串列三方柱可以發現，在臨界間距比(L/D)cr1之前時，三方柱的上、中游方柱脈動升力系數的減小效應分別較雙方柱的上、下游方柱更明顯。

2.2 風壓分布特性

2.2.1 平均風壓系數

不同間距比下方柱的風壓分布可用無量綱參數風壓系數表示，定義為

(5)

式中：Pi是模型表面某測點處測得的瞬時壓力信號的時間序列；Ps是參考點處的靜壓值。

平均風壓系數Cp,mean定義為

(6)

圖6為方柱迎風面(a-b面)的平均風壓系數分布云圖。由圖6可以看出：

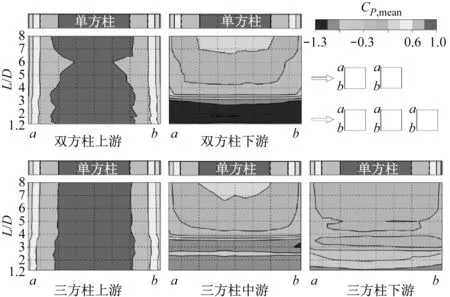
圖6 迎風面(a-b面)平均風壓系數分布云圖Fig.6 Contours of average pressure coefficient on surface(a-b)

對于串列雙方柱：上游方柱的平均風壓系數隨間距比基本不變，在迎風面的分布均呈現出中間大向兩端逐漸減小的變化趨勢，且與單方柱的值大致相同。上游方柱迎風面的平均風壓系數基本不受下游方柱的干擾。小于臨界間距比(L/D)cr時(L/D≤3)，下游方柱的平均風壓系數在迎風面上的值大致相同，集中在-1.3～-1.0，為風吸力，與單方柱有很大不同。這也可以說明此時雙方柱之間存在半穩定渦區。大于臨界間距比(L/D)cr時(L/D≥3.5)，下游方柱平均風壓系數的絕對值隨間距比的增大呈現出逐漸減小的變化趨勢，且均為中間部分的絕對值略小于兩端的絕對值，主要集中在-0.3～0，除7≤L/D≤8的中間部分為風壓力外，其余部分均為風吸力。下游方柱迎風面的風壓在臨界間距比時發生跳躍，風吸力減小。

對于串列三方柱：(1)三方柱上游方柱與雙方柱上游方柱的平均風壓系數隨間距比的變化規律基本一致，在迎風面的分布規律也基本一致。(2)三方柱中游方柱平均風壓系數的變化規律與雙方柱的下游方柱類似，不同的是，小于臨界間距比(L/D)cr時(L/D≤3)，三方柱的中游方柱平均風壓系數的值均集中在-1.0～-0.8，負壓略小于對應間距比時雙方柱的下游方柱。值得注意的是，在間距比L/D=2.5時，三方柱的中游方柱出現一個相對較小的負壓，在間距比L/D=3.5時，三方柱的中游方柱迎風面的負壓明顯大于雙方柱的下游方柱。(3)三方柱下游方柱平均風壓系數的絕對值隨間距比呈現出逐漸減小的變化趨勢，平均風壓系數絕對值的分布規律也均為中間部分略小于兩端，主要為負壓。同時可以發現，小于臨界間距比(L/D)cr1時(L/D≤2.5)，下游方柱平均風壓系數的值在-0.9～-0.5；在臨界間距比(L/D)cr1前后小幅跳躍；大于臨界間距比(L/D)cr1時(L/D≥3)，平均風壓系數的值集中在-0.25～0。對比三方柱的中、下游方柱可以發現：下游迎風面的負壓均小于對應間距比時中游方柱的負壓。

圖7為串列雙方柱和串列三方柱背風面(c-d面)的平均風壓系數分布云圖。由圖7可以看出：

圖7 背風面(c-d面)平均風壓系數分布云圖Fig.7 Contours of average pressure coefficient on surface(c-d)

對于串列雙方柱：上游方柱背風面的間距比小于臨界間距比(L/D)cr時(L/D≤3)，平均風壓分布均勻，平均風壓系數主要集中在-1.0附近，其絕對值低于單方柱的值；大于臨界間距比(L/D)cr時(L/D≥3.5)，平均風壓系數接近單方柱的值。而此時上游方柱迎風面在臨界間距比前后平均風壓系數基本不變，故上游方柱的平均阻力系數突然增大接近單方柱的值。下游方柱的間距比小于臨界間距比(L/D)cr時(L/D≤3)，背風面的負壓隨間距比逐漸減小，平均風壓系數在-0.75～-0.3。此時迎風面的負壓大于背風面的負壓，故下游方柱受反向推力；間距比從3增大到3.5時，背風面的負壓突然增大；大于臨界間距比(L/D)cr時(L/D≥3.5)，背風面的負壓仍隨間距比逐漸減小，平均風壓系數在-1.2～-0.6，此時迎風面的負壓小于背風面的負壓，所以平均阻力系數變為正值。

對于串列三方柱：(1)在背風面，三方柱的上、中游方柱平均風壓的分布分別與雙方柱的上、下游方柱類似。不同的是，三方柱的上、中游方柱在背風面的平均風壓系數發生跳躍的間距比為3.5

圖8為方柱側面(b-c面)的平均風壓系數分布云圖。由于平均風壓系數在兩個側面對稱，所以只給出了一個側面的分布云圖。由圖8可以看出：

圖8 側面(b-c面)平均風壓系數分布云圖Fig.8 Contours of average pressure coefficient on surface(b-c)

對于串列雙方柱：上游方柱的間距比小于臨界間距比(L/D)cr(L/D≤3)時，側面的平均風壓分布均勻且平均風壓系數主要集中在-1.0左右；大于臨界間距比(L/D)cr(L/D≥3.5)時，平均風壓系數的值接近單方柱的值，主要集中在-1.5左右。上游方柱側面的負壓突然增大到接近單方柱的值，這也可以證明剪切層再附流態轉變為雙渦脫流態。對比上游方柱的側面和背風面可以發現，其風壓分布類似。雙方柱的下游方柱平均風壓系數的絕對值隨間距比的變化為先逐漸減小后突然增大最后趨于平穩，但平均風壓系數的絕對值始終小于單方柱的值，且側面的負壓由b角點到c角點逐漸減弱。下游方柱側面的平均風壓系數在臨界間距比前后小幅跳躍。

對于串列三方柱：(1)三方柱上游方柱的側面平均風壓分布與雙方柱的上游方柱類似，但負壓略小于對應間距比時雙方柱的上游方柱，且在L/D=3.5時，負壓差距明顯。平均風壓系數發生跳躍的間距比也不同，三方柱時為3.5

2.2.2 脈動風壓系數

脈動風壓系數Cp,rms定義為

(7)

圖9為方柱迎風面(a-b面)的脈動風壓系數分布云圖。由圖9可以看出：

圖9 a-b面脈動風壓系數分布云圖Fig.9 Contours of fluctuating pressure coefficient on surface(a-b)

對于串列雙方柱：上游方柱脈動風壓系數隨間距比的變化規律大致可以分為兩部分：小于臨界間距比(L/D)cr(L/D≤3)時，脈動風壓系數在迎風面上分布均勻，主要集中在0～0.1，干擾效應表現出明顯的減小效應；大于臨界間距比(L/D)cr(L/D≥3.5)時，脈動風壓系數在迎風面的分布規律為中間小兩邊大，與單方柱的值接近。下游方柱的2脈動風壓系數在小于臨界間距比(L/D)cr(L/D≤3)時接近單方柱的值；大于臨界間距比(L/D)cr(L/D≥3.5)時，脈動風壓系數在迎風面的變化規律同樣為中間小兩端大，但此間距比下，脈動風壓系數的值大于單方柱的值，干擾效應表現出明顯的增大效應。

對于串列三方柱：(1)三方柱的上游方柱脈動風壓系數的變化規律和雙方柱的上游方柱類似，但三方柱的脈動風壓發生跳躍的間距比為3.5

圖10為方柱背風面(c-d面)的脈動風壓系數分布云圖。由圖10可以看出：

圖10 c-d面脈動風壓系數分布云圖Fig.10 Contours of fluctuating pressure coefficient on surface(c-d)

對于串列雙方柱：上游方柱脈動風壓系數在小于臨界間距比(L/D)cr(L/D≤3)時基本不變，集中在0.1附近，干擾效應表現出明顯的減小效應；大于臨界間距比(L/D)cr(L/D≥3.5)時，脈動風壓系數接近單方柱的值，干擾效應不明顯。下游方柱的脈動風壓系數在背風面表現出中間小兩端大的分布規律。在小于臨界間距比(L/D)cr(L/D≤3)時，下游方柱的脈動風壓小于單方柱的值，干擾效應表現出明顯的減小效應；大于臨界間距比(L/D)cr(L/D≥3.5)時，下游方柱的脈動風壓隨間距比的增大逐漸減小，間距比為5時接近單方柱的值。

對于串列三方柱：(1)三方柱的上游方柱脈動風壓系數的變化規律與雙方柱的上游方柱類似，但脈動風壓發生跳躍的間距比不同。(2)三方柱的中游方柱脈動風壓系數的變化規律與雙方柱的下游方柱類似，不同的是：三方柱中游方柱的脈動風壓存在兩個跳躍的間距比，且L/D=3.5時三方柱中游方柱的脈動風壓系數明顯小于雙方柱下游方柱的值。在兩個臨界間距比之間(3≤L/D≤3.5)時，中游方柱背風面的脈動風壓介于臨界間距比(L/D)cr1之前(L/D≤2.5)和臨界間距比(L/D)cr2之后(L/D≥4)的值。(3)下游方柱脈動風壓系數在背風面的分布規律為兩端略大于中間，干擾效應表現出明顯的減小效應。小于臨界間距比(L/D)cr1(L/D≤2.5)和大于臨界間距比(L/D)cr2(L/D≥4)時，脈動風壓系數主要集中在0.1左右，在兩個臨界間距比之間(3≤L/D≤3.5)時，脈動風壓系數略大于其它間距比的值。

圖11為方柱側面(b-c面)的脈動風壓系數分布云圖。同樣由于兩側面的脈動風壓具有對稱性，所以只給出了一側的云圖。由圖11可以看出：

圖11 b-c面脈動風壓系數分布云圖Fig.11 Contours of fluctuating pressure coefficient on surface(b-c)

對于串列雙方柱：上游方柱脈動風壓系數在臨界間距比前后發生跳躍。小于臨界間距比(L/D)cr(L/D≤3)時，脈動風壓系數在側面分布均勻，數值很小。大于臨界間距比(L/D)cr(L/D≥3.5)時，脈動風壓系數的值接近單方柱的值。因為此時，上、下游方柱都開始出現周期性的旋渦脫落，尾流波動幅度較大。下游方柱的脈動風壓系數在小于臨界間距比(L/D)cr(L/D≤3)時的干擾效應表現出明顯的減小效應；大于臨界間距比(L/D)cr(L/D≥3.5)時，脈動風壓系數由角點b到c逐漸減小，且在角點b附近大于單方柱的值，在角點c附近小于單方柱的值。Sakamoto等認為，這可能是由于上游方柱產生的非常大的湍流強度導致剪切層的間歇性重新附著而造成的。

對于串列三方柱：(1)除臨界間距比不同外，三方柱的上游方柱和雙方柱的上游方柱脈動風壓系數變化規律相似。(2)中游方柱被臨界間距比劃分為三個部分，小于臨界間距比(L/D)cr1時(L/D≤2.5)，脈動風壓系數由角點b到c小幅增加，且主要集中在0～0.2內；在兩個臨界間距比之間時(3≤L/D≤3.5)，脈動升力系數較臨界間距比(L/D)cr1之前時(L/D≤2.5)略微增加，但干擾效應仍表現出明顯的減小效應；大于臨界間距比(L/D)cr2時(L/D≥4)，三方柱中游方柱的脈動風壓與雙方柱的下游方柱類似，但三方柱脈動風壓系數的值略小。(3)下游方柱側面的波動由角點b到c逐漸減弱，且脈動風壓系數在角點c處基本不隨間距比的變化，集中在0.1附近。下游方柱的脈動風壓系數在兩個臨界間距比之間(3≤L/D≤3.5)時，略大于其他間距比的值。對比三方柱的中、下游方柱可以發現：小于臨界間距比(L/D)cr2(L/D≤3.5)時，下游方柱各面的脈動風壓系數均略大于中游方柱的值，在臨界間距比(L/D)cr2之后(L/D≥4)時，下游方柱各面的脈動風壓系數的值均略小于中游方柱。

2.3 旋渦脫落特性

不同間距比下方柱的旋渦脫落特性可用無量綱參數斯托羅哈數表示，其定義如下

(8)

式中,f為旋渦脫落頻率。

圖12為對串列雙方柱和串列三方柱的升力系數時程進行傅里葉變換得到的不同間距比下雙方柱和三方柱的幅值譜圖。由圖12可以清楚的看出不同間距比下方柱的斯托羅哈數和幅值的變化情況。

雙方柱的上游方柱(圖12(a))和下游方柱(圖12(b))的幅值在臨界間距比3<(L/D)cr<3.5前后發生了明顯的跳躍現象，幅值突然增大。三方柱上游方柱(圖12(c))的幅值在臨界間距比3.5<(L/D)cr2<4前后發生跳躍，幅值增大；三方柱中游方柱(圖12(d))的幅值在臨界間距比2.5<(L/D)cr1<3和3.5<(L/D)cr2<4時發生跳躍，幅值均增大；三方柱下游方柱(圖12(e))的幅值在臨界間距比2.5<(L/D)cr1<3前后突然增大，在3.5<(L/D)cr2<4前后突然減小。雙方柱和三方柱的幅值在臨界間距比前后的變化情況均與脈動升力系數的變化情況吻合。

(a) 雙方柱的上游方柱

圖13為串列多方柱的斯托羅哈數隨間距比的變化規律。由圖13可以看出：

圖13 串列多方柱斯托羅哈數隨間距比的變化曲線Fig.13 Variation of Strouhal number of cylinders at different spacing ratios

串列雙方柱的上游方柱和下游方柱在不同間距比下斯托羅哈數的值大致相等，這與文獻[3]和[14]的結果一致。斯托羅哈數隨間距比的變化規律為先增大后減小最后逐漸增大，除間距比為1.6時大于單方柱的值，其余間距下始終小于單方柱的值。雙方柱的斯托羅哈數在間距比為1.6時取得極大值，極大值為0.132，在間距比為4時取得極小值，極小值為0.102。

串列三方柱的上、中、下游方柱的斯托羅哈數在不同間距比時也大致相等，但上游方柱在間距比為2.5時，下游方柱在間距比為8時，不存在斯托羅哈數。斯托羅哈數隨間距比的變化規律為先增大后減小再增大。三方柱的斯托羅哈數在間距比為1.8時取得極大值，極大值為0.106，在間距比為3.5時取得極小值，極小值為0.097。

對比串列雙方柱和串列三方柱可以發現，當小于臨界間距比(L/D)cr2時，雙方柱和三方柱斯托羅哈數的差別較大，且隨著間距比的增大差距逐漸縮小，當大于臨界間距比(L/D)cr2時，雙方柱和三方柱的斯托羅哈數差距不再顯著。

2.4 氣動特性機理的初步分析

2.4.1 數值計算方法

為了對串列多方柱氣動特性的產生機理進行分析，基于雷諾平均法和SSTk-ω湍流模型，對串列雙方柱和串列三方柱進行了數值模擬。數值計算選取的間距比為L/D=2和L/D=5，分別小于和大于臨界間距。圖14為串列雙方柱和串列三方柱的計算區域和計算模型，方柱邊長D=80 mm，兩方柱中心間距為L，上游方柱中心距入口20D，下游方柱中心距出口35D，方柱中心距兩側均為20D。入口采用速度入口邊界條件，出口采用自由出口邊界，兩側壁面采用對稱邊界，方柱表面采用無滑移壁面邊界條件。

(a) 串列雙方柱

數值計算采用基于壓力的非穩態求解器，SIMPLEC算法求解壓力速度耦合方程。數值模擬的雷諾數與試驗相同。方柱近壁面網格y+≈1，殘差值控制精度為10-5。計算網格采用結構化網格，在柱體周圍加密，網格劃分如圖15所示。

(a) L/D=2串列雙方柱

2.4.2 數值模擬結果

表1為數值模擬與風洞試驗得到的平均阻力系數對比。由表可知，風洞試驗和數值模擬得到的平均阻力系數總體上相差不大。

表1 數值模擬與風洞試驗平均阻力系數結果對比Tab.1 Comparison of computation and experiment for mean drag coefficient

圖16為多方柱的時均風速流線圖，圖17為多方柱的瞬時渦量圖。由圖16和17可以看出，單方柱尾部存在明顯的卡門渦。對于串列雙方柱，當間距比為2時，由于下游方柱的存在，上游方柱后方的卡門渦被抑制，所以上下游方柱的脈動升力系數遠小于單方柱的值。由于上游方柱的遮擋，下游方柱的來流風速明顯減小，因此其平均阻力系數遠小于單方柱的值。當間距比為5時，上游方柱尾部形成卡門渦，與單方柱類似，所以上游方柱的脈動升力系數和平均阻力系數均與單方柱的值接近。下游方柱受上游方柱影響，來流速度仍有所減小，所以下游方柱平均阻力系數仍小于單方柱的值。

(a) 單方柱

(a) 單方柱

對串列三方柱，間距比為2時，上游方柱和中游方柱尾部的卡門渦均被抑制，同時下游方柱尾部的旋渦強度也明顯減弱，所以上、中、下游方柱的脈動升力系數均明顯小于單方柱的值。當間距比為5時，上游方柱的卡門渦與單方柱相似，脈動升力系數接近單方柱的值；中游方柱受上游方柱的影響，來流風速減小，所以脈動升力系數和平均阻力系數均小于單方柱的值；下游方柱受上游和中游方柱的共同遮擋，來流速度進一步減小，因此脈動升力系數和平均阻力系數小于中游方柱的值。

3 結 論

通過對比串列雙方柱和串列三方柱在不同間距比下的風壓分布、氣動力系數和斯托羅哈數等，得到了如下結論：

(1) 串列雙方柱存在單一臨界間距比，為3<(L/D)cr<3.5。串列三方柱存在兩個臨界間距比，分別為2.5<(L/D)cr1<3和3.5<(L/D)cr2<4。

(2) 在串列雙方柱的下游增加一個方柱后，當小于臨界間距比(L/D)cr1時，順風向第一個方柱平均阻力和脈動升力的減小效應更加顯著，第二個方柱平均阻力的減小效應有所減弱，脈動升力的減小效應更加明顯。當大于臨界間距比(L/D)cr2時，上游兩方柱的氣動力基本不隨下游方柱的增加而變化。當在兩個臨界間距比之間時，上游兩方柱的氣動力減小效應均更顯著。新增方柱在(L/D)cr1前后氣動力均突然增大，在(L/D)cr2前后則相反。

(3) 串列雙方柱下游增加一個方柱后，順風向第一個方柱的平均風壓系數和脈動風壓系數隨間距比的風壓分布變化不大，但絕對值略有不同，順風向第二個方柱在(L/D)cr1和(L/D)cr2時發生跳躍。原有方柱在間距比為3.5時的風壓與雙方柱時差別較大。

(4) 串列雙方柱和三方柱的斯托羅哈數隨間距的變化規律相似，但具體數值有所差別。當小于臨界間距比(L/D)cr2時，串列三方柱的斯托羅哈數明顯小于串列雙方柱的斯托羅哈數；當大于臨界間距比(L/D)cr2時，二者差別不大。