新疆果園深施散體廄肥離散元參數標定研究

韓樹杰 戚江濤 坎 雜 李亞萍 蒙賀偉

(1.石河子大學機械電氣工程學院， 石河子 832003； 2.農業農村部西北農業裝備重點實驗室， 石河子 832003)

0 引言

新疆地區廄肥資源較為豐富，施用廄肥可促進果園土壤微生物的生命活動，對提高土壤肥力、改善土壤結構、補充土壤養分和創造良好的土壤生態環境具有重要作用[1-3]。

近年來，隨著計算機技術的發展，離散元法(Discrete element method, DEM)在農業裝備研究上應用越來越廣泛[4-8]。利用離散元法全面、系統研究散體物料和機械裝置之間的相互作用機理和物料的運動狀態，不僅可以優化機械裝置的結構參數和工作參數，而且可以提高研發效率、改善機械作業性能、節約成本。物料離散元參數標定是研究物料與機械裝置之間相互作用的基礎。GRIMA等[9]利用崩塌試驗中的顆粒堆休止角對干顆粒在離散元仿真中所需滾動摩擦因數進行了標定；BOAC等[10]運用離散方法模擬了精選油籽顆粒的材料和相互作用特性；溫翔宇等[11]對顆粒肥料進行離散元仿真，標定了顆粒肥的摩擦因數；袁全春等[12]對有機肥散體顆粒離散元模型進行參數標定，仿真休止角與實際休止角的相對誤差僅為0.42%；羅帥等[13]基于JKR粘結模型標定了蚯蚓糞基質的離散元參數，休止角仿真結果與實際試驗結果較為接近；文獻[14-17]分別對粘性土壤、沙土顆粒土壤的模型參數進行了標定，結果表明，虛擬仿真結果與實測值之間差異較小。

本文在以上研究基礎上，以新疆果園深施散體廄肥為研究對象，采用仿真試驗與物理試驗相結合的方法，對散體廄肥的離散元參數進行標定，從而獲得散體廄肥的離散元模型，以期為全面、系統研究肥料和施肥裝置之間的相互作用機理以及物料的運動狀態提供參考。

1 材料與方法

1.1 試驗材料

試驗所用廄肥為新疆生產建設兵團第八師一二一團葡萄園用廄肥，由純牛糞發酵，發酵時間為3～4個月。前期試驗結果表明，為保證施肥機作業性能，提高施肥機施肥均勻性和穩定性，施肥前需對廄肥進行粉碎處理。用環刀法測定所選廄肥的密度；選取500 g廄肥作為試驗樣本，使用土壤標準粒徑篩(篩孔直徑0.25～5 mm)確定其粒徑分布情況；用MH45型含水率測定儀(質量測量精度0.001 g,含水率測量精度0.01%)測定廄肥的含水率；堆積角試驗中所用鋼板材質為45號鋼，參照文獻[18-20]確定所選材料的泊松比、剪切模量，材料的基本性質如表1所示，本征參數如表2所示。

表1 廄肥基本性質Tab.1 Basic properties of manure

表2 廄肥、鋼本征參數Tab.2 Intrinsic parameters of manure and steel plate

1.2 試驗方法

肥料顆粒的自然堆積角能反映其流動、摩擦等特性[21],本文采用物理試驗與仿真試驗相結合的方法[22-23]對廄肥離散元模型參數進行標定，采用注入法對廄肥進行堆積角試驗，并在EDEM離散元仿真軟件中進行仿真，應用Design-Expert 8.0.6軟件進行Plackett-Burman多因素顯著性篩選試驗與分析，得出對堆積角有顯著性影響的參數；在此基礎上，通過Box-Behnken響應面分析法建立并優化廄肥堆積角與顯著性參數的回歸模型，以實際堆積角為目標值對回歸方程求解尋優，得到顯著性參數最優值。最后在最優參數下進行仿真試驗，對比廄肥仿真堆積角和實際堆積角，驗證標定的廄肥離散元模型參數的準確性。

1.3 物理模型

結合文獻[24-26]對堆積角的相關研究，試驗參照GB 11986—89/ISO 4324—1977《表面活性劑粉體和顆粒休止角的測量》，采用注入法測量散體廄肥的堆積角，測量裝置如圖1所示，漏斗下口內徑為10 mm，錐度為60°，托盤直徑為100 mm，高度為25 mm，漏斗的下端口與托盤上表面距離為75 mm。試驗時，漏斗中的廄肥顆粒經漏斗口落于托盤上，最終在托盤上形成穩定的顆粒堆，在側面對堆積角拍照，采用Matlab對圖像進行處理以獲得廄肥顆粒的堆積角。重復5次試驗取其平均值，試驗得到廄肥的堆積角為35.47°。

2 廄肥堆積角仿真試驗

2.1 顆粒間接觸模型

在EDEM接觸模型理論中，Hertz-Mindlin with JKR Cohesion模型是一個凝聚力接觸模型，該接觸模型在Hertz接觸理論的基礎上結合JKR理論，考慮濕顆粒間粘結力對顆粒運動的影響，適用于模擬顆粒間因水分發生明顯粘結和團聚的物料[14]。在該模型中，法向彈性接觸力的實現基于Johnson-Kendall-Roberts理論，切向彈性力、法向耗散力和切向耗散力均與Hertz-Mindlin(no slip)接觸模型中的計算方法一致，在Johnson-Kendall-Robert理論中，JKR法向彈性力的實現基于重疊量δ、相互作用參數和表面能。計算式為

(1)

(2)

其中

(3)

(4)

式中FJKR——JKR法向彈性力，N

α——相互接觸2個顆粒的接觸圓半徑，m

γ——表面能，N/m

E*——等效彈性模量，Pa

R*——等效半徑，m

Ei、Ej——相互接觸2個顆粒的彈性模量，Pa

vi、vj——相互接觸2個顆粒的泊松比

Ri、Rj——相互接觸2個顆粒的半徑，m

當γ=0時，力變為Hertz-Mindlin法向力

(5)

即使顆粒并不是直接接觸，該模型也提供吸引凝聚力，顆粒間具有非凝聚力的最大間隙為

(6)

(7)

式中δc——顆粒間具有非凝聚力時的法向最大間隙，m

αc——2個顆粒的接觸半徑，m

當顆粒并非實際接觸并且間隙小于δc時，凝聚力達到最大值

(8)

摩擦力的計算和Hertz-Mindlin(no slip)接觸模型不同，其取決于JKR法向力的正向排斥部分。因此，該模型在接觸力的凝聚力分量更大時提供一個更大的摩擦力。

因此，經過處理后的廄肥具有散粒體的物料特性，廄肥顆粒之間受水分子和化學物質的影響也具有粘結力特性。為了更準確地模擬廄肥的真實狀態，本文選擇Hertz-Mindlin with JKR Cohesion 模型進行仿真模擬。

2.2 幾何模型建立

在仿真過程中，顆粒和裝置模型對仿真結果有很大的影響，在保證仿真模型尺寸與物理模型一致的基礎上，建立了簡化的廄肥和漏斗裝置模型。經過粉碎處理的散體廄肥顆粒近似球形，將廄肥顆粒模型設置為球形。在SolidWorks軟件中根據物理試驗模型建立仿真模型，把模型轉換為STL格式，導入EDEM 2.7軟件中作為漏斗裝置仿真模型，本文采用EDEM軟件內置的Hertz-Mindlin(no slip)接觸模型作為顆粒與裝置之間的接觸模型，顆粒模型及漏斗模型如圖2、3所示。

2.3 仿真參數設置

根據試驗所測定的廄肥顆粒粒徑分布范圍，為確保仿真結果準確性的同時提高仿真效率，僅生成粒徑分布占比較大區間的顆粒。在EDEM中采用隨機分布，將生成的球顆粒半徑限制在0.5～1.25倍的初始球半徑之間。仿真中，動態生成漏斗中顆粒，在漏斗正上方建立顆粒工廠，設置為虛擬，生成總質量為0.6 kg，生成速率為0.2 kg/s，數據保存時間間隔為0.01 s，固定時間步長是瑞利時間步長的20%，網格尺寸取2倍最小球形單元尺寸。基于EDEM內嵌Hertz-Mindlin with JKR Cohesion模型進行廄肥接觸參數的仿真標定，其模型參數(JKR表面能)是表征所研究物料含水率效果的重要參數。通過大量預試驗確定了JKR表面能的取值范圍。綜合對比文獻[12,18-20]中所研究肥料、土壤與本文所研究廄肥特性的差異，確定廄肥仿真接觸參數的取值范圍，如表3所示。

表3 仿真參數取值范圍Tab.3 Simulation parameters

2.4 仿真試驗與結果分析

2.4.1Plackett-Burman篩選試驗

Plackett-Burman篩選試驗通過考察目標響應與各因子間的關系，比較各個因子2水平間的差異性來確定因子顯著性。本文Plackett-Burman試驗設計以廄肥堆積角為響應值，對仿真接觸參數及接觸模型參數進行篩選。試驗接觸參數高水平設置為低水平的2倍，根據文獻[13-14]中因素高低水平取值方法，確定本文因素水平如表4所示。

表4 因素水平Tab.4 Factors and levels

Plackett-Burman試驗方案及結果如表5所示，A～G為因素水平值，H～L為空白列，利用Design-Expert 8.0.6軟件[27-28]對該結果進行方差分析，得到接觸參數和接觸模型參數顯著性如表6所示。由表6可知，JKR表面能、廄肥-廄肥恢復系數、廄肥-鋼恢復系數的P<0.05，對廄肥堆積角的影響顯著；而其他參數的P>0.05，對廄肥堆積角影響不顯著。

表5 Plackett-Burman試驗方案及結果Tab.5 Scheme and results of Plackett-Burman test

表6 Plackett-Burman試驗結果顯著性分析Tab.6 Significance analysis of Plackett-Burman test results

為方便后續試驗，在Box-Behnken試驗[29-30]中只考慮3個影響顯著的參數，不顯著因素取值分別為廄肥-廄肥靜摩擦因數0.65、廄肥-廄肥滾動摩擦因數0.3、廄肥-鋼靜摩擦因數0.53、廄肥-鋼滾動摩擦因數0.3，進行響應面試驗設計。

2.4.2Box-Behnken響應面試驗及回歸模型

根據響應面設計原理，選取顯著性參數的低、中、高3個水平進行試驗設計，試驗選取5個中心點對誤差進行評估。Box-Behnken試驗參數取值如表7所示。

表7 Box-Behnken試驗參數取值Tab.7 Parameter value of Box-Behnken test

Box-Behnken試驗方案及結果如表8所示，重點考察3個對廄肥堆積角影響顯著參數，即JKR表面能、廄肥-廄肥恢復系數、廄肥-鋼恢復系數。應用Design-Expert軟件建立堆積角θ與3個顯著性參數的二階回歸方程為

θ=30.92+1.75A+0.88D+3.23G-0.21AD- 1.07AG+0.46DG-0.63A2+0.041D2+0.69G2

(9)

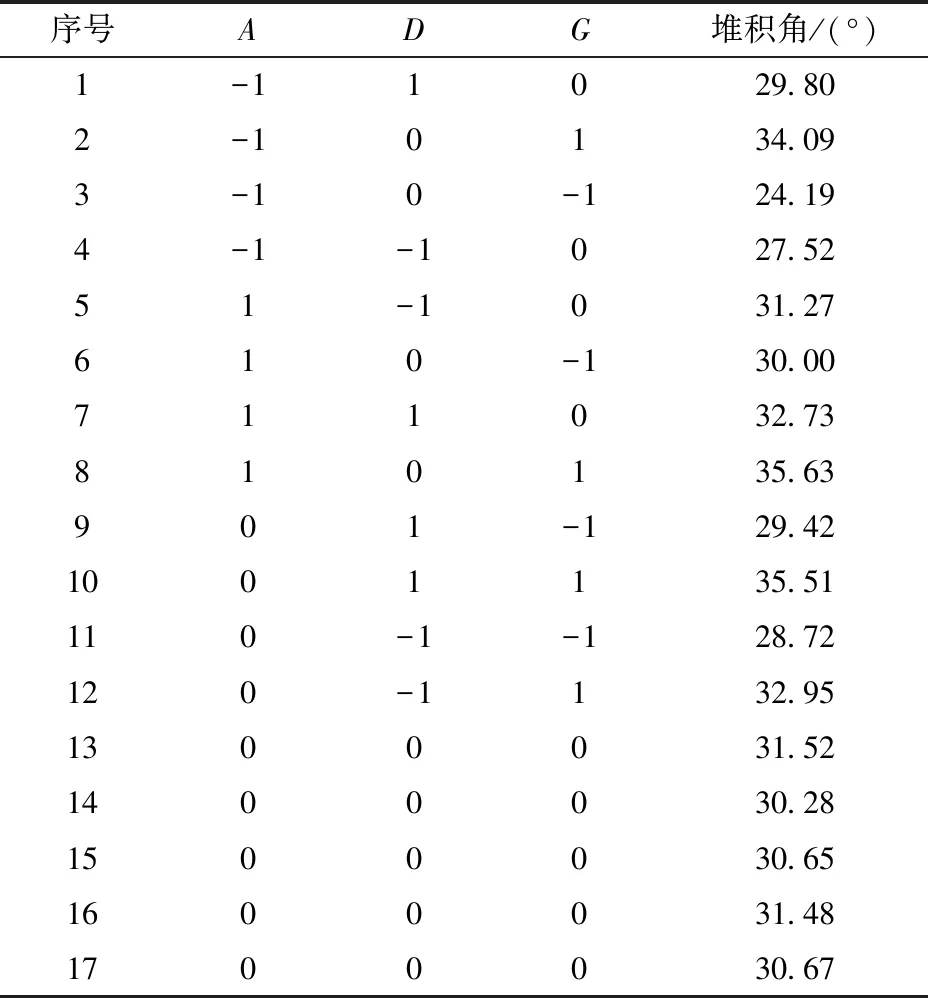
表8 Box-Behnken試驗方案及結果Tab.8 Design and results of Box-Behnken test

Box-Behnken試驗模型方差分析結果如表9所示，由表9可知，該擬合模型P=0.000 3，擬合度較好；廄肥-廄肥恢復系數(A)、JKR表面能(G)P值均小于0.01；廄肥-鋼恢復系數(D)、廄肥-廄肥恢復系數和JKR表面能交互項(AG)P值均小于0.05，說明各個參數對堆積角的影響顯著，表明回歸模型的有效性。失擬項P=0.114 7>0.05，表明所得回歸方程與實際擬合中非正常誤差所占比例小，沒有彎曲失擬現象發生，擬合性較好。試驗中變異系數為2.65%，說明試驗有較高的可靠性。決定系數為

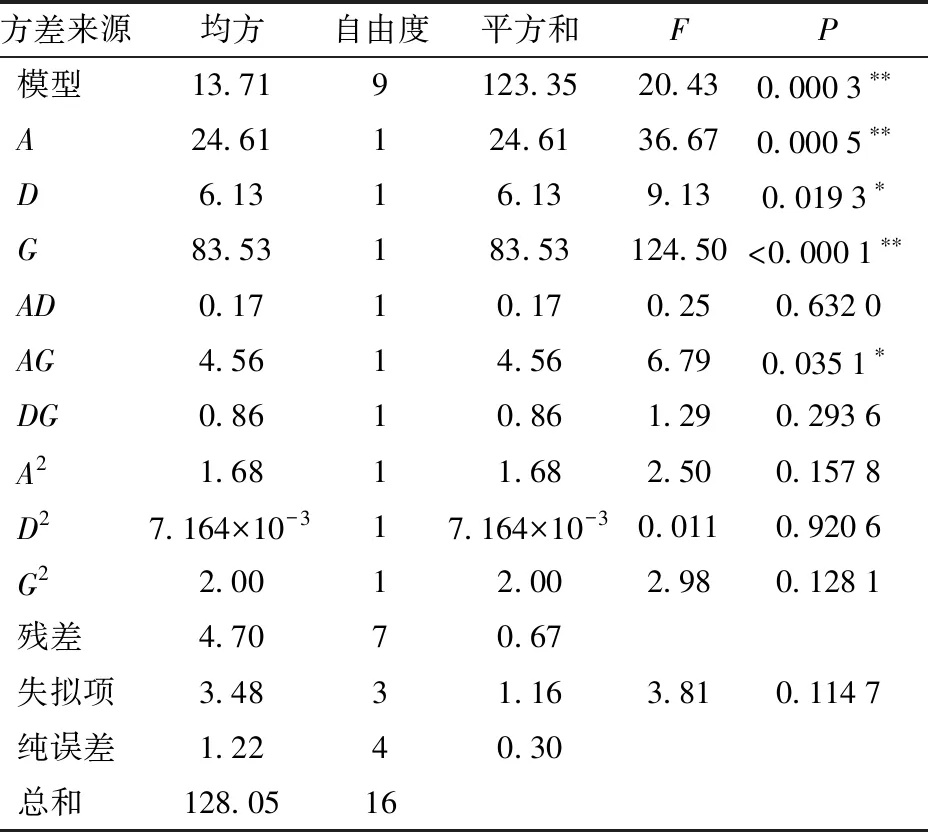
表9 Box-Behnken試驗模型方差分析Tab.9 ANOVA of quadratic polynomial model of Box-Behnken test

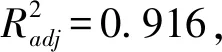
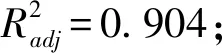
θ=30.97+1.75A+0.88D+3.23G-1.07AG

(10)

表10 Box-Behnken試驗優化回歸模型方差分析Tab.10 ANOVA of modified model of Box-Behnken test

2.4.3回歸模型交互效應分析

根據優化回歸模型方差分析結果，可知廄肥-廄肥恢復系數和JKR表面能的交互項(AG)對廄肥的堆積角影響顯著(P<0.05)。當廄肥-廄肥恢復系數為0.35時，應用Design-Expert軟件繪制廄肥-廄肥恢復系數和JKR表面能交互作用(AG)的響應曲面(圖4)，可以直觀地看出兩個參數之間的交互效應。由AG曲面可知，隨著兩個參數取值的增加，廄肥堆積角均呈現上升趨勢，相對于廄肥-廄肥恢復系數(A)，JKR表面能(G)的效應面曲線比較陡，表明其對堆積角影響較為顯著。

3 最佳參數組合確定與仿真驗證

應用Design-Expert軟件對優化后的回歸方程進行尋優求解，當JKR表面能為0.02 J/m2，廄肥-鋼恢復系數為0.49，廄肥-廄肥恢復系數為0.34，其余非顯著性參數選取中間水平(廄肥-廄肥靜摩擦因數0.65，廄肥-廄肥滾動摩擦因數0.3，廄肥-鋼靜摩擦因數0.53，廄肥-鋼滾動摩擦因數0.3)時，仿真結果與實際堆積角相對誤差最小。為驗證最優參數組合的準確性，采用上述參數值，其他參數設置不變，應用EDEM 2.7軟件進行堆積角仿真試驗，3次重復仿真所得廄肥堆積角分別為34.8°、35.0°、33.7°。廄肥堆積角3次平均值為34.5°。與廄肥實際堆積角35.47°的相對誤差為2.73%，并且，從圖5a可以直觀看出，利用標定后的廄肥參數得到的堆積邊界與廄肥物理試驗堆積結果比較接近，說明所得廄肥參數的最優值準確可靠，仿真試驗與物理試驗的對照如圖5b、5c所示。

4 結論

(1)通過Plackett-Burman篩選試驗，得到對廄肥堆積角具有顯著影響的接觸參數和接觸模型參數為廄肥-廄肥恢復系數、廄肥-鋼恢復系數、JKR表面能，而廄肥-廄肥的靜摩擦因數和滾動摩擦因數、廄肥-鋼的靜摩擦因數和滾動摩擦因數對堆積角無顯著性影響。

(2)通過Box-Behnken響應曲面試驗，得出對廄肥堆積角影響顯著的參數，建立顯著性參數與堆積角之間的二次回歸模型，并對其進行優化，根據其方差分析得出，3個顯著性參數的一次項(廄肥-廄肥恢復系數、廄肥-鋼恢復系數、JKR表面能、廄肥-廄肥恢復系數和廄肥表面能的交互項對廄肥堆積角影響顯著。

(3)通過對優化后的回歸模型求解可知，當JKR表面能為0.02 J/m2、廄肥-鋼恢復系數為0.49、廄肥-廄肥恢復系數為0.34，非顯著性參數選取中間水平時，仿真試驗和物理試驗得到的廄肥堆積角無顯著性差異(P>0.05)，說明采用響應面方法分析標定廄肥接觸參數和接觸模型參數可行。