精密光機(jī)系統(tǒng)多敏感軸裝配精度分析與裝配工藝優(yōu)化

吳 偉 鄧 準(zhǔn) 尚建忠 羅自榮 曹玉君

(1.國(guó)防科技大學(xué)智能科學(xué)學(xué)院， 長(zhǎng)沙 410073； 2.北京遙感設(shè)備研究所， 北京 100854；3.湖南交通工程學(xué)院高科技研究院， 衡陽(yáng) 421001)

0 引言

高性能精密光機(jī)系統(tǒng)已成為現(xiàn)代對(duì)地、空、海機(jī)動(dòng)探測(cè)與制導(dǎo)裝備中的核心部件，其設(shè)計(jì)和制造能力是衡量一個(gè)國(guó)家軍事和科學(xué)技術(shù)水平的重要標(biāo)志[1-3]。一直以來(lái)，這類光機(jī)系統(tǒng)的精密裝配受到國(guó)內(nèi)外眾多學(xué)者、研究機(jī)構(gòu)的關(guān)注[4-9]。作為一種復(fù)雜且高精度的精密光機(jī)產(chǎn)品，它包含多個(gè)敏感軸線，如光軸、慣導(dǎo)軸、機(jī)械軸等，這些敏感軸線之間的方向和位置精度對(duì)正確計(jì)算目標(biāo)位置的影響極大，其匹配精度是影響精密光機(jī)系統(tǒng)控制性能(跟蹤精度、穩(wěn)定精度)的關(guān)鍵環(huán)節(jié)之一。確保各敏感軸之間的裝配精度及裝配效率對(duì)精密光機(jī)系統(tǒng)的裝配一致性、性能穩(wěn)定性及系統(tǒng)可靠性具有重要意義。

由于涉及領(lǐng)域的特殊性，關(guān)于精密光機(jī)系統(tǒng)多敏感軸裝配的研究較少。李芳玲[10]針對(duì)某型航天器裝配過(guò)程中光學(xué)艙與彈軸的匹配問(wèn)題，設(shè)計(jì)了同軸工裝，以保證二者的同軸度；YANG等[11]針對(duì)回轉(zhuǎn)體對(duì)接中軸線對(duì)準(zhǔn)問(wèn)題，對(duì)圓柱形零件對(duì)接過(guò)程中的誤差傳播控制進(jìn)行了深入研究；HUSSAIN等[12]研究了Straight-Build Assembly方法，基于剛體運(yùn)動(dòng)模型建立了裝配過(guò)程的誤差傳播模型，并提出了3種優(yōu)化方法，結(jié)果表明，通過(guò)優(yōu)化可以使誤差降低40%左右；在裝配過(guò)程中，針對(duì)加工誤差和裝配誤差在各個(gè)工序間的累積傳播，SHIU等[13]基于關(guān)鍵產(chǎn)品特性和關(guān)鍵控制特性建立了裝配過(guò)程的誤差流模型，該模型考慮了產(chǎn)品幾何尺寸誤差，為多工位裝配過(guò)程建模奠定了基礎(chǔ)；WHITNEY等[14-15]將裝配過(guò)程看作離散事件，采用狀態(tài)轉(zhuǎn)換方程表示該離散系統(tǒng)，研究了裝配過(guò)程建模與控制理論的關(guān)系；楊勇等[16]提出一種基于結(jié)構(gòu)整機(jī)性能映射模型的薄弱件結(jié)構(gòu)優(yōu)化方法，通過(guò)改進(jìn)關(guān)鍵構(gòu)件提升了整機(jī)性能；劉檢華[17]針對(duì)航天器的裝配提出了一種集精度、物理特性及結(jié)構(gòu)件仿真分析一體化的虛擬裝配過(guò)程建模與仿真方法。

目前，在精密光機(jī)系統(tǒng)的多敏感軸裝配過(guò)程中大多采用直接對(duì)接法，該方法主要依賴于技師經(jīng)驗(yàn)，裝配一次性合格率較低，需要反復(fù)進(jìn)行修配和調(diào)整，這嚴(yán)重制約了該類產(chǎn)品的裝配質(zhì)量和裝配效率。本文以某型裝備為研究對(duì)象，對(duì)多敏感軸裝配精度進(jìn)行建模分析，研究零件加工誤差與軸線匹配精度的分布規(guī)律，通過(guò)調(diào)整裝配策略和優(yōu)化裝配工藝，以期保證各軸線之間的裝配精度指標(biāo)。

1 問(wèn)題描述與抽象

1.1 問(wèn)題描述

某型裝備采用異面共軸捷聯(lián)布局，如圖1所示，導(dǎo)引艙和慣導(dǎo)與彈體固連，二者安裝面不同，但光學(xué)系統(tǒng)視線軸、慣導(dǎo)X軸與彈軸共線。這種布局方式能夠有效減少?gòu)楏w彈性振動(dòng)引起的慣導(dǎo)軸與光軸轉(zhuǎn)角的不一致性[18]。

如圖2所示，理想情況下目標(biāo)在慣性空間的視線角q0為

q0=δ+ψ

(1)

式中δ——理想彈體坐標(biāo)系與基準(zhǔn)系X軸夾角

ψ——理想光軸與理想彈體坐標(biāo)系X軸夾角

在實(shí)際中，慣導(dǎo)和導(dǎo)引艙裝配過(guò)程中會(huì)存在誤差，慣導(dǎo)測(cè)量實(shí)際彈體坐標(biāo)系(X′MY′MZ′M)偏離理想彈體坐標(biāo)系(XMYMZM)，二者X軸夾角為Δδ；導(dǎo)引艙光軸實(shí)際測(cè)量坐標(biāo)系(X′SY′SZ′S)也會(huì)偏離彈體坐標(biāo)系，X軸偏離角為Δψ，此時(shí)，慣性空間下的目標(biāo)視線角q為

q=q0+Δq=δ+ψ+Δδ+Δψ

(2)

可知，裝配誤差會(huì)引起附加視線角[19]。為了保證系統(tǒng)的性能，在對(duì)該類裝備的裝配過(guò)程中，必須保證光軸、慣導(dǎo)軸和彈軸的X軸互相平行，并且任意兩軸之間的夾角在3′以內(nèi)的指標(biāo)要求。

1.2 問(wèn)題抽象

彈軸X向定義為圖1中基準(zhǔn)面的法線；慣導(dǎo)軸X向定義為慣導(dǎo)4個(gè)減振座安裝面最小二乘擬合面的法線；導(dǎo)引艙的光軸在裝配時(shí)無(wú)法測(cè)量，裝配時(shí)采用的也不是實(shí)際光軸，光學(xué)系統(tǒng)與伺服機(jī)構(gòu)的對(duì)接面是光學(xué)系統(tǒng)的基準(zhǔn)面，裝配時(shí)將光軸等效為此面的法線方向，光學(xué)系統(tǒng)自身裝調(diào)完畢后，通過(guò)研磨基準(zhǔn)面以保證其法線精度。

多敏感軸裝配相關(guān)部件的連接關(guān)系如圖3所示，帶箭頭虛線表示二者存在X向角偏精度要求，實(shí)線表示二者對(duì)接，所有對(duì)接部件的X軸方向均為對(duì)接面法線。

所有部件均可簡(jiǎn)化為圓柱形艙體，艙體對(duì)稱軸線為X方向，該多敏感軸裝配精度問(wèn)題就抽象為一系列艙段對(duì)接，保證其中若干艙體之間的角偏小于指標(biāo)要求即可。

2 多敏感軸裝配精度分析

2.1 角偏誤差累積模型

在每個(gè)艙段上下表面均建立坐標(biāo)系，坐標(biāo)系原點(diǎn)位于回轉(zhuǎn)軸上，當(dāng)艙體不存在加工誤差時(shí)，上下表面的坐標(biāo)系X、Y、Z軸互相平行，如圖4所示。

記某一艙體底面坐標(biāo)系為F，頂面坐標(biāo)系為F′。由于加工誤差的存在，艙體頂面和底面不平行，F(xiàn)′與F的對(duì)應(yīng)坐標(biāo)軸不平行。F′相對(duì)于F的旋轉(zhuǎn)誤差定義為(Δα,Δβ,Δγ)，分別表示F′繞坐標(biāo)系F的Y、Z、X軸的旋轉(zhuǎn)角。由于只研究X向角偏，所以可令Δγ=0。由于坐標(biāo)系原點(diǎn)位置可以任意指定，所以F′變換為F的變換矩陣[20]可簡(jiǎn)化為3×3的旋轉(zhuǎn)變換矩陣，即

(3)

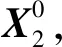
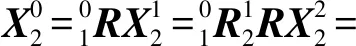
(4)

同理，當(dāng)有n個(gè)零件對(duì)接時(shí)，矢量Xn在坐標(biāo)系0中可表示為

(5)

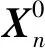
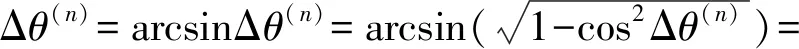
(6)

由于誤差Δαi、Δβi遠(yuǎn)小于1,簡(jiǎn)化式(6)可得

(7)

因此，可知最終角偏誤差Δθ(n)與每個(gè)對(duì)接艙段的加工誤差(Δαi,Δβi)都有關(guān)系，第i步裝配第i個(gè)零件而引入的誤差會(huì)在裝配的后續(xù)階段中累積。但誤差的累積并不一定是使角偏增大，若零件制造誤差符號(hào)相異，也可能得到較小的角偏，即艙段對(duì)接面的加工誤差之間存在補(bǔ)償關(guān)系。因此，根據(jù)式(7)可知，當(dāng)Δαi和Δβi的分布特征已知，可分析n個(gè)零件對(duì)接后角偏誤差Δθ(n)的裝配精度分布特征。當(dāng)n=1時(shí)，有

(8)

式中 Δθ(1)——某個(gè)艙段上下端面的角偏誤差

2.2 角偏誤差分布規(guī)律

雖然加工誤差Δα和Δβ與角偏誤差Δθ有直接聯(lián)系，但在設(shè)計(jì)和制造過(guò)程中并不直接對(duì)其提要求，而是規(guī)定艙段對(duì)接面的粗糙度、平面度以及相對(duì)于軸線的垂直度等形位公差。因此需要先根據(jù)裝配特征的形位公差研究Δθ的分布特征，再得出Δα和Δβ的分布。

實(shí)際艙體的對(duì)接面凹凸不平，假設(shè)上下對(duì)接面最小二乘擬合平面的法向與參考軸的夾角分別為Δγ1和Δγ2，它們是二維矢量。艙體上下對(duì)接面之間的角偏誤差為

Δθ=‖Δγ1+Δγ2‖

(9)

實(shí)際表面可看作不同頻率成分輪廓的疊加，包括粗糙度輪廓、波紋度輪廓和形狀誤差[21]。粗糙度屬于高頻微觀幾何誤差，波紋度是中頻介于微觀和宏觀之間的幾何誤差，形狀誤差屬于表面的低頻宏觀幾何誤差。艙段對(duì)接面采用磨削加工，波紋度幅值較小將其忽略，只考慮粗糙度和形狀誤差的影響。

為進(jìn)一步簡(jiǎn)化問(wèn)題，假設(shè)配合特征形狀誤差分量的波長(zhǎng)遠(yuǎn)大于特征尺寸。根據(jù)假設(shè)，形狀誤差分量的作用相當(dāng)于將粗糙度輪廓整體旋轉(zhuǎn)一定角度。某型裝備對(duì)接面粗糙度要求Ra=0.8 μm，平面度要求為0.01 mm。一般評(píng)價(jià)長(zhǎng)度內(nèi)最高波峰和最低峰谷之間的距離Ry≈8Ra=6.4 μm，可見(jiàn)零件平面度由粗糙度主導(dǎo)，形狀誤差中的短波長(zhǎng)分量幅值很小，可忽略。

因此推出‖Δγ‖的計(jì)算過(guò)程為：首先生成零件表面的粗糙度輪廓，然后將其在垂直度限制下繞Y或Z軸旋轉(zhuǎn)，最大的旋轉(zhuǎn)角即為所求。

3D粗糙輪廓的生成方法已經(jīng)比較成熟，包括Patir模型[22]、FFT法[23]、時(shí)間序列型[24]和分形模型[25]等，本文采用Patir模型生成3D粗糙輪廓，圖5為數(shù)值模擬粗糙度Ra=0.8 μm的粗糙表面。

為了驗(yàn)證粗糙表面生成的有效性，對(duì)比仿真表面與實(shí)測(cè)表面的平面度。實(shí)際測(cè)量了33個(gè)對(duì)接面樣本的平面度；運(yùn)行粗糙表面生成程序2 000次，并計(jì)算仿真表面平面度，其結(jié)果如圖6所示。圖6a為根據(jù)粗糙表面生成程序得到表面的平面度，圖中曲線為正態(tài)分布N(0.004 7,0.000 4)；圖6b為實(shí)測(cè)表面平面度，圖中曲線為正態(tài)分布N(0.004 6,0.001 6)。顯然，仿真表面與真實(shí)表面平面度具有相似的分布規(guī)律，但是由于實(shí)際表面在加工中受到更多因素的影響，因此其平面度的分布更加分散。

根據(jù)前面分析可知，疊加形狀誤差的過(guò)程相當(dāng)于在垂直度的限制下對(duì)粗糙度輪廓繞Y軸或Z軸進(jìn)行最大程度的旋轉(zhuǎn)，旋轉(zhuǎn)角為‖Δγ‖。零件垂直度的實(shí)際值為隨機(jī)變量，設(shè)上下對(duì)接面參考面位置分別為x1和x2，則垂直度p為

p=|x1-x2|

(10)

假設(shè)x1和x2服從正態(tài)分布x1～N(μ1,σ1)，x2～N(μ2,σ2)，則垂直度p符合折疊正態(tài)分布，其概率密度函數(shù)為

(11)

繪制實(shí)測(cè)的53個(gè)對(duì)接面的垂直度數(shù)據(jù)樣本的分布，如圖7所示，圖中曲線為折疊正態(tài)分布FN(0.015,0.006)。

依據(jù)圖7概率密度函數(shù)，隨機(jī)生成垂直度，然后對(duì)粗糙度輪廓繞Y軸進(jìn)行最大程度旋轉(zhuǎn)，得到‖Δγ‖分布規(guī)律如圖8所示，它符合廣義極值分布。在垂直度范圍內(nèi)，粗糙度輪廓可能的旋轉(zhuǎn)角是隨機(jī)的，而‖Δγ‖正是這個(gè)隨機(jī)樣本中的極大值，所以它符合極值分布，有

‖Δγ‖～GEV(μGEV=0.315 4,σGEV=0.197 3,ξGEV=-0.211 5)

(12)

式中μGEV——定位參數(shù)σGEV——尺度參數(shù)

ξGEV——形狀參數(shù)

如圖9所示，Δγ1和Δγ2是二維矢量，可以將其分解為繞Y軸轉(zhuǎn)動(dòng)和繞Z軸轉(zhuǎn)動(dòng)，根據(jù)式(9)可得

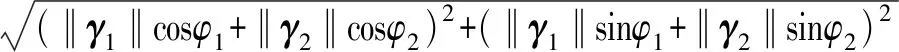
(13)

φ1和φ2符合0～2π內(nèi)的均勻分布，對(duì)式(13)進(jìn)行蒙特卡洛仿真，繪制仿真結(jié)果分布如圖10所示，分析得到Δθ符合萊斯(Rice)分布，即

Δθ～Rice(vR=0,σR=0.441 6)

(14)

萊斯分布概率密度函數(shù)為

(15)

式中I0——修正的0階第一類貝塞爾函數(shù)

假設(shè)Δα和Δβ獨(dú)立同分布，則根據(jù)式(8)以及萊斯分布的定義可知Δα和Δβ符合均值為0，標(biāo)準(zhǔn)差為σR的正態(tài)分布N(0,σR)。

通過(guò)上述仿真和分析，得到艙體對(duì)接面的加工誤差Δα和Δβ符合正態(tài)分布，艙體上下表面之間的角偏誤差Δθ符合萊斯分布。

3 基于裝配方向調(diào)整的逐工序優(yōu)化法

針對(duì)多艙段裝配問(wèn)題，將n個(gè)艙段對(duì)接過(guò)程分為n個(gè)工序，每個(gè)工序?qū)右粋€(gè)艙段。為了提高裝配精度，每個(gè)工序都應(yīng)該對(duì)角偏進(jìn)行控制，控制方法不同，最終得到的裝配精度也不同。對(duì)于回轉(zhuǎn)對(duì)稱艙段，設(shè)每個(gè)對(duì)接面有k個(gè)螺栓連接孔，在裝配過(guò)程中可以將艙段繞其回轉(zhuǎn)軸旋轉(zhuǎn)，從而每個(gè)艙段擁有k個(gè)可能的裝配方向。

3.1 直接對(duì)接法

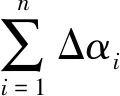
(16)

角偏均值(Mean)和標(biāo)準(zhǔn)差(Standard deviation, SD)分別為

(17)

(18)

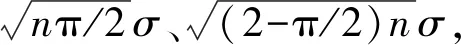
3.2 逐工序優(yōu)化裝配方向法

根據(jù)多艙段的裝配特點(diǎn)，提出了基于裝配方向調(diào)整的逐工序優(yōu)化法。 這種方法的本質(zhì)是在每個(gè)工序(Stage)中都盡量使角偏誤差Δθ(i)最小，第i個(gè)工序最優(yōu)化的方法是將艙段i繞其回轉(zhuǎn)軸旋轉(zhuǎn)，在k個(gè)可行的裝配方向中選取使Δθ(i)最小的方向進(jìn)行裝配。因此，工序i最終的角偏誤差Δθ(i)為

(19)

顯然Δθ(i)服從GEV分布，其母分布為Rice分布。

當(dāng)艙段螺釘孔個(gè)數(shù)k=6時(shí)，角偏的分布參數(shù)μGEV、σGEV、ξGEV與艙段加工誤差分布參數(shù)μN(yùn)、σN的關(guān)系如圖11所示。由圖11可知，當(dāng)σN≥0.7μN(yùn)時(shí)，角偏的分布參數(shù)幾乎不隨工序發(fā)生改變(除工序?yàn)?時(shí))。即當(dāng)制造誤差滿足σN≥0.7μN(yùn)，n個(gè)(n>2)零件對(duì)接，都將得到幾乎相同的角偏分布；當(dāng)σN<0.7μN(yùn)時(shí)，角偏的分布參數(shù)隨工序發(fā)生波動(dòng)。而且定位參數(shù)μGEV和尺度參數(shù)σGEV都是當(dāng)工序?yàn)榕紨?shù)時(shí)較工序?yàn)槠鏀?shù)時(shí)小。所以偶數(shù)個(gè)零件對(duì)接會(huì)比奇數(shù)個(gè)零件對(duì)接的角偏精度高。

采用這種裝配方法需要對(duì)現(xiàn)有加工和裝配工序進(jìn)行優(yōu)化調(diào)整，優(yōu)化后裝配工藝路線如圖12所示。

制導(dǎo)艙和動(dòng)力艙完成端面精加工后，暫不執(zhí)行其他加工工序，直接進(jìn)入裝配工序。光學(xué)系統(tǒng)與伺服機(jī)構(gòu)有方向要求，二者直接對(duì)接；慣導(dǎo)與安裝板之間可通過(guò)減振座預(yù)緊力調(diào)整角偏，二者也直接對(duì)接；然后將導(dǎo)引艙組合與制導(dǎo)艙對(duì)接，通過(guò)調(diào)整制導(dǎo)艙方向，最小化導(dǎo)引艙與制導(dǎo)艙之間的角偏。將慣導(dǎo)組合對(duì)接至制導(dǎo)艙，慣導(dǎo)與導(dǎo)引艙也有方向要求，通過(guò)調(diào)整減振座預(yù)緊力最小化慣導(dǎo)與導(dǎo)引艙角偏。將動(dòng)力艙對(duì)接至制導(dǎo)艙，通過(guò)調(diào)整動(dòng)力艙方向最小化導(dǎo)引艙與彈軸角偏。標(biāo)記各組合裝配方向，拆卸，然后完成制導(dǎo)艙和動(dòng)力艙的剩余加工工序，最后按照標(biāo)記的方向?qū)⒏髋撝匦卵b配。

4 案例裝配分析

采用仿真的方法對(duì)兩種對(duì)接方法進(jìn)行對(duì)比分析，輸入的零件艙段分布數(shù)據(jù)分為兩組案例，如表1所示。

表1 艙段的分布參數(shù)Tab.1 Distribution parameters of cabin

案例1是實(shí)測(cè)了40個(gè)艙段的上下端面的角偏Δθ，得到其分布為Rice(0.1,0.7)，Δα和Δβ的分布為N(0.070 7,0.7)，因?yàn)閷?shí)際艙段在加工過(guò)程中存在夾具誤差，所以Δα和Δβ的均值不為0；案例2中Δα和Δβ分別賦值為N(1,0.418 8)，則有Δθ～Rice(1.414,0.418 8)。

使用上述兩種方法分別對(duì)兩個(gè)案例進(jìn)行裝配，二者均包括8個(gè)艙段、6個(gè)螺釘孔，分為8個(gè)工序進(jìn)行裝配，不考慮裝配過(guò)程中的定位誤差和測(cè)量誤差，每個(gè)裝配實(shí)例仿真10 000次。

圖13為采用直接對(duì)接法的仿真結(jié)果。由圖可知，角偏均值、標(biāo)準(zhǔn)差隨工序增大而增加。艙段加工誤差μN(yùn)越大，則角偏均值增長(zhǎng)速度越大；σN越大，角偏標(biāo)準(zhǔn)差增長(zhǎng)速度越大。案例1中8個(gè)艙段對(duì)接后，角偏增大203.3%；案例2中8個(gè)艙段對(duì)接后角偏增大673.9%。

圖14為采用逐工序優(yōu)化裝配方向法的仿真結(jié)果。由圖可知，案例1與案例2角偏均值呈現(xiàn)出不同的特征，案例1對(duì)接后(工序大于1)角偏均值基本保持不變；案例2角偏均值則表現(xiàn)明顯的振蕩，工序?yàn)槠鏀?shù)時(shí)角偏均值處于波峰，當(dāng)工序?yàn)榕紨?shù)時(shí)角偏均值處于波谷，并隨著工序的增加逐漸收斂。相同的特征也體現(xiàn)在標(biāo)準(zhǔn)差上。因?yàn)榘咐?中σN≥0.7μN(yùn)，角偏分布參數(shù)基本不隨工序變化；而案例2中σN<0.7μN(yùn)，角偏的分布參數(shù)隨工序有規(guī)律的波動(dòng)。裝配后角偏明顯小于單個(gè)艙段的角偏，零件角偏越大，裝配后角偏也越大。案例1標(biāo)準(zhǔn)差小于案例2標(biāo)準(zhǔn)差，說(shuō)明裝配后角偏標(biāo)準(zhǔn)差不僅與加工誤差標(biāo)準(zhǔn)差有關(guān)，還與加工誤差均值有關(guān)。

圖15為采用兩種方法對(duì)接裝配時(shí)，不同工序角偏的概率密度分布圖。由圖15a可知，加工質(zhì)量、對(duì)接艙段個(gè)數(shù)對(duì)直接對(duì)接法裝配精度的影響都很大，不利于多段艙體對(duì)接裝配，角偏隨艙體個(gè)數(shù)增加而增加，且加工精度越低增速越大。如果以3′為指標(biāo)，一次性裝配合格率要求大于95%時(shí)，那么案例1對(duì)接零件個(gè)數(shù)不能超過(guò)3個(gè)，而案例2幾乎無(wú)法達(dá)到合格率要求。某型裝備艙體對(duì)接采用直接對(duì)接法，因?yàn)榕擉w對(duì)接前，內(nèi)部設(shè)備已經(jīng)安裝到位，設(shè)備具有方向性，致使艙體在對(duì)接時(shí)已經(jīng)無(wú)法調(diào)整方向。正因如此，其裝配一次合格率非常低，經(jīng)常要“測(cè)試-拆卸-修配-裝配-測(cè)試”6～8次，甚至出現(xiàn)過(guò)反復(fù)20余次的極端情況。

由圖15b可知，逐工序優(yōu)化裝配方向法對(duì)艙段加工誤差具有較明顯的補(bǔ)償能力，對(duì)接艙體個(gè)數(shù)的增加對(duì)降低最終角偏并無(wú)明顯作用。案例1中8個(gè)艙體對(duì)接的角偏相對(duì)于2個(gè)艙體對(duì)接的角偏僅下降3%。案例2中對(duì)接艙體達(dá)到4個(gè)后，角偏波動(dòng)趨于平穩(wěn)，8個(gè)艙體對(duì)接角偏相對(duì)于4個(gè)艙體對(duì)接角偏變動(dòng)5%，并且兩個(gè)案例裝配后角偏小于3′的概率大于99.8%。

5 結(jié)束語(yǔ)

以某型裝備為研究對(duì)象，分析了光軸、慣導(dǎo)軸與機(jī)械軸等多敏感軸之間的裝配精度。通過(guò)研究該類裝備的裝配結(jié)構(gòu)特點(diǎn)，將多敏感軸精度裝配問(wèn)題抽象為艙段對(duì)接過(guò)程中的角偏精度問(wèn)題，基于坐標(biāo)變換建立了多敏感軸裝配過(guò)程的角偏誤差累積模型，提出基于粗糙表面研究不同對(duì)接方法下角偏概率分布的方法，分別對(duì)采用傳統(tǒng)的直接對(duì)接法和所提出的逐工序優(yōu)化裝配方向法下的角偏概率分布規(guī)律進(jìn)行了研究，并對(duì)兩個(gè)設(shè)計(jì)案例進(jìn)行了仿真。研究表明，采用直接對(duì)接法時(shí)，艙段加工誤差在裝配過(guò)程中累積顯著，難以滿足各軸線之間3′的裝配精度指標(biāo)要求，也揭示了當(dāng)前裝配一次性合格率較低的原因。而逐工序優(yōu)化裝配方向法能夠在較大程度上補(bǔ)償艙段的加工誤差，并對(duì)當(dāng)前的精密裝配工藝進(jìn)行優(yōu)化，該方法能夠有效保證各敏感軸線之間的裝配精度，且裝配精度幾乎不受對(duì)接艙段個(gè)數(shù)的影響。