教材解讀：對數函數的概念

【摘 要】 對數函數新舊教材擦差異較大，要全面理解對數函數，要先分析新舊教材的差異，然后聚焦到“對數函數的概念”，最后思考面對新的變化我們的教學該怎么辦.

【關鍵詞】 教材解讀;教材比較;對數函數

對數函數是高中數學核心內容之一，也是高一學生學習難點之一，同時對數函數也是連接初等數學與高等數學的一個紐帶，因此理解對數函數、教好對數函數非常有必要.

在人教A版舊教材[1]（依據2003年版課程標準編寫的教材）中，對數函數安排在必修1第二章第二節（2.2.2對數函數及其性質），在新教材[2]（依據2017年版課程標準編寫的教材）中，對數函數安排在必修第一冊第四章第四節（4.4對數函數），都是高一學習的內容.新舊教材編寫差異較大，最顯著的差異是新教材“對數函數的概念”單獨成一節，筆者將對這一內容做出解讀，以便全面深入地理解對數函數這一核心內容.

1 “對數函數”新舊教材差異

對數函數新舊教材編寫差異，包括編寫理念、內容的安排、編寫的順序，素材的選取，例題習題的安排等，差異都很大.本文不面面俱到地研究這些差異，只從以下三個視角對兩者做一個比較，以點帶面，旨在幫助大家整體地理解對數函數.

1.1 教材編排：一節VS三節

在舊教材中，對數函數分為兩部分：“2.2.1對數與對數運算”和“2.2.2對數函數及其性質”，其中對數與對數運算對應新教材“4.3對數”（本文不研究這塊內容的比較）.“2.2.2對數函數及其性質”介紹了對數函數的概念，對數函數的圖象與性質.在它之后是冪函數.

在新教材中，“4.4對數函數”安排了三節：4.4.1對數函數的概念，4.4.2對數函數的圖象與性質，4.4.3不同函數的增長差異.

4.4.1對數函數的概念是新教材新增加的，也是本文將重點解讀的部分.

4.4.2對數函數及其性質，內容編寫與舊教材差別不大，都是先研究具體的函數y=log2x與y=log12x，并由此歸納出一般的對數函數的圖象與性質，然后是應用，最后介紹了指數函數y=ax與對數函數y=logax互為反函數.

4.4.3不同函數的增長差異，新舊教材都有，但差異很大.在舊教材中，它出現在3.2節，與對數函數不是在同一章.對幾種不同增長的函數模型的認識是與應用聯系在一起的，通過具體的實例，通過數學建模，體會各種模型的增長速度的快慢.在新教材中，是通過具體的函數y=2x與函數y=2x以及y=110x與y=lgx的比較，先感性認識各種模型的增長速度的快慢，再概括出相應的一類函數的增長快慢.新舊教材相比而言，筆者認為新教材更精簡，更符合學生的認知規律，更利于掌握不同函數的增長差異這一內容.

1.2 對數函數的概念：一段VS一節

新教材新增了一節“對數函數的概念”，這是占一個課時的內容，應引起了重視.

概念的引入，新舊教材利用的素材是相同的，都是“碳14衰減的例題”，但是兩者詳略程度是不可同日而語的.

舊教材在介紹對數函數概念時，只是用了一段話就引出了對數函數的概念，接著是探究對數函數的圖象與性質.

新教材在介紹對數函數概念時，用了一節內容，在呈現碳14衰減規律后，從圖象、表達式兩個角度進行分析，從而抽象出對數函數的概念.在揭示概念之后，安排了兩個例題，例題1是求函數的定義域，例題2是從指數和對數兩個角度解決物價增長問題.在這之后，才探討對數函數的圖象與性質.

1.3 內容核心：單核心VS雙核心

我們對概念的解構是為了確定概念的核心，確定概念的核心既要考慮數學內容本身，也要考慮學生的認知規律[3].從數學內容的知識體系看，對數的概念，圖象與性質都是重要的內容，都是對數函數這一內容的核心所在.在舊教材中，對數的概念以及圖象與性質，是在同一節課內進行的，教學時自然有所側重;從學生的認知看，他們接受這兩個內容也是有側重的，顯而易見，無論是教師還是學生都會把重點放在圖象與性質上.所以可以說，舊教材“對數函數”內容的核心實際上只有一個：圖象與性質.

而新教材就不同了，對數函數的概念單獨成節.所以“對數函數的概念”是內容的核心，而圖象與性質是理所當然的核心，所以，可以說新教材“對數函數”內容的核心有兩個：一是對數函數的概念，二是對數函數的圖象與性質.

新教材將內容確定為兩核心，強調了概念的獲得過程.在碳14衰減實例的基礎上，進一步對生物體死亡時間進行探究，通過演繹推理的方法得到生物體死亡時間與碳14含量的關系，進而抽象出對數函數的概念，關注了對學生數學抽象的核心素養的培養.

2 “對數函數的概念”逐段解讀

2.1 節引言

解讀 節引言有承前啟后的作用，它聚焦到學生的學習最近發展區，前面學習的指數函數模型以及對數，為后面學習對數函數做了數學上的準備.這里有一個提示作用，即將學習的內容與“函數”有關且與“對數”有關，是兩者結合的“對數函數”.

2.2 概念的獲得

解讀 數學課程標準指出：“數學源于對現實世界的抽象，基于抽象結構，通過符號運算、形式推理、模型構建等，理解和表達現實世界事物的本質、關系和規律” [4]，教材期望通過這一思考問題，提升對這段話的理解.對數函數與指數函數可以從不同的角度刻畫同一問題的變化規律，在碳14 的衰減問題中，死亡生物體碳14含量隨時間變化成指數衰減，這是上一節研究過的問題.教科書給出的思考是，已知死亡生物體內碳14含量求時間，這與前一節的問題是“互逆”的，這樣不僅可以引出對數函數的概念，而且揭示了對數函數與指數函數之間的聯系.

教科書沒有到此為止，而是進一步提出問題，死亡時間x是碳14含量y的函數嗎？這是用函數的觀點看問題，實際上只要是兩個變量之間有依賴關系，我們都要考慮他們之間的函數關系.

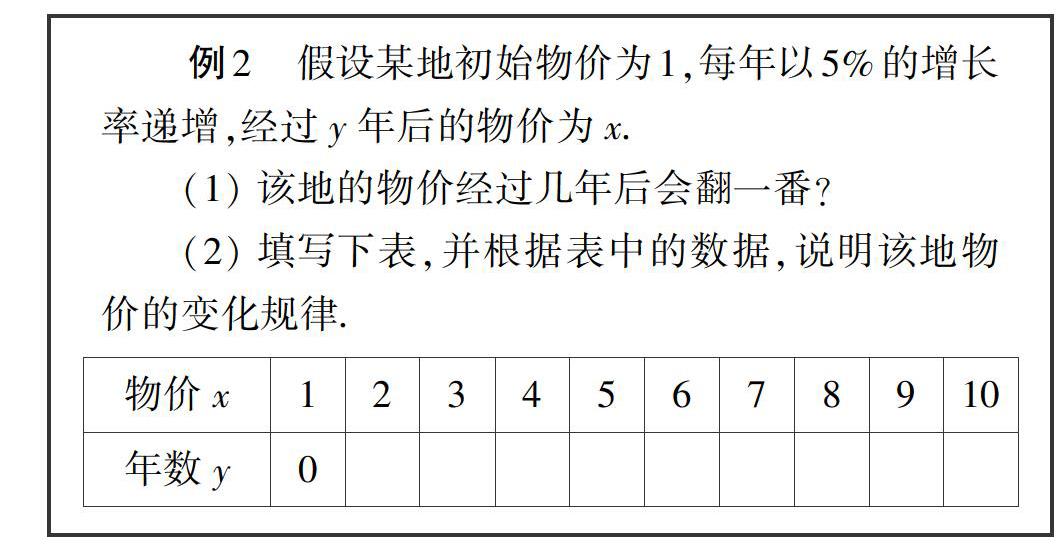
根據指數與對數的關系，由y=[SX（]1[]2[SX）][JB））][SX（]x[]5730[SX）]（x≥0）得到x=log[KF（S]5730[][SX（]1[]2[SX）][KF）]y（0

解讀 問題提出后，教材從圖和代數式兩個角度進行研究.圖是直觀的，代數式是形式化的，也是我們數學研究的最高追求.要研究出函數的表達式，也就是，要對定性的結果用定量的方式表達.

這里的圖是指數函數的圖，教學時教師可以給學生呈現這張圖，進而提出問題：

問題1：當碳14的含量為50%時，生物體死亡了多少年？

問題2：當碳14的含量為y0時，生物體死亡了多少年？

在學生求出x0=log573012y0后，請他們在圖中標出.

問題3：圖4.41中，x是否是y的函數？為什么？

學生回答“是”，需要他們用函數定義回答.

通過3個問題，不僅明晰了y∈（0，1）時，對應關系x=log573012y表示x是y的函數，而且該函數刻畫了時間x與碳14含量y的變化規律，很好地回答了思考的兩個問題.

同時，我們注意到對數函數的概念引出與指數函數是不同的，指數函數的概念是用歸納推理的方式得到，而對數函數是用演繹推理的方式得到.歸納、類比與演繹推理是“邏輯推理”核心素養的兩種表現形式，兩方面都不可偏頗.

同樣地，根據指數與對數的關系，由y=ax（a>0），且a≠1）可以得到x=logay（a>0，且a≠1），x與是y的函數.通常，我們用x表示自變量，y表示函數.為此，將x=logay（a>0，且a≠1）中的字母x和y對調，寫成y=logax（a>0，且a≠1）.

解讀 接著，由特殊到一般，由一般的指數函數y=ax得到x=logay.這里要讓學生再用函數的定義解釋：y>0，對應關系x=logay表示x是否是y的函數，以進一步理解函數的本質：即兩個數集之間的一種特殊的對應關系.指數函數的對應關系是f：x→ax，對數函數的對應關系是f：x→logax.

通常，我們用x表述自變量，用y表述函數，這是我們的習慣，為了研究方便，所以寫成對數式子后，將x和y對調.

另一個問題是，到這里“反函數”的概念呼之欲出，要不要順便講述？筆者認為，這時不應講反函數，原因有兩點，其一，我們研究問題要聚焦，我們的目標是引出對數函數的概念，而不是反函數;其二，如果這時講反函數的概念，從學生的認知角度看，反函數更有沖擊力，這樣反而弱化了對數函數的概念.

教材處理問題的線索是：直觀想象——形式表達——數學抽象.這是解決實際問題的需要，但是我們數學解決的是比實際問題需要更一般的函數，這也是挖掘內容的育人價值所在.

一般地，函數y=logax（a>0，且a≠1）叫做對數函數（logarithmic function），其中x的自變量，定義域是（0，+∞）.

解讀 抽象出對數函數的概念后，需要對概念進行辨別.概念教學通常有六個環節：情景問題——分析共性——抽象概念——概念辨析（內涵與外延的把握）——概念的表述——鞏固與應用（應用是分層次的，有直接的應用和有聯系應用）[5].對數函數與冪函數、指數函數一樣，都是形式化定義，形式化定義應關注其代數式結構.筆者認為，對形式化定義的概念的辨別要適可而止，不能將之當成教學的重點，比如“y=log2（2x+3）是不是對數函數？”這種辨別意義不大. 我們要將教學的重心放在函數的三要素上，用一般函數的概念指導具體一類函數的學習，即在一般函數概念的指導下，借助冪函數、指數函數的研究經驗，完成對對數函數的概念的抽象.

2.3 例題

例1 求下列函數的定義域：（1）y=log3x2;（2）y=loga（4-x）（a>0，且a≠1）.

解讀 例1求函數的定義域，這就是從函數的三要素上做文章，用一般的函數的概念指導具體一類函數的學習.

另一個問題是，如何講例題？教材主編章建躍先生曾提出：“例題教學不是簡單的教師示范，然后學生模仿.而是要引導學生‘分析題意、理解題意、你們干，我來看”，即教師要理解教材的意圖，通過引導學生分析題意，進而理解題意，分析清楚后讓學生自己動手去做.

例2 假設某地初始物價為1，每年以5%的增長率遞增，經過y年后的物價為x.（1）該地的物價經過幾年后會翻一番？（2）填寫下表，并根據表中的數據，說明該地物價的變化規律.

解讀 例2用對數函數的概念解決實際問題，從指數增長模型x=（1+5%）y得到對數函數y=log1.05x，蘊含了指數函數與對數函數的關系.同時，這里也隱含著不同增長函數模型的比較，這也是用聯系的觀點看問題.

另一個需要注意的是數學語言的表達，題中給出的是表格，如何從表格中看出規律？“物價隨時間的增長而增長”這句話學生能回答出來，但是后一句話“大約每增加1倍所需要的時間在逐漸縮小”，學生很難清晰的表達出來.

3.1 用聯系的觀點看問題

教學設計要瞻前顧后，就是要用聯系的觀點看問題.數學課程標準主題式的內容編排就是強調聯系，強調從整體上把握教學內容.實際上，新課程所提倡的單元教學設計，也是這個意思.

為了整體上把握對數函數的概念，教學時可以從兩個方面入手.

一是關注對數函數的內部聯系，即從整體上認識對數函數.對數函數的解析式、定義域、值域、圖象與性質等是一個有機的整體，教學時不可分割.

二是關注對數函數的外部聯系，即加強對數函數與指數函數的聯系.教科書是在研究了指數冪、指數函數、對數的表示與運算的基礎上研究對數函數的.引入對數函數的實例，也是學習指數函數的例子，這是從不同的角度看同一個問題，體現了聯系性.另外，在下一節內容不同增長函數模型的比較，也是用聯系的觀點看問題.3.2 用函數的觀點看問題

函數是高中數學的主線，在前面的學習中，學生對函數的思想有較多的感受，但是真正理解函數思想卻是一個漫長的過程[6]，這需要在平時教學中不斷的滲透.

就本節教學而言，讓學生學會用函數的觀點看問題，可以從三個方面入手：

其一，在提出思考問題“死亡時間x是碳14含量y的函數嗎？”后，從圖和解析式兩個角度說明x是y的函數，這里要求學生用函數的定義做出判斷，這是以一般函數的概念來指導具體函數的學習.

其二，例題1求定義域，是關注的函數的三要素，這是從不同的角度把握對數函數.

其三，教材中，對數函數的編排線索是“背景——概念——圖象和性質——應用”，我們在教學時應按照這一線索展開教學，應強調一般函數的研究套路.3.3 關注數學的語言表達

數學是一門語言，學好數學語言，用好數學語言是我們在教學中要下功夫的地方.本節而言，對數學語言的使用有兩處要特別關注：其一，在對數函數的概念引入時，從指數函數y=ax得到x=logay時，將x和y對調.這是為了研究方便，適合我們的習慣而采取的措施，這體現了語言使用的特點.其二，例題2的教學，從表格中的數據歸納變化規律時，對于數學的精確與實際問題的解決的表述，這種表述要求較高，在教學時應特別重視.如此才能真正感受數學是表達和交流的語言，引導學生用數學的語言表述世界.

參考文獻

[1] 劉邵學，章建躍等.普通高中教科書數學必修[M].北京：北人民教育出版社，2019.

[2] 章建躍等.普通高中教科書數學必修第一冊[M].北京：北人民教育出版社，2019.

[3] 朱成萬.中學數學核心內容的教學解構與建構[M].北京：中國經濟出版社，2015.

[4] 教育部.普通高中數學課程標準（2017年版）[M].北京：人民教育出版社，2018.

[5] 曹才翰，章建躍.中學數學教學概論（第二版）[M].北京：北京師范大學出版社，2008.

[6] 章建躍等.普通高中教科書數學必修第一冊（教師教學用書）[M].北京：北人民教育出版社，2019.

作者簡介 朱成萬（1973—），男，安徽太湖人，高級教師，人民教育出版社教材培訓專家，杭州市131培養人才，專著有《高中數學核心內容的教學解構與建構》，編著《至精至簡的高中數學思想與方法》，發表或獲獎論文90余篇，研究方向：數學教學.