密流比對壓氣機葉柵性能影響研究

馬亞男，周正貴

(南京航空航天大學 能源與動力學院，江蘇 南京 210016)

0 引言

壓氣機葉片氣動設計方法分為4個步驟[1-2]。其中二維葉型是構成三維葉片的基本元素，其氣動性能由S1流面(回轉面)二維葉柵流動決定。軸向速度密流比(axial velocity density ratio, AVDR)(以下簡稱密流比)定義為葉柵出口軸向密流與進口軸向密流之比，用來衡量壓氣機流道收縮程度。密流比是影響回轉面葉柵氣動性能的重要參數，文獻[3]針對高負荷可控擴散葉型，在0°攻角下、密流比在1.177～1.350范圍內，研究密流比對葉柵性能影響，結果表明：密流比增加，損失和壓升都會明顯下降。文獻[4]針對大轉角葉柵，研究了超臨界狀態葉柵性能隨密流比變化，結果也表明損失隨密流比增加而下降。在平面葉柵實驗中需要控制葉柵流場密流比，保持被試驗葉型構成葉柵的密流比與其在實際三維流動的一致性，這樣才能驗證葉型的真實氣動性能。在平面葉柵實驗中，可采用端壁面收斂，增大密流比[3]。減小密流比則需要控制端壁附面層發展，難度較大，比較有效的方法是進行附面層吸除，如王東等[5]采用端壁開槽進行端壁附面層抽吸。鄧熙等[6]指出，平面葉柵實驗中采用過大的抽吸量控制密流比將影響葉柵主流區域流動二維性。

本文首先對一個高壓比壓氣機轉子流動進行分析，驗證上、下環壁附面層處的勢流區流動呈回轉面二維特征。再針對超音轉子、高亞音轉子回轉面葉柵進行流場數值模擬和分析，研究密流比對壓氣機葉柵全工況氣動性能和流場影響，確定葉型對不同密流比的適用性，為二維葉型氣動設計提供參考。

1 回轉面二維流場計算方法

回轉面二維葉柵流場計算采用三維流場計算方法。如圖1所示，圖中1、2分別代表葉柵進口和出口截面。取一流片，上下回轉面設置成無黏邊界。

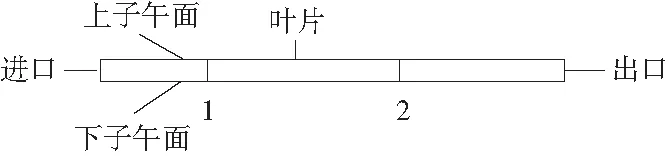
圖1 回轉面葉柵子午面流道視圖

軸向密流比AVDR：

式中：ρ1、ρ2、v1a、v2a分別為葉柵進、出口密度和軸向速度；δ1、δ2分別為葉柵進、出口流面厚度。本文通過改變進出口流面厚度比改變軸向密流比。

使用商用軟件NUMECA進行數值仿真。 S1流面網格類型為O4H，網格節點分布如圖2所示。

圖2 網格節點分布

流場計算進口給定總溫、總壓，軸向進氣，出口給定反壓。經過網格無關性驗證，對于超音和高亞音轉子葉柵均選擇網格量為50000進行研究。

2 軸流壓氣機葉片通道內流動二維特征分析

選取一高壓壓氣機轉子，分析軸流壓氣機轉子葉片通道內流動的回轉面二維特征。由設計點三維計算結果，在10%、50%、90%葉高處取進口流面厚度2 mm流片進行回轉面計算(圖3)。

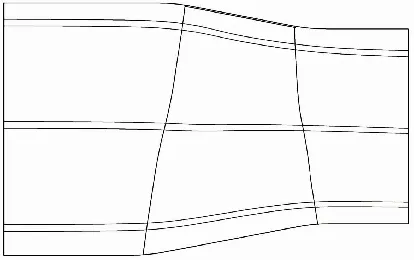
圖3 回轉面計算葉高位置

根據圖4、圖5，在10%、50%葉高，進出口馬赫數、激波位置、強度差異較小，整體一致性較好；90%葉高差異較大。圖6表明，10%和50%葉高流片厚度沿流向近似呈線性減薄；但90%葉高子午流道先收縮后擴張，在葉柵通道內形成喉道。圖4(f)表明，采用回轉面二維計算通道中氣流經正激波成為亞音氣流，后加速至超音(喉道處Ma=1)。而實際三維計算中90%葉高三維性較強，并沒有形成喉道，因此三維計算與回轉面計算差異較大。

將喉道附近子午面向上下兩邊外擴微調(圖5)，消除喉道。由圖4(a)、圖4(g)及圖6(c)可以看出：微調后(回轉面葉柵T)葉片通道內激波結構以及葉片表面壓力分布與三維流場一致性均變好。雖然在逆向分析時，回轉面二維流動與三維流動有較大差別，但在回轉面葉型設計時，通常采用流面厚度比沿流向線性變化，不會產生喉道。因此對于90%葉高進行回轉面葉型設計，應用于三維葉片是可行的。

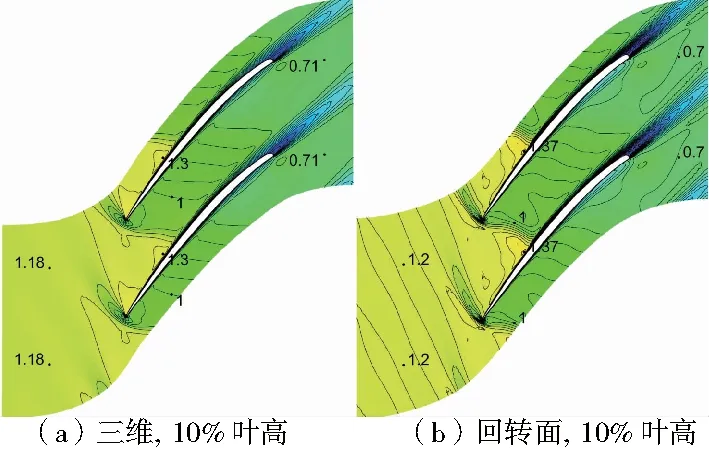
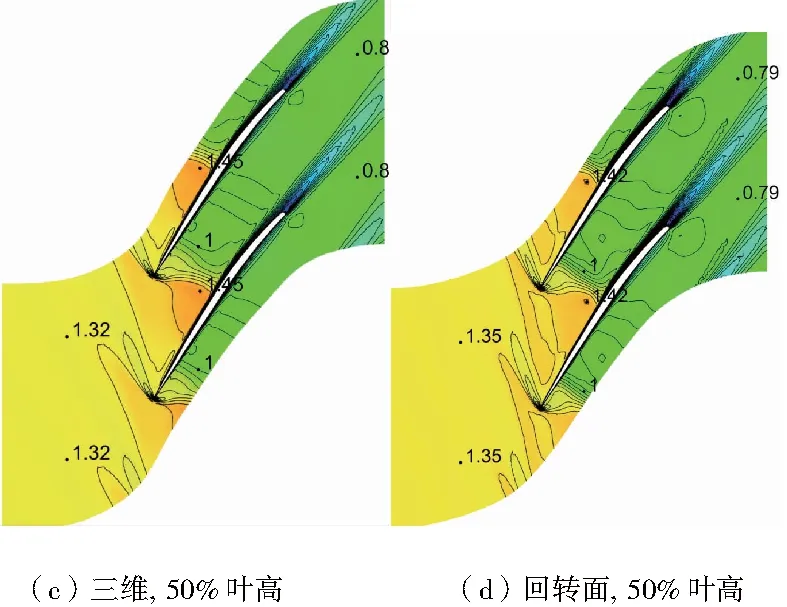
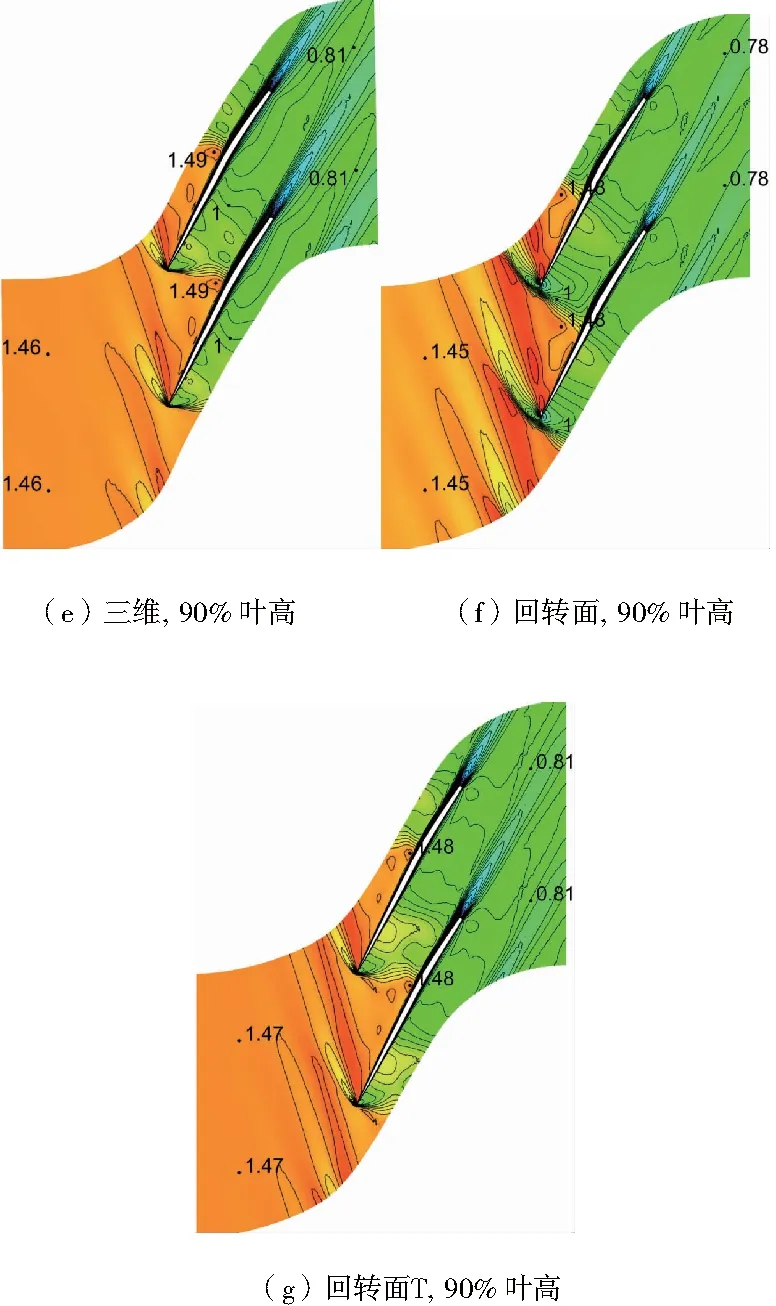
圖4 轉子三維和回轉面計算相對馬赫數等值線云圖

圖5 不同葉高子午流道相對厚度沿軸向位置分布

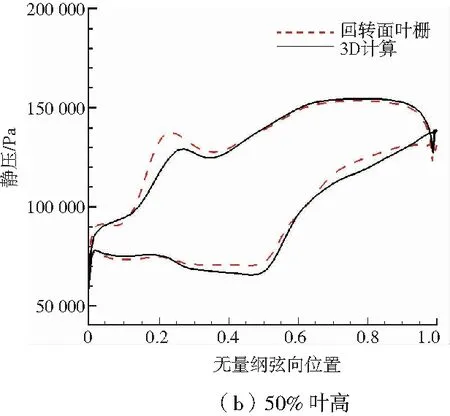
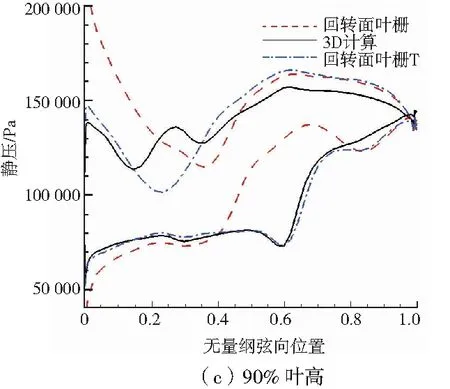
圖6 轉子三維和回轉面計算葉片表面壓力分布

3 密流比對壓氣機葉柵氣動性能影響研究

對超音轉子葉柵、高亞音轉子葉柵進行不同密流比影響研究，密流比分別為1.0、1.1、1.2、1.3。

3.1 超音轉子葉柵

由于超音葉柵流動具有唯一攻角特征，在此給出其壓比和效率隨出口反壓變化，以考察非設計工況性能。由圖7所示，密流比增大，超音葉柵總壓比和效率均增大；但耐反壓能力下降，因此會使對應的壓氣機裕度降低。

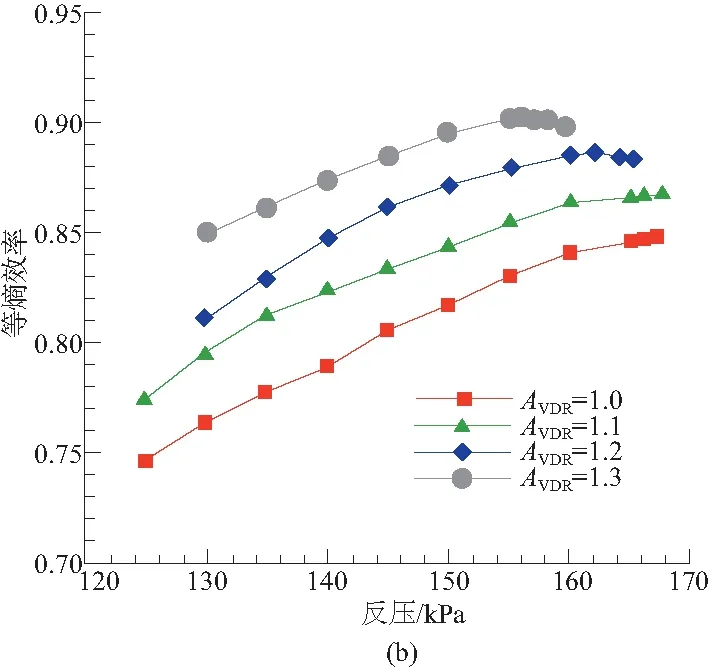
圖7 超音葉柵特性曲線

由圖8、圖9可知，隨著密流比增加，結尾正激波前移，葉柵耐反壓能力下降，葉片前緣載荷增大。

根據圖8、圖10，隨著密流比增加，超音葉柵尾緣附面層厚度逐漸減小。這是因為超音氣流通道收斂度增加，抑制正激波后亞音氣流減速增壓，葉片尾緣附面層厚度減小，附面層損失減小。密流比1.0～1.1時，正、斜激波前相對馬赫數均增大；1.1～1.3時減小，激波強度先增強后減弱。雖然密流比1.1時激波損失最高，但此時葉片尾緣附面層厚度較密流比1.0時明顯減小，因而激波和附面層造成的整體損失逐漸減小，效率升高。

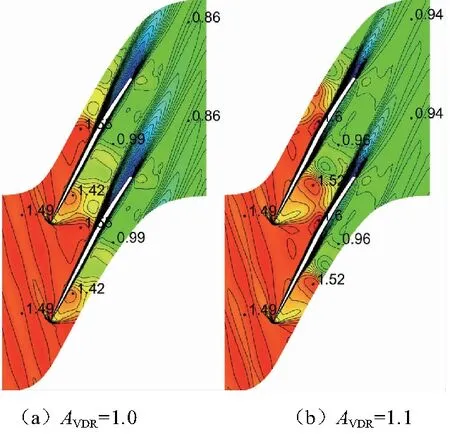
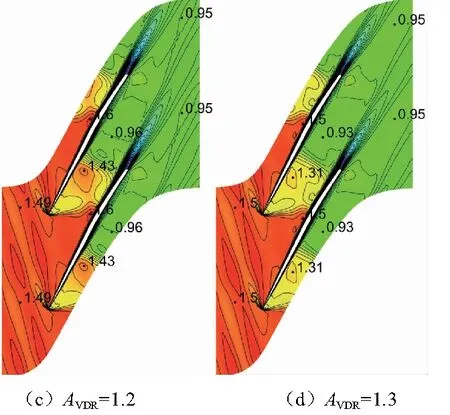
圖8 超音葉柵相對馬赫數等值線云圖

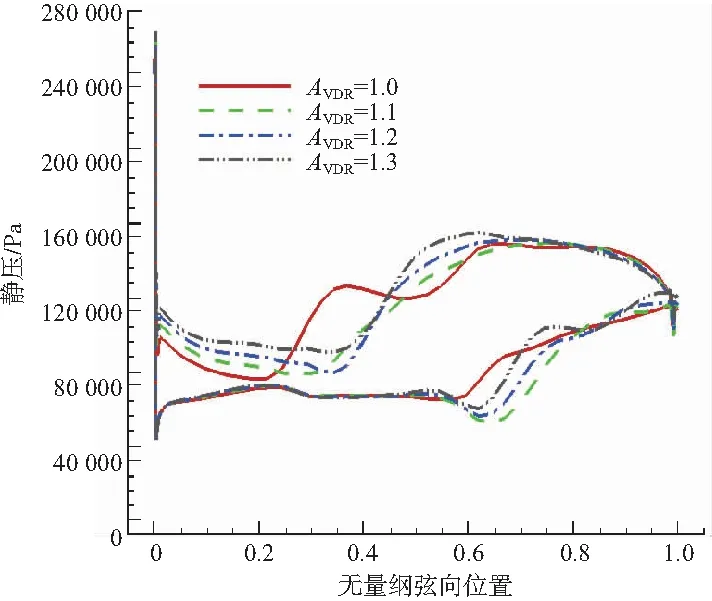
圖9 設計反壓下葉片表面壓力分布

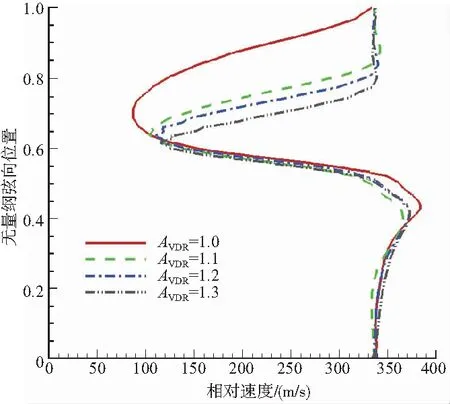
圖10 超音葉柵尾緣后10%軸向弦長相對速度沿切向分布

綜上，對于軸向亞音的進口平直段超音葉柵，隨著密流比增加，附面層厚度減小，落后角減小，氣流轉角增大，總壓比增大，效率升高；結尾正激波前移，葉柵耐反壓能力下降。

3.2 高亞音轉子葉柵

圖11為等馬赫數(Mw1=0.74)特性線。隨著密流比增加，氣流轉角增大(落后角減小)，負攻角總壓損失系數基本不變，正攻角總壓損失系數明顯下降，且低損失氣流角范圍向正攻角方向增加。這是因為密流比增加導致擴壓度減小，可延遲大攻角逆壓梯度分離(失速)。

圖11 高亞音轉子葉柵等馬赫數特性曲線

由圖12、圖13可知，在密流比1.0時，葉片尾緣附面層分離，損失較高。結合圖14，隨著密流比的增加，尾跡區高熵范圍減小，尾緣附面層厚度減小，落后角減小，氣流轉角增大，總壓損失系數減小，原因是通道收斂度增加，抑制氣流在通道內減速增壓，葉柵尾緣馬赫數增加。隨著密流比的增加，附面層厚度減小幅度降低，密流比較大時再增加密流比影響減小。

圖12 0°攻角高亞音轉子葉柵相對馬赫數等值線云圖

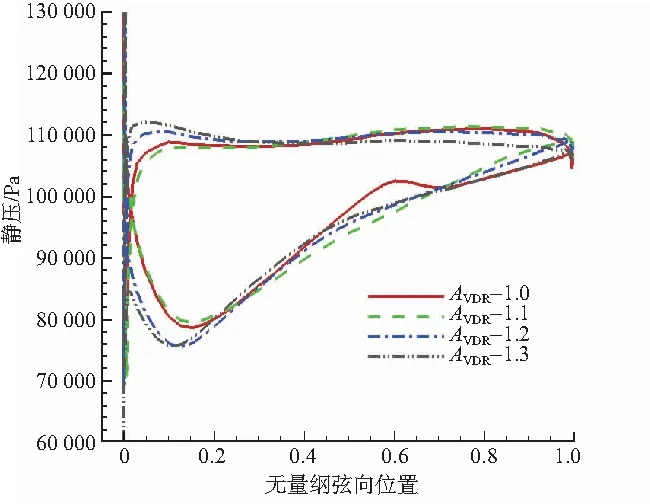
圖13 0°攻角高亞音轉子葉柵葉片表面壓力分布

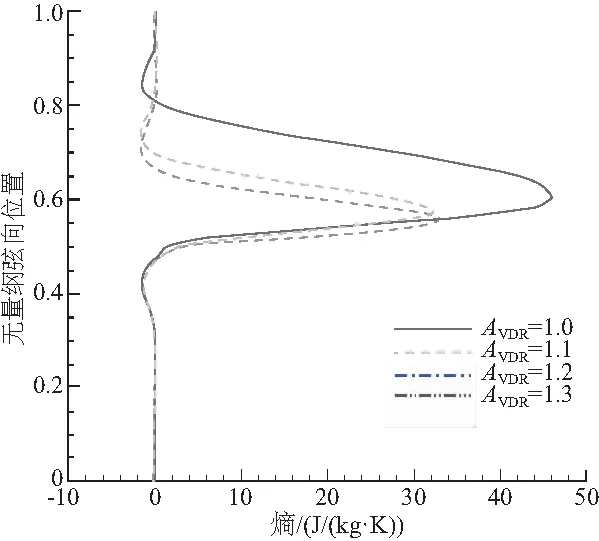
圖14 0°攻角高亞音轉子葉柵尾緣后10%軸向弦長熵沿切向分布

4 結語

本文采用數值模擬方法，研究密流比對于典型超音、高亞音轉子葉柵氣動性能影響規律，得出以下結論:

1)軸流壓氣機轉子葉片通道10%、50%葉高處符合回轉面二維流動；90%葉高處流動由于較強的三維性，可能形成音速喉道，造成三維流動與回轉面二維流較大差別；但在回轉面葉型設計時，不會產生喉道。因此對于軸流壓氣機轉子三維葉片在10%～90%葉高范圍內采用二維設計方法是可行的。

2)對于超音葉柵，密流比增加，總壓比和效率均增大，結尾正激波前移，耐反壓能力下降；對于高亞音轉子葉柵，氣流轉角增大，低損失氣流角及范圍增大。